2022 年 43 巻 4 号 p. 106-124
2022 年 43 巻 4 号 p. 106-124
眼鏡レンズの幾何光学に関しては、様々な教科書1)2)3)が出版されている。本稿では、眼鏡レンズを製造してきた立場からの情報を追加し、これら教科書の再編を行った。眼鏡レンズは他の視力補正レンズと異なり、レンズ周辺部の光学特性を考慮しなければならない。このため、実際のレンズ設計では軸外収差理論や眼球光学系の情報が必要になってくるが、本稿では扱っていない。レンズ幾何光学の入門知識として気楽に読んでいただければ幸いである。
Various textbooks1) 2) 3) have been published on the geometrical optics of spectacle lenses. In this paper, we have added information from the standpoint of eyeglass lens manufacturers and reorganized these textbooks. Spectacle lenses differ from other vision correction lenses in that the optical characteristics of the lens periphery must be considered. For this reason, off-axis aberration theory and information on the eyeball optical system are required for actual lens design, but this paper does not deal with them. We hope that you will enjoy reading it as an introductory knowledge of lens geometric optics.
1枚の眼鏡レンズは,レンズの前面と後面との2つの屈折面により構成される。実際に光が屈折するのは,空気とレンズ材料の境界面であるレンズ前面と後面の2箇所である。レンズ全体の屈折効果は,レンズ前面での屈折効果と,レンズ後面での屈折効果の合成となる。レンズ面での屈折効果を面屈折力,レンズ全体の屈折効果をレンズ屈折力と呼ぶ(図1)。

面屈折力とレンズ屈折力
なお,レンズの形は様々なものが考えられるが,本稿では図1に示すようなメニスカス形状を前提に説明を行う。
また,以降の説明では図2に示す直交座標系を使用する。物点から眼球に向かう方向をZ軸のプラス方向,上方向をY軸のプラス方向,眼球から物点を見た時の右手方向をX軸のプラスとする。眼鏡処方を考える場合は,観察者から眼球を見た時の右手方向がX軸のプラスと定義され,本稿の定義とは逆になるので注意が必要である。
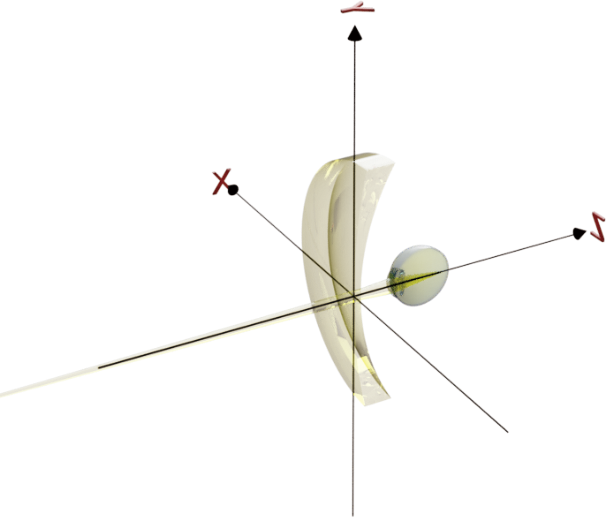
直交座標の定義
レンズ面の基本的な形状は球面である。
図3に示すように,Z軸上の点Q(0,0,R)を中心とする半径Rの球面を考える。球面上の任意の点P(x,y,z)は以下の関係が有る。

球面形状
ここで,
球面形状を計算するのに通常は(式1)で十分であるが,円の半径が極端に大きく平面に近づいた場合には,計算機でエラーになる場合がある。この場合の対応として,球面の半径に代わって曲率C(=1/R)を用い,次のように置き換えることができる。
なお,各数値の単位はメートルを基準とするが,実質的にはミリメートルが用いられることが多い。
1.1.2 球面の面屈折力とレンズの屈折屈折面の面屈折力PSは以下の式で計算できる。
ここで,n1・n2は屈折面の両側の屈折率,Rは屈折面の半径である。Rの単位がメートルの場合,PSの単位は〔m-1〕であるが,慣例的にD(ディオプトリ)と表示する。
図4は前面の半径がR1,後面の半径がR2,中心厚tの球面レンズの断面図である。レンズの材料の屈折率はn2で,レンズの前後は屈折率n1とする。レンズ前面の面屈折力PS1及びレンズ後面の面屈折力PS2は式3から

球面レンズの屈折力
レンズの中心厚tが充分薄い場合は,レンズの屈折力Plensは2つの面屈折力の和で表わされる。
眼鏡レンズの中心厚は最も薄いものでも1 mm程度有り,実際の設計の現場では無視できない厚さである。レンズの中心厚を考慮したレンズ屈折力の計算は,様々な文献で紹介されているので割愛する。
一般的な光学のテキストは,屈折面の間に主点を想定した主点屈折力を基準としている。主点の位置はレンズの形状により異なるため,眼鏡レンズの場合の基準点としては使いにくい。このため,眼鏡レンズでは,レンズ前面位置または後面位置を基準にした頂点屈折力(vertex power)を用いるのが一般的である(図5)。

主点屈折力と頂点屈折力
後面頂点からの後側焦点までの距離Fvbの逆数を後面頂点屈折力(Back vertex power)と呼び,眼鏡レンズの屈折力として一般的に用いられる。中心厚を考慮した後面頂点屈折力Pvbは以下の式で計算できる。
ここで,PS1,PS2は式5で使用した面屈折力,tはレンズの中心厚,n2はレンズの屈折率である。
乱視用レンズ(トーリックレンズ)を製造するために,2つの主経線の曲率半径が異なるトロイダル面が用いられて来た。トロイダル面は,有る半径の母円をその中心を通らない軸で回転させたときにできる面で,図6に示すようにタイヤ型と樽型が有る。

トロイダル面
タイヤ型は半径rの円を半径Rの軸で回転させたもの,樽型は半径Rの円を半径rの軸で回転させたものである。どちらも主経線上での曲率半径は同じなので,レンズに用いた場合はレンズ中心部付近では同じ乱視屈折力レンズとなるが,レンズ周辺部での形状は若干異なる。レンズを加工する機械の構造上,タイヤ型の方が作りやすいので,眼鏡レンズの乱視面としてはタイヤ型トロイダル面が一般的である。
タイヤ型トロイダル面の形状上は以下の式で表される。
樽型の場合はR⇔r及びx⇔yの入れ替えを行った式になるが,x=0またはy=0の経線上以外では,タイヤ型の式とは同じにはならない。
トロイダル面は機械式加工機を使うためには便利な式であるが,最近ではNC加工機の普及により,計算がしやすいバイコーニック(Biconic)面を使う場合が多い。Biconicはcx=1/R,cy=1/rと置き換えて,以下の式で表される。
上式はx,yに対して対象なので,トロイダル面のように軸の取り方で面が変わるということが起きない。また,後述する非トロイダル面へも容易に拡張することができ,便利である。
1.2.2 トーリックレンズによる結像トロイダル面およびバイコーニック面は2つの主経線を持つため,各経線方向の光線の収束位置が異なり,各収束位置では光は点に集まらず線として集光する。これを焦線と呼ぶ。2つの焦線の間に最小錯乱円と呼ぶ最も集光する位置が存在する(図7)。トロイダル面およびバイコーニック面を有するトーリックレンズも,基本的に2つの経線方向で最大屈折力と最小屈折力が決まる。

トーリックレンズの屈折
トーリックレンズの2つの主経線の間の中間屈折力は以下の式で計算できる。
ここで,PH,PVはトーリックレンズの2つの主経線屈折力で,図8では水平方向をPH,垂直方向をPVとしている。θはPHからの角度である。
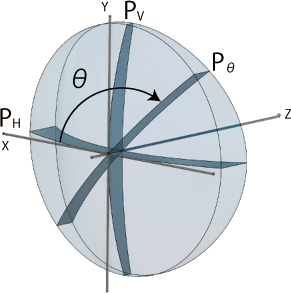
トーリックレンズの任意方向の屈折力
なお,前述したようにトロイダル面の表現が2通り有ることから,式10は眼鏡レンズの光学中心付近の狭い範囲のみで使用できる近似式である。特に,プリズム屈折力が入っている場所では式10は成立しない。
また,一般的に処方箋に記載される乱視軸は,観察者側から見たとき,主経線(PHまたはPV)が水平方向からどれくらい傾いているかを表すもので,上記のθとは異なる。
1.2.4 乱視レンズの度数表記,度数転換トーリックレンズは2つの主経線屈折力を持つが,眼鏡の慣例として球面屈折力と乱視屈折力という表現をする。球面屈折力は2つの主経線屈折力のどちらか一方の屈折力で,乱視屈折力は2つの主経線屈折力の差で表される。どちらの主経線屈折力を球面屈折力とするかは国によって異なるが,日本でのレンズの表記は基本的に絶対値の小さい方の屈折力を球面屈折力とし,表1の様になる。
| 球面度数の符号 | 乱視度数の符号 | |
|---|---|---|
| 遠視性乱視 | + | + |
| 近視性乱視 | - | - |
| 混合性乱視 | + | - |
欧州では全ての範囲で乱視屈折力が(+)となるように球面屈折力が定義される。すなわち,よりマイナス側の屈折力を球面屈折力と呼ぶ。
また,米国では全ての範囲で乱視屈折力が(-)となるように球面屈折力が選ばれている。眼鏡に関するISO規格のうち,レンズ製造に関する情報処理の分野ではマイナス乱視表記が基準となってきている。
球面屈折力の方向を乱視軸の方向とすることは,全ての国で共通の認識である。このため,日本,欧米で乱視度数の符号を変えるときには乱視軸の方向も考慮して度数変換する必要がある。
1.2.5 トーリックレンズの合成2枚の乱視レンズの組み合わせや,眼鏡レンズの乱視屈折力と眼球の乱視屈折力との組み合わせの際,屈折力の合成を考慮する必要がある。球面屈折力S1・乱視屈折力C1・乱視軸A1のレンズと,球面屈折力S2・乱視屈折力C2・乱視軸A2の2枚のレンズを重ねたとき,合成された屈折力Stotal,Ctotal,Atotalは以下のようになる。
眼鏡レンズで2枚のトーリックレンズを重ねて使用することは殆ど無いが,式11は処方に対してレンズが傾いて枠入れされた場合等の残余乱視の影響を考察するのに役立つ。
1.3 非球面,非トロイダル面 1.3.1 非球面・非トロイダル面の形状眼鏡でいう非球面レンズとは,一般的にZ軸(光軸)に対して回転対象の形状を持つものを言う。このためZ軸を通る任意の断面で以下の形状を定義し,Z軸周りに回転して非球面形状を作製する(図9)。
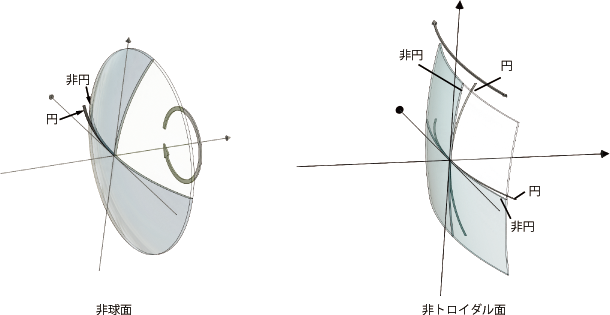
非球面と非トロイダル面
式12の第1項は,式1と同じ球面の式である。式12の第2項は非球面項で,一般的にはiの値として2,4,6,8,12等の偶数次項が用いられる。偶数次が用いられるのは,0点での面の繋がりを滑らかにするためであるが,最近ではコマ収差を加えて焦点深度を稼ぐため,3次の項を付加した設計も行われている。
眼鏡用非球面レンズとしては,前面が非球面のもの,後面が非球面のもの,両面とも非球面のものが製品化されている。非球面加工を行うにはNC加工機(Numerical Control machine)が必要である。
非トロイダル面は,2つの主経線のどちらか一方,または両方を式12に倣って非円形としたものである。トロイダル面自体がZ軸に対して回転対象では無いため,非円形を使った非トロイダル面もNC加工が必須となっている。バイコーニック面も同様である。
1.3.2 非球面・非トロイダル面による結像式12の非球面項はレンズ周縁部での焦点位置をコントロールするように決められる。具体的には,球面レンズまたはトーリックレンズで光線追跡を行い,焦点位置のズレや収差の出方を見ながら,所定の光学特性になるように補正を行う。一般的に,球面レンズは周縁部で過矯正になりやすいので,屈折力が一定になるように補正を行う。また,周縁部での非点収差などを最小にすることなどが行われている。
1.4 自由曲面 1.4.1 累進屈折力レンズの形状と光学特性累進屈折力レンズの屈折面は,遠くを見るための屈折力と近くを見るための屈折力を有するために,レンズ1面の中で曲率半径が滑らかに変化するような形状をしている。累進面を定義する方法は,各レンズメーカー固有の技術で公開されていないが,ISO規格の中では双3次スプライン曲面を累進面の加工に使用すると紹介されている。
双3次スプライン曲面は,図10のように曲面を等間隔に分割し,各格子を双3次曲面で表したもので,双3次式は以下のように表される。

スプライン曲面
ここで,xyは各格子点の左下を基準とした格子内の座標を表す。
式13では,1つの格子に対して,16個の係数Aijが存在する。また,実際の加工では1 mmピッチで格子点の座標(X,Y,Z)を与えるので,例えば外径80 mmのレンズの場合,格子は80×80=6,400個存在する。各曲面が滑らかにつながる様,各格子の境界上で2階微分まで連続という条件を付加し16×6,400=102,400個の係数Aijを使い自由曲面を表現する。
平面プリズムは,平面形状の2つの屈折面を互いに傾けて置いたものである。2つの屈折面の交線(稜線)に垂直な断面を主断面,主断面における交点を頂点,面のなす角を頂角,厚い方の端部を基底と呼ぶ(図11)。

プリズム
プリズムの屈折率をn1,プリズムの外側の屈折率をn0とすると,頂角αのプリズムでは入射光線と出射光線が偏角δをなす。2つの屈折面ではスネルの法則に従い,以下の屈折が生じている。
式14-1~4を解けば,偏角δは入射角θ1と頂角αの関数として表すことができる。眼鏡レンズでは偏角の代わりにプリズム屈折力PZを使うが,これは入射光線が100 cm(=1 m)進んだとき出射光線が何センチメートル変位するかを表したもので,以下で表される。
プリズムの単位はプリズムディオプトリ(Δ=cm/m)で表す。眼鏡レンズで扱うプリズムは10(Δ)程度であり,式15から逆算するとtanδ=δと近似できるくらいの小さい角度である。同様に式14-1,-2においてもsinθ=θと近似できるので,式14-1,-2は以下のように簡単になる。
式14-3~5により,
プリズムの大きさは式15により,プリズム屈折力で表される。光線はプリズムの基底方向へ曲げられるので「プリズムの基底方向」をプリズムの方向として指定する。基底方向は,眼鏡レンズの物体方向から見た時の右手側を0度とするタボ(TABO)角度目盛システムを用いて,0度から360度で指定する。このほか,水平方向プリズムに対しては鼻側をIN,耳側をOUT,垂直方向プリズムでは上側をUP,下側をDOWNと呼ぶ場合も有る(図12)。

TABO式
プリズム屈折力の大きさは式14で説明したように光線の入射角θ1とプリズム頂角αの関数となる。このことは,入射光線の入れ方によってプリズムの測定値が変化するということを表している。一般的に,入射角と出射角が等しくなる時,偏角δは最小になることが証明されており,これを最小偏角という(図13)。

最小偏角
なお,眼鏡レンズでは「レンズ後面をレンズメータのレンズ受けに当てて」プリズムを測定することになっている。このため,レンズメータでのプリズム測定値は最小偏角の測定とはなっていない。
2.2 眼鏡レンズのプリズム作用度付きレンズは,レンズの中心から外周部に掛けて,微小なプリズムが連結したものと考えることができる(図14)。レンズ中心部以外でのプリズム屈折力は,レンズの焦点屈折力(度数)から計算できる。

度付きレンズのプリズム効果
球面レンズを使って,レンズの焦点屈折力とプリズム屈折力の関係を見ていく。
図15のように,収差の無い理想的なレンズを考える。レンズの後面頂点屈折力(度数)はD(ディオプトリ)で,焦点距離をf(m)とする。レンズの光軸からL(cm)離れた位置を通過する光線は,レンズにより屈折され,焦点Fを通過する。図ではレンズの前面と後面とで2度屈折するため計算が難しくなるが,後面頂点の位置で1度だけ屈折すると見なすと,以下のような近似式が成り立つ。

焦点屈折力とプリズム屈折力
また,式15より
屈折力D(dptr)のレンズ中心からL(cm)離れた位置でのプリズム屈折力PZ(Δ)はL×Dで近似計算できる。プリズムの方向は,Dがプラスならばレンズの中心に向かう方向,Dがマイナスならばレンズの外周に向かう方向がプリズム基底方向となる。
レンズの中心部で0(Δ)のレンズでも,L(cm)離れたところでL×D(Δ)のプリズム屈折力が得られるので,眼鏡フレームに枠入れする際に偏心加工を行って所定のプリズム処方に対応することが有る。但し,偏心加工ができるのは屈折面が球面またはトロイダル面の場合だけで,非球面レンズの場合は偏心により光学性能が著しく変化するため,枠入れ時の偏心加工はできない。
2.2.2 乱視レンズのプリズム屈折力乱視レンズは2つの主経線屈折力を持つので,その各々の屈折力にプレンティスの式を適用し2つのプリズムを求めた後,合成する。
図16(a)の様に,球面屈折力S(D),乱視屈折力C(D),乱視軸α(度)のレンズの点P(x,y)での位置のプリズムを求める。まず,図16(b)の様な乱視軸が水平なS-C座標系で,点Pに対応する点Q(u,v)の位置を求め,プリズムPsとPcを計算した後,ベクトル合成でプリズム屈折力Pz及び基底方向を求める。ここで求めた基底方向はS-C座標系での値なので,元のx-y座標系の基底方向に変換するためα度回転して求める。

乱視レンズのプリズム計算
一般的に,点Pでのプリズム屈折力Pのx成分,y成分は以下のように計算できる。
ここで式20-4のωは,Px,Pyの符号によって0度,90度,180度,270度の値を取る。
日本においては,レンズの後面と角膜までの距離を12 mmとするのが慣例である。また,眼球の回旋中心はレンズ後面から25 mmとしている(図17)。

眼鏡レンズの配置
最近の眼科機器の発達により,眼球のサイズや光学的な配置が徐々に解明されつつあり,将来上記の数値の見直しもあると予想される。また,これまでの眼鏡レンズ設計では水晶体の形状や,網膜の形状などは厳密には議論されて来なかったが,将来的にはこれらも含めた総合的な光学系の中でレンズ性能の評価が行われていくと考えられる。
3.2 眼の構造と生理光学的特性 3.2.1 眼鏡レンズの非点収差分布と平均度数分布通常の幾何光学のテキストには必ず出てくるザイデルの5収差であるが,眼鏡レンズでは基礎知識として知ることは重要であるが,実際の光学設計の現場では重要視されない。なぜなら,ザイデルの5収差は,屈折面が球面の場合で,光軸付近での収差を考察しているが,眼鏡レンズは光軸外での光学性能も重要だからである。さらには,レンズにプリズムが入っていて光軸が存在しないものや,眼鏡フレームに枠入れする際に眼球に対してレンズが傾いて置かれるもの,自由曲面により屈折面が球面とは懸け離れているもの,などにより実際には図18に示すように,光軸外での集光分布と集光の中心(最小錯乱円)が網膜からどれくらいずれるかを評価することになる。

眼鏡レンズの収差
屈折面が複雑になるほど集光分布は偏りが大きくなるが,レンズ評価の代表値として最大屈折力と最小屈折力が用いられ,両者の差を「非点収差」,両者の平均を「平均度数」としてレンズの光学性能評価マップを作製する(図19)。
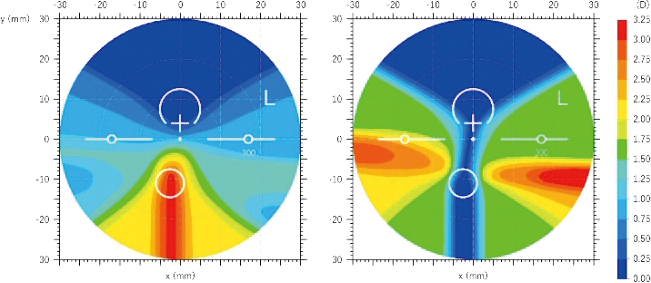
平均度数マップ(左)と非点収差マップ(右)
レンズの材料特性から生じる収差の一つが色収差である。図20に示すように,色収差には軸上の色収差と倍率の色収差が有り,それぞれ以下の式で表される。

色収差
ここで,Dはレンズの屈折力(dptr)で,νeはレンズ基材のアッベ数で以下のように定義される。
なお,ne,nF′,nC′はそれぞれ,水銀e線(緑)546.07 nm,カドミウムF′線(青)479.99 nm,カドミウムC′線(赤)643.85 nmに対する屈折率である。また,式21-2の最終項はプリズムをプレンティスの式で置き換えたもので,レンズ中心からの距離Lが大きくなると,色収差も大きくなることが分かる。
軸上の色収差は,光軸上での各波長光線の焦点位置ずれとなる現象である。カメラのように細かくピントを合わせる必要がある場合には象の品質に影響が有るが,眼鏡レンズの場合には眼球の補正効果により問題視されていない。一方の倍率の色収差は,軸外のプリズム効果によって発生するもので眼球での補正は効かない。このため,アッベ数の小さな材料で強度数の眼鏡レンズを作製した場合,見える像の縁で色がにじむと訴える人もいる。過去の経験で,Cmagが0.2を超えると色のにじみを感じるという人が現れる。
3.3 非点収差の削減 3.3.1 チェルニングの楕円球面またはトロイダル面を使ったレンズの場合,面を定義するパラメータは曲率半径しか無いため,どのような曲率半径を用いるかによってレンズの光学性能が大きく左右される。
図21はチェルニングの楕円と呼ばれるもので,非点収差を最小にするための眼鏡レンズの屈折力(レンズ度数)とレンズ前面の屈折力(ベースカーブ)との関係を表す。例えば-10(D)のレンズの場合,ベースカーブ値2.7(D)のOstwalt解(青)と,ベースカーブ値15.9(D)のWollaston解(緑)の2つのベースカーブ値が,最も収差の少ない球面レンズを提供できる(但し,図21は屈折率1.50,物体距離無限大として解いたもので,条件が異なれば解も異なる)。
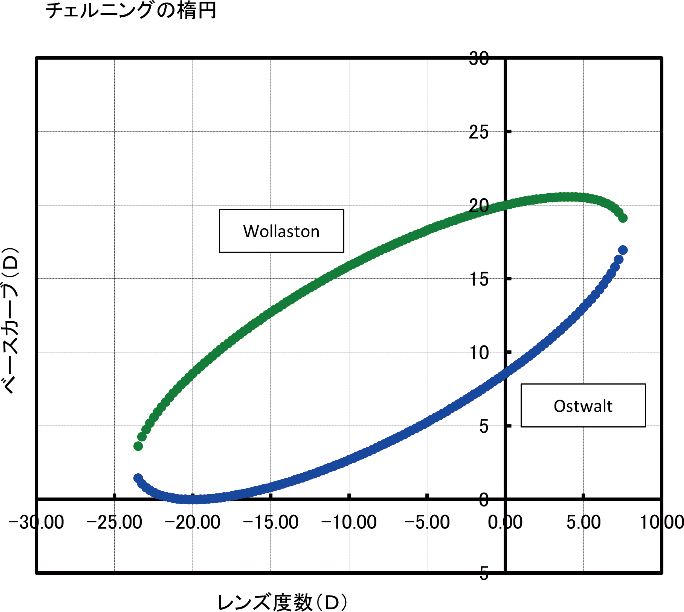
チェルニングの楕円
一般的には,ベースカーブ値が小さいとレンズ面が平面に近くなり,見栄えと枠入れ加工がしやすいので,Ostwalt解の方を使用する。しかしながら,現在市場に出ている球面レンズの多くが,Ostwalt解よりも小さいベースカーブ値を採用し,非点収差の影響が出ない範囲で,薄く見栄えの良いレンズが製造されている。
また,最近では非球面を使い非点収差補正を行った非球面レンズが主流であり,この場合はさらに小さなベースカーブ値を採用しており,チェルニングの楕円理論からは大きくずれている(図22)。

ベースカーブ設定例
眼鏡レンズは光軸から外れたところでの光学性能が問題になってくるので,図23のように眼球を回旋中心で回転させたときの光線を計算し,屈折力を求める。光軸(Z軸)に対して回転対象形状の球面・非球面レンズでは,レンズの子午線に沿った断面方向(Tangential)とそれに垂直な断面方向(Sagital)の屈折力が最大値または最小値を取るので,代表値として扱う。

眼鏡レンズの光学性能評価
図22のベースカーブ設定を用い,Ostwaltレンズ,球面レンズ,非球面レンズの屈折力変化を比較する。レンズの屈折力はS-6.00D,レンズ中心厚2.0 mm,屈折率1.50を用いて計算した。
図24はOstwaltの球面レンズで
(a)Tangential/Sagital方向屈折力
(b)非点収差/平均屈折力
(c)レンズ断面形状
を表す。(b)の非点収差はSagital屈折力からTangential屈折力を引いた差分,平均屈折力はSagital屈折力とTangential屈折力の平均値である。

Ostwaltレンズの光学性能
図24のOstwaltレンズでは,(b)非点収差の値が視角0°~25°の範囲でほぼゼロとなっており,レンズの中央部付近でのボケが少ないと考えられる。しかしながら,屈折力はレンズの外周部に向かうにつれプラス側にシフトしており,視角30°以上では0.25D以上の弱矯正になっている。
図25は,一般的に市販されている球面レンズの例である。Ostwaltレンズにくらべ全体にマイナス側に屈折力がシフトしており,レンズ外周部では過矯正である。非点収差はOstwaltより多めになるが,平均屈折力はOstwaltより安定している。また,レンズ断面形状がフラットになって,40 mm位置でのレンズ厚みが減少している。

球面レンズの光学性能
図26は非球面レンズの例である。ベースカーブ値は市販の球面レンズより小さいため,非球面補正を行う前は図25より過矯正になる。図26では非球面により補正を加えているため,特に平均屈折力はレンズ全体で大きなずれはなくなっている。また,非点収差も改善され,レンズの厚さも薄くなっている。

非球面レンズの光学性能
累進屈折力レンズでは,遠用部と近用部で屈折力が異なるため,それぞれ異なる非球面で非点収差の補正を行う。また,累進屈折面が自由曲面で有るために発生する非点収差も存在する。一般的に,遠用部・近用部で大きな明瞭領域を確保すると,遠用部と近用部との境界では屈折面が急激に変化するため,収差が発生し,レンズを通してみた時の象のゆがみも大きくなる。
遠用部・近用部の球面領域をどのように設定するかは,累進レンズの見え方や掛け慣れやすさが大きく変わるため,各レンズメーカーのノウハウになっている。図27は遠用屈折力がS0.00Dで,近用の屈折力をS+1.00D/S+2.00D/S+3.00とした累進レンズマップである。
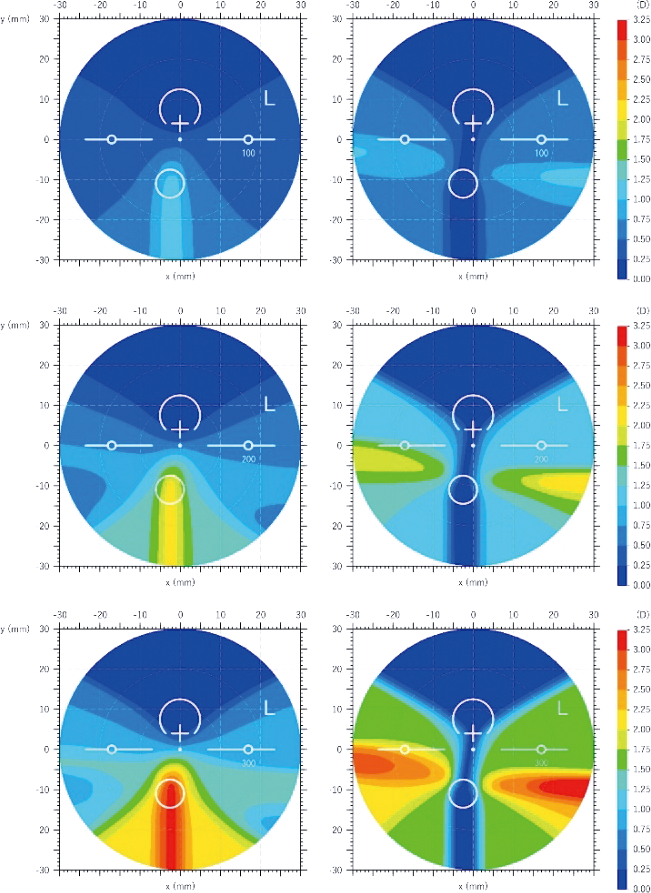
累進レンズの性能評価
眼鏡レンズを装用すると網膜像に変化が生じる。最も顕著なものは網膜像の大きさが変わることで,この変化は「眼鏡倍率(Spectacle Magnification)」と「相対眼鏡倍率(Relative Spectacle Magnification)」とで表現される。眼鏡による倍率は,光軸上に無い物体を見るための眼球回旋や,不同視による左右像のずれ,それの伴う眼精疲労などを生じる可能性がある。また,プラス度数のレンズでは,視野の空白部分を生じる。以下では,眼鏡倍率の表現とその影響について説明する。
4.1 眼鏡倍率(Spectacle Magnification)眼鏡倍率SMは以下のように定義されている。
図28(a)は,眼鏡補正前の網膜像の大きさを表す。目の入射瞳Eから距離qに有る大きさη0の物体を見た時,網膜上の大きさη1は

眼鏡倍率SM
図28(b)のように,眼前heの位置に屈折力Dのレンズを置いた場合,レンズの中心を通った光線は網膜位置で大きさη2の象となる。
式23と式24,式25から
ここで,tはレンズの中心厚,D1はレンズの前面屈折力(ベースカーブ),nはレンズの屈折率である。また,hveはレンズの後方頂点と目の入射瞳の距離,Dbはレンズの後方頂点屈折力である。
式29の(1-t D1/n)-1および(1-hev Db)-1はそれぞれ,シェープファクター(Shape factor),パワーファクター(Power factor)と呼ぶ。
式29のシェープファクターは,レンズの屈折力が同じ場合でも,レンズの中心厚とベースカーブによって倍率が変化することを示している。この原理を用いたサイズレンズについて後述する。
なお,眼鏡倍率は任意の主軸上に視線を固定した状態での,主軸近辺の象の倍率について表現している。視線を振ったときの角度の拡大縮小ではないことに注意したい。
4.2 瞳の位置と倍率眼鏡レンズを掛けることにより,瞳の位置と瞳径の大きさが変わる。図29は眼球の瞳Eから距離heの場所に屈折力Dのレンズを置いた時の,新しい瞳位置Enewを示す。瞳径の大きさも変化し瞳倍率Mは以下のように表される。

瞳の位置と倍率
ここで,結像公式1/l′-1/l=Dを式30に適用すると,
式33は,眼鏡レンズがプラス度数の場合は1より大きくなるので,式30から瞳径が拡大され,光束の量が増えることを示している。ただし,網膜像も同じ倍率だけ拡大されるため,網膜像の明るさが変化することは無い。
4.3 相対眼鏡倍率(Relative Spectacle Magnification)相対眼鏡倍率は,正視眼の網膜像サイズに対する,眼鏡補正眼の網膜像サイズの比で,以下のように定義される。
図28(a)及び式24に示した通り,網膜像の大きさは物体の視角ωと網膜までの距離eの積で表される。正視眼の眼球屈折力をFeとすると,網膜上に焦点が合っていると考えるとe=1/Feである。従って,式24は以下のように表される。
一方,屈折異常眼に眼球を掛けた状態の眼球と眼鏡レンズの総合屈折力をFtとする。上記正視眼と同じ物体を見ているとすると視角は同じωであり,網膜に焦点が合っているとすると,式35と同じく以下が成り立つ。
屈折異常の目の屈折力をFa,眼鏡レンズの屈折力をD,レンズ後面と目の前方主点までの距離をhpとすると
屈折異常が軸性によるものだけならば,目の屈折力は正常眼と同じでFa=Feである。
この場合,式38は次のようになる。
ここで,feは目の前側焦点距離でfe=-1/Feである。
hpは一般的に15~20 mmであり,眼球の屈折力が60Dの場合fe=-16.67 mmで,hpとfeは近い値である。もしレンズをhp=16.67に置いた場合RMS=1となり,正視眼と同じ網膜像サイズとなる。
(屈折性の屈折異常の場合)眼軸が正視眼と同じ場合には,屈折異常眼の屈折力Faと眼鏡の有効屈折力の和は,正視眼の屈折力Feと同じになる。
上式で,D/(1-hpD)は,眼球の前主点Pの位置でのレンズの有効屈折力である。式38に式40を代入すると
式41と式28で示したSMとの違いは,レンズと眼球の距離を入射瞳までの距離heで定義するか,目の前側主点までの距離hpで定義するかの違いだけである。この違いは約1.5 mmである。
相対眼鏡倍率は以下の理由であまり使われていない。
① 相対眼鏡倍率は軸性か屈折性かで結果が異なるが,屈折異常がどちらであるかは分かりにくい。
② 基準としている正視眼の定義は将来変わる可能性がある。また,左右不同視の場合には左右の相対的な比率が重要であり,正視眼に対する比率は重要ではない。
③ 相対眼鏡倍率は,網膜像のサイズによって定義されているが,網膜の受容体の分布や視神経の再編などによって,実際に見えるサイズは違ってくる。

相対眼鏡倍率のパラメータ
眼鏡レンズを装用すると,遠点と近点が変化し,調節負荷にも影響が生じる。遠方視力を補正すると,遠点は無限遠に移動する(実際には5~6 m先)。このとき,近点は図31のように変化する。

眼鏡レンズによる近点移動
屈折方程式から
式44は,角膜頂点から眼鏡レンズを通して見た物体までの距離の逆数,すなわち物体に焦点を合わせるために必要な屈折力(眼球屈折力とレンズ屈折力全体の)である。
一方,眼鏡レンズの屈折力Dは遠点を無限遠に配置するための屈折力で,眼鏡レンズの角膜頂点位置での有効屈折力D0は以下の通りである。
遠点からW′までの調節は眼球が行うので,眼球の調節力をA(W)とすると,
眼鏡倍率(SM)及び相対眼鏡倍率(RSM)は光軸上での倍率を与えるものである。眼鏡レンズの拡大効果は軸外の物体を見るときの目を回旋角に影響し,これを回転倍率(Rotational Magnification)と呼ぶ。
式47は眼鏡倍率SMの式と似ているが,SMは眼球の入射瞳を基準に定義していたのに対し,RMは眼球の回旋中心を基準に定義する(図32)。

回転倍率のパラメータ
(a)レンズが無い時の目の回旋角
(b)レンズを通して見た時の目の回旋角
式26,27と同じように解くと
図33にプラス及びマイナスの眼鏡レンズを掛けた時の視野(Field-of-view)を示す。見かけの視野は,眼の回旋中心Cを中心とした最大眼球回旋角θ′maxで以下のようになる。

実際の視野と見掛けの視野
DSは眼鏡レンズの有効径である。実際の視野θmaxは式47からθmax=θ′max/RMであり式48と式50を使うと以下のように表される。
遠方物体の場合は
式50と式52を比べると,レンズの屈折力Dがプラスの場合はθmax<θ′maxとなり,図33(a)のように暗点ができる。逆にDがマイナスの場合はθmax>θ′maxとなり,(b)の様に複視の領域が発生する。
これまでの説明では実際の視野に対するゆがみを無視しているため,角度が大きい場合は注意が必要である。
4.5.3 視界視界(Field-of-vision)は,光軸上に眼球が正視した状態での視野限界である。式50~52においてqc及びhcの代わりに,眼鏡倍率で使用した入射瞳を中心としたq及びheを使用する。
4.6 サイズレンズ眼鏡倍率SMの式29によると,レンズの倍率は,レンズの中心厚t,前面屈折力D1,屈折率nで決まるシェープファクターと,レンズから眼球の入射瞳までの距離hevとレンズの後面頂点屈折力Dbによって決まるパワーファクターとの積になっている。
パワーファクターの方は,レンズ屈折力がプラスだと像が大きくマイナスだと小さく見えることや,プラスのレンズを眼から離すと像が大きくマイナスレンズを眼から離すと小さくなるといった現象で体感ができる。一方,レンズの屈折力やレンズを置く位置が同じ(パワーファクターが同じ)でも,シェープファクターによって倍率を変えることができることを示している。
具体的な例として,後面頂点屈折力が0Dで,入射瞳からレンズまでの距離を15 mmとしたときの,シェープファクターと倍率を見ていく。
表2は具体的なサイズレンズの設計例を,通常レンズとの比較で示している。表中Aの標準レンズは屈折率1.50でS0.00Dのレンズで,前面屈折力が5D,中心厚2 mmである。このレンズの眼鏡倍率SMは1.007で,0.7%の拡大率である。一方,Aのサイズレンズでは前面屈折力が9.5D,中心厚6.0 mmとしている。前面の曲率半径が52.632 mmとなり加工できる限界であるため,中心厚を厚くして倍率を稼いでいる。このレンズの拡大率は4%である。左右眼で3%以上の拡大率差がある場合,両眼視に影響が出ると言われており,この標準レンズとサイズレンズとの組み合わせで,レンズ度数を変えずに拡大率差だけを補正することができる。
| A | B | C | D | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 標準 | サイズレンズ | 標準 | サイズレンズ | 標準 | サイズレンズ | 標準 | サイズレンズ | ||
| 後面頂点屈折力 | Db(D) | 0.00 | 0.00 | -4.00 | -4.00 | 0.00 | 0.00 | -4.00 | -4.00 |
| 入射瞳からレンズ後面までの距離 | he(mm) | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| 屈折率 | n | 1.50 | 1.50 | 1.50 | 1.50 | 1.74 | 1.74 | 1.74 | 1.74 |
| 前面屈折力 | D1(D) | 5.00 | 9.50 | 2.00 | 5.50 | 5.00 | 14.00 | 2.00 | 10.00 |
| 中心厚 | t(mm) | 2 | 6 | 2 | 9 | 2 | 4.8 | 2 | 5.8 |
| 前面曲率半径 | Rf(mm) | 100.000 | 52.632 | 250.000 | 90.909 | 148.000 | 52.857 | 370.000 | 74.000 |
| 後面曲率半径 | Rb(mm) | 99.333 | 50.632 | 83.259 | 51.612 | 147.149 | 50.816 | 123.239 | 51.587 |
| パワーファクター | PF | 1.000 | 1.000 | 0.943 | 0.943 | 1.000 | 1.000 | 0.943 | 0.943 |
| シェープファクター | SF | 1.007 | 1.040 | 1.003 | 1.034 | 1.006 | 1.040 | 1.002 | 1.034 |
| 眼鏡倍率 | SM | 1.007 | 1.040 | 0.946 | 0.976 | 1.006 | 1.040 | 0.946 | 0.976 |
| 拡大率 | SM-1(%) | 0.7 | 4.0 | -5.4 | -2.4 | 0.6 | 4.0 | -5.4 | -2.4 |
表2BはS-4.00Dの場合の例である。度付きレンズではパワーファクターの影響が大きくなるため,拡大率はマイナスとなる。サイズレンズは後面の曲率半径が51 mmで加工限界となるため,前面の屈折力を5.5Dまでしか大きくできない。このため,中心厚を9 mmとして倍率を上げているが,標準レンズとの倍率差は3%である。
図34に屈折率1.50の標準レンズとサイズレンズの形状の違いを表した。サイズレンズは凸面の出っ張りが大きく,レンズも厚く・重くなる。

屈折率1.50 サイズレンズ形状
屈折率1.50のレンズでは加工上の制限が多いため,屈折率1.74で同様の設計を行ったのが,表2のC,Dである。1.50素材と同じ曲率半径でも1.74素材では屈折力換算値が高いためシェープファクターを大きくできる。また,屈折率が高い分,レンズ中心厚も薄くできる。
図35は屈折率1.74素材での,標準レンズとサイズレンズの形状比較である。1.50素材に比べ,実用的な形状になっている。また,図36は実際に屈折率1.74 S0.00Dのサイズレンズを作製した例で,拡大率は3%である。通常のS0.00Dレンズに比べ,凸面の出っ張りが大きく,レンズの厚みも2倍以上になっているが,異様な形状というわけではない。

屈折率1.74 サイズレンズ形状

サイズレンズ試作例
図37に図36のサイズレンズの効果を示す。レンズ無しの画像(左)に対して,サイズレンズをカメラの前に置いて撮影すると,像が拡大しているのが判る。(右)の画像はサイズレンズを凹面が前面に来るようにひっくり返して置いたもので,拡大率の符号が反転し像が縮小する。

サイズレンズの効果
(左)レンズ無し (中央)サイズレンズ3% (右)サイズレンズを裏返して使用
以上は単焦点レンズで説明してきたが,累進レンズでも同様に作成できる。その場合は遠用部と近用部で屈折力及びレンズ厚が異なるので,倍率に違いが現れる。
眼鏡レンズの屈折力を決める最も基本的な手段は,検眼レンズを使った測定である。検眼時の前提条件として,検眼レンズの後面と装用者の角膜頂点の距離は12 mmで,第一眼位の視線に対して検眼レンズが垂直に置かれる。この距離やレンズの角度がずれてくると,検眼レンズの眼球に対する有効屈折力が変わってしまうので,検眼時には注意が必要である。近用屈折力測定時も同様である。また,検眼レンズは球面屈折力レンズと乱視屈折力レンズ,プリズムレンズ等を複数枚組み合わせて検眼枠にセットするが,この場合最も眼球に近いレンズの後面と,角膜頂点が12 mmとなるように調整する(図38)。

検眼レンズの位置と傾き
実際に眼鏡として使用する場合は,様々な形の眼鏡枠に入れることになる。眼鏡枠に入れる場合も,眼前12 mmの位置で,第一眼位の視線に対して垂直となるように眼鏡枠調整と加工調整を行うことが望ましい。このように枠入れされるレンズは,検眼時に使用した検眼レンズと同じ屈折力で作られたものを使用することで,予定された視力を得ることが可能となる。
しかしながら,最近の眼鏡枠はデザイン重視のものが多く,上記のような調整がしにくくなっている。このため,頂間距離12 mmを確保できない場合や,視線に対して垂直にレンズを配置できない場合があり,その場合には実行屈折力を計算し,必要屈折力でレンズを発注する。
5.3 頂点間距離(装用距離)の変化図39のように眼の遠点位置とレンズの焦点が合致するようなレンズの屈折力D(h)を考える。ここで,hはレンズ後面から角膜頂点間までの距離(角膜頂点間距離)で,Lはレンズの焦点距離,dは眼の遠点距離である。また,De=1/dは角膜平面における屈折異常(屈折補正)である。

頂間距離
角膜頂点間距離hが変化したときの影響を調べるために式53をhで微分すると,
また,頂間距離h1で完全補正のレンズD1(h)と,h2で完全補正のD2(h)を考える。
式56と式57とで,眼の屈折異常は変わりないので,dについては同じである。式56をdについて解いて,式57に代入すると
式58は検眼時にh1=12 mmで測定したレンズ度数D1に対し,h2=15 mmの位置にレンズを置いた場合の必要屈折力D2を求めることができ,例えばD1=-8DとするとD2=-8,197Dが必要屈折力である。このD1とD2の差は式55の結果とほぼ一致する。
5.4 レンズの傾斜眼鏡枠にレンズを入れるとき,視線とレンズが垂直にならない場合が生じる。
眼鏡枠を上から見た時に,枠の耳側が顔に近づくように回り込んでいるものがあり,この枠に合わせてレンズを枠入れすると,レンズが外側に開いたように傾く。これをそり角という(図40)。一般的なメタルフレームでは,枠入れ前にレンズが視線に垂直になるように枠を変形する作業を行うが,図のようなプラスッチックフレームやチタンフレームでは変形できないものがあり,この場合はそり角に合わせてレンズの屈折力を補正する必要が出てくる。

そり角
また,眼鏡枠を横から見たとき,枠の上部が前方に倒れ込むように傾いている。これを前傾角という(図41)。眼鏡枠のテンプル部分に対して,レンズを入れるリム部分は10°程傾けて作られていることが多い。これは人の常用視線が水平より10°下がっており,これに合わせているという説がある。しかしながら,人の顔は千差万別で,眼鏡枠を支える鼻と耳の位置関係も人によりさまざまであり,テンプルが水平になるとは限らない。眼鏡レンズを補正するために必要な角度は,装用者が眼鏡を装用した状態での前傾角であり,個人個人の顔に合わせた測定が必要である。

前傾角
このように,眼鏡枠に入れる際には,第一眼位の視線に対してレンズが傾いているのが一般的であり,レンズ屈折力の補正が必要となる。レンズの傾きの影響についてはマーチンの式が有名である。
ここで,Dはレンズの後面頂点屈折力,θはレンズの傾き角,nはレンズの屈折率である。
Dtはレンズの傾きが生じている方向を含む断面(タンジェンシャル面)での屈折力,Dsはそれに直交する断面(サジタル面)での屈折力である。つまり,そり角の場合は水平断面でレンズの傾きが起きているのでDtは水平方向の屈折力であり,前傾角の場合は垂直断面で起きているのでDtは垂直方向の屈折力である。
式59,60は2つの主経線方向の屈折力なので,その差は乱視屈折力となる。
また,式12で説明したように,プリズム屈折力は入射光線の入射角に依存して変化するので,レンズが傾いて枠入れされる際には視線のズレを考慮してプリズム補正も行う必要がある。特にスポーツ用サングラスフレームのように,耳側に大きく回り込んだラップアラウンドタイプのフレームでは,レンズ屈折力がゼロでも視線のズレによる空間違和感が生じることがあり,視線補正対応のレンズを選択する必要が出てくる(図42)。

レンズ傾きによる視線ズレ
頂間距離,そり角,前傾角については,レンズメーカーで屈折力補正,プリズム補正を行っており,インディビデュアルレンズとして販売されている。なお,これらの補正はレンズのフィッティングポイント付近の極一部の領域の理論であり,眼鏡レンズ全体に対しては明確な理論は無い。各メーカーは光線追跡を行うことで屈折力の過不足を計算し,補正を行っている。
利益相反公表基準に該当なし