大規模な生命情報データの表現方法として、サンプルを行、計測した各要素を列とする行列形式は典型的な表現方法である。またこの行列データから相関関係や依存関係にある列のペアを検出する解析は、一般的なデータ解析手法であるといえる。この相関関係や依存関係を定量化する手法として、相関係数や相互情報量といった指標がよく利用されるが、これらの指標は擬似相関や偽陽性を多く検出する危険があることが知られている。近年では、このような偽陽性を防ぐための手法として生成モデルに基づくアプローチが利用されており、特にデータのとる値が離散(カテゴリカル)である場合は逆イジング法と呼ばれる。本総説では、この逆イジング法のモデルとパラメータの学習方法、およびタンパク質構造解析を中心とした生命情報データ解析への応用例について紹介し、今後の展開について議論する。
高速シーケンス技術を始めとする計測技術の進歩によって、多数のサンプルから多様なオミクスデータを取得する研究が様々な分野で行われている。これらの大規模データを表現する方法として、サンプルを行、計測した各要素を列とする行列形式はデータの自然な表現方法であり、一般的に広く用いられている。たとえばオーソログテーブルは、生物種を行、オーソログを列とした行列データとして表現されている。このような行列データ解析において、相関関係・依存関係にある独立ではない列のペアを検出する解析は、典型的なデータ解析手法である。オーソログテーブルの場合、相関関係・依存関係にあるオーソログペアの検出解析は系統プロファイル法と呼ばれ、機能未知のオーソログの機能推定やタンパク質相互作用推定などに利用されている[1, 2]。たとえば図1Aのようなケースでは、オーソログBとオーソログDが各生物種において全く同一の出現パターンを示しており独立ではないため、機能的に関係する可能性が高いと見積もられる。
この相関関係・依存関係を定量化する方法として、相関係数や相互情報量といった指標が良く用いられる。これらの指標は簡単に計算することができるという長所がある一方、対象とする列のペアのデータだけから計算される「局所的」な指標であるため、擬似相関や偽陽性を多く検出する危険があることが知られている。たとえば図1Bのようなケースにおいて、AとBおよびAとCが相関関係にある時、本来関係のないBとCの間でも高い相関係数が得られるという問題が生じる。そのため近年では、このような偽陽性を防ぐための手法として、全ての列の情報を同時に考慮したもとで、2つの列間の依存関係を定量化する「大域的」な指標が提案されている。この方法では、まず2つの列間の依存関係の強さを意味するパラメータを考え、そのパラメータを全ての列のペア分含んだ、サンプルデータの生成モデルを考える。そして機械学習を用いてデータからそのパラメータを学習し、その学習されたパラメータを列のペア間の依存関係の指標として捉える。

(A)系統プロファイル法の模式図。行は生物種を表し、列がオーソログを表す。
(B) 擬似相関の模式図。丸に囲われたアルファベットは要素、赤い実線は相関関係があるペア、黒い点線は擬似相関が検出されたペアをそれぞれ表す。
データの取る値が連続である場合には、その生成モデルはGaussian graphical modelなどで表現可能であり、生命情報データ解析においても遺伝子発現ネットワーク解析やメタゲノムデータの情報解析などに利用されている[3]。一方データの取る値が離散(カテゴリカル)である場合、その生成モデルはイジングモデル(データの取る値が二値の場合)やポッツモデル(データの取る値が多値の場合)として定式化される。この時、本総説では、このデータの値が離散(カテゴリカル)である場合のパラメータ学習問題を逆イジング法と呼ぶ。逆イジング法は、2006年にE. Schneidmanらによって神経活動データの解析で利用されて以来、生命情報データ解析で広く利用されてきた[4]。特にタンパク質の立体構造予測・相互作用予測においては必要不可欠の技術となっており、様々な応用研究が展開されている。本総説では、逆イジング法の基本モデルとその学習方法、そして生命情報解析における広い応用例を紹介し、今後の展開について議論する。
まず逆イジング法のモデルを簡単に紹介する。サンプル数をN、要素数をLとしたN×Lの行列データDを考える。ここで、Di,jはi行j列目のデータを意味し、Q個の離散値のうちいずれかの値をとるものとする。この時、列iにおいて要素xが現れる相対頻度をfi(x)、列iと列jにおいて要素xと要素yが共起して現れる相対頻度をfi,j(x,y)と定義すると、これらの値は次の式で計算できる。
ただしxおよびyはQ個の離散値のうちのいずれかの値とし、またδ(Dn,i,x)はDn,iとxが等しい時のみ1を返し、そうでない時には0を返す関数とする。あるサンプル(x1,…,xL)について、そのサンプルを生成する生成確率P(x1,…,xL)を考える。この時逆イジング法では、その同時確率分布が次の等式制約を満たすものとして確率モデルを与える。
ここでPi(x)およびPi,j(x,y)は、先の同時確率分布の列iおよび列iと列jについての周辺化確率である。任意のxおよびyに対してこの等式制約を満たすことを考えると、全ての事象の確率の和が1になる必要から、実質的な条件式の数は
ここでΩは考えうる全てのサンプルの集合とする。このような確率分布の定義方法は最大エントロピー法と呼ばれる[5]。本問題は等式制約付き最適化問題であることから、ラグランジュの未定乗数法で解くことが出来るため、サンプル(x1,…,xL)の生成確率P(x1,…,xL)はそのラグランジュ乗数hi(x)およびJi,j(x,y)を用いて次の形式で書くことができる。
この時、Ji,j(x,y)の値が大きいほど、列iと列jの間のxとyは依存関係にあることを意味している。またZは規格化定数であり、考えうる全てのサンプルについてその出現確率を足し合わせると1になることを保証するものである(分配関数とも呼ばれる)。この時、hi(x)およびJi,j(x,y)の値を求めることが本モデルのパラメータ推定問題となる。このように導出したモデルは、統計力学におけるイジングモデル(Q=2)またはポッツモデル(Q>2)と同一のモデルとなる。また、変数が離散値を取り、かつ全ての変数間が隣接しているとしてモデル化したマルコフ確率場(MRF)とも同一のモデルである。特にイジングモデルの時は、全ての変数間が隣接しているボルツマンマシンとみなすこともできる。
ここで解析的にそのパラメータを計算しようとすると、規格化定数Zを計算する必要が生じる。しかしながら、Zを厳密に計算するためには取りうるデータのQL個の組み合わせを全て考慮する必要がある。よってLが大きい時には、その組み合わせ数が膨大になり厳密な計算を行うことができない。それゆえ、最尤推定などに基づく様々な近似的パラメータ学習方法がこれまでに提案されてきた。ただし、学習すべきパラメータが大変多いため、尤度をそのまま最大化するとデータにオーバーフィットする危険性がある。そのため、L1ノルムやL2ノルムといった正則化項を加えた上でパラメータ推定を行い、オーバーフィットを防ぐことが多い。なお、最尤推定などをそのまま適用するとパラメータ数は
最尤推定の考えに基づいてパラメータを推定する方法として最も直接的な方法は、MCMCサンプリングを用いる方法である[6, 7]。この方法ではまずパラメータをランダムに初期化し、そのパラメータに基づいてMCMCサンプリングによってデータを多数生成する。そして、その生成されたデータ頻度から計算されるPi(x)やPi,j(x,y)が、実データから観測されるfi(x)やfi,j(x,y)とどの程度異なるかを計算する。その後、そのずれを利用して尤度が大きくなるようにパラメータのアップデートを行う。そしてアップデートされたパラメータに基づいて、再びMCMCサンプリングによってデータを生成する。このMCMCサンプリングとパラメータのアップデートをパラメータが収束するまで繰り返し、最終的に収束した解を推定解とする。この方法は高精度にパラメータを推定可能である一方で、多数のサンプリングを必要とするために計算に大変時間がかかるという問題がある。
MCMCサンプリングよりも高速な手法として、擬尤度最大化法が良く用いられている[8, 9, 10, 11, 12]。この方法では、目的関数として対数尤度
その他のパラメータ推定手法として、適応的クラスター拡張法[14, 15, 16]や平均場近似法[17, 18]、最小確率流法[19]などが提案されている。しかしながらこれらの手法はいずれも精度と速度の間にトレードオフが存在する。また、高速な代わりに推定精度が低い方法(平均場近似法や擬尤度最大化法など)であっても、特に強い依存関係にあるペアについては高精度で検出できるという報告も存在する[7, 13]。そのため、自らが適用したいデータセットのサイズや問題設定に応じて、どの手法を用いるべきか選択する必要がある。モデルや学習方法の詳細については[3, 13, 20]などをご参照いただきたい。
逆イジング法の生命情報解析への応用例としてもっとも盛んに行われている研究は、タンパク質立体構造解析への応用である。この解析では、アミノ酸配列のマルチプルアライメントデータを、各アミノ酸配列が行、各カラムが列である行列データであるとみなし、行列の各要素はギャップを含めた21文字のうちのどれか1つを取る離散的なデータであると捉えた上で逆イジング法を適用する。ここでタンパク質の立体構造を考えると、各アミノ酸が他のアミノ酸とは独立に進化するとは考えにくく、特に立体構造上近接する部位は互いに依存して共進化していることが期待される。このことから逆に、逆イジング法によって依存関係にあるカラムのペアを抽出すると、その部位はタンパク質立体構造内のコンタクト部位となることが期待される。逆イジング法を利用した構造解析手法はDCA(Direct Coupling Analysis)やEC(Evolutionary Coupling)とも呼ばれ、本総説では今後この解析手法をDCAと呼ぶこととする。
DCAはM. Weigtらにより2009年に初めて提案された[21]。提案当初は、相互作用することがあらかじめわかっているタンパク質のペアが与えられた時に、実際にコンタクトするアミノ酸同士を高精度に推定する手法として提案された。その後、相互作用するタンパク質のペアが未知の状態からDCAを用いて相互作用するペアを予測する方法が開発されるなど、DCAを用いたタンパク質相互作用の研究は盛んに進められた[22, 23, 24, 25, 26, 27]。現在では、DCAに基づいた、大腸菌プロテオームレベルでの大規模な相互作用予測の結果が発表されている[28]。また相互作用予測のみならず、DCAを利用したタンパク質の立体構造予測についても多くの研究がなされている。この方法はD. Marksらにより2011年に初めて提案され[29]、DCAにより予測したコンタクト部位の情報とフラグメントアセンブリ法などの構造予測手法を組み合わせることで、アミノ酸配列のみから高精度に立体構造を予測することが可能である[30, 31, 32](図2A)。またDCAは、タンパク質の構造研究のみならず、RNAの立体構造予測やRNA-タンパク質相互作用予測にも応用されており、タンパク質の構造解析と同様高い性能を示すことが報告されている[33, 34, 35]。なおM. WeightとD. Marksの両名は2010年代を通して逆イジング法の生命情報解析研究を牽引してきた研究者であり、現在でも逆イジング法に基づく論文を多く発表している。
しかし、DCAを利用して立体構造予測・相互作用予測を行うためには、そのマルチプルアライメントにおいて多くのサンプル数(アミノ酸配列の数)が必要であるため、あらゆるアミノ酸配列に対して適用できるわけではないという問題点が存在する。近年では、大規模なメタゲノムデータの中からアミノ酸配列のホモログを多数集めることでサンプル数を増やす方法[36]や、網羅的な配列変異実験を行い、その際に機能を失わなかった配列をサンプルに加えることでサンプル数を増やす手法[37]などが提案されており、DCAを適用できるアミノ酸配列数を増やそうとする試みが進められている。特に後者は、ある系統群特異的に存在するタンパク質であるため、自然界に存在するアミノ酸配列だけでは原理的にDCAを適用できないようなケースにおいても有効であると期待されている。
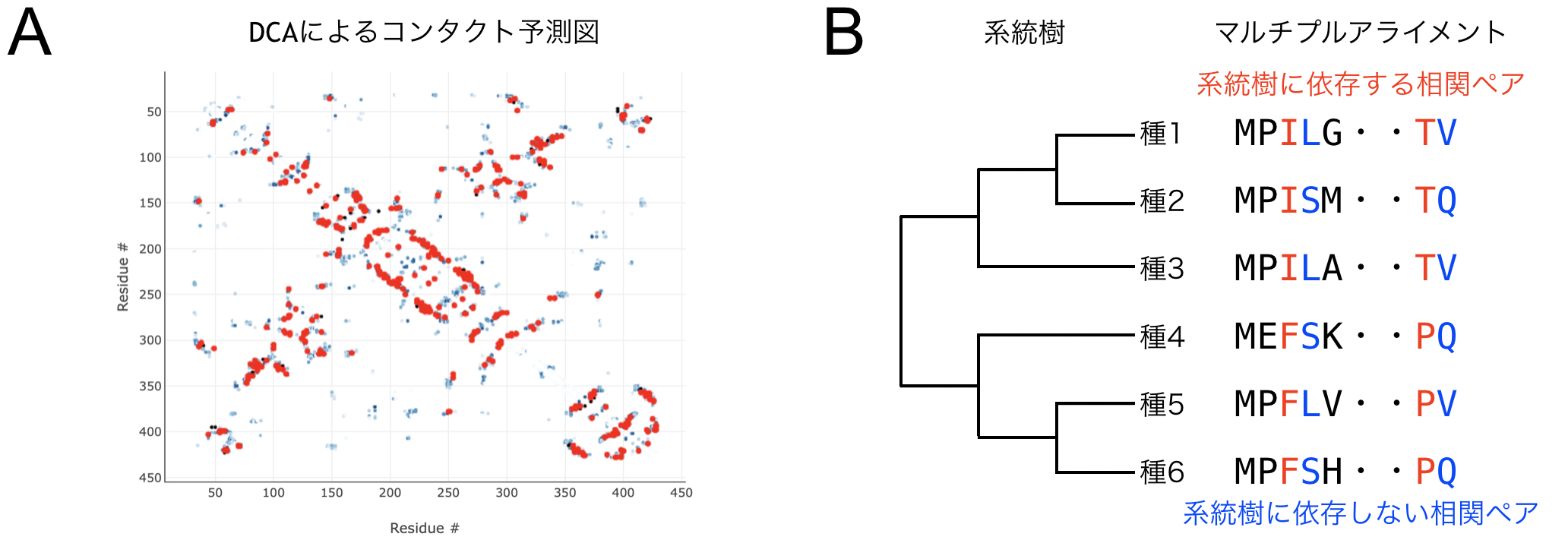
(A)ウサギミトコンドリアのアスパラギン酸アミノ基転移酵素に対して、DCAによりコンタクト部位を予測した図。x軸、y軸は共にアミノ酸配列の各残基を表す。青丸が実験的に解かれた立体構造から計算された実際のコンタクト部位、赤丸がDCAによる予測と実際のコンタクト部位が合致した箇所、黒丸がDCAによって予測されたが実際のコンタクト部位ではなかった箇所を表す。計算はEVCouplings Serverを利用して行った[38]。(B)アミノ酸配列間に存在する系統関係の模式図。種間の系統樹とアミノ酸配列のマルチプルアライメントを表す。
DCAは計算機的に立体構造を予測するために使われるだけではなく、実験的に立体構造を決定する際の参照情報として利用されることもある。[39]では、ペプチドグリカン合成酵素であるRodAタンパク質の構造をX線結晶構造解析で決定する際、DCAにより得られたコンタクト情報に基づいて分子置換法でその位相を決定している。また[40]では、NMRを利用した構造決定において、配列長の長いタンパク質ではNMRによるスペクトルデータとDCAの情報を統合することでより精度良く構造決定を行うことができると報告している。
また逆イジング法に基づいて、タンパク質の機能解析を行う研究も存在する。この研究では、逆イジング法により学習された生成モデルに基づいて、アミノ酸配列が変化した時に機能がどの程度失われるかを予測する。これは、アミノ酸を変化させる前後のデータの出現確率を計算し、変化後にデータの出現確率が大きく低下するならば、それは配列が適切な構造を取れなくなることを意味するので機能が失われているだろうという推論に基づく[41, 42, 43, 44, 45]。これらの研究による予測はある程度の予測精度があることから、イジングモデルがアミノ酸配列の生成モデルとしてある程度妥当であることを示している。しかし、機能変化の予測が目的であれば、学習により得られたペアの依存関係のパラメータの解釈の必要がないため、解釈は難しいがより高精度な生成モデルが得られる深層学習を利用した手法も提案されている[46]。
近年のDCAの研究では、逆イジング法のモデルを拡張することで、より高い精度を達成しようとする研究も進められている。たとえば[47]では、二項間の関係だけではなく三項間の関係までモデルに含めてパラメータを学習することで、より高い精度でコンタクト部位を予測することができたと主張している。なおこの研究では、単純に三項間に拡張するだけでは推測すべきパラメータが多くなりすぎるため、アミノ酸を極性などの基準で二値化した上でパラメータを学習している。一方で[7]では、二項間の関係のみを見た通常のDCAで得られたモデルだけでも、現実データで観測されている三項間の依存関係の統計量を十分に再現できたと報告している。一見矛盾する報告ではあるが、[47]と[7]では使用した学習法やデータセット、評価基準などが異なっているため単純な比較を行うことはできない。三項間関係を含めたモデルがタンパク質構造解析において有効であるか否かについては、更なる調査研究が必要である。なお、三項間関係をモデルに含む拡張が有効であるかは適用するデータセットに依存する問題であるため、仮にタンパク質の構造解析において有効でなかったとしても、他のデータ解析においても有効でないということを意味するものではないことには注意が必要である。
DCAは学習においてタンパク質の立体構造情報を利用しない教師なしの学習手法であるが、DCAで学習されたパラメータを特徴量、構造データを教師データとした教師あり学習を行うことで、更なる精度向上を試みる手法も提案されている[48, 49, 50]。これらの方法では、複数の学習方法で得られたDCAのパラメータをそれぞれ特徴量として利用する以外に、タンパク質の二次構造や溶媒接触性などの情報も特徴量として利用することでより精度を向上させている。なおこれらの情報は、タンパク質のアミノ酸配列データのみから十分高精度に予測可能であるため、追加で実験を行ってこれらのデータを取得する必要がないという点が重要である。第三者によるベンチマークテストの結果では、この教師あり学習と統合した手法は教師なし学習のみの手法に比べて予測精度が良かったことを報告している[51]。利用する学習器としては、現在のところ深層学習を用いる手法が性能がよいと考えられている。
逆イジング法のモデルは、サンプル同士が独立であることを暗に仮定したものである。しかしDCAにおいては、アミノ酸配列間において進化的な関係性が存在しているため、サンプル同士が独立という仮定は原理的に成り立たない(図2B)。そのために、立体構造内のコンタクト部位に由来するカラムのペアだけではなく、たまたま進化史を共有しているだけのカラムのペアも系統的バイアスとしてDCAにより検出されてしまうという問題点がある[52]。この系統的バイアスを補正するために、アミノ酸配列データセット間において配列類似度が高いペアが存在する場合、その配列の寄与を小さくしてパラメータ学習を行う系統的重み付け法などが利用されている[53]。この方法は簡単な補正法であるためモデルに取り入れやすいという長所がある一方、ヒューリスティックな手法でありアミノ酸配列の進化関係を明示的にモデルに組み込んでいるわけではないという問題点がある。実際にベンチマーク実験の結果からは、系統的重み付け法は性能改善にはわずかにしか寄与していないことが示唆されている[53]。そのため、系統樹を明示的にモデルに組み込んだ逆イジング法の開発が必要であるが、精度を大きく改善するような手法は現在のところ提案されておらず、今後の重要な研究課題である[54]。
系統的バイアスに関する興味深い理論研究として、C. Qinらによるランダム行列理論に基づく研究が挙げられる[55]。この研究では、ペア間の分散共分散行列の固有値の分布に着目する。この時、もし相互作用由来の依存関係が存在せず系統バイアスによる依存関係しか存在しないならば、その固有値の分布は理論的にべき乗則に従うことを示している。そのため、実際の相互作用に由来する部分とは、そのべき乗則から外れている部分であると結論づけている。
これまで紹介したように逆イジング法はタンパク質立体構造解析において盛んに利用されている手法であるが、その目的は本来「データのとる値が離散(カテゴリカル)である行列データから依存関係にある列のペアを感度良く検出する」ということであるため、アミノ酸配列データに限らず多様なデータセットに対して適用可能である[56]。そもそも先述した通り、生命データ解析への適用の先駆けとなった研究はE. Schneidmanらによる神経活動データの解析研究である[4]。この研究では、脊椎動物の網膜の神経細胞集団の発火パターンを、各タイムポイントを行、細胞を列とし、細胞があるタイムポイントで発火したか否かを二値で表現した行列データと捉える。この論文ではまず、各細胞間の発火パターンの相関係数はほとんどが大変小さいことから、細胞間にはほとんど相互作用がないように見えることを示している。しかしながら、発火パターンの生成モデルを考えると、各細胞を独立と仮定したモデルよりもイジングモデルを想定した方がデータへの当てはまりがよいことから、このような神経細胞集団の内部にも実はネットワーク構造が存在することを指摘している。この研究以降、逆イジング法は神経活動データ解析において一般的な解析手法となっている[57, 58]。
ゲノムワイド関連解析(GWAS)への適用例も存在し、この場合、個体を行、SNPを列とした行列データとして逆イジング法を適用する[59, 60, 61, 62]。たとえば[62]では、淋菌Neisseria gonorrhoeaeを対象に、その抗生物質耐性に関与する遺伝子座位の相互作用(遺伝学ではエピスタシスと呼ばれる)を、逆イジング法を利用して検出している。その結果として、既知の抗生物質耐性遺伝子が関わるエピスタシスも数多く検出されたものの、今まで抗生物質耐性に関与すると報告されていなかった遺伝子のみで構成されるエピスタシスが大半を占めたことを報告している。なお、現在報告されているGWASへの適用研究はいずれも、微生物を対象としたものでありヒトなどの真核生物を対象にした研究は存在していない。これは、真核生物のゲノムサイズではSNP数が多すぎるため、必要なサンプルサイズや計算時間の観点から逆イジング法をそのまま適用することが難しい点にあると思われる。よって、ヒト疾患研究などに逆イジング法を適用したい場合には、SNPのクラスタリングや事前の絞り込みなどのデータ前処理、または高速なパラメータ推定手法の開発などが必要であると考えられる。
また生命データ解析のみならず、社会科学分野のデータ解析への応用例なども存在する。例として、アメリカ合衆国の最高裁判所における裁判官の判決の傾向をモデル化した研究があげられる[63]。この研究では判決を行、各裁判官(9名)を列とし、各裁判官が判決に賛成したか反対したかを二値で表現した行列データとして捉える。そして、このデータに対して逆イジング法を適用することで裁判官同士での判決の類似傾向を抽出し、その政治的傾向との関係性などを解析している。
本総説では、データの取る値が離散(カテゴリカル)である行列データから依存関係にある列のペアを高感度に検出する手法である逆イジング法の紹介を行った。まず逆イジング法のモデルと学習方法について解説を行い、これら学習方法の間には精度と速度のトレードオフがあるため、使用するデータや目的に応じて使い分ける必要があることを議論した。また、逆イジング法の生命情報解析への応用例として、主にタンパク質立体構造解析への適用を中心に具体的な研究例を解説した。一方で、逆イジング法は離散値の行列データさえあれば適用可能であることから、広い応用例が存在していることを紹介した。
今後の研究としてはまず、逆イジング法が未だ適用されていない離散値行列データに逆イジング法を適用し、その有効性を検討することが重要である。また、タンパク質立体構造解析研究において研究がなされた、三項間関係の解析や教師あり学習との統合解析は適用分野を限定しない一般的な解析手法であるため、これらの手法を他のデータセットに適用することも興味深い研究課題である。加えて、新しいデータセットに逆イジング法を適用する際には、現在の学習方法では精度・速度が実用的でないことも考えられるため、より優れた学習方法を考案していくことも必要である。
タンパク質立体構造解析への応用研究においては、系統樹情報の考慮による精度向上が最重要な研究課題であると考えられる。系統関係を考慮した形質の比較手法の研究は、系統学において古くより議論されている課題であり、系統比較法(Phylogenetic comparative methods)と呼ばれる様々な手法が提案されている[64, 65]。この手法と逆イジング法の統合は問題解決の糸口となることが期待されるが、シンプルな統合は計算時間を大幅に増加させるため実用的ではないことが予想される。よって、ある程度の近似を伴う、しかし実用的なヒューリスティクスを提案することが重要かもしれない。また、現在逆イジング法の入力データとなっているマルチプルアライメントは決定的なデータとしてみなされているが、このマルチプルアライメントはアミノ酸配列群からソフトウェアにより推定されたものであり、実のところ不確実性を伴うデータである。このようなアライメントデータに付随する不確実性を考慮したうえでモデル化をおこなう[66]ことで、コンタクト部位の推測精度が向上すると考えられる。
 |
福永 津嵩 2016年 東京大学大学院新領域創成科学研究科メディカル情報生命専攻博士後期課程を修了。博士(科学)。早稲田大学理工学術院学術振興会特別研究員を経て、2017年より東京大学大学院情報理工学系研究科コンピュータ科学専攻助教としてバイオインフォマティクスの教育・研究に当たっている。特に、機械学習や文字列解析などの情報学的手法に基づいた、ゲノム配列解析ソフトウェアや機能未知遺伝子推定ソフトウェアの開発研究を行なっている。 |