行列・テンソル分解によるヘテロバイオデータ統合解析の数理

―第1回 行列分解―

Abstract

生命科学分野で取得されるデータ集合は、雑多（ヘテロ）な構造になり、ヘテロなデータ構造を扱える理論的な枠組みがもとめられている。本連載では、汎用的なヘテロバイオデータの解析手法である行列・テンソル分解を紹介していく。第1回では、第2回以降のアルゴリズムの基礎となる、1行列での行列分解について説明する。

ヘテロバイオデータとは

生命は幾つもの生体分子（例：RNA、DNA）や現象（例：SNP、CNV）が複雑に関連しあったネットワークで構成される。この大規模なネットワークに関わる生体分子や現象を全て同時に計測することは現在までのところできていない。そのかわりに、生命科学研究ではオミックスと称し、特定の生体分子や現象のみに限定した上で、それらを網羅的に計測するアプローチがとられている。このようなアプローチで得られた雑多（ヘテロ）なデータ集合から、いかに生命現象の全体像を導き出せるかが、今後のバイオインフォマティクス研究の重要な課題の一つだと考えられる。

生命科学データのヘテロ具合は、他のデータサイエンス分野と比べても群を抜いている。例えば、1細胞RNA-Seqデータをとっても、どの遺伝子がどの細胞で発現したのを計測した遺伝子発現量行列だけでなく、その行列が異なるバッチ、実験条件、生物種などで複数あったり、遺伝子に紐づいたパスウェイ情報、下流のターゲット遺伝子、更にそのターゲット遺伝子に関連した遺伝子機能まであったり、細胞に紐づいた情報としても、別のオミックスデータや、細胞の空間配置、その細胞の計測に関する実験的メタデータなどもある（図1）。このような複雑に繋がりあったデータ集合を、どのように解析すべきなのかは自明ではなく、多くの場合、個々に解析をした後に、解析結果を見比べる“ベン図型”アプローチがとられる。例えば、1細胞RNA-Seq解析でよく行われるベン図型アプローチとしては、1細胞マルチオミックス解析で、RNA-Seqで検出された発現変動遺伝子の領域と、ATAC-Seqで検出されたオープンクロマチン領域同士でベン図をとったものや、細胞型ごとの機能アノテーション解析で、まず細胞型ごとに変動する発現変動遺伝子を特定し、次にそれら遺伝子に関わる機能タームをエンリッチメント解析する2ステップの解析などが挙げられる。本連載では、そこからさらに進んで、複数のデータを同時に扱うアルゴリズムを紹介する。このようなアプローチをうまく活用することで、ノイジーなデータからのシグナル検出を他のデータでサポートできたり、あるデータの欠損値を他のデータとの兼ね合いで補完できたり、複数のデータ間を跨いだ予測モデルを構築できるなど、ベン図型アプローチでは実現できない事が可能となる。

図１ ヘテロな1細胞RNA-Seqデータ

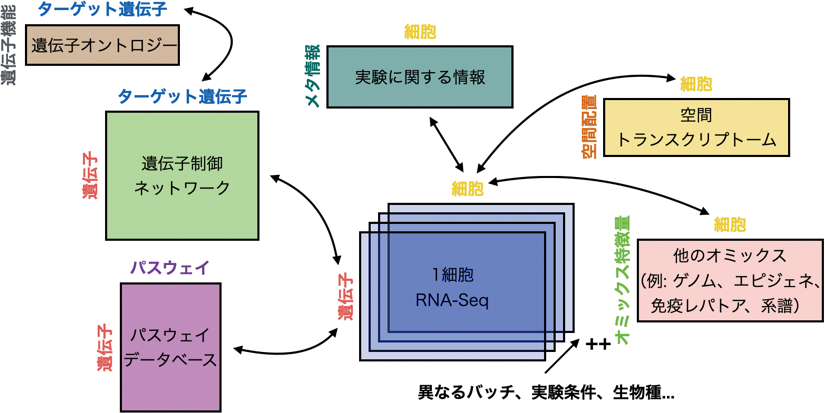
遺伝子×細胞の遺伝子行列に加え、遺伝子、細胞に関する他のデータが互いに繋がりあっている。

本連載では、ヘテロなデータに特化したアルゴリズムを紹介する。なお、近年Webデータマイニング業界では、Heterogeneous Information Networks（HINs［1］）というキーワードのもとで、雑多なデータ集合をどのように解析すべきなのか議論されている。HINsの定義は、あるグラフのノードの種類が2種類以上、またはエッジの種類が2種類以上の場合とされているため［2］、本連載でもこの定義を継承する。

本連載で扱うデータは全て類似度行列・テンソルとする。それ以外の尺度（例：距離）は何らかの方法で類似度に変換してから利用するものとする（例：ユークリッド距離⇆コサイン類似度［3］/カーネル類似度［4］、木⇆セマンティック類似度［5］）。紹介するアルゴリズムは、行列分解やテンソル分解とする。これは、著者が知る中で、最も汎用性が高く、どれだけデータ構造が複雑化しても統一的に解析できる点や、結果の解釈が容易で、実装しやすく、高速化しやすいアルゴリズムを著者が好む傾向にあるためである。ただし、同様の問題を別の理論的枠組み（例：深層学習、マルチカーネル学習、ランダムウォーク、ベイズ推定）で解くことは可能である［6, 7, 8, 9, 10］。一般論として、パラメーターが多い複雑な非線形モデルの方が、精度で勝る場合も多い。ただし、どのドメインデータのどの問題においても、同じ枠組みが適用できることを知ることは、今後ヘテロなバイオデータを扱うであろう、読者の理解を助けるものと考えている。なお、紙面の都合上、紹介するアルゴリズムの厳密な議論（目的関数の導出、初期値・ハイパーパラメーターの設定方法、解の一意性、生物学的解釈、実データでの性能比較など）はあまり説明できないため、詳細は引用文献を参照して欲しい。また、多くの行列・テンソル分解では、1つの目的関数に対して最適化手法が複数あり、これらは本来分けて考えるべきものであるが、紙面の都合からよく知られた代表的な最適化手法のみを紹介していることや、できるだけ最先端の手法を紹介するために、バイオインフォマティクス分野でまだ利用されたことが無い手法も一部とりあげていることにも留意してほしい。

1行列での行列分解

まずは、この先で説明する全てのアルゴリズムで基本となる、1つの行列における行列分解、特に利用実績が多いPrincipal Component Analysis（PCA）、Non-negative Matrix Factorization （NMF）、Independent Component Analysis （ICA）を説明する［11］。ここでは、n×pの行列Xを分解する。例えば、RNA-Seqデータであれば、nはサンプル数、pは遺伝子数であり、行列の各要素は遺伝子発現量を表す。行列分解では、この行列Xを以下のように近似する。

  

$$\begin{array}{}\text{（1）}& X\fallingdotseq {\mathit{UV}}^T\end{array}$$

ここでUは n×kの行列、Vはp×kの行列である。ただし、kは1≦k≦min（n, p）を満たす整数とする。または、U、Vの列ベクトルの長さが1となるように正規化し、その分の重みをΛ（k×kの対角行列）の対角要素にまとめた形で

  

$$\begin{array}{}\text{（2）}& X\fallingdotseq {\mathit{U\Lambda V}}^T\end{array}$$

と説明される場合も多い。このような式が何を意味しているのか、なぜ分解をするのかについて考えてみる。ここでは、読者の多角的な理解を助けるため、「パターンの和としての行列分解」と「射影としての行列分解」を説明する。これらは、本質的には同じ計算を違った角度で見ているだけではあるが、アルゴリズムによっては、どちらかの方法で解釈した方が素直に理解しやすいため、本稿ではこのようなやり方を導入した。なお、Nguyen, N. D.らは、前者のことをFactorizationベースの手法、後者のことをAlignmentベースの手法と分類している［12］。

まずは、パターンの和として行列分解を説明する。行列を分解するということは、すなわち、行列に含まれるパターンを取り出すということである（図2）。例えば、式（2）の右辺をベクトルで書くと、${\sum }_{i=1}^k{\lambda }_i{u}_i{v}_i^T$となり（λ_iはΛのi番目の対角要素）、Uのi番目の列ベクトルu_iとVのi番目の列ベクトルv_iの直積（outer product）$u_i{v}_i^T$（= u_i⊗v_i）に、λ_iが重みづけされた形で表現できる。パターンの和としての行列分解の文脈では、U、Vは因子行列と呼ばれる。u_iは行列のうちどの行が値や変動が大きい（または小さい）のか、v_iはどの列が値や変動が大きい（または小さい）のかを示すベクトルである。λ_iは各パターンの大きさを示すスカラである。

図２ パターンの和としての行列分解

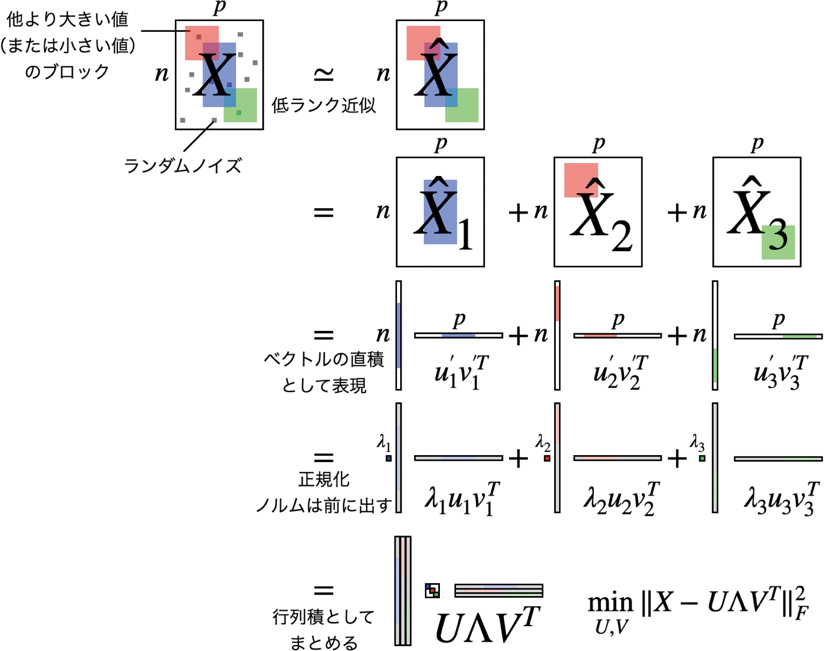
行列分解とは、データ行列を少数のパターン（ランク1行列）の和として近似することに相当。

これらのベクトルやスカラを利用して、さらにデータ解析を進める事ができ、UやVを細胞や遺伝子の特徴量抽出や、可視化、クラスタリングに利用したり、Λでどのパターンまでが情報を持っていそうか確認できる。少数のパターンの和として、データ行列を近似し、それにより行列のランクが下がるため、低ランク近似とも呼ばれる。また、kの値次第では、元のp次元よりも次元が落ちるため、次元圧縮とも呼ばれる。うまくシグナルの特徴をとらえる事ができたら、ノイズを回避してシグナルだけを取り出せるため、ノイズ除去しているとも言える。

実際にパターンを取り出すためには、Xとの誤差がなるべく小さくなるように、以下のようなU、Vに関する目的関数を最適化することになる。

  

$$\begin{array}{}\text{（3）}& \underset{U,V}{\min }\parallel X-{\mathit{U\Lambda V}}^T{\parallel }_F^2\end{array}$$

なお、このままではこの最適化問題を閉じた形で解析的に解くことはできず、何かしら制約を設定することになる。PCAでは、列ごとの平均値を0に中心化したデータ行列Xに対して、U^T U = V^T V = I_kを制約とし（正規直交性、I_k : k×kの単位行列）、後ほど説明する固有値分解（Eigen Value Decomposition; EVD）や特異値分解（Singular Value Decomposition; SVD）で最適化する［13, 14］。

NMFでは、非負値データ行列Xを分解する。因子行列U、Vの非負値性（U, V ≥ 0）を制約とし、式（1）をU、Vで各々微分して勾配をもとめ、勾配法でU、Vを収束するまで交互に推定する最適化手法Multiplicative Update Rule（MU則）を利用して以下のように最適化する ［15, 16］。

  

$$\begin{array}{}\text{（4）}& U\leftarrow U\circ \frac{\mathit{XV}}{{\mathit{UV}}^{T}V}\end{array}$$

  

$$\begin{array}{}\text{（5）}& V\leftarrow V\circ \frac{X^{T}U}{{\mathit{VU}}^{T}U}\end{array}$$

ただし、ここで∘は2行列の要素ごとの積（アダマール積）、/は2行列の要素ごとの商である。

次は、射影として行列分解を説明する。まずは簡単に2次元空間にあるデータ点を、1次元空間に射影する場合を考える（図3）。ここで図3の赤線で示した単位ベクトル（原点を通る長さ1のベクトル）v上に、データx_nを射影する。内積の定義（a∙b = |a||b|cosΘ）とコサインの定義から、原点Oから射影先のx_nまでの距離は、x_nとvの内積値$x_n^{T}v$になる。1からnまでのx_nを一度にvに射影したい場合は、Xvとすれば良い（線形写像［17］という）。p次元からk次元に射影する場合も同様にXVとするだけである（図4）。射影先のX（スコアという）をUとおけば、

  

$$\begin{array}{c}\mathit{XV}=U\\ \text{（6）}& X={\mathit{UV}}^{\text{+}}\end{array}$$

となる（V⁺は行列Vの一般逆行列［18, 19］）。すなわち、射影としての行列分解の文脈では、行列分解の式（1）の右辺のUはXのスコア、Vは射影行列（ローディング、または因子負荷量ともいう）である。PCAの場合は、列直交性からV⁺ = V^Tであるため、さらに簡単にX = UV^Tとなり、式（1）の形と一致する。

図３ 射影のイメージ

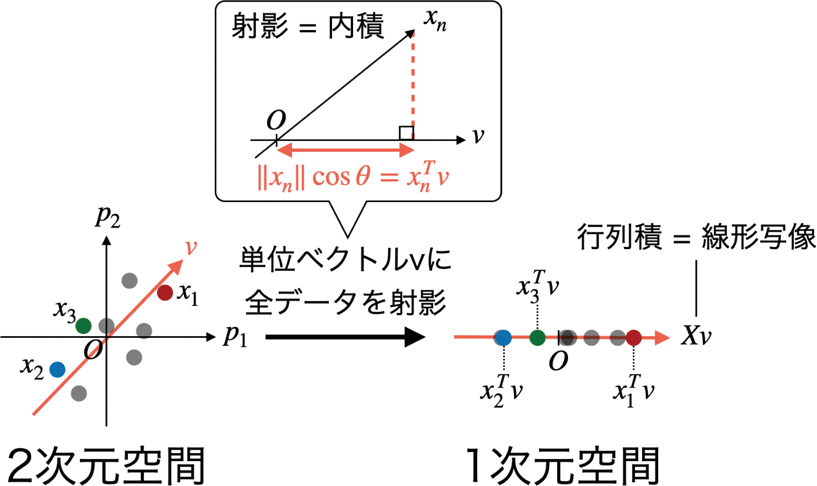
行列積とは、データをベクトル上に射影することに相当。

図４ 射影としての行列分解

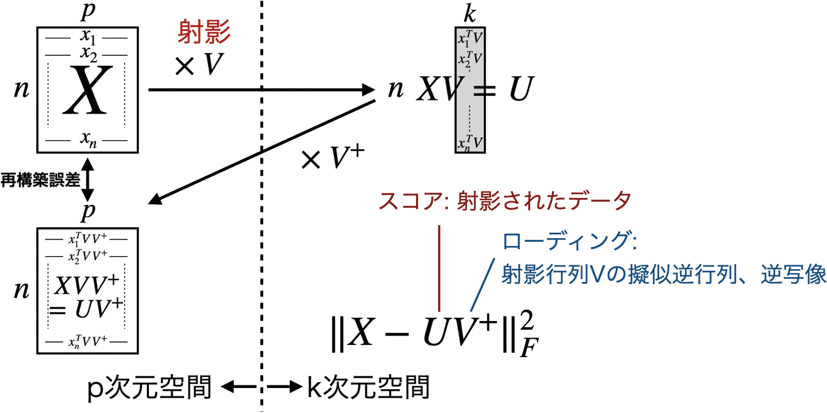
行列分解とは、低次元に射影して、再構築した際の誤差を最小化することに相当。

さて、このVをどのような基準で推定するかが問題となるが、PCAの場合は、列ごとの平均値を0に中心化したデータ行列Xを式（1）のように分解する際に、Uの列ベクトルの分散の総和が最大となるようにVを求める。Vの正規直交性（V^T V = I_k、I_k : k×kの単位行列）という制約の下で、var（XV）を最大化する問題はラグランジュ未定乗数法より、Xの分散共分散行列${\mathrm{\Sigma }}_{\mathit{XX}}=\frac{1}{n}{X}^{T}X$のEVD

  

$$\begin{array}{}\text{（7）}& {\Sigma }_{\mathit{XX}}V=\mathit{VS}\end{array}$$

として解く事ができる（Sは固有値を対角要素にもつk×kの対角行列）。右辺のVを左辺に移項した以下の式

  

$$\begin{array}{}\text{（8）}& V^T{\mathrm{\Sigma }}_{\mathit{XX}}V=S\end{array}$$

は、Σ_XXの対角化といい、対角要素を最大化させることから、トレース（行列の対角要素の和）を使って、

  

$$\begin{array}{}\text{（9）}& \underset{V}{\max }\mathit{tr}\left(V^T{\mathrm{\Sigma }}_{\mathit{XX}}V\right)\end{array}$$

と書くこともある。式（3）を以下のように変形すると、式（3）の誤差最小化と式（9）の分散最大化は同じ意味である事がわかる（Cは定数）。

  

$$\begin{array}{c}\parallel X-{\mathit{U\Sigma V}}^T\parallel {}_F^2\\ =\parallel X-{\mathit{XVV}}^T\parallel {}_F^2\\ =\mathit{tr}((X-{\mathit{XVV}}^T){(X-{\mathit{XVV}}^T)}^T)\\ =\mathit{tr}({\mathit{XX}}^T)-\mathit{tr}({\mathit{XVV}}^T{X}^T)-\mathit{tr}({\mathit{XVV}}^T{X}^T)+\mathit{tr}({\mathit{XVV}}^T{X}^T)\\ \text{（10）}& =-\mathit{tr}(V^T{\mathrm{\Sigma }}_{\mathit{XX}}V)+C\end{array}$$

$\parallel X-{\mathit{XVV}}^T\parallel {}_F^2$ のような表記は、再構築誤差とも呼ばれ、一度低次元に射影したX（XV）を同じVを用いて、元の次元に再構築している。深層学習の用語を借りれば、射影するほうのVはエンコーダー、再構築するほうのV^Tはデコーダーである。再構築されたXVV^Tは行列のサイズとしてはXと同じであるものの、Vの次元（k）分の膨らみしかないことに注意してほしい。なお、列ごとの平均値を0にする中心化に加え、列ごとの標準偏差が1になるように、標準偏差で割る操作（標準化）も行った変数における分散共分散行列は相関係数行列となる。相関係数行列でのPCAは、単位や値のスケールが異なる変数をまとめて解析する際に有用であるが、ここではこれ以上扱わない。${\frac{1}{n}X}^{T}X$ではなく、$\frac{1}{n}{\mathit{XX}}^T$の方はグラム行列（G_XX）と言い、U = AXV（Aは対角行列）と仮定すると、式（7）より、

  

$$\begin{array}{c}X{\mathrm{\Sigma }}_{\mathit{XX}}V=\mathit{XVS}\\ \text{（11）}& G_{\mathit{XX}}U=\mathit{US}\end{array}$$

となることから、UはG_XXの固有値ベクトルであり、かつΣ_XXと固有値を共有していることがわかる。このG_XXのEVDはDual PCAやQモードPCAと呼ばれる。Uの列ベクトルを単位ベクトルとするとA²=（nS）⁻¹となることから、UとVの関係性は、以下のようにしてまとめることができる。

  

$$\begin{array}{}\text{（12）}& X={\mathit{U\Lambda V}}^T\end{array}$$

この形式はSVDと言われ、k×kの対角行列Λの対角要素は特異値と呼ばれる。特異値と固有値には、Λ²＝nSという関係がある。通常のPCA（Rモードという）で得られた固有ベクトルVと、QモードPCAで得られた固有ベクトルUは式（12）により容易に変換できることから、Σ_XXとG_XXのサイズが小さいほうで計算することで、計算量を削減できる。

なおICAの場合は、列ごとの平均値を0に中心化したデータ行列Xを式（1）のように分解する際に、Uの列ベクトルが互いに独立になるようにVを推定する。ICAの問題設定は、PCAやNMFと比べるとやや特殊で、制約はUのみに設定する。Uの列ベクトル間にいかに独立性をもたせるかで様々なアルゴリズムがある。ICAではまず、計算量の削減と最適化の収束性向上のための前処理として、以下のように白色化という処理を行う。

  

$$\begin{array}{}\text{（13）}& X_{\text{white}}={\mathit{XVS}}^{-1/2}\end{array}$$

ただし、Xは列ごとの平均値を0に中心化したデータ行列、VはPCAにおける固有ベクトル、Sは固有値である。Vの列数kをフルランク（min{n, p}）よりも小さい値にすることで、Xの次元圧縮も同時に行える。白色化により、X_whiteの分散共分散行列は以下のように単位行列になるため球状化とも呼ばれる。

  

$$\begin{array}{cc}\frac{1}{n}{X}_{\text{white}}^T{X}_{\text{white}}& =\frac{1}{n}{S}^{-1/2}{V}^T{X}^T{\mathit{XVS}}^{-1/2}\\ & =S^{-1/2}{V}^T{\mathrm{\Sigma }}_{\mathit{XX}}{\mathit{VS}}^{-1/2}\\ & =S^{-1/2}{V}^T{\mathit{VSV}}^T{\mathit{VS}}^{-1/2}=I\end{array}$$

相互情報量最小化でスコア間の独立性を定式化するInfomax［20, 21, 22, 23］では、以下のように自然勾配法でUを逐次的に最適化する。

  

$$\begin{array}{}\text{（14）}& U_{t+1}\leftarrow U_t+\eta \left(t\right)\{I-\phi (X_{\text{white}})X_{\text{white}}{}^T\}{U}_t\end{array}$$

（tは逐次最適化の反復ステップ、η（t）は定数か1/tなどの減衰関数、φ（X）はtanh（X）など何らかの非線形関数）。非ガウス分布性を最大化することで、スコア間の独立性を定式化するFastICA［20, 21, 22, 23］では、以下のように不動点法でUのi番目の列ベクトルu_iを逐次的に最適化する。

  

$$\begin{array}{}\text{（15）}& u_i\leftarrow E\left(\phi \text{'}(u_i^T{X}_{\text{white}})\right)u_i-E\left(\mathit{X\phi }(u_i^T{X}_{\text{white}})\right)\end{array}$$

ただし、Eは期待値であるが標本平均で代用する。Uの列ベクトルは互いに直交になるように、最適化時にDeflation（Gram-Schmidt-like Decorrelation）やLöwdin Symmetric Orthogonalizationといった処理が入る。

おわりに

今回は、1行列における代表的な行列分解アルゴリズムであるPCA、NMF、ICAを「パターンの和としての行列分解」と「射影としての行列分解」という2つのアプローチで説明した。これらの分解のイメージは、第二回以降の行列同時分解やテンソル分解の理解にも役立たせることができる。

最後に、本稿で紹介した行列分解手法の利用ガイドラインを示しておく。アルゴリズムにより、行列分解の結果に違いが見られる。どの手法が最も優れているのかを決めるのは難しく、データや状況、その行列分解で何をしたいのかに依存するが、大まかな各手法のメリット・デメリットを以下に記す。

まずPCAのメリットとしては、UやVが無相関であるため（直交=内積が0の時、Pearsonの相関係数も自ずと0となるため）、そうでない場合（斜交）と比べて、似たようなパターンが取り出されづらい点が挙げられる。また、Eckart-Young定理［25］として知られるように、SVDは式（2）を最も最小化させることが保証されている。ただしデメリットとしては、直交制約が不利に働いたり、負値を含んだベクトルが解釈しづらい場合もあることが挙げられる。このあたりの改善は、トピックモデル［26］の発展とも関連が深い。またSVDの符号の曖昧さ（Sign Ambiguity）、すなわち$u_i{v}_i^T$も正負が反転した${(-u}_i)({-v}_i^T)$も数学的にはまったく同じ解であるため、UやVの中に正の方向に大きい値と、負の方向に大きい値があった時に、どちらを注目すれば自分が注目したい方向で変動した特徴量が手に入るのかがわかりづらいことが挙げられる。

一方、NMFのメリットとデメリットはかなりはっきりしている。メリットとしては、得られるパターンが解釈しやすいことである。Xが非負値でかつ正の方向に変動したパターンにしか興味が無い場合は、NMFではUやVのうち正の方向に大きい要素のみに注目すれば良い。また、正規化されたUやVは、確率ベクトルとして解釈することができ［27］、そのままクラスタリング手法として利用することも可能である［28］。ただし、デメリットとしては、非負値性の仮定が崩れる場合、例えばXが負値を含む場合や、負のパターン（例：負の方向に変動した遺伝子発現）もしくは正のパターンと負のパターンの対比（例：A/Bコンパートメント［29］）にも興味がある解析には適さない。またNMFで得られたパターンは、パーツごとに分離されがちで、この特徴はメリットにもデメリットにもなり得る。例えば、NMFは当初顔画像の解析に利用されたが、目や鼻など、顔を構成する小さいパーツを分離し、顔の輪郭のような大きいパターンは取り出さない傾向になることが指摘されている［15］。また大域的最適解が得られる保証が無いため、初期値を変えて複数回アルゴリズムを実行し、ばらつきを調べたり、最も目的関数の値が小さい解を使うなど、やや工夫が必要となる。

ICAは、音声信号処理（ブラインド信号源分離）や脳波・神経活動データなどで実績があり、ガウスノイズを仮定したモデルでは取り出せないシグナルが取り出せる場合がある［20, 21, 22, 23, 24］。デメリットとしては、PCAと同様に符号の曖昧性があること、NMFと同様に大域的最適解が得られる保証が無いこと、また前処理として行われる白色化の影響で、PCAのPC1、PC2のようになんらかの基準（例：分散の大きさ）によって、取り出したパターンを順位づけることが難しいため、どのパターンをより注目すべきか指針を立てづらい点である。

なお、上記の複数の行列分解をかけ合わせることで、互いのデメリットを補うような手法もあり、PCAのように直交性を持たせたNMFやICAとしてOrthogonal NMF［30］、Reconstruction ICA［31］、NMFのように非負値性を持たせたPCAやICAとしてNon-negative PCA［32, 33］、Non-negative ICA［34］といったハイブリットな行列分解手法も提案されている。

References

• [1]  Shi, C. & Yu, P. S. (2017/6/1). Heterogeneous Information Network Analysis and Applications (Data Analytics). Springer, 1007/978-3-319-56212-4
• [2]  Tsuyuzaki, K. & Nikaido, I. (2017/12/24). Biological Systems as Heterogeneous Information Networks: A Mini-review and Perspectives. HeteroNAM'18, arXiv:1712.08865
• [3]  Category: Similarity and distance measures, Wikipedia, https://en.wikipedia.org/wiki/Category:Similarity_and_distance_measures
• [4]  Souza, C. (2010/3/17). Semantic similarity analysis of protein data: assessment with biological features and issues, http://crsouza.com/2010/03/17/kernel-functions-for-machine-learning-applications/
• [5]  Guzzi, P. H. & Mina, M. & Guerra, C. & Cannataro, M. (2011/12/2). Semantic similarity analysis of protein data: assessment with biological features and issues. Briefings in Bioinformatics, 13(5), 569-585. 10.1093/bib/bbr066
• [6]  Sankaran, K. & Holmes, S. P. (2019/8/28). Multitable Methods for Microbiome Data Integration, Frontiers in Genetics, 10(627), 10.3389/fgene.2019.00627
• [7]  Bersanelli, M. & Mosca, E. & Remondini, D. & Giampieri, E. & Sala, C. & Castellani, G. & Milanesi, L. (2016/1/20). Methods for the integration of multi-omics data: mathematical aspects. BMC Bioinformatics, 17(Suppl 2):15, 10.1186/s12859-015-0857-9
• [8]  Li, Y. & Wu, F-X. & Ngom, A. (2016/3/1). A review on machine learning principles for multi-view biological data integration. Briefings in Bioinformatics, 19(2), 325-340. 10.1093/bib/bbw113
• [9]  Gligorijevíc, V & Pržulj, N. (2015/11/6). Methods for biological data integration: perspectives and challenges. Journal of the Royal Society Interface, 12(112):20150571. 10.1098/rsif.2015.0571
• [10]  Meng, C. & Zeleznik, O. A. & Thallinger, G. G. & Kuster, B. & Gholami, A. M. & Culhane, A. G. (2016/3/11). Dimension reduction techniques for the integrative analysis of multi-omics data. Briefings in Bioinformatics, 17(4), 628-641. 10.1093/bib/bbv108
• [11]  Stein-O'Brien, G. L. & Arora, R. & Culhane, A. C. & Favorov, A. V. & Garmire, L. X. & Greene, C. S. & Goff, L. A. & Li, Y. & Ngom, A. & Ochs, M. F. & Xu, Y. & Fertig, E. J. (2018/8/22). Enter the Matrix: Factorization Uncovers Knowledge from Omics. Trends of Genetics, 34(10), 790-805. 10.1016/j.tig.2018.07.003
• [12]  Nguyen, N. D. & Wang, D. (2020/4/2). Multiview learning for understanding functional multiomics, PLOS Computational Biology, 16(4), e1007677. 10.1371/journal.pcbi.1007677
• [13]  Pearson, K. (1901). On lines and planes of closest fit to systems of points in space. Philosophical Magazine, 2(11), 559-72.
• [14]  Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24, 417-41.
• [15]  Lee, D. D. & Seung, H, (1999/10/21). Learning the parts of objects by non-negative matrix factorization. Nature, 401(6755), 788-791. 10.1038/44565
• [16]  Bured, J. J. (2014). Detailed derivation of multiplicative update rules for NMF
• [17]  平岡和幸 & 堀玄. （2004/10/1）. プログラミングのための線形代数
• [18]  金谷健一. （2018/7/28）. 線形代数セミナー: 射影, 特異値分解, 一般逆行列. 共立出版
• [19]  柳井晴夫 & 竹内啓. （2018/9/25）. UP応用数学選書10 射影行列・一般逆行列・特異値分解 新装版. 東京大学出版会
• [20]  Langlois, D. & Chartier, S. & Gosselin, D. (2010), An Introduction to Independent Component Analysis: InfoMax and FastICA algorithms. Tutorials in Quantitative Methods for Psychology, 6(1), 31-38, 10.20982/tqmp.06.1.p031
• [21]  Hyvärinen, A. (2012/12/31). Independent component analysis: recent advances. Philosophical Transactions of the Royal Society. 371(1984), 20110534. 10.1098/rsta.2011.0534
• [22]  Hyvärinen, A. & Oja, E. (2000/7). Independent component analysis: algorithms and applications, Neural Networks, 13(4-5), 411-430. 10.1016/s0893-6080(00)00026-5
• [23]  Aapo Hyvarinen & Erkki Oja & Juha Karhunen & 根本 幾 & 川勝 真喜. （2005/2/10）. 詳細 独立成分分析、東京電気大学出版局
• [24]  戸上真人. (2020/8/24). Pythonで学ぶ音源分離 機械学習実践シリーズ、インプレス
• [25]  Eckart, C. & Young, G. (1936), The approximation of one matrix by another of lower rank. Psychometrika, 1, 211-218, 10.1007/BF02288367
• [26]  佐藤一誠 & 奥村学. （2015/3/13）. トピックモデルによる統計的潜在意味解析 （自然言語処理シリーズ）. コロナ社
• [27]  Madhusudana, S. & Bhiksha, R. & Smaragdis, Paris, S. (2008/05/11). Probabilistic Latent Variable Models as Nonnegative Factorizations. Computational Intelligence and Neuroscience, 2008, 947438. 10.1155/2008/947438
• [28]  Ding, C. & He, X. & Simon, H. D. On the Equivalence of Nonnegative Matrix Factorization and Spectral Clustering. Proceedings of the 2005 SIAM International Conference on Data Mining, 10.1137/1.9781611972757.70
• [29]  Lin, Y. C. & Benner, C. & Mansson, R. & Heinz, S. & Miyazaki, K. & Miyazaki, M. & Chandra, V. & Bossen, C. & Glass, C. K. & Murre, C. (2012/12). Global changes in the nuclear positioning of genes and intra- and interdomain genomic interactions that orchestrate B cell fate. Nature Immunology, 13(12), 1196-204. 10.1038/ni.2432
• [30]  Stražar, M. & Žitnik, M. & Zupan, B. & Ule, J. & Curk, T. (2016/3/15). Orthogonal matrix factorization enables integrative analysis of multiple RNA binding proteins. Bioinformatics, 32(10), 1527-1535. 10.1093/bioinformatics/btw003
• [31]  Le, Q. V. & Karpenko, A. & Ngiam, J. & Ng, A. Y. (2015/7). ICA with Reconstruction Cost for Efficient Overcomplete Feature Learning. NIPS'11 Proceedings, 1017-1025.
• [32]  Allen, G. I. & Maletić-Savatić, M. (2011/11/1). Sparse non-negative generalized PCA with applications to metabolomics. Bioinformatics, 27(21), 3029-3035. 10.1093/bioinformatics/btr522
• [33]  Asteris, M. & Papailiopoulos, D. S. & Dimakis, A. G. (2014). Nonnegative Sparse PCA with Provable Guarantees. Proceedings of 31th ICML PMLR, 32(2), 1728-1736
• [34]  Plumbley, M. D. (2004/3). Algorithms for nonnegative independent component analysis. IEEE Transactions on Neural Networks, 14(3), 534-543, 10.1109/TNN.2003.810616

略語リスト

・HINs

Heterogeneous Information Networks

・PCA

Principal Component Analysis

・NMF

Non-negative Matrix Factorization

・ICA

Independent Component Analysis

・EVD

Eigen Value Decomposition

・SVD

Singular Value Decomposition

・MU則

Multiplicative Update Rule

著者略歴

露崎 弘毅 2015年、東京理科大学生命創薬科学科博士後期課程終了。博士（薬科学）。同年より、理化学研究所情報基盤センターバイオインフォマティクス研究開発ユニット（現在の所属1）に在籍。現在、基礎科学特別研究員及びJSTさきがけ研究員を兼任。個人としては、世界で最もBioconductorにRパッケージを登録している。（1細胞）トランスクリプトームデータを中心に、複数のデータを統合する解析手法の開発に取り組んでいる。テンソル分解の執筆・講演依頼が多く、テンソル芸人としての地位を確立しつつある。趣味はサーフィン、バイク、料理。 ホームページ：https://sites.google.com/view/kokitsuyuzaki