2024 年 40 巻 2 号 p. 58-82
2024 年 40 巻 2 号 p. 58-82
The model proposed by Henrich (2004), which is often cited as a theoretical basis for understanding the role of demography in the cumulative cultural evolution of technology, is expounded for general readers and reanalyzed through a novel approach based on the concept of innovation rate. In this analysis, the model is generalized to allow a broader class of distributions for the distribution of individual skill levels, while preceding studies explored only the cases of Gumbel, logistic, and normal distributions. It is revealed that the expected number of innovators per generation is a key determinant of the sign and tempo of technological growth. In particular, the maximum skill level in a population grows cumulatively when the expected number of innovators per generation exceeds a certain threshold. Based on the results of the theoretical discussion, existing experimental tests of the model and related demographic hypotheses are reevaluated in the latter half of the article, while remarks are made on future possible tests of the model from a quantitative perspective.
ヒトは文化的な動物である。この単一種の陸上哺乳類が成し遂げた広範な環境における分布拡大の背景にあるのは,文化的に伝達され改良されていくさまざまな生業の技術であり,その多種多様に分岐・融合する文化的系譜の終端の一つに近代社会の文明と科学技術がある。ヒトは,模倣学習によって世代から世代へ技術を受け継いでいく過程で,幾重にもわたって改良を積み重ね,個人学習だけでは到達することが不可能なほど複雑で高度な技術を生み出すことができる。このようなプロセスは「累積的文化進化」と呼ばれる(Boyd & Richerson, 1996)。多くの研究者が,累積的文化進化の存在をヒトの著しい特徴であるとし,それが多様な環境への適応において決定的な役割を果たしてきたと論じている(Boyd & Richerson, 1996; Henrich, 2016 今西訳 2019; Laland, 2017 豊川訳 2023; Richerson & Boyd, 2006; Tomasello, 1999 大堀他訳 2006)。したがって,技術の累積的文化進化のプロセスを理解することは,文化進化研究の興味深い一トピックであるに留まらず,人類の適応の本質を理解し,集団としての持続的発展の可能性を考察するための重要な学際的テーマでもある。これまで数多くの理論・実証研究がこの研究テーマに捧げられてきた。特に理論研究では,Henrich(2004)による数理モデルが一つのランドマークとなっており,それ以降に発表された理論・実証研究の双方に多大な影響をもたらしている。Henrich(2004)を発端として,複数の数理モデルが派生モデルあるいは代替モデルとして提案されただけでなく(Aoki, 2018; Baldini, 2015; Bentley & O’Brien, 2011; Kobayashi & Aoki, 2012; Kobayashi et al., 2016; Mesoudi, 2011; Powell et al., 2009; Vaesen, 2012),モデルの検証のために数多くの実証研究や観察に基づく論証が行われ,肯定的あるいは否定的見解を示す研究者たちの間で論争が繰り広げられてきた(Caldwell & Millen, 2010; Collard, Buchanan et al. 2013; Collard et al., 2005, 2011, 2016; Derex et al., 2013; Fay et al., 2019; Kempe & Mesoudi, 2014; Kline & Boyd, 2010; Muthukrishna et al., 2014; Read, 2006; Vaesen et al., 2016)。このような経緯もあり,Henrich(2004)の数理モデルは,ヒトの文化的適応や技術の文化進化を語るうえで,避けては通れないものになっている。本稿では,こうした多大な影響力を発揮してきたHenrich(2004)の数理モデルについて解説し,なおかつ実証研究による当該モデルの検証について,既存研究の評価を交えつつ将来的展望を述べる。
上記の目的は,「数理モデル」および「実証研究」と題した二つの章を通じて達成される。まず「数理モデル」の章では,必ずしも理論を専門としない読者に向けて,Henrich(2004)のモデル(以降Henrichモデル)の詳細な仕組みと本質について解説する。Henrichモデルは,Shennan(2001)の理論研究と並び,技術の累積的進化の様相を決定する要因として最も重要なものは人口や集団構造などといった集団の人口学的な特性であるとする,いわゆる「人口仮説」の論拠をなす数理モデルである。Henrichモデルを学ぶにあたり,原著であるHenrich(2004)による解説は洗練されておらずわかりにくいため,初学者にはあまりお勧めしない。一方でKobayashi & Aoki(2012)による同モデルの解説は比較的成熟した段階にあるため数学的な明快さは改善されているが,理論誌に掲載されていることから,一般の読者にとっては細部や基礎的部分の説明が不親切で敷居が高い。本稿ではこうしたギャップを埋めると同時に,既存研究ではほとんど検討されなかった定量的検証という目標に即し,「イノベーション率」という概念に焦点を当てた新しい方法でモデルの分析を展開する。この方法は直感的にわかりやすいという便益をもたらすだけでなく,ある側面で既存研究の一般化を可能にする。この新たなアプローチを通して得られた結果に基づき,筆者は,Henrichの提唱した人口仮説のメカニズムを理解するうえで,個人の技術がどのような生物学的プロセスを経て獲得され,その水準がどのような分布に従うかといった詳細は,必ずしも必要とされないと論じたい。この主張は,続く第3章(特に「伝達様式」の節)において,モデルの検証方法や,モデルに対する批判の妥当性について論じる際に,理論的な立脚点としての役割を担うことになる。なお,文化進化の数理モデル一般に関する日本語の文献としては,田村(2020)が優れている。その内容は数学的ではあるが,説明は概して平易であり,Henrichモデルの概説もなされている。本稿でも,特殊な数学的知識は仮定しないで議論を進めるが,他で手に入る解説との差別化を図るためにも,数学的導出に関してはできるだけ省略しないようにした。結果として,実証研究者だけでなく,これから同分野の理論研究を志す学生にとっても,日本語で読める手頃な参考文献になることを期待している。
人口仮説に関連する数理モデルには,Henrichモデルの他にも異なるアプローチが存在する。その中でもおそらく重要なのは,Strimling et al.(2009)が導入し,青木健一をはじめとする日本人研究者らによって発展させられてきた,0,1ベクトルモデルと呼ばれる枠組みである(Aoki, 2018; Nakamura et al., 2020; Strimling et al., 2009)。0,1ベクトルモデルも人口仮説を考えるうえで決して無視はできないが,その詳細はHenrichモデルよりも奥が深く,本稿では扱いきれないため,適宜必要な結果だけを紹介することにした。興味がある方は,古い文献よりも,むしろ理論が洗練されている最近の関連業績から読み始めてみるとよい(Aoki, 2018; Nakamura et al., 2020など)。
続いて「実証研究」の章では,実験室あるいはオンライン実験によるHenrichモデルの定量的検証の可能性について前章で展開された理論に基づく展望を述べる。ここでいう定量的検証とは,何らかの量的変数について,モデルによる予測とデータからの算出がおおむね一致することを確認する手続きを指す。Henrichモデルに限らず,文化進化の数理モデルはその多くが抽象度の高いものである。そのためか,個人的所感では,モデルを作った本人だけでなく,そのモデルを検証しようとしている実証研究者も,定量的検証については最初から念頭にない場合が多いように思われる。この点は,集団遺伝学や伝統的な進化の理論研究が定量的検証において成功を収めてきたことと対照的である。集団遺伝学において用いられる数理モデルは総じて抽象度が高いものばかりであるが,さまざまな工夫により定量的検証に耐え,理論と実証の緊密な連携を実現している。また進化生態学においても,例えば最適性比の研究では,進化ゲーム理論に基づく数理モデルの定量的実証研究が著しく成功している。社会科学の一分野としても,この点で文化進化研究は遅れている感がある。経済学では,実験で得られたデータと伝統的ゲーム理論の予測の間の定量的ずれから理論の不備を特定することで,理論が日々修正,発展させられている。それに比べると,文化進化の分野では,データによる定性的検証によってモデルが支持されたかに見えても,あれやこれやの水掛け論が展開され,同じ場所で足踏みをして中々前進しない感がある。
遺伝子と違って文化は離散的実体を持たない場合が多いので,その分現実との定量的比較に耐え得るモデルを作るのはより困難である。しかし,その困難さと比較しても,定量的検証から得られる恩恵は大きいと思われる。定性的検証は,多くの場合モデルの前提と定性的予測の,データを用いた反証という形式をとるため,モデルがデータによって反証できなかった(すなわち支持された)場合,「前提と予測が一致しただけで,背後のメカニズムは理論の想定したものと異なるのではないか」という反論の余地が残りやすい。定量的検証の一つの強みは,予測と結果が定性的な一致を見た場合でも,それらの間の定量的なずれから,理論の間違いや考慮しなかった要因に気づくことができるというところであり,定性的な検証よりも建設的な考察が可能なところである。
モデルと現実の乖離は,実験研究の場合,実験側の設定をモデルに近づけることによっても埋めることができるのであり,これが実験研究の一つの魅力である。本稿の後半では,Henrichモデルという抽象的なモデルを題材とし,計算や実験設定を工夫したりすることで,モデルと実験の乖離を減らして定量的検証に繋げられるか考察する。その際に,課題となる事項を洗い出すことで,当該研究分野の発展に貢献することを狙う。同時に,こうした定量的検証に関する考察から,既存研究に内在する課題を浮き彫りにできることも具体な研究の例とともに示したい。
なおHenrichモデルは,社会科学や生物学の広範な分野に対して学際的な影響を持つが,本稿では主要な読者として実験や理論に興味のある方々を想定している。したがって,野外の実証研究については必要に応じて言及する程度に留め,詳細には深入りしないことにする。
当初Henrichモデルは,タスマニア原住民の集団における技術文化の喪失を説明するための数理モデルとして導入された(Henrich, 2004)。タスマニアは,およそ7万~1万年前まで続いた氷河期の間,オーストラリア大陸と地続きであり,その間に大陸からの人類の移入と定着が起きた。しかしながら,最終氷期の終了とともに大陸との間にバス海峡が形成され,大陸の集団から分断された。有史になってから西洋の探検隊がタスマニア原住民を発見した時点で,タスマニア集団には最近隣の大陸集団に比べてはるかに貧困な道具文化しか残存していなかったと言われている。Henrichはこれをタスマニア集団における技術的な衰退ととらえ,その原因が大陸からの断絶による人口縮小にあると論じ,その因果関係を説明するための数理モデルを導入した。
Henrich(2004)以降,この数理モデルとその背後にあるメカニズムは技術の累積的文化進化に関わるいくつかの他の事例を説明するための拠り所として援用されるとともに,データを用いた検証・反証が試みられている。Read(2006)のように,タスマニアの事例への応用そのものについて疑問を呈する研究者もいる。他の応用事例として最も有名なものの一つは,Powell et al.(2009)による現代人的行動の出現と集団サイズの関係を扱った研究である。この研究で著者らは,Henrich(2004)のモデルに立脚し,後期旧石器時代における現代人的行動の出現の主要な決定要因が人口の増加であるとする説を打ち立てた。しかし,この主張に対しては理論・観察の両側面から疑問視する研究者も多い(Collard, Buchanan et al., 2013; Collard et al., 2016; Vaesen, 2012; Vaesen et al., 2016)。これらの個別研究を含む,集団の人口学的属性が技術の累積的文化進化の主要な決定要因であるとする考え方の全体を,本稿では慣例にならい「人口仮説」と呼ぶことにする。技術の累積的文化進化の決定要因に関する代表的な仮説には,人口仮説の他に,「住居移動性仮説」,「資源タイプ仮説」,「環境リスク仮説」があるが,人口仮説はそれらの中で最も激しい論争を巻き起こしてきた仮説である(Strassberg & Creanza, 2021)。
定量的データを用いて人口仮説を検証した研究(数理モデルそのものの定量的検証ではなく,あくまで定量的データを用いて数理モデルの予測を定性的に検証したもの)としては,Kline & Boyd(2010)が行ったオセアニア島嶼集団における道具の多様性に関する研究が有名である。この研究で著者らは,オセアニアに存在する10の島嶼集団において,生業に活用されている道具の種類の数や道具あたりの構成部品(テクノユニット)の数が集団のサイズと正の相関を持つことを示し,人口仮説を支持する証拠であると主張した。この結果は,のちにデータセットを拡大した同様の分析によっても再び支持されている(Collard, Ruttle et al., 2013)。しかし一方で,こうした正の相関は,農耕や牧畜を営む生産型社会においてのみ観察されることも明らかにされた。採集型社会においてはこのような相関は検出されず,むしろ環境要因と道具の多様性が相関を示すことが知られている(Collard, Buchanan et al., 2013; Collard et al., 2005, 2011; Fogarty & Creanza, 2017; Read, 2006)。この原因については諸説あるが,筆者の考えでは未解決の問題であり,挑戦する価値のある重要なトピックである。人口仮説の実験による実証研究も複数行われており,仮説を支持する結果(Derex et al., 2013; Kempe & Mesoudi, 2014; Muthukrishna et al., 2014)と支持しない結果(Caldwell & Millen, 2010; Fay et al., 2019)がともに得られている。いずれもHenrichモデルを検証したというよりは,人口仮説一般の定性的予測である人口と技術水準の正の相関を検出しようとしたものであり,結果が仮説を支持した場合でも,背後のメカニズムがHenrichモデルと異なるものも含まれている(Kempe & Mesoudi, 2014)。
仮定従来のHenrichモデルでは,他集団から完全に独立した仮想的な単一集団を想定する。集団のサイズ(すなわち人口)は時間的に不変であり,変数Nで表される。世代更新は,いわゆる同期更新(synchronous updating)あるいは離散世代(discrete generations)と呼ばれる方式で行われる。つまり,時間は非負の整数(0,1,2,3,…)で表され,1ステップ時間が進むごとに,すべての個体が次世代個体にとって替わられる。したがって,1タイムステップが1世代に相当する。もちろん現実の人類では,集団サイズは一定ではないし,世代も離散的ではない。しかしながら,文化進化の理論研究では,ほぼ常にこういった大胆な単純化が行われることを最初に断っておく。ちなみにHenrich自身は,Nを「有効な社会学習者数」としており,集団の成員が他集団と頻繁に交流する場合には,Nは集団の実際の個体数よりも遥かに大きな値を取り得るとしている。しかしながら,筆者に言わせれば,「有効な社会学習者数」というような曖昧な概念はモデルの初学者を困惑させるだけでなく,悪い意味であらゆる反証に対する万能の言い訳として機能し得るので,理論・実証の両側面で益がないように思われる。少なくともモデルを構築する際は,閉じた集団の実際の成員数であると定義したほうが明快であるし,本稿でもそうする。また,Henrichは,異なる時点の集団は必ずしも異なる世代を表さず,同じ世代内の異なる時点の状態を表してもよいと言っているが,このような拡大解釈はモデルの構造上やや無理があるように思うので,本稿では採用しないでおく(ただし実験において,同じ被験者が,異なる世代として繰り返し動員される場合についてはこの限りではない)。
集団中のN個体は各々,記号zで表される実数値を与えられており,これが個人の有する技術の水準を表すとする。技術水準は,Henrich自身の言によれば,矢柄の真直度のような単一の技能の卓越度を表してもよいし,所有する技術レパートリーの大きさを表してもよいとしている。技術水準zが具体的に何を表すかということは,Henrichモデルにまつわる論争においては争点の一つであるし,本稿の重要な論点でもあるので,以降でも折に触れて考察するが,ここではいったん,zが大きい個体ほど技術的に優れているという説明に留めさせていただきたい。ただし,本稿では一貫して,zは実際に測定可能なものであるという立場を採用することをあらかじめ断っておく。
世代更新に伴い,次世代の個体の各々は,現世代の個体たちの中から,最も技術的に優れた個体,すなわち最もzの大きな個体を選択し,その技術を模倣しようとする。しかしながら,学習には必ずエラーが伴い,次世代個体のz値は模倣対象のz値とは同じにならず,多くの場合模倣対象よりも小さな値になる。より具体的には,Henrichは各次世代個体のz値が,各々独立に同一のガンベル分布に従って確率的にばらつくと仮定した。彼はまた,分布に関する仮定の特殊性が与える影響を評価するため,z値がロジスティック分布に従う場合についても分析を行っている。ちなみに,Vaesen(2012)は,Bentley & O’Brien(2011)によるHenrichモデルに対する批判を受けて正規分布の場合について同様の分析を行い,Henrichの結論の頑健性を確認している。
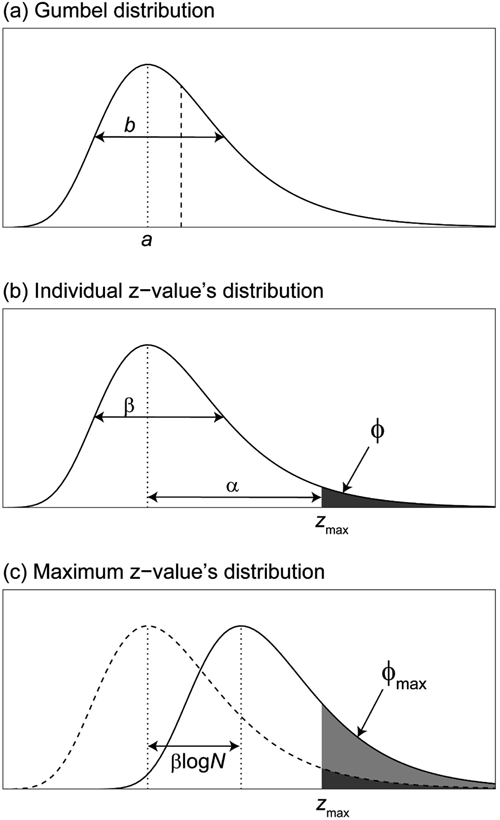
さて,現世代の最高の技術水準をzmaxで表すことにしよう。次世代に現れる個体の大多数はzmaxを超えることができないが,それでも,Nが大きければ,まれにではあるがzmaxを超える技術水準を手に入れるものが現れる。そしてその確率はNが大きいほど大きくなるはずである。このことを理解するのに,ガンベル分布の知識は必要ない。まず,エラーの生じ方が個体の間で異なってはいないとすると,学習後の技術水準がzmaxを超える確率は個体によらないので,それを共通の記号ϕで表すことができる。これをKobayashi & Aoki(2012)にならい「イノベーション率」,あるいは後で定義する集団のイノベーション率と区別したい場合は個人のイノベーション率と呼ぶことにする。イノベーション率の優れた点は,その具体性と一般性である。現実とモデルの直接の対応付けが必要とされる定量的検証においてこの性質は有用であるが,既存研究ではイノベーション率についてあまり掘り下げた議論がなされていない。そこで本稿では,Henrichモデルの解説を行うにあたって,イノベーション率を中心とした議論を展開することで,これまでとは少し異なる角度からモデルのふるまいを観察してみよう。
さて,次世代の中に少なくとも一人zmaxを超える技術水準を手に入れる個体が現れる確率ϕmaxは,(各々の個体の学習が独立であるという仮定を用いれば)全くそういった個体が現れない確率(1−ϕ)Nを1から引くことで得られるので,
 | (1) |
で与えられることがわかる。本稿ではこれを集団のイノベーション率と呼ぶことにする。上式より,集団のイノベーション率ϕmaxは,個人のイノベーション率ϕが人口Nに依存しないならば,(1−ϕ<1であることから)人口Nが大きいほど大きくなる。このような人口の効果によって,大きな集団ほど,1世代の技術伝達を経たのちに技術の最高水準が改善している確率が高くなるという結論が導かれる。
次世代のN個体分のz値が確定されると,離散世代の仮定より,不要になった現世代は消滅し,次世代によって置き換えられる。つまり次世代が新たな現世代となる。あとは上記で定義された過程が繰り返されるのみである。すなわち,新たな世代の技術水準が,各々独立な学習過程を経て決定され,その後既存世代を置き換える。式(1)によって得られた結論を外挿することにより,個人のイノベーション率が経時的に一定でありさえすれば,複数世代を経たのちに現在に比べて技術の最高水準が高まっている確率もまた,人口とともに増大すると推測される。直観的にはそのように思われるし,ほとんどの事例でその予測は正しいだろう。ただし,数学的にはこの主張は自明ではないように思われる。なぜならば,遠い将来に技術の最大水準がどこにあるかということは,イノベーション率ϕだけでなく各世代における個人の技術水準が従う理論分布の詳細に依存するからである。筆者の記憶では,Henrichモデルに関して,この問題をまともに取り上げた文献はない。おそらく個別の事例でこの予測を確認するには,シミュレーションに頼るのが賢明かもしれない。
正の技術成長の条件上では,Henrichモデルの概要を説明し,そこで集団の技術水準(の最高値)が一世代経過後に初期状態よりも高まっている確率が人口にどのように依存しているかを示した。ここでは,もう少し突っ込んで,集団の技術水準が時間とともに上昇すると期待されるのか,それとも逆に下降すると期待されるのか(もう少し具体的に言うと,一定時間後の集団の技術水準の最大値の期待値が,現在の技術水準の最大値よりも大きいのか否か)について,イノベーション率ϕと人口Nから予測を試みる。
いきなり複数世代を考えると難しいので,まずは一世代の変化に注目しよう。ここでの目的は,一世代経過後に,次世代集団の最大の技術水準の期待値が,現世代集団の最大の技術水準zmaxよりも大きくなる条件を求めることである。しかしながら,この条件を求めるためには,二つの予備知識が必要であるので,先にそれらについて説明しよう。
まず,第一の予備知識として,次世代の各個人の技術水準の期待値が,現世代の最大水準zmaxよりも大きくなる条件を明確にしておこう。本稿ではこの条件を,イノベーション率ϕの言葉で表現しておきたいのだが,そのためには,以下で説明する「期待値超過率」という量を定義しておくと便利である。次世代の個人が学習を行う際に,結果として獲得される技術水準(z値)がどのような分布に従うとしても,その期待値さえ存在していれば,「技術水準がそれ自身の期待値より大きくなる確率」が定義できかつ計算できることに注意してほしい。正規分布やロジスティック分布のような左右対称な分布ならば,期待値と中央値が一致するので,その確率は0.5であるが,非対称な分布では一般にそうはならない。例えば指数分布であれば,その確率は約0.368(ネイピア数eの逆数)であり(証明略),ガンベル分布であれば約0.430(証明は後述)である。この確率を,本稿では便宜上「期待値超過率」と呼ぶことにする。Figure 1では,正規分布,指数分布,ガンベル分布,ロジスティック分布の確率密度関数を示しており,垂直の点線で示された期待値よりも右側の着色された部分の面積が期待値超過率を表す。期待値超過率は一般には分布のパラメータ(期待値や標準偏差)に依存するが,ここに挙げた4種の分布に関しては,パラメータに依存せず一つの実数に定まる。さて,イノベーション率は,次世代の個人の技術水準が現世代集団の最高水準zmaxを上回る確率であるから,zmaxよりも右側の濃い色で着色された部分の面積で与えられる。Figure 1より,学習者の技術水準の期待値がzmaxを上回るということ(つまり垂直の点線がzmaxより右側に位置すること)と,イノベーション率が期待値超過率を上回るということは全く同じことであることがわかる。つまりイノベーション率が期待値超過率を上回るとき,そのときに限り,次世代の各個体の技術水準の期待値は現世代の最大水準zmaxを上回る。

注)垂直の破線が期待値であり,それより右側の着色された部分(薄い灰色,濃い灰色の両方)の全面積が期待値超過率(それぞれ(a)0.5,(b)約0.368,(c)約0.430,(d)0.5)を与える。(a~d)を次世代の個人の分布として見たとき,現世代の最大技術水準はzmaxで表されており,それより右側の濃い灰色の部分の面積がイノベーション率ϕを与える。
第二の予備知識は,次世代集団の最大技術水準が,多くの場合,近似的にガンベル分布に従う確率変数であると考えてよいということである。次世代の各個人の技術水準が確率変数である以上,次世代集団の最大技術水準もまた一つの確率変数であり,その分布の形状は,一般には個人の技術水準の分布の形状に依存している。ところが,後述するように,次世代の各個体の技術水準が従う分布が,正規分布,対数正規分布,指数分布などを含む,ある広い分布の族に属し,なおかつ次世代個体数Nが十分に大きければ,次世代の最大の技術水準は近似的にガンベル分布に従う。後ほど詳しく解説するが,このような確率分布の性質が成立するとき,一般に極値理論の専門用語で,「分布がガンベルの吸引域に属する」と表現する(西郷・有本,2020)。ちなみに,Henrich(2004)やVaesen(2012)が用いたガンベル分布,ロジスティック分布,正規分布はすべてガンベルの吸引域に属する。通常は,次世代の最大技術水準がガンベル分布に従うということはあくまで近似的にのみ成立するものであり,しかも,Nが大きいという条件が必要とされる。ただし,個人の技術水準がガンベル分布に従う場合に限っては,例外的に,任意のNについて,次世代の最大技術水準は厳密にガンベル分布に従う(これをガンベル分布の最大値安定性と呼ぶ)。個人の技術水準の分布によっては,次世代の最大の技術水準の分布がガンベル分布で近似できない場合もあるが,そのような場合については,別途考察することにし(次章,「技術水準の測定方法」の節を参照),さしあたっては次世代の最大技術水準が近似的にガンベル分布に従うと想定する。
これで必要な予備知識がそろったので,いよいよ本題に戻り,次世代集団の最大の技術水準の期待値が現世代集団の最大技術水準zmaxを上回る条件を求めることにしよう。第二の予備知識によれば,次世代の最大技術水準はそれ自体が一つの確率変数であり,近似的にガンベル分布に従う。したがって,その密度関数はFigure 1(c)のような形をしているはずである。そして,そのようにFigure 1(c)を,次世代の一個人の技術水準の分布ではなく,次世代集団の最大技術水準の分布であると解釈すると,zmaxより右側の濃い灰色で着色された部分の面積は,個人のイノベーション率ϕではなく,集団のイノベーション率ϕmaxを与えることに注意されたい。さらに,第一の予備知識によれば,イノベーション率ϕが期待値超過率を上回るとき,そのときに限り,次世代の各個体の技術水準の期待値は現世代の最大水準zmaxを上回ることを思い出そう。Figure 1(c)より,同じ論法が,次世代集団の最大値にも適用できることが明らかである。すなわち,集団イノベーション率ϕmax(濃い灰色部分の面積)が,ガンベル分布の期待値超過率(着色部分の全面積)を上回るとき,そのときに限り,次世代集団の最大技術水準の期待値は,現世代の最大水準zmaxを上回ることがわかる。そしてガンベル分布の期待値超過率は,すでに述べたように,分布のパラメータによらず約0.43である。したがって,上の議論を用いれば,集団イノベーション率(1)が0.43を上回れば,次世代の最大の技術水準は現世代のそれを上回ることが期待される。この条件は,式(1)より,(1−ϕ)Nが0.57(=1−0.43)より小さくなるということに等しい。ここから,たとえ個人のイノベーション率ϕが個人の期待値超過率を下回っていて,それゆえ各個人はzmaxを超えられないと期待される場合でも,集団が十分に大きければ,集団中の最大の技術水準については,次世代が現世代を超えることが期待される。では,どのくらい人口が大きければそれが期待されるのかを知るためには,条件(1−ϕ)N<0.57を変形すればよい。両辺の対数をとってlog(1−ϕ)で割ることにより(1−ϕ<1よりlog(1−ϕ)<0であるから,不等号の向きが変わることに注意),
 | (2) |
ここで,log0.57≈−0.562である事実を用いた。この式は少しわかりづらいが,右辺はイノベーション率ϕの減少関数であり,ϕが0に近づくとき無限大に発散する。したがって,個人のイノベーション率が小さいほど,正の技術成長に必要な集団サイズは大きくなる。具体例として,個人のイノベーション率が0.1パーセント(ϕ=0.001)であれば,右辺は小数点以下切り捨てで561であるので,562人以上の集団であれば,集団の最大技術水準は1世代後に増加していることが期待される(もちろん実現値は期待値の周りで一定の広がりをもってばらつく)。後で,式(2)とほとんど同じ結果を与えるもっとわかりやすい近似式(4)を与えるので,式(2)がわかりにくいと感じる読者は,そちらを見ることをお勧めする。
次に上記の議論が複数世代に外挿できるかどうか考察しよう。最も単純な場合として,2世代後に最大技術水準の期待値が現在の最大技術水準よりも大きくなる条件を考えることにする。現在の最大技術水準をZmax,0,1世代後をZmax,1,2世代後をZmax,2で表すことにしよう。また,確率変数の期待値を記号E[⋅]で表すことにする。すると,2世代後と現在の差異の期待値は簡単な式変形より,
 | (3) |
と書ける。最右辺の2項めは0世代から1世代への増分の期待値であり,1項めは1世代から2世代への増分の期待値である。これらはどちらも,条件(2)が満たされるかどうかで正負が決まるので,Nとϕが一定ならば,両項は正負の符号が等しい。よって,2世代後の期待値が現在よりも大きいかどうかの条件は,やはり1世代の場合と同じ条件式(2)で与えられる。全く同様に,任意の世代数を経過したのちの最大技術水準の期待値が現在のそれよりも増加している条件も,(2)で与えられることがわかる。ここで,もちろんϕは経時的に一定でなくてはならないが,それさえ満たしていれば,個人の技術の分布の形状は時間とともに変化しても構わないことに注意してほしい。例えば,時間とともに技術水準の分布の分散が次第に減少したり増加したりしてもよい。
Henrich(2004)の式(3)(同様にKobayashi & Aoki(2012)の式(8b)やBentley & O’Brien(2011)の式(7))は,上式(2)の特殊な場合であり,個人の技術水準がガンベル分布に従う場合に対応している(実際には,彼らの制約はもう少し強く,標準偏差の経時的な不変性を仮定している)。この特殊な場合に限り,式(2)は近似的にではなく,厳密に正しい。それ以外の場合,例えば個人の技術水準が正規分布に従う場合などは,Nが十分大きいときでないと条件式(2)が適用できない。なぜならば,式(2)を導くにあたって,次世代集団の最大技術水準がガンベル分布に従うという前提を用いたが,この前提は,上で「第二の予備知識」として説明したように,個人の技術水準がガンベル分布に従うか(この場合は,最大値安定性より任意のNについて厳密に前提が成り立つ),もしくはその分布がガンベルの吸引域にあってなおかつNが大きいときに成立する(この場合は近似的にのみ成立する)前提だからである。ところで,式(2)の右辺はϕの減少関数であって,しかもϕが0に近づくとき無限大に発散する。そのため,ϕが小さければ,それに連動して閾値となるNの値は大きくなる。したがって,式(2)の適用にあたってNが十分に大きい必要があるということは,ϕが十分に小さい必要があることを意味する。しかしながら,この制約は少なくとも野外で一般的にみられる技術に関する限り,それほど問題にならないと思われる。なぜなら,個人のイノベーション率が小さいというのは,現実にありそうなことだからである。また,ϕが小さいならばlog(1−ϕ)は−ϕとほとんど同じ値をとるので,次の式も,ほとんど同じくらい正確な閾値を与えるだろうし,こちらのほうが直観的で計算も簡便である。
 | (4) |
逆に,ある一定の人口Nが与えられたときに,長期的に見て正の技術成長が起きるには,個人がどれくらいの確率でイノベーションしなくてはならないかという問題についても,式(4)を次のように変形すれば答えることができる。
 | (5) |
この式から,例えば1,000人の集団では,少なくとも0.056パーセント程度のイノベーション率を各個人に確保しなくてはならないことがわかる。さもないと集団は技術的に衰退してしまうだろう。また,自明な式変形だが,以下の不等式も示唆に富む。
 | (6) |
この式の左辺Nϕは世代あたりイノベーター数(の期待値)という明確な解釈を持っている。すなわち,集団が持続的に技術的に発展していくためには,人口によらず,平均して1世代ごとに約0.562人のイノベーターを創出する必要がある。そのためには,個人が十分創造的であるか(ϕが大きい),もしくは母体となる集団が十分大きい(Nが大きい)必要がある。
Figure 2は,個人の分布がFigure 1(a)のような標準偏差σ=1の正規分布に従うと仮定し,イノベーション率をϕ=0.001に固定したうえで,5通りの集団サイズ(N=200, 400, 600, 800, 1,000)に対してシミュレーションを行った結果を表している。このシミュレーションにおいて,次世代の個人の技術水準が従う理論分布の最頻値の位置は,イノベーション率と標準偏差がともに一定であるため,現世代の最大値zmaxに依存して増減することに注意してほしい。イノベーション率がϕ=0.001であるので,式(4)より,技術成長の正負が切り替わる集団サイズの閾値はおよそ562である。Figure 2からわかるように,予測通り閾値562よりも大きい集団サイズ(N=800, 1,000)では最大・平均技術水準ともに正の成長を示しており,逆に閾値よりも小さい集団サイズ(N=200, 400)では最大・平均技術水準ともに負の成長(衰退)を示している。また,閾値付近の個体数(N=600)では,成長速度はほぼ0であり,最大・平均技術ともに横ばいになっていることがわかる。

注)5通りの集団サイズ(N=200, 400, 600, 800, 1,000)に対して1回ずつシミュレーションを行い,全5回分の結果を同時に図示した。個人の技術水準は標準偏差σ=1の正規分布(Figure 1(a))に従うと仮定し,イノベーション率はϕ=0.001で一定,初期状態では全構成員の水準が0であると仮定した。
一方,Figure 3は,個人の技術水準の分布が,正規分布,指数分布,ガンベル分布,ロジスティック分布に従うとした4通りの場合について,シミュレーションを行って人口Nが10世代後の最大技術水準に与える影響を調べた結果である。ただし,このうち指数分布以外は,パラメータを二つ持つため(例えば正規分布なら期待値と標準偏差),イノベーション率ϕが一定であるという仮定のみからは個人の分布は一意に定められない。そこで,各々,分布の分散が(よって標準偏差も)時間的に不変であると仮定した。また,Figure 3の各点は100回の繰り返しを行って平均をとったものであることに注意されたい。初期の技術水準はすべての個体で等しいと仮定し,その値はFigure 3中の水平の実線で示されている。イノベーション率については三つの値,ϕ=0.005, 0.001, 0.0005を用いた。これらのイノベーション率に対しては,式(4)によれば,技術成長の符号が正に転じる人口Nの閾値はそれぞれおよそ112, 562, 1,124となる。Figure 3からわかるように,個人の分布によらず,おおむね人口Nが理論的に予測された閾値を超えるときに技術が正の成長に転じている。

注)個人のイノベーション率はϕ=0.005(△),0.001 (■),0.0005(●)を仮定し,個人の技術水準は(a)標準偏差σ=1の正規分布,(b)指数分布,(c)標準偏差 のガンベル分布,(d)標準偏差
のガンベル分布,(d)標準偏差 のロジスティック分布に従うとした。各点は同じパラメータ値で100回のシミュレーションを行い平均をとったものである。初期状態ではすべての個体の技術水準が等しく,その値は(a),(c),(d)ではz=0,(b)ではz=1とした。(b)のグラフにおいて縦軸は対数軸であることに注意。
のロジスティック分布に従うとした。各点は同じパラメータ値で100回のシミュレーションを行い平均をとったものである。初期状態ではすべての個体の技術水準が等しく,その値は(a),(c),(d)ではz=0,(b)ではz=1とした。(b)のグラフにおいて縦軸は対数軸であることに注意。
条件式(4–6)を用いると,例えば人口衰退がもたらす帰結について,有用な洞察を得ることができる。人口が減衰して例えば現在の半分になったとすると,正の技術成長に必要な個人のイノベーション率は現在の倍になる。そのため社会は益々大きな教育投資を必要とし,それは繁殖開始時期の遅延や産子数の低下などといった繁殖上のコストとなって現れ,さらに人口の減衰を加速してしまうかもしれない。正の技術成長が起きるためには世代あたりイノベーター数Nϕを0.562よりも大きい値に維持しなくてはならないが,上の議論によればNとϕにはトレードオフがある可能性がある。Mesoudi(2011)が想定したように,技術が発展するほど習得が難しくなってϕを下げる圧力が働くとすれば,社会はそれに対抗してϕを押し上げるためにNを犠牲にしなくてはならない可能性がある。したがって,世代あたりイノベーター数を0.562以上にキープすることが次第に難しくなっていき,それが0.562に一致するあたりで技術発展が止まるであろう。このような技術停滞を回避するには,Nとϕのトレードオフが起きないような社会を実現し,なおかつNが際限なく増えていけるように常に資源の拡大を行うことが必要になるであろう。ところが,人口Nを増加させるための資源の拡大は,それ自体,新規エネルギー源の開発などのための技術の発展に依存している。したがって,もしそういった資源開拓の技術が十分に発展する前にNϕが0.562まで低下してしまったら,資源開拓のための技術発展も人口増加もともにストップしてしまう。しかし,もし技術発展のための努力がN増加(あるいはϕ増加)のための技術に集中的に投入されることで,Nϕを0.562より大きい値にキープできるならば,人口と技術はともに際限のない正の成長を示すことが可能かもしれない。ただし,これらの議論は,離散世代をはじめとするさまざまな単純化を施したモデルから導かれるものであるので,注意が必要である。実際,Kobayashi & Aoki(2012)が示したように,世代の重複を許したモデルは,離散世代モデルとかなり異なった挙動を示す。また,書籍やコンピュータなどの各種外部記憶媒体の存在は重複世代と似たような効果をもたらすだろう。なお,集団の技術水準と人口の間に相互のフィードバックがある場合の技術の累積的文化進化に関しては,Aoki(2018)が本格的な理論的分析を行っているので,興味がある方はそちらを一読されたい。
標準化された技術成長速度上では,技術発展の速度が短期・長期的に正の値をとる条件を求め,人口が個人のイノベーション率の関数として与えられる特定の閾値より大きいときに条件が満たされることが示された。さらに,もう少し踏み込んで,人口が大きいほど,次世代の最大技術水準の期待値が高くなることを数学的に示すこともできる。そのためには,同じ母集団から独立に抽出されたサイズNの標本があるとき,標本中の最大の値の期待値がNの増加関数になることを証明すればよい。直感的には,証明するまでもなくほとんど自明であるが,念のため論文末尾のAppendix 1で証明を与えておく。また,Appendix 1の証明からは,副産物として,標本中の最大の値の期待値がNとともに増加する速度は,Nの増大とともに逓減することが示される。すなわち,Nが小さいときよりも,大きいときのほうが,最大の技術水準の期待値に与える影響が小さいということである。このことは,Figure 2において,技術水準の時間変化を表すグラフの傾きは確かにNの増加とともに増加しているが,その傾きの増加分がNの増加とともに逓減していることを説明する。
一方,人口が技術の成長速度に与える定量的な影響については,残念ながら一般にはイノベーション率ϕだけから一意に決定することができない。ただし,ある種の標準化された速度ならば近似的に計算できる。世代tからt+1への最大技術水準の増加分をΔZmax,t,世代t+1における最大技術水準の理論分布の標準偏差をσmax,t+1で表すことにする。すると,Appendix 2で示すように,次の式が成立する。
 | (7) |
上の式で再びEは期待値を表し,左辺はある種の標準化された技術成長速度を表す。ここで二つ目の近似的等号は,0.45≈−0.78 log(0.562)なる関係式から導かれる。上式は,Nが大きくϕが小さいときに妥当な近似式である。大きなϕについても成立する,より正確な近似式はAppendix 2に与えてある。この式より,標準化された技術成長速度は世代あたりイノベーター数Nϕの対数とともに線形に増加することがわかる。そして,すでに論じたように,(log1=0より)Nϕ=0.562のときに速度の符号が入れ替わることも明らかである。この対数的な依存性は,Figure 3において10世代後の最大技術水準が人口に対して対数型の曲線を描いていることに対応している(ただし指数分布については片対数グラフであることに注意)。標準化された速度をデータから推定するのは容易ではないが,シミュレーションならば比較的簡単に計算できる。世代t+1を何度も繰り返し生成し,繰り返しごとの最大値の標準偏差を計算すれば,それがσmax,t+1のかなり正確な推定値を与えるので,左辺の計算に使うことができる。
これまでの議論で筆者が主張したいことの一つは,Henrichの想定したメカニズムを通して人口が技術の発展に与える影響を理解したり予測したりするために,各個人の技術水準が従う理論分布の形状の詳細や,分布がその形状をとる生物学的な背景に関する知識は必ずしも要求されないということである(Vaesen(2012)も参照)。これはモデルが,見かけよりも広い範囲の現実の事象に適用できることを示唆しており,定量的検証においてのみならずモデルの適用範囲に対する批判を検証するうえで役にたつ知見である。個人の技術水準に特定の分布を仮定することには,分布ごとに各々根拠があり得る。例えばアスリートのように人生の一定期間のうちに何度も同じ課題に挑戦し,そのうち最高の成績を技術水準とするならば,ガンベル分布などの極値分布が妥当かもしれない。一方で,技術レパートリーの大きさ(例えば,食用に適した野草を何種類知っているかというような民族学的植物学の知識量)を技術水準とし,各々の技術要素が教示者(あるいは自然環境)から等しい確率で伝達されるならば,レパートリーのサイズは二項分布やポアソン分布に従うだろうから,zを連続変数化するために中心極限定理を適用し,正規分布で近似するのがよいかもしれない。これまでの数学的議論には事例に適用するうえで幾つかの制約条件があるが,分布の制約としてはガンベルの吸引域にあることしか仮定していないので,上述のような背景の個別性を超えて広範な適用が可能である。
もちろん,個人の技術水準の分布を未知とした状態ではわからないこともある。そのような問題のうち,重要なものの一つは,イノベーション率ϕが一定の値に保たれるとすれば,それはどのようなメカニズムによってかということである。また,上で述べたように人口が技術成長の絶対速度に与える影響は,一般にはイノベーション率だけでは決まらない。これらの問題に答えるためには,学習に伴うエラーの理論分布に関する具体的な考察が必要である。実際の実証研究では,そのような理論分布は未知であることがほとんどだろうから,個人の技術水準の経験分布から理論分布を推定する必要があるだろう。そして,その理論分布には,事例によってさまざまなものがあり得る。しかしながら,手元にデータがないのであれば,考察を進めるにあたって特定の理論分布を採用する科学的な根拠は存在しない。そこで,尤もらしい分布を選ぶ代わりに,計算上便利な分布を採用するという戦略があり得る。実際にHenrichが個人の技術水準の分布として想定したガンベル分布は,Henrichモデルの挙動を解析的に予測するために最も都合の良い性質を持っている分布である。
以降の議論は,個人の技術水準がガンベル分布に従うという仮定のもと,世代あたりの技術水準の変化速度と人口Nの定量的関係を求めるためのものであり,Henrich(2004)の元々の仮定に沿うものである。以下では数式を用いた議論が多くなるが,次章「実証研究」との内容的な関わりはそれほど強くないので,以降は読み飛ばして次章に進んでもおおむね内容を理解できるだろう。
ガンベル分布の性質ここでは,ガンベル分布になじみのない方のために,いったん脇道にそれ,ガンベル分布の一般的な性質について説明をしておく。一般のガンベル分布は,最頻値aと尺度パラメータbの二つのパラメータを持つ連続変数の確率分布であり,生成される乱数の定義域は正規分布と同じく実数値全体である。ガンベル分布の確率密度関数は
 | (8) |
で与えられ,対応する累積分布関数は
 | (9) |
で与えられる。Figure 4(a)は密度関数(8)を図示したものであり,正規分布とは違って左よりも右の裾が厚いことがわかる。また,尺度パラメータbは,最頻値周りの分布の広がりの大きさを表し,bが大きいほど分散が大きくなる。乱数Xが式(8–9)のガンベル分布に従うとき,その期待値は
 | (10) |
で与えられる。ここで,γはオイラーの定数(もしくはオイラー・マスケローニ定数)と呼ばれる正の実数であり,その具体的な値はγ=0.5772156…である。式(10)より,ガンベル分布の期待値は,正規分布などとは異なり,最頻値よりもbγだけ右側にあることが明らかである(Figure 4(a)の垂直の破線)。このように,尺度パラメータbは,分散だけでなく期待値にも影響を与えることに注意すべきである。またガンベル分布の中央値は,関係式G(x)=1/2をxに関して解くことで容易に得られ,
 | (11) |
であることがわかる。式(10)と(11)より,中央値は最頻値より右にあるが,期待値よりは左にあることに注意されたい。よって,ガンベル分布から生成された乱数の半分以上は期待値より小さい値をとる。具体的には,ガンベル乱数が期待値より小さい値をとる確率は,G(E[X])=exp(−e−γ≈0.57程度である。言い換えると,期待値超過率は約0.43であり,その確率で乱数は期待値より大きい値をとる。
注)(a)最頻値a,尺度パラメータbのガンベル分布(垂直の破線は期待値),(b)個人の技術水準が従うガンベル分布の確率密度関数,(c)N=5人の最大技術水準が従うガンベル分布の確率密度関数(破線は個人の密度関数)。(b)(c)において濃い灰色の部分の面積は個人のイノベーション率,(c)において薄い灰色の部分は集団のイノベーション率を表す。
ちなみに分散は
 | (12) |
(πは円周率)で与えられることが知られており,こちらはbだけで決まり,最頻値aの影響は受けないことがわかる。さらに言えば,最頻値aは,分散だけでなく,分布の形状には一切影響を与えず,その位置だけを決定する。つまりaを動かしても,密度関数や累積分布は同じ形のまま左右にスライドするだけである。そのため最頻値aは,位置パラメータとも呼ばれる。なお,a=0, b=1のときのガンベル分布を標準ガンベル分布と呼ぶ。標準正規分布の期待値が0であるのに対して,標準ガンベル分布の期待値はγになることに注意しなくてはならない。
ガンベル分布は,極値分布と呼ばれる分布の一種であり,正規分布ほどではないものの,自然科学や社会科学のさまざまな場面で頻繁に登場する分布である。正規分布がよく登場することに理由があるのと同じく,ガンベル分布がよく登場することにも,やはり理由があり,それを理解することがガンベル乱数の性質を理解するうえで重要である。よく知られているように,正規分布には,中心極限定理が保証する特筆すべき性質,すなわち,どんな乱数の標本であろうと,乱数が同じ分布に従っており,独立で,標本サイズが十分に大きければ,標本平均は近似的に正規分布に従うという性質がある。ガンベル分布を含む極値分布にも似たような性質があり,およそあらゆる連続変量の乱数について,乱数が独立に同じ分布に従っており,標本サイズが十分に大きければ,その最大値は近似的にいずれかの極値分布に従うことが知られている。極値分布にはフレシェ分布,ガンベル分布,ワイブル分布の3タイプがあるが,指数分布や正規分布のような多くの馴染みのある分布に関して,標本の最大値がガンベル分布で近似できることがわかっている。このあたりの詳しいことに関しては,西郷・有本(2020)による日本語で読める参考書がある。また,さらに掘り下げた理論的詳細を学ぶことができる良書として,筆者がよく活用しているde Haan & Ferreira(2006)を挙げておく。
さて,正規乱数の標本の平均値(あるいは総和)は,近似的にではなく,厳密に正規分布に従うことを思い出してほしい。この性質は正規分布の再生性と呼ばれる。それと同じように,ガンベル乱数の標本の最大値は,近似的にではなく,厳密にガンベル分布に従う。この性質を,ガンベル分布の最大値安定性と呼ぶ(西郷・有本,2020)。この証明は非常に簡単である。全く同じガンベル分布に従うN個の独立な乱数があるとし,その標本の最大値が従う分布の累積分布関数Gmax(x)がどのように与えられるか考えよう。累積分布関数は,定義より,当の乱数がxより小さくなる確率に等しい。ここで発想の転換をして,標本の最大値がxより小さくなるということは,標本のすべての乱数がxより小さくなることと同じであることに注意する。一つの乱数がxより小さくなる確率はG(x)であるから,乱数の独立性より,すべての乱数がxより小さくなる確率はG(x)のN乗である。すなわち,最大値の累積分布関数は,
 | (13) |
で与えられることがわかる。ここで,三つ目の等式を導出するために,N=e logNなる式変形を用いた。最右辺の表現より,Gmax(x)は,最頻値a+b logN,尺度パラメータbのガンベル分布の累積分布関数であることが明らかである。すなわち,最頻値a,尺度パラメータbのガンベル分布に従う独立なN個の乱数の最大値は,元の分布を右にb logNだけスライドしたガンベル分布に従う。さて,Xmaxが当の標本の最大値を表す乱数であるとすると,上で明らかになった事実より,乱数Xmaxの確率密度関数と期待値が以下で与えられることがわかる。
 | (14) |
 | (15) |
このように,ガンベル分布は,「標本の最大値を選ぶ」という単純な操作から自然に導かれる分布であり,これが科学のさまざまな局面でガンベル分布が登場する理由である。
模倣の難度とイノベーション率それではHenrichモデルの解説に戻ろう。前々節までは,個人の技術水準が従う分布を明示しない一般的な議論を行ってきたが,ここからは,Henrich(2004)の仮定に従い,個人の技術水準がガンベル分布に従うと仮定した場合について議論を進める。Henrich(2004)に基づくこの特殊なモデルでは,αやβといった新たなパラメータが登場するが,本節では,これらの新たなパラメータが,これまで活用してきた個人イノベーション率ϕや集団イノベーション率ϕmaxとどのように関係しているのかを明らかにしよう。そのうえで,次節では,すでに一般論の下で導出した正の技術成長が起きる条件や,技術成長の速度が,新たなパラメータでどのように記述されるのかを確かめていくことにしよう。
まず,Henrich(2004)が仮定した個人の技術水準の分布を数学的に記述しよう。モデルの仮定を厳密に記述するため,現世代の中で最も大きなz値を持つ個体の技術水準をzmaxで表すことにする。次世代の個体は,全員がこの同じ個体を模倣対象とし社会学習を行う。Henrichは各次世代個体のz値が,最頻値zmax−α,スケールパラメータβのガンベル分布に従うと仮定した。すなわち,次世代個体のzの値は乱数であり,その確率密度関数は次式で与えられる。
 | (16) |
また,対応する累積分布関数は,
 | (17) |
で与えられる。また,Zが分布(16–17)に従う確率変数であるならば,その期待値は
 | (18) |
によって与えられる。また中央値は
 | (19) |
で与えられる。式(16–19)は,それぞれ式(8–11)のa, bにzmax−αとβを代入することにより得られる。Figure 4(b)は密度関数(16)を図示したものである。パラメータbとβの意味はほとんど同じであるが,aとαの意味はかなり違うので注意しなくてはならない。パラメータαは技術を模倣する際のある種の「難しさ」を表しており,αが大きいほど,模倣対象の技術水準であるzmaxに比べて,模倣者のz値の分布はより左に位置することになる。特に,αが−β log(log2)≈0.367βより大きければ中央値がzmaxを下回るため,半数以上の次世代個体は模倣対象よりも技術水準が低下すると期待される。そして,さらに技術模倣の難度αが増加して,閾値βγ≈0.577βを上回るとき,モデルは興味深いものになる。なぜならば,このとき,期待値(18)は模倣対象の技術水準zmaxよりも小さくなるので,もし集団に1個体しかいないならば,技術は衰退していくと期待されるからである。ここで,「では集団中に複数の個体がいれば,この技術の衰退を回避できるか」という問題が生まれる。この問題はすでに一般論の枠組みで取り扱ったが,次節において,より詳しい分析を行うことにする。
それでは,上で導入された個人の技術水準の分布が,個人のイノベーション率ϕや集団のイノベーション率ϕmaxとどのように関係しているのかを明らかにしよう。次世代の1個体の技術水準がzmaxを超えることは,模倣者が模倣対象を技術で上回ることを意味するので,その確率には特別な意味がある。すでに上で導入したが,改めてこの確率をイノベーション率と定義し,記号ϕで表すことにする。Figure 4(b)では,ハッチングした部分の面積がイノベーション率ϕを与える。式で表すと,イノベーション率は,
 | (20) |
で与えられる。ガンベル分布の期待値超過率は約0.43で与えられることを思い出してほしい。したがって,技術模倣の難度αが上昇して(分布は左にスライドする)βγに一致するとき,すなわち模倣者の期待値と模倣対象の水準が一致するとき,当然イノベーション率は0.43に一致する。これは,次のように式(20)にα=βγを代入することでも確かめられる。
 | (21) |
なお,集団イノベーション率は,式(20)を式(1)に代入することにより,次のように与えられることがわかる。
 | (22) |
N=1のとき式(22)は式(20)に帰着することに注意されたい。Figure 5に,尺度βで標準化された技術模倣の難度α/βに対して,いくつかのNの値を仮定し,集団イノベーション率ϕmaxをプロットした。模倣の難しさをαの代わりにイノベーション率で測ることにすると,個人イノベーション率が期待値超過率0.43を下回るほど模倣が難しい場合に,モデルは自明でなくなる(すなわち,1個体しかいない集団は技術を衰退させる)ということができる。最初に一般論として述べたように(そして次節で詳しく説明するように),たとえ個人イノベーション率が0.43より小さくても,集団イノベーション率が0.43を上回っていれば,集団の最大の技術水準は1世代で増加することが期待される。Figure 5より,個人イノベーション率が小さいとき(グラフの右側)でも人口Nが十分に大きければ,0.43を超える集団イノベーション率を確保できることがわかる。

注)集団サイズはN=1, 10, 100, 1,000, 10,000の5通り。N=1のとき(太い実線),集団のイノベーション率ϕmaxは個人のイノベーション率ϕに等しい。水平の破線はガンベル分布の期待値超過率0.43を表しており,垂直の縦線は,個人のイノベーション率が期待値超過率に一致する(ϕ=0.43となる)模倣難度を示している。垂直の破線より右側では,個人の期待値がzmaxよりも小さいので,正の技術成長を引き起こすために集団の力を借りる必要がある。
このように,模倣の難度をαの代わりにイノベーション率で測ることが可能である。パラメータαはガンベル分布に対して定義されているが,ϕはどんな分布でも一意に定義されるので,特定の分布に依存しない議論をするときはϕを使うほうが便利である。しかし,ϕはβにも依存するので,二つの指標は等価ではないことに一応注意すべきである。式(20)からわかるように,イノベーション率は尺度パラメータβによって標準化された模倣難度であるα/βと一対一に対応している。技術水準zの測定単位に重要な意味があるならば,αやβのパラメータを独立に考えることにも意味があるが,そうでないならば,標準化された模倣難度α/βを用いて議論するほうが自然であると言える。これらのことから,α/βと一対一に対応するイノベーション率を模倣難度の指標として用いることが正当化されるだろう。
最大技術水準の成長速度ここでは人口サイズが技術成長速度に与える定量的な影響に関する分析を行う。次世代の各個体の技術水準はガンベル分布(16–17)に従うので,次世代のうち最大の技術水準を持つ個体の技術水準は,ガンベル分布の最大値安定性に関する既出の議論より,右にβ logNだけ右にスライドしたガンベル分布に従うはずである。したがって,その確率密度関数,累積分布関数,期待値はそれぞれ
 | (23) |
 | (24) |
 | (25) |
で与えられる。ただしZ′maxは次世代における最大の技術水準を表す確率変数である。式(25)より,一世代あたりの最大技術水準の変化量ΔZmaxの期待値は,
 | (26) |
となり,予想されたように人口Nの増加関数であることがわかる。なお,技術水準が長期的に増加していくには,E[ΔZmax]が正でなくてはならず,その条件は,式(26)の最右辺を用いると,
 | (27) |
である。条件式(27)は,Henrich(2004)の式(3)およびKobayashi & Aoki(2012)の式(8b)と全く同じものである。我々はすでに式(27)を一般化した式(2)を,個人の技術水準の分布に関する情報を用いることなく導いていたことを思い出してほしい。個人のイノベーション率に関する式(20)を用いて,式(27)のα/βを消去すると,
 | (28) |
が得られ,これは計算誤差を除いて式(2)と同じ条件式である。つまり,我々は,個人の技術水準がガンベル分布に従うという特殊な場合について,一般的な条件式(2)が正しいことを別ルートで確認したことになる。個人の技術水準がガンベル以外の分布に従う場合でも,同じルートで条件式(2)が成立することを確認することが理論的には可能であるが,その場合は,最大値安定性が利用できないので,極値理論を使った込み入った議論が必要になる。ここではそういった議論は本質的ではないので控えることにする。
上述の数理モデルの仕組みについての解説からわかるように,Henrichモデルにおいて技術が長期的に改善していくためには,世代あたりに一定数を超えるイノベーターが必要である。その閾値は,個人の分布がガンベルの吸引域にあり,イノベーション率が一定かつ小さいならば,技術水準の測定方法や伝達様式の詳細には依存せず,世代あたり約0.56人である。これらの結果はすべて離散世代モデルから導かれたものなので,野外で得られたデータへの適用は注意が必要だが,実験では離散世代の設定はむしろ自然である。Henrichモデルを定量的に検証する一つの方策は,モデルから予測される上記の閾値をデータから推定される閾値と比較することである。
約0.56人/世代という数字は個人のイノベーションがまれな場合のみ使える近似だが,その仮定が当てはまらない場合は,閾値の予測において多少慎重になる必要がある。実験室実験の場合は,あまりに個人のイノベーション率が小さいと,現実的なサンプルサイズでイノベーションを引き起こすことが難しくなる。よって正の技術成長を引き起こしたいならば,個人あたりのイノベーション率が大きくなるように,容易な課題にせざるを得ない。その場合は,かなり小さい人数で正の技術成長が起きてしまうので(というより,そのように課題を設定したので),Nが大きいこと(すなわち極値理論)を利用したガンベル近似が使えず,0.56人/世代という閾値が妥当でなくなる。ただし,その場合でも,個人の技術水準の分布がガンベル分布に従う場合は例外的に,条件式(2)は厳密に正しい。ただイノベーション率ϕは小さくないので,ϕの微小性を利用した近似条件式(4–6)の適用には注意が必要である。例えば,イノベーター数の閾値を正確に計算する際は,条件式に次のような補正が必要である。
 | (29) |
上式は,式(2)の両辺にϕを掛けることで得られる。また,上式はϕが0に近づくに従って条件式(6)に近づく。この式の右辺にある補正係数(丸かっこ内の分数)はϕの減少関数になっているので,正の技術成長に必要なイノベーター数の下限値は,ϕが大きい場合は0.562人/世代よりも小さくなる。例えば,ϕ=0.1のとき,イノベーター数の閾値はおよそ0.533人/世代にまで減少する。この補正係数は,ϕが1に近づくとき,0に近づいていくが,実際にはそのような大きな補正が必要な場面は存在しない。なぜならば,個人の技術水準がガンベル分布に従い,なおかつイノベーション率ϕが分布の期待値超過率0.43を上回るような場合は,一人だけで正の技術成長を引き起こせてしまう。よって,集団サイズを減らしても負の技術成長を引き起こすことは不可能である。したがって,閾値を用いた検証において補正係数の下限は−{0.43/log(1−0.43)}≈0.765であると考えてよい。このとき,イノベーター数の閾値は式(29)より,0.562×0.765≈0.43であるから,イノベーター数の閾値は0.43と0.562の間にあるとしてよい。
多くの実験では個人の技術水準がガンベル分布に従わないだろう。その場合は,補正条件式(29)ですらそのまま使えない。しかしながら,ガンベルからの乖離が大きくないならば,実際の閾値は式(29)が定める閾値と似た値になるものと推測される。個人の技術水準が例えば正規分布のようなガンベル以外の特定の分布に従うとき,正確な閾値を計算するには,ガンベル近似で予測された閾値(29)の近傍で,シミュレーションを行い,実際に技術成長速度の符号が反転する点を見つけるのがよい。別の方策として,以下のように,自身の実験系でこの手の誤差がどの程度大きくなりえるのかを解析的に予測しておくことも,また有用である。閾値の予測はすべて最大技術水準の期待値超過率に基づく議論に立脚するので,極値分布近似がもたらす閾値の誤差もまた,最大技術水準の期待値超過率を実際よりも過大・過小評価することによってのみ生じることに注意されたい。極値理論より,次世代の各個人の技術水準がガンベルの吸引域にある分布から抽出されるとき,集団サイズが増加するに従って,次世代の最大値の分布の期待値超過率はガンベル分布の値0.43に近づいていくはずであるが,小さい集団サイズでは,実際の期待値超過率は0.43から乖離する。実際の期待値超過率とその極限値0.43の差分は集団サイズNに依存しているだろうから,それをϵ(N)と書くことにする。ここで,各個人の技術水準の分布の期待値超過率は0.43+ϵ(1)と書けることに注意してほしい。したがって,個人の技術水準の分布が正規分布やロジスティック分布のような左右対称の分布であればϵ(1)≈0.5−0.43=0.07である。また,個人の技術水準の分布がガンベルのときは,最大値安定性よりNによらずϵ(N)=0である。この記法を用いると,技術成長の速度が正の値をとるとき,「数理モデル」の章において用いたのと全く同じ論理に従い,不等式(1−ϕ)N<0.57−ϵ(N)が成立していなくてはならないことがわかる。この不等式を変形することにより,次の条件式を得る。
 | (30) |
この不等式は,左右両辺にNがあるため,Nの閾値を与える条件式としては理解しづらい。ただし,多くの場合ϵ(N)の絶対値はNの増加とともにおおむね単調に減少し0に収束していくことが予想されるので,|ϵ(N))|<|ϵ(1)|を仮定してよさそうである。そこで,極値分布近似がもたらす閾値の誤差の(予測値に対する)百分率を,次の式によって保守的に評価できるだろう。
 | (31) |
この式より,例えば個人の技術の分布が左右対称な分布であれば(ϵ(1)≈0.07),極値分布近似により最大で約23%の過小評価が生じることがわかる。言い換えれば,実際の閾値は,近似的予測値の最大123%であり得る。よって,実験では,0.562人/世代よりもう少し多めにイノベーターを用意しないと,正の技術成長が起きない。逆に,例えば個人の技術水準が(ガンベルより非対称性の強い)指数分布に従う場合,期待値超過率は0.368なので,ϵ(1)≈0.368−0.43=−0.062である。したがって,式(31)より,極値分布近似により最大で約18%の過大評価が起きる(実際の閾値は最小で予測値の82%)。これらはあくまで誤差の保守的な推定値なので,実際の誤差はもっと小さいだろう。また,一般に,個人の分布とガンベルの期待値超過率で測った差異,すなわちϵ(1)の絶対値が大きいほど,極値理論による近似の誤差が大きくなると期待されることは覚えておいたほうがよさそうである。極値分布近似による誤差を可能な限り小さくするために,測定方法を工夫して個人の水準の分布をガンベルに近づけておく(すなわちϵ(1)を小さくしておく)という戦略があり得るが,それについては後の節で論じることにする。なお,かなり数学的な話題になってしまうが,ガンベルの吸引域にある任意の分布に対して極値分布近似の誤差を抑え込むことができる,式(31)の自明でない上限と下限が存在することが予想される。この問題に対しては,筆者の勉強不足により即座には答えを見出すことができないため,将来の課題として残しておくことにする。
実験では,多くの場合サンプルサイズの制約が厳しいであろうから,与えられた範囲のグループサイズで技術成長速度の符号が切り替わるために,課題の難易度を適切に設定する必要がある。その目的には,式(5)を使うこともできるが,当該の式はイノベーション率ϕの微小性を用いた近似式なので,その正確さを評価しておくべきである。イノベーション率が大きいときの対応する条件式は,式(2)を次のように変形することによって得られる。
 | (32) |
Figure 6は,条件式(32)とその近似(5)によって定められるϕの閾値をNの関数としてプロットしたものである。Figure 6より,課題の難易度を設定するという目的においては,極端に小さいグループサイズNを設定しない限り,近似式(5)でほとんど事足りることがわかる。したがって,例えば予算や被験者プールサイズの制約でグループサイズを予定の半分にしなくてはならない事態が生じたならば,課題の難易度を下げてイノベーション率を倍にしなくてはならないと結論してよいだろう。また冗長になるので詳しい議論は省略するが,やはりこの場合でも,極値分布近似が及ぼす影響を適切に評価しておくべきことは言うまでもない。

注)実線は,個人の技術水準がガンベル分布に従う場合の厳密な条件式(32)に基づく。点線は,ϕが小さいときの近似式(5)に基づく。
前節では,技術成長の速度の符号が切り替わるパラメータ閾値を用いて定量的な検証を行う方法について論じた。これに対して,実験室内で正の技術成長を起こすことは最初から放棄して,技術の衰退速度をグループサイズの異なる条件間で比較したり,理論的な予測値と実測値を比較したりするといった方法がある。Muthukrishna et al.(2014)が人口仮説の検証のために実施した二つの実験のうち,二つ目(実験2)はこの方法を採用している。この実験は,ロッククライミングで用いる専門的なロープの結び目を作る技術を世代間で伝達させるものである。初期世代は実験者によるインストラクションを経て十分にトレーニングされるが,後続の世代は,前の世代が一人称視点で録画した作業工程のビデオを見本に課題に取り組む。彼らは,グループサイズがN=1の条件とN=5の条件を比べて,人口仮説の予測通り後者のほうが世代の経過に伴う結び目の技術の衰退を小さく抑えられることを示した。
こういった手法は,負の成長速度を条件間で比較するものである。個人の技術水準が,成果物と手本の「近さ」によって測られるため,十分にトレーニングされた初期世代を超えて技術が正の成長を遂げることはない。また,たとえ技術水準を目標物との「近さ」ではなく成果物の機能で測ったとしても,現実の完成された技術を用いている以上,常識的なサンプルサイズと1セッション数十分の学習時間で,世代あたり0.56人のイノベーターを生み出すことはあり得ない。おそらくMesoudi(2011)のモデルにおいて想定されたように,成熟した技術ではイノベーションが困難になるので(zmaxの上昇とともにϕが低下する),実験室内で正の文化進化を漸進的に引き起こすには,初期状態を野外よりも水準のかなり低い未熟な状態に設定するか,誰も取り組んだことがないような人工的な課題を設定するしかない。理想的には,文化進化は実験室内だけで「閉じて」いてほしいので,前者の方法をとる場合は,被験者が課題の熟練者ではないということを事前に保証しておくべきである。
文化進化が実験室で閉じないことの問題点は,本稿の主題と深い関連がある。例えば,人口仮説の検証として実際に行われた,紙飛行機を用いた実験を考えてみよう(Caldwell & Millen, 2008a, 2008b, 2010; Fay et al., 2019)。この実験では,被験者はA4用紙を用いて紙飛行機を製作する課題に取り組み,その飛距離(正確には3回の飛行テストのうち最大の飛距離)が個人の技術水準に相当する。A4用紙で作成できる紙飛行機の技術文化は,野外ですでに成熟しており,この点ではMuthukrishna et al.(2014)の結び目と似ている。しかしながら,結び目の実験と異なるのは,多くの被験者が幼少期にかなりのトレーニングを受けている可能性がある点である。言い換えれば,実験のセッションという短い期間での模倣学習が技術水準の分布に与える影響は,相対的に小さいことが予測される。だが,この推測にもかかわらずCaldwell & Millen(2008a)の実験では第1世代から第10世代までの間で飛距離の平均値が2 m前後から7 m前後まで漸進的に増加している。だが,Caldwell & Millen(2010)およびFay et al.(2019)による同じ課題を使った後続の実験では,世代の影響はもっと小さく見える。ちなみに,筆者が試みに手本なしで同じ課題に取り組んでみたが,得られた記録は軽く10 mを超えたので,むしろ初期世代の平均値が2 m程度ということの理由が重要かもしれない。なお,Caldwell & Millen(2010)およびFay et al.(2019)は,ともに紙飛行機実験で集団サイズの影響についてネガティブな結果を報告している。Muthukrishna et al.(2014)はそれに対して,紙飛行機の模倣は結び目などと比較すると容易すぎるからだろうと推測しているが,Kempe & Mesoudi(2014)は,紙飛行機の適応度地形は多峰的で複雑なので,複数人の情報を組み合わせることが難しいからだろうという別の推論を行っている。Fay et al.(2019)自身による解釈は,このどちらとも異なる(後述)。
紙飛行機課題の妥当性はさておき,一般的に言うと,実験系が閉じておらず,しかも被験者が熟練者であるような課題を用いることは,Henrichモデルの検証には不向きであると思われる。例えば,何らかの楽器で,プロの演奏家を集めてきて演奏技術を伝達させる実験を行ったとしても,前世代のzmaxに次の世代の演奏技術が左右されることはほとんどないだろう。したがって,前世代を超える確率,すなわちイノベーション率が一定であることはあり得ない。これは極端な例だが,例えば「肉じゃが」を作る技術など,現実集団で広範に流布している技術を課題に使うことには多かれ少なかれ同様の問題が絡むはずである。Henrichモデルの検証としてだけでなく,野外の熟練者を用いる「開いた」実験は人口仮説の検証手法としても問題がある。なぜなら,それが未熟な段階にある技術の進化や,タスマニアのように成熟した文化が大陸から断絶した直後の様子をシミュレートできないからである。熟練者を用いている以上,前者に当てはまらないのは自明であるし,後者についても,タスマニアの技術文化はタスマニアだけで閉じていたはずである。
未熟期における技術の累積的文化進化を再現した実験としては,Muthukrishna et al.(2014)の第一の実験(ドローイングツールによる作図課題)がある。この実験では,(Linuxユーザーには馴染みの)ドローイングツールGIMPを用いて,ある複雑で幾何学的な図形のイラストを複製する技術を世代間で伝達させている。個人の技術水準は,成果物である画像の完成度をある方法で定量的に評価したものである。未熟者を被験者として使っているところは結び目の実験と同じだが,結び目の実験とは違って,初期世代はトレーニングされず,正の技術成長が生じることを期待した設定になっている。この実験で,彼らはやはりグループサイズ1の場合と5の場合を比較しており,後者においてのみ,世代とともに被験者の成果物の完成度が高まることを確認している。
最後に,上で論じた実験系の「閉鎖度」に関連して,Derex et al.(2013)の実験に触れておきたい。この実験は,やはりHenrichモデルのメカニズムを念頭に人口仮説を検証したものであるが,オリジナルのコンピューターゲームを用いている点で,より閉じていると言える。残念ながら,上で触れた実験研究(Caldwell & Millen, 2010; Fay et al., 2019; Kempe & Mesoudi, 2014; Muthukrishna et al., 2014)とは異なり,複数の点でHenrichモデルとはかなり異質で複雑な設計を採用しているので,本稿で得られた知見に基づく解釈が難しい(それどころか,0,1ベクトルモデルを含む既存のどのような数理モデルとも整合性がない)。第一に,性質の異なる二種類の仮想技術(矢尻と漁網)が単一の実験内で同時に用いられており,各試行において被験者は,矢尻課題に取り組むか,漁網課題に取り組むかを選択しなければならない(二重課題)。矢尻はその機能(収穫量)が最終的な形状のみに依存しているが,漁網は形状だけでなく制作過程(操作の順序)にも依存している。したがって矢尻のほうが集団中で容易に記憶され維持されるが,その代わり漁網のほうが潜在的に高い収穫量を生み出せるようになっている。そのため,Henrichモデルの枠組みに当てはめるために技術水準を1次元変数に要約してしまうと,背後にある複雑な適応度地形が隠蔽されてしまう。第二に,世代更新は行われず,各試行において,被験者には,同じグループの成員が前試行で作成した矢尻と漁網の収穫量だけが成績順に表示される。そして,被験者はその中から一つだけを選択し,実際の制作工程を観察することができるようになっている。試行数は全部で15である。第三に,被験者には毎試行「生活費」が課され,ゲーム中に貯金が足りなくなると,「死んで」しまい(つまりゲームオーバーになる),それ以降のすべての試行の機会を失う。Derex et al.(2013)の実験で注目に値することの一つは,初期状態の技術が最善でも最悪でもないということである。彼らの報告は人口仮説の主張と整合性があり,大きいグループ(N=8, 16)においては矢尻の成績が初期よりも改善し,漁網の成績は維持されたが,小さいグループ(N=2, 4)では矢尻の成績が改善せず,漁網の成績は低下してしまった。また,矢尻と漁網の双方について,大きいグループのほうが小さいグループよりも高い確率で集団中に維持された。こうしたオリジナルのコンピューターゲームを用いれば,実験の閉鎖度は高くなるが,一方で課題の適応度地形が自然界の法則とほとんど無関係になってしまうので,実験室外部に実験結果を外挿する際の妥当性は低下する。こうしたジレンマに対処するためには,おそらく同一の構造を持った伝達連鎖実験において,人工的な課題と自然な課題の両方を相補的に用いるのがよい。
上で言及した既存研究はすべて定量的な技術成長速度の条件間比較を行っているが,Henrichモデルの仮定や予測との無矛盾性を確認しているだけなので,その意味で定性的検証である。技術成長速度を用いたHenrichモデルの定量的検証は,閾値を用いた定量的検証よりも難しい。今のところ,そのような検証に利用可能な解析的結果としては,式(7)が得られているが,この式の左辺で定義されている標準化された速度をデータから推定するのは,一般に困難である。残念ながら,極値分布近似が妥当なパラメータ領域においてすら,標準化尺度σmax,t+1は一般にNや個人の技術水準の分布の詳細に依存してしまう。したがって,異なる条件間で技術成長速度の比率をとったとしても,標準化尺度の影響を消し去ることはできない。ただし例外として個人の技術水準がガンベル分布に従う場合は,標準化尺度がNに依存せず,技術成長速度と人口の対数logNの関係が線形になるので,Figure 3と同じものを実験結果を用いて作図し,予測とデータを比較することができる。
理論的には,個人の技術水準が従う分布がガンベル以外の場合でも,十分な量のデータがあれば標準化尺度の推定は可能である。しかしながら,そこまで大量のデータが得られるのであれば,個人の技術水準の分布を推定し,それを用いて技術進化をシミュレーションし,シミュレーションの結果と実験の結果を比較するほうが素直である。だが,データ量の観点から,こうした方法はあまり実際的ではないように思われる。おそらく,測定方法を工夫して個人の技術水準の分布をガンベルに近づけておくか,あるいは速度を使った検証については,おおむねグループサイズに対してFigure 3のような対数型の関係が成立することを確認するといった,おおざっぱな検証で妥協するのが,現段階では実際的かもしれない。
技術水準の測定方法Henrichモデルにおいては,個人の技術水準zをどのように測定するかということに関して制約がないので,基本的には実験者にとって都合の良いように,好きな測り方をすればよい。ただし,いくつか注意事項がある。まず,大前提として,分析の対象となる「技術水準」,すなわちz値は,あくまで個人の属性でなくてはならない。もちろん,技術水準の集団平均や集団中の最大技術水準といった量が関心の的になってはいるが,それらは中央値や最頻値といったものと同じく,技術水準の分布を評価するための要約統計量に過ぎない。したがって,関心の的となる「技術水準」が,個人の技術水準の要約統計量ではない場合,問題が生じる。例えば,「技術水準」を,「集団中に存在する道具の種類の数」として定義する場合である。ほとんどの民族学データセットには,集団の成員である個々人の道具レパートリーに関する情報は含まれておらず,個々の道具について存在が確認されたかどうかの情報だけが記録されている。したがって,技術水準の定義としては,どうしても上述のような集団レベルでの定義を採用せざるを得ない。このように定義された「技術水準」は対応する個人の属性,すなわち各成員の道具数の要約統計量になっていない。言い換えると,全成員の技術水準がわかっていても,その情報だけから,上で定義された集団の「技術水準」を計算することができない。各成員が少数の道具しか持たないからといって,集団中に存在する道具の数が少ないとは限らないからである。そのように定義された集団の「技術水準」を各成員の技術水準から計算するためには,各成員が持っている道具の集合が,成員間でどのように重複しているかという,低水準の情報がなくてはならない。このように,Henrich的ではない方法で「技術水準」を定義すると,たとえ人口と「技術水準」の間に何らかの相関を見出したとしても,それはHenrichモデルの検証にはなっていない。
結論として,民族学的データセットを用いて人口仮説の検証を行った実質すべての既存研究は,その結果のポジティブ(Collard, Ruttle et al., 2013; Kline & Boyd, 2010)・ネガティブ(Collard, Buchanan et al., 2013; Collard et al., 2005, 2011; Read, 2006)にかかわらず,少なくともHenrichモデルの検証としては問題を抱えているのであって,このことはAoki(2018)によっても的確に指摘されている通りである。あくまで集団中に存在する道具の種類に関心があるならば,Henrichモデルのような高水準情報のモデルではなく,0,1ベクトルモデルのような,個人の文化要素レパートリーを明示的に記述するモデルを使うほうがよい(Aoki, 2018)。この問題に関連して,Kempe & Mesoudi(2014)のジグソーパズルを用いた人口仮説の検証実験は興味深い。彼らの課題では,個人の技術水準は個人が正しく組み合わせたピースの数であるが,一方で,集団の技術水準は,「集団の成員の少なくとも誰か一人が正しく組み合わせることができたピースの数」と定義されている。上述と全く同じ理由で,集団の技術水準は,個人の技術水準の要約統計量になっていない。Kempe & Mesoudi(2014)は,グループサイズが1と5の場合で比較し,やはり後者の場合においてのみ,個人の技術水準も集団の技術水準も世代とともに増加していくことを確認している。ちなみにKempe & Mesoudi(2014)の目的はHenrichモデルの検証ではなく,人口仮説の論拠となる他のメカニズムを提示することである(後述)。
第二の注意事項は,より技術的である。Henrichモデルの各種の計算は,少なくとも個人の技術水準の分布が連続変量であり,滑らかな理論分布を持っていると仮定している。また,正の技術成長を生むためのイノベーター数の閾値0.56人/世代という数字は,個人の分布がガンベルの吸引域にあるという仮定に基づいている。個人の技術水準の分布が,異なる極値分布,すなわちフレシェ分布やワイブル分布の吸引域に属する場合は,注意が必要である。フレシェ分布は,密度関数の右裾の減衰がガンベルよりも遅い分布であり,各個人が無視できない確率でずば抜けたイノベーションを起こすような場合には最大の技術水準がフレシェ分布に従う可能性があるが,実験でそのような設定を採用する理由はないし,また実際的でもない。逆に,一様分布のように,個人の技術水準の分布に明確な上限がある場合は,最大の水準は人数Nが大きいとき近似的にワイブル分布(上限のある極値分布)に従うが,こちらのほうが実験との関連性が強い。個人の分布がワイブルの吸引域にある場合のHenrichモデルの振る舞いは全く研究されておらず,今後の課題であるが,少なくとも期待値超過率の値がガンベル分布の0.43とは違った値になる。これ以上ワイブル分布について本稿で深く議論をすることはあまり生産的ではないと思われるので慎みたいが,現時点では,実験を計画する際に,個人の技術水準の分布がガンベルの吸引域に入るように調整しておくのが,結果を解釈するうえで無難であろう。
とはいえ,車輪をA地点からB地点まで転がすときの所要時間(Derex et al., 2019),組み立てることができたジグソーパズルのピース数(Kempe & Mesoudi, 2014),ターゲット画像との類似度(Muthukrishna et al., 2014)などといった,明らかな上限値の存在する数値が技術水準の指標である場合に,何らかの尺度の変換により,技術水準の分布がガンベルの吸引域に入るようにできるのかという問題は,筆者の不勉強と考察不足のために,ここでは答えることができない。一方,紙飛行機をできるだけ遠くに飛ばすとか,自作の籠でできるだけたくさんの米粒を運ぶ(Zwirner & Thornton, 2015)とか,パスタと粘土を使ってできるだけ高いタワーを作る(Caldwell & Millen, 2008a, 2008b)とかいった,明確な上限値はないものの,かといって無限に大きな技術水準はありえないだろうといった課題の場合に,技術水準の分布がガンベルの吸引域に入ると仮定してよいのかについても,今後の研究が必要である。
個人の技術水準の分布がガンベルの吸引域にある場合でも,実験においてガンベル近似が成り立つグループサイズを確保するのは多くの場合実際的ではない。それでも本稿で展開してきた解析的予測を定量的検証に有意義に活用したい場合は,そもそも個人の技術水準がガンベル分布に従うように測定を行うのが一つの方法である。例えば,各被験者に,同じ課題に何度も繰り返し取り組んでもらい,得られた得点の中で最も高い得点を記録するという手続きをとれば,単一の得点の分布がガンベル吸引域にある限り,記録される得点の分布はガンベル分布に近づくだろう。しかしながら,この方法には,思いつく限りでも二つの課題がある。一つ目は個人差を取り除けないので,個人を固定すればガンベル分布に従っても,集団全体はガンベルではなく,ガンベルと個人差の分布の混合分布からのサンプルになる可能性があることである。二つ目は,繰り返し試行の際に生じる個人学習の影響である。個人学習があると,個々の測定値の理論分布は試行回数の増加とともに変化していく。この経時的な変化が少ないほうが,繰り返し試行の最大値が従う分布はガンベルに近くなるが,一方で個人学習が少なすぎると,複数世代を経たときの技術の成長速度も遅くなってしまい,技術成長速度の条件間差異を検出するのが難しくなってしまう可能性がある。これらの問題がどこまで深刻なのかは,広範なシミュレーションや実験によって評価すべきであるが,それについては将来の研究に委ねることにしたい。
伝達様式数理モデルの仕組みの解説からわかるように,伝達様式がHenrichモデルにとって重要なのは,それが個人の技術水準の理論分布とzmaxの関係に影響を与え得るからである。Henrichモデルで仮定されているように,個人の技術水準の分布がzmaxに「引っ張られて」移動し,イノベーション率が一定に維持されるならば,伝達様式が何であれ本質的な結果は変わらない。極端に言えば,その条件が満たされるならば,技術は伝達される必要すらなく,文化でなくてもよい。したがって,実際の集団では「Best-of-N」の伝達は困難であるという,よくある伝達様式の仮定に関する批判(例えばBentley & O’Brien, 2011)は,重要であるに違いないが,限界まで本質に迫ってはいない。Henrichモデルを成立させる他の伝達様式や伝達すら必要としない生物的背景が存在するかもしれないからである。
個人のイノベーション率ϕは,実験設定と伝達様式の組み合わせによっては人口Nに依存することがあるので注意しなくてはならない。この問題を理解するには,社会的連結度と人口を混同しないことが大切である(Kobayashi et al., 2016)。ここで社会的連結度とは,次世代の個人が観察できる現世代の人数Kである。Henrichの元々の想定ではKは常に人口Nに等しく,人口Nを増やすと連動して連結度も増加するようになっており,このことによってイノベーション率ϕのN独立性が実現されている。ここで問題にしたいのは,連結度Kがイノベーション率ϕに与える影響である。例えばすでに言及したKempe & Mesoudi(2014)のジグソーパズルを用いた実験では,次世代の各成員は,同じグループの現世代のN人の成員(N=1もしくは3)が各々組み立てたN個の未完成のパズルを参考にして自らのパズルを組み立てる。このとき,当然ながらN人が組み立てたパーツには重複しない部分があるので,一人だけの未完パズルを見る場合よりも,観察者は多くの情報を得ることができる。Kempe & Mesoudi(2014)はこれを4世代繰り返し,グループ条件(N=3)では技術水準(組み合わせることができたピースの数)が世代とともに増加したが,個人条件(N=1)ではそのような正の技術成長がみられなかったことを報告している。彼らのメカニズムにおいて,グループサイズを増やしたときに学習者にとっての情報が増えるのは,連結度Kを増やすことによってイノベーション率ϕが増加することに対応しているのであって,人口Nが直接ϕに正の影響を与えているわけではないことに注意すべきである。彼ら自身が述べているように,このメカニズムは,ϕが一定のまま作用するHenrichモデルのメカニズムとは異なるものである。残念ながら,Kempe & Mesoudi(2014)はNとKを独立に操作した実験を行っていないので(これは容易に実装できる),得られた効果に対してHenrichのメカニズムと彼らの提唱するメカニズムが各々どれだけの量的な貢献をしたのかがわからない。なお,Muthukrishna et al.(2014)のGIMPの実験においても,被験者が複数人からの情報を合算して利用していることを示唆する分析結果が得られている。
Kobayashi & Aoki(2012)は理論研究だが,次世代の各成員が,現世代のN人のうちランダムに選ばれたK人だけを観察でき,K人中の最大の技術水準を持つ成員から学習を行うとした拡張(いわゆるbest-of-K学習)を行い,連結度Kと人口Nの影響を分離して分析している。このKは,上で論じたMuthukrishna et al.(2014)(あるいはCaldwell & Millen(2010))のKと少し意味合いが違うことに注意すべきだろう。Muthukrishna et al.(2014)では観察者はK人全員の技術の内容を観察するが,Kobayashi & Aoki(2012)ではK人のうちベストなものの内容だけが観察される。Kobayashi & Aoki(2012)のシミュレーションによれば,Kの増加はNの増加と定性的に同じ効果をもち,状況によってはNよりも定量的に大きな影響をもたらすことが確認されている。また,Baldini(2015)も類似のシミュレーションを行っており,同様の報告をしているほか,Kobayashi et al.(2016)は文化遺伝子共進化モデルの枠組みの中でNとKの影響を分離した分析を行っている。彼らのモデルで社会的連結度Kを固定にしたままNを増加させると,確かに優れた個体が出現する確率は高まるものの,その個体が次世代の各々にロールモデルとして発見される確率は低下してしまう。比喩的に表現すれば,これは次世代の個々人にとって,「踏み台」の高さが変わらないまま越えなければならない「ハードル」が高くなってしまうことを意味する。よって個人のイノベーション率ϕが低下し,Nの増加がイノベーター数Nϕに与える効果は比例的ではなく減速的になってしまう。一方Nを固定したままKを増加させると,ハードルが一定のまま踏み台が高くなる(すなわちϕが増加する)ことにより,イノベーター数Nϕが増加する。この類推より,イノベーション率ϕが一定のまま人口を増加させるという操作は,踏み台とハードルの双方の高さを同じだけ増加させることを意味することがわかる。そしてHenrichモデルでは,これがN=Kという隠れた前提により実現されている。
一方,Fay et al.(2019)によれば,連結度Kの増加が逆にイノベーション率ϕを低下させることもあり得る。その場合,Nを増加させることで生じるHenrich的な正の効果と,Kを増加させることによるϕの低下という負の効果が相殺して,イノベーター数Nϕに対する人口の影響が消えてしまうことが起き得る。すでに述べたように,Fay et al.(2019)は紙飛行機課題を用いた実験研究であり,集団サイズNの影響に関するネガティブ・リザルトを報告したものである。彼らによれば,観察できる模倣対象(すなわちK)が増えると,過剰な情報で学習者の作業記憶が飽和し,それによって伝達の忠実さが低下してしまうことで,技術成長が阻害される。彼らの実験では,N=K=1のときにのみ正の技術成長が起きており,N=K=2やN=K=4では全く技術成長が起きなかったので,もし彼らの解釈が正しいとすれば,むしろ作業記憶に対する負の効果がHenrich的な正の効果に勝っていると考えられる。ここでもやはり,NとKを個別に操作した実験がなされていないことが残念である。なおFay et al.(2019)は彼らの成果を一般の場合に外挿し,人口仮説がまともに機能する場面は現実ではまれであるという強い主張をしたが,Martens(2019)は,名声バイアスなどのバイアスを利用することで学習者は優れた個体だけを選択的に観察できるので,作業記憶が不足してしまうことは起きないと反論している。
なお,技術の適応度地形が複雑な場合は,連結度が高すぎると集団全体が局所的な最適解にトラップされてしまうことがあり,そのような場合は中程度の連結度により正の技術成長が最も促進される(Derex & Boyd, 2016; Derex et al., 2018)。適応度地形の多峰性と連結度の関係は大変興味深いトピックだが,本稿の主題から外れるので,これについての考察は慎んでおく。
本稿では,一般の読者に向けてHenrichモデルの詳細な解説を行うとともに,今まで余り注目されてこなかったイノベーション率の概念について踏み込んだ考察を展開した。そして,そこで得られた知見に基づき,人口仮説やHenrichモデルの検証として実施された既存の研究を評価するだけでなく,今後実験により検証を行ううえで注意すべき事項について雑多な議論を行った。読者が少しでもHenrichモデルのメカニズムと適用範囲について理解を深め,その検証や精緻化あるいは応用に関心を持っていただけたなら,本稿の目的は達成されたと言える。
「数理モデル」の章で展開された理論的考察には,既存研究の内容だけでなく,本稿独自のアプローチや一般化も含まれているため,章のどの部分がそれらに対応しているのか,ここで大まかに整理しておこう。当該の章のうち,「仮定」,「ガンベル分布の性質」,「模倣の難度とイノベーション率」,「最大技術水準の成長速度」と題した四つの節で解説した内容の大部分は,Henrich(2004)がその本文部分で得た結果のうち筆者が核心であると考える部分を,確率の初等的な話題も合わせて丁寧に説明したものである。ただし,細部の数学的な展開については,Kobayashi & Aoki(2012)に依拠するところが大きい。また,「仮定」で導入したモデルは,Henrich(2004)自身がその付録部分においてモデルに加えた修正や,Vaesen(2012)による修正などを包括する形で,Henrichのモデルを一部一般化したものである。この一般化されたHenrichモデルにおいては,各個人の持つ技術の水準が従う分布が特定されていないが,特定の分布を仮定すれば個別の特殊モデルになる。Henrich(2004)の本文部分では,個人の分布がガンベル分布の場合が扱われ,付録部分ではロジスティック分布の場合が扱われた。また,Vaesen(2012)は正規分布の場合を扱った。「仮定」の節で扱われているのは,こうした特殊な場合をすべて包摂するという意味で一般化された広義のHenrichモデルである。一方,中間の2節「正の技術成長の条件」と「標準化された技術成長速度」は本稿の理論的核をなす部分であり,イノベーション率の概念を中心とした独自の考察が展開された。
筆者の記憶にあるものに限っても,Henrichモデルに関連して,本稿で取り上げられなかった話題が幾つかある。そのうち特に重要なものは世代重複の効果である。Kobayashi & Aoki(2012)は,文化的Moranモデルという枠組みを用いてHenrichモデルを重複世代に修正したモデルを扱っている。本稿の式(7)や(26)が示すように,離散世代モデルでは人口Nが技術成長速度に与える影響は対数的であるが,Kobayashi & Aoki(2012)の分析によると,文化的Moranモデルにおいては,その影響が線形的になる。つまり,人口が大きいときでも,人口増加が技術成長速度に与える影響は逓減しない(理由については原著における考察を参照されたい)。既存の実験には重複世代を用いたものもあるし(Caldwell & Millen, 2010),ヒトの齢構造の影響を調べることができる重複世代の実験には意義がある。したがって,将来機会を見つけて,重複世代モデルの予測がどのように実験に翻訳されるのかを考察しておくことは有意義であろう。人口仮説やHenrichモデルは学際的な波及効果を持つので,関連する文献は膨大な量に上る。筆者はここ数年Henrichモデルや人口仮説を研究していなかったうえに,本稿は網羅的なレビューを狙いとしたわけではないので,最近の進展で取りこぼしているものが多くあるに違いないことを,ここでお詫びしておく。
Henrich(2004)がその記念碑的な論文を世に出してから,奇しくも今年でちょうど20年になる。Henrich自身はその論文の中で,モデルのパラメータであるαやβの値が各々の具体的な生業技術に対して推定されることを願う旨を短く述べている。筆者が知る限り,現在までその願いが叶えられた例はない。本稿は野外の具体的な事例への適用ではなく,主に実験室あるいはオンライン実験の柔軟性を活用してHenrichモデルの定量的検証を行う方法について考察を行った。統制された人工的な実験による定量的検証は,実現したとしても,関連の研究者から諸手を挙げて歓迎されるようなものではないかもしれない。それでも筆者の意見では,どんな形であれ,モデルの検証において可能な限り定量的な方法を試みることには意義がある。もちろんすべてのモデルについてそれが可能なわけではないし,その必要があるわけでもない。しかし,少なくともこれから新しくモデルを作ったり,実験を計画したりするのであれば,多少無理をしてでも両者の設計をオーバーラップさせておく(つまり条件によっては両者が一致するようにしておく)ことにより,定量的比較が可能になるし,それによって得られるものは大きいと思う。
Henrichモデルにおいては,個人の技術水準が何らかの方法で定量的に評価できると仮定されているが,評価に用いる課題(例えば良い餌場を探索する,捕獲効率の高い狩猟具をデザインするなど)を明示的に記述してはいない。また,技術が学習によって獲得される過程についても,学習アルゴリズムは具体的に記述されておらず,学習の結果得られる技術水準がある分布に従うことを与件としている。一方,近年の累積的文化進化に関する研究においては,Henrichモデルのように背後にある課題の内容や学習のプロセスをブラックボックスとするのではなく,抽象化された課題(例えばネットワーク上での経路探索課題)と特定の学習ルール(ベイズ推論,勾配法,強化学習など)を想定した,より具体性の高い累積的文化進化の数理モデルも熱心に研究されており(Kirby & Tamariz, 2022; Nakata & Takezawa, 2023; Thompson & Griffiths, 2021),本稿の主たる読者にとってはこういったアプローチのほうが親しみやすいかもしれない。そこで,そのような課題や学習プロセスを明示的に記述した「明示型」モデルの意義について,以下で筆者の個人的な見解を手短に述べ,本稿を締めくくることにしよう。
まず,実験データにフィッティングするという用途を考えると,明示型のモデルでは,データにみられる条件間や個人間の差異を,課題の性質を表すパラメータの変化や認知パラメータの個人差に帰することができるという大きな利点がある。ブラックボックス型モデルにも条件間の差や個人差を混合モデルなどにより形式的に組み込むことは可能だろうが,推定されたパラメータに積極的な解釈を与えることは比較的難しいだろう。もちろん明示型モデルがこの恩恵にあずかるためには,実験として実施可能な設定を特殊な場合として含んでいるモデルでなくてはならない。これを保証するためには,先に一つないし複数の実施可能な実験設定を考えてから,それらの実験設定を特殊な場合として包摂するように緩やかな一般化を施したモデルを作るのがよいだろう。
一方,データとのフィッティングを行わず,純粋に理論モデルとして活用する場合,明示型とブラックボックス型は役割に応じて使い分けるべきだろう。言語の構造の進化(Kirby & Tamariz, 2022)のように,研究の主たる関心が学習者の取り組む課題の構造そのものに関わっている場合には,ブラックボックス型では本質をとらえられないことは言うまでもない。逆に,課題の構造や学習における認知的制約の役割に関心がないか,あるいはそういった詳細に依存しない一般的な法則を導きたいならば,ブラックボックス型を用いるのが望ましい。この場合,課題や学習の詳細はかえってモデルを複雑にし,メカニズムの本質を不透明にしてしまうだけでなく,得られた結果の一般性も不当に弱めてしまうだろう。一方で,ブラックボックス型には,「仮定されたブラックボックスの機能を実現できる課題と学習ルールの組み合わせが本当に実在するか」という疑問が往々にして付きまとう。もちろん,ブラックボックス型モデルから導かれた仮説を,実際の被験者を用いた実験により検証すれば,そのような疑問に一つの回答を与えることはできる。しかしながら,実際の実験において確かめることができるのは,通常偏ったサンプルに属する被験者たちが,ごく少数の特殊な条件下でどのように振舞うかということだけである。言ってみれば,可能なすべての課題設定と学習ルールの組み合わせからなる無限に広い空間の全体ないし大部分で成立すると主張された仮説を検証するために,その空間内の数点のみでデータを採取するようなものである。特定のタイプの課題や学習ルールを仮定しつつも,実際の実験より緩やかに一般化されている明示型モデルは,こうしたブラックボックス型モデルと実験の間に横たわる巨大なギャップを橋渡しすることができる。
このように考えれば,明示型とブラックボックス型の両アプローチにはそれぞれの役割があり,相補的に用いられるべきであると言えよう。例えばNakawake & Kobayashi(2024)は,仮想矢尻の累積的文化進化において,次世代の存在が探索と収穫への労力配分に与える影響を調べたものであるが,上述した一般性と具体性のジレンマを緩和するために,(1)課題や学習ルールを特定しない抽象的な解析的モデル,(2)課題と学習ルールを具体性に記述したシミュレーションモデル,(3)被験者を用いた実験室実験の3点セットを一つの研究として発表している。筆者は,今後文化進化の研究でこうした「3層アプローチ」が積極的に活用されれば,理論と実験の連携はより建設的な方向へ深まっていくだろうと期待している。
ここでは,同じ母集団から独立にサンプリングされたサイズNの標本があるとき,標本中の最大の値の期待値がサンプルサイズNの増加関数になることを証明する。母集団の累積分布関数をF(x),サイズNのサンプルの最大値をXmaxNで表すことにすると,XmaxNの累積分布関数はFN(x),確率密度関数は(FN(x))′で与えられるので,XmaxNの期待値は次式によって計算できることがわかる。
 | (A1.1) |
さらに再右辺の式に現れる二つの項は部分積分法により,それぞれ
 | (A1.2) |
および
 | (A1.3) |
のように変形できる。ただしここで,累積分布関数の一般的な性質
 | (A1.4) |
を用いた。式(A1.2)および式(A1.3)を式(A1.1)に代入することにより,
 | (A1.5) |
が得られる。したがって,
 | (A1.6) |
であるので,E[XNmax]がNの増加関数であることが確かめられた。また,式(A1.6)式はNの減少関数であるので,E[XNmax]の増加速度はNの増大とともに逓減することがわかる。
ここでは,式(7)を導出する。ある世代tにおける最大の技術水準をzmaxで表そう。極値理論より,各個体の技術水準の分布がガンベルの吸引域に属するならば,集団サイズNが十分に大きいとき,次世代の最大の技術水準は近似的にガンベル分布に従うはずである。そのガンベル分布のパラメータを記号a, bで表すことにしよう。すると,次世代の最大技術水準の累積分布関数G(z)は式(9)で与えられる。累積分布関数G(z)は,当の分布に従うガンベル乱数が値zより小さくなる確率に等しいことに注意されたい。したがって,G(zmax)は,次世代の最大の技術水準が,現世代のそれを超えられない確率,すなわち1−ϕmaxに等しい。よって,式(9)より,次式の関係が成立する。
 | (A2.1) |
上式に式(1)を代入することにより,次式を得る。
 | (A2.2) |
さらに,これをaに関して解くことにより,次式を得る。
 | (A2.3) |
一方,次世代の最大技術水準の期待値は,式(10)で与えられるはずである。よって,次世代と現世代の最大技術水準の差の期待値は,次式で与えられる。
 | (A2.4) |
式(A2.3)を式(A2.4)に代入することにより,
 | (A2.5) |
を得る。また,世代t+1の最大技術水準の標準偏差σmax,t+1は式(12)の平方根で与えられる。
 | (A2.6) |
式(A2.5)の両辺を式(A2.6)で割ることで,標準化された技術成長速度が次式で与えられることがわかる。
 | (A2.7) |
関係式 ,
, ,およびϕが小さいときは−log(1−ϕ)≈ϕが成り立つことを用いると,式(A2.7)が式(7)で近似できることがわかる。
,およびϕが小さいときは−log(1−ϕ)≈ϕが成り立つことを用いると,式(A2.7)が式(7)で近似できることがわかる。
1) 本特集号の企画に招待して下さった豊川航博士,結城雅樹博士,そして編集に携わったすべての方々に感謝致します。また,貴重なコメントを下さった匿名の査読者二名と関連文献についてご助言を下さった中分遥博士に感謝致します。筆者の遅筆により関係者の皆様にご迷惑をおかけしたことをお詫びするとともに,皆様の寛大なご対応に深く御礼申し上げます。