On the length spectrums of Riemann surfaces given by generalized Cantor sets

抄録

For a generalized Cantor set E(ω) with respect to a sequence , we consider Riemann surface and metrics on Teichmüller space T(X_E(ω)) of X_E(ω). If E(ω) = (the middle one-third Cantor set), we find that on 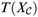, Teichmüller metric d_T defines the same topology as that of the length spectrum metric d_L. Also, we can easily check that d_T does not define the same topology as that of d_L on T(X_E(ω)) if sup q_n = 1. On the other hand, it is not easy to judge whether the metrics define the same topology or not if inf q_n = 0. In this paper, we show that the two metrics define different topologies on T(X_E(ω)) for some such that inf q_n = 0.