2013 Volume 2 Issue Special_Issue Pages S0009
2013 Volume 2 Issue Special_Issue Pages S0009
Accurate mass measurement requires the highest possible mass resolution, to ensure that only a single elemental composition contributes to the mass spectral peak in question. Although mass resolution is conventionally defined as the closest distinguishable separation between two peaks of equal height and width, the required mass resolving power can be ∼10× higher for equal width peaks whose peak height ratio is 100 : 1. Ergo, minimum resolving power requires specification of maximum dynamic range, and is thus 10–100× higher than the conventional definition. Mass resolving power also depends on mass-to-charge ratio. Mass accuracy depends on mass spectral signal-to-noise ratio and digital resolution. Finally, the reliability of elemental composition assignment can be improved by resolution of isotopic fine structure. Thus, the answer to the question of “how much is enough mass resolving power” requires that one first specify S/N ratio, dynamic range, digital resolution, mass-to-charge ratio, and (if available) isotopic fine structure. The highest available broadband mass resolving power and mass accuracy is from Fourier transform ion cyclotron resonance mass spectrometry. Over the past five years, FT-ICR MS mass accuracy has improved by about an order of magnitude, based on higher magnetic field strength, conditional averaging of time-domain transients, better mass calibration (spectral segmentation; inclusion of a space charge term); radially dispersed excitation; phase correction to yield absorption-mode display; and new ICR cell segmentation designs.
A primary goal in mass spectrometry is to identify an analyte, particularly in the presence of other analytes, based on measurement of ion mass. This paper addresses the question of the minimum mass resolving power required to provide mass accuracy sufficient to assign a unique elemental composition, CcHhNnOoSs…, from measurement of mass spectral peak position. Our treatment focuses on Fourier transform ion cyclotron resonance mass spectrometry,1) because it offers the highest broadband resolution of any mass analyzer. Recent examples include resolution and identification of tens of thousands of monoisotopic elemental compositions from a single mass spectrum of petroleum crude oil2) and unit mass resolution of an intact 147 kDa antibody.3)
Recent improvements in FT-ICR mass resolution and accuracy are conveniently separated into instrumental and data reduction categories. Optimization of the experiment has until now been based on single-ion simulations,1) but may in future be guided by large-scale simulations of the trajectories of up to a million or more ions4–6) as they are injected into an ICR ion trap for subsequent excitation and detection. We begin with experimental advances, and then proceed to software developments.
FT-ICR excitation and detection were originally performed with a cubic cell, with dc “trapping” voltage applied to a pair of opposed axial end cap electrodes, rf excitation voltage applied to one pair of opposed transverse electrodes, and induced rf signal detected on the other pair of opposed transverse electrodes.7) Cubic and tetragonal cells were then replaced by a cylindrical cell,8) with a variety of segmentation configurations designed to approach a three-dimensional axial quadrupolar dc trapping potential, and more spatially uniform excitation and detection electric fields.9,10) The best current performance has been obtained with the cells shown schematically in Fig. 1.11–14) The Tolmachev cell extends an original Gabrielse idea of multiple axial segments to which different dc voltages are applied to produce a nearly quadrupolar trapping potential.15) The Nikolaev “dynamically harmonized” cell relies on ion cyclotron motion itself to average out imperfections in the trapping electric field produced by segmented “leaf” electrodes. The Nikolaev cell has achieved mass resolving power greater than 1,000,000 for bovine serum albumin and 20,000,000 for narrow-band detection of reserpine (m/z 609).16)
FT-ICR mass resolving power is directly proportional to the duration of an undamped time-domain ICR signal, which in turn requires maintenance of tight spatial coherence of an orbiting packet of ions of a given m/z ratio. Large-scale simulations have shown that such spatial coherence requires a minimum number of trapped ions.4) Those same simulations also predict coalescence of the trajectories of ions of closely spaced m/z, as a function of the number of trapped ions.17) Thus, for compositionally complex mixtures containing thousands of different elemental compositions, it may be necessary to average 100 or more FT-ICR mass spectra to achieve the desired signal-to-noise ratio and dynamic range. Finally, ion trajectory simulations are also helping to predict (and rectify) degradation in performance due to imperfect construction/alignment of electrodes,6) magnetic field inhomogeneity,18) choice of excitation waveform, etc.
Sample preparationRussian bitumen was dissolved in toluene to yield a 1 mg/mL stock solution. The sample was further diluted to 0.25 mg/mL with 49 : 49 (v/v) toluene–methanol and 2% formic acid for protonation during positive ion electrospray ionization (ESI).
FT-ICR mass spectrometryA custom-built FT-ICR mass spectrometer13) equipped with a passively shielded 9.4 tesla superconducting horizontal solenoid magnet and an electrically compensated cell,12,13) was used for all experiments. Samples were directly pumped through a fused silica capillary at 0.5 μL/min through a 50 μm i.d. fused silica microESI needle under typical ESI conditions (needle, 2.3 kV; tube lens, 350 V; heated metal capillary current, ∼5.0 A). External quadrupole isolation was performed with an Extrel QC 150 quadrupole mass filter (Pittsburgh, PA) and a custom-built accumulation octopole.19–21) Ions in the accumulation octopole were cooled with helium gas at ∼2 mTorr before transfer to the ICR cell. Initial broadband analysis guided the construction of a 4 Mword, 10 Msample/s time-domain excitation waveform.22,23) The SWIFT waveform was stored in the hard drive of a PC data system prior to loading of both the isolation and broadband excitation waveforms to an arbitrary waveform generator (National Instruments (NI) model PXI 5421) and later amplified for output to the ICR cell. After quadrupole and SWIFT isolation of the initial ion population, the resultant spectrum was acquired after broadband excitation of remaining ions at 96 kHz to 961 kHz at 50 Hz/μs and 378 Vp–p. Time-domain data (8 Mword, low m/z cutoff=211) were routed to a differential preamplifier and ultimately digitized (NI Model PXI 5122) by a Predator data station.23)
For a discrete mass spectrum (see Fig. 2), mass measurement precision may be defined as m/σ(m), in which m is measured mass and σ(m) is the standard deviation for a large number of measurements. Fortunately, under very general conditions, it is possible to predict the precision for a large number of measurements from the signal-to-noise ratio, S/N, of a single measurement, according to Eq. (1):
 | (1) |
in which the constant depends on mass spectral peak shape and is of order one in magnitude.24) In the absence of systematic error (as recently demonstrated for FT-ICR MS,25) mass accuracy is the same as mass precision. The importance of Eq. (1) is that it shows that mass imprecision (which ultimately limits mass accuracy) depends directly on SNR. Thus, SNR must be specified in any report of mass measurement accuracy.
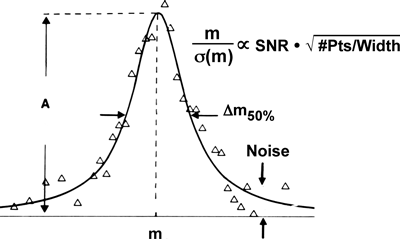
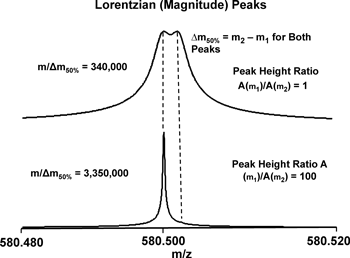
Mass resolution is conventionally defined as the minimum separation between two mass spectral peaks of equal height and width, such that there is a detectable “valley” between them. Mass resolving power is then defined as (m1/(m2−m1)) (Fig. 3, top). Under that definition, mass resolving power (even for a single peak) is m/∆m50%, in which ∆m50% is mass spectral peak full width at half-maximum peak height. However, if (as is almost always the case experimentally) the two peaks are of unequal height, then the minimum mass resolving power to produce a valley between them can be much higher (e.g., ten times higher for a peak height ratio of 100 : 1 (Fig. 3, bottom). The dynamic range for FT-ICR MS peaks can exceed 10,000 : 1, and may be increased by radially dispersed excitation.26) Thus, dynamic range must also be specified in determining the minimal mass resolving power for a particular application.
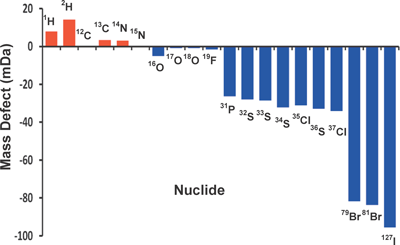
Every isotope of every element has a different mass defect (i.e., the difference between the exact mass of an atom (in Da) and the nearest integer), as shown in Fig. 4 for isotopes of some common elements. Thus, a unique elemental composition may be determined for any molecule from a sufficiently accurate mass measurement.27) For example, a mass resolution of ∼1 mDa suffices to achieve unique elemental composition assignment for essentially all possible elemental compositions, CcHhNnOoSs (as from petroleum crude oil) up to ∼500 Da.28)
As noted above, when direct infusion is available, it is desirable to sum many FT-ICR mass spectra to improve SNR and dynamic range. However, an ionization source may not necessarily produce the same number of ions each time. Because space charge shifts FT-ICR MS peak positions, any variation in ion number will degrade mass measurement accuracy and mass resolving power. We therefore introduced “conditional averaging.” Basically, the idea is to average only those mass spectra whose summed peak heights are the same to within a specified range (say, 10%). It is possible to reduce rms mass error by a factor of 2–3 by such conditional averaging.26)
Mass measurement error may be further reduced by adding a third term to the ICR frequency-to-m/z conversion (mass “calibration”) equation, and (for compositionally complex mass spectra) by separate calibration of multiple mass spectral segments.29) The combination of all of the above data treatments has been shown to reduce rms mass measurement random error to ∼25 ppb, and corresponding systematic error to ∼5 ppb (i.e., essentially negligible).29)
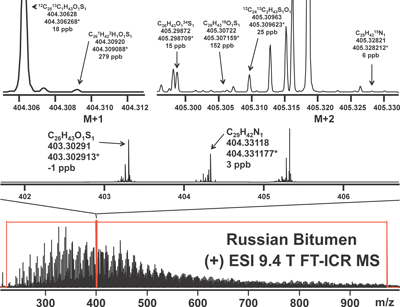
Isotopic fine structure for validation of elemental composition assignmentIt is widely appreciated that the confidence in assigning a monoisotopic elemental composition (mass, M) can be improved by accurate determination of the combined heights of unresolved isotopologue signals at (M+1) and (M+2).30) It is less widely understood that even higher confidence can follow from ultrahigh-resolution mass measurement of individual isotopologues, as shown in Fig. 5. For example, identification of the 34S isotopologue can unequivocally confirm the presence and number of 32S in the monoisotopic species.31)
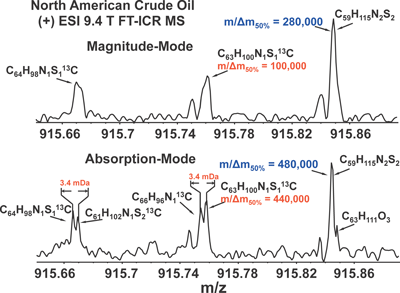
We have recently described broadband phase correction32,33) to yield an absorption-mode FT-ICR mass spectrum, whose resolving power can be up to twice that for conventional magnitude-mode display.34) Moreover, close mass doublets partially or unresolved in magnitude mode may become resolved in absorption mode (see Fig. 6), thereby increasing the number of correctly assigned elemental compositions. Thus, the improvement in resolution based on absorption-mode display is not only quantitative; it can be qualitative (i.e., being able to assign a peak or not). Finally, the improvement due to phase correction is much greater near the baseline of the peak, where (e.g.) a Lorentzian magnitude-mode peak can be ten-fold wider than for absorption mode.
This work was supported by the National Science Foundation (DMR-06-54118; CHE-1016942; CHE-1019193), the Florida State University Future Fuels Institute, the BP/Gulf of Mexico Research Initiative, and the State of Florida.