Growth Behavior of Compounds during Reactive Diffusion in the Solid-Cu/Liquid-Sn System

Abstract

Semi-infinite Cu/Sn diffusion couples prepared by an isothermal bonding technique were used to examine experimentally the kinetics of reactive diffusion in the solid-Cu/liquid-Sn system. Isothermal annealing of the diffusion couple was conducted in the temperature range of T = 753–793 K for various periods up to t = 144 ks (40 h). Owing to annealing, an intermetallic layer composed of ε-Cu₃Sn with scallop morphology and δ-Cu₄Sn with rather uniform thickness is formed at the original Cu/Sn interface in the diffusion couple. The total thickness of the intermetallic layer is proportional to a power function of the annealing time, and the exponent of the power function is close to unity at all the annealing temperatures. Such a power relationship holds also for the ε-Cu₃Sn scallop and the δ-Cu₄Sn layer. This means that volume diffusion controls the growth of the ε-Cu₃Sn scallop and the morphology of the Cu₃Sn/Sn interface influences the rate-controlling process. In contrast, the growth of the δ-Cu₄Sn layer is governed by the interface reaction at the moving Cu₄Sn/Cu interface. Adopting a mean value of 0.87 for the exponent, we obtain a value of 129 kJ/mol for the activation enthalpy of the intermetallic growth.

1. Introduction

In the electronics industry, Cu-base alloys are widely used as conductor materials owing to high electrical conductivity, and various Sn-base alloys are preferentially utilized as Pb-free solders due to low melting temperatures. At the joint between the Cu-base conductor and the Sn-base solder, an intermetallic layer consisting of Cu₆Sn₅ and Cu₃Sn is formed during soldering and then gradually grows during energization heating at solid-state temperatures.^1–11) Since such an intermetallic layer is brittle and possesses high electrical resistivity, the intermetallic growth edgingly deteriorates the mechanical and electrical properties of the joint.

The reactive diffusion in the solid-Cu/liquid-Sn system was observed at a temperature of T = 553 K by Bartels et al.¹²⁾ using Cu/Sn/Cu diffusion couples prepared by an isothermal solidification technique. This technique was used also by Li et al.¹³⁾ to observe the reactive diffusion at temperatures of T = 533, 573 and 613 K. Both observations indicate that an intermetallic layer composed of Cu₆Sn₅ and Cu₃Sn is produced at the original Cu/Sn interface in the diffusion couple in the early stages and Sn and Cu₆Sn₅ are finally depleted in the late stages.^12,13) In contrast, an immersion technique was used by Takaku et al.¹⁴⁾ to observe the reactive diffusion at temperatures of T = 523 and 573 K. According to their observation,¹⁴⁾ an intermetallic layer consisting of Cu₆Sn₅ and Cu₃Sn is also formed at the original Cu/Sn interface in the diffusion couple during annealing, where the thickness of the Cu₃Sn layer is smaller than that of the Cu₆Sn₅ layer. Furthermore, the total thickness of the intermetallic layer is proportional to the square root of the annealing time. Such a relationship is usually called a parabolic relationship. However, the proportionality coefficient of parabolic relationship is greater at longer annealing times than at shorter annealing times. This means that the growth of the intermetallic layer is accelerated at longer annealing times. Nevertheless, any acceleration mechanisms for the parabolic relationship are not yet known.

The kinetics of reactive diffusion in various solid-metal/liquid-metal systems was experimentally observed using an isothermal bonding (IB) technique in previous studies.^15–19) The IB technique is explained in detail elsewhere.²⁰⁾ In the IB technique, the solid and liquid metals are separately preheated at the same temperature as the isothermal annealing temperature in a vacuum. After sufficiently long preheating, the solid and liquid metals are bonded with each other and then annealed immediately. Thus, unlike an immersion technique, the temperatures of the solid and liquid metals are equivalent and remain constant during preheating, bonding and annealing in the IB technique. For instance, in a previous study,¹⁸⁾ the IB technique was used to observe experimentally the kinetics of reactive diffusion in the solid-Fe/liquid-Sn system. In that experiment, semi-infinite solid-Fe/liquid-Sn diffusion couples were isothermally annealed at temperatures of T = 703–773 K. According to the observation, a compound layer of FeSn₂ with columnar polycrystalline microstructure is formed at the original Fe/Sn interface in the diffusion couple. The mean thickness of the FeSn₂ layer is proportional to a power function of the annealing time. This relationship is designated a power relationship. Here, the exponent of the power function is typically equal to 0.6. Such a vale of the exponent means that the layer growth is controlled by volume diffusion and the morphology of growing FeSn₂ grain affects the power relationship. Thus, the kinetics of reactive diffusion in solid-metal/liquid-metal systems is influenced by the microstructure of compounds. Such influence may contribute to the apparent acceleration for the parabolic relationship.

In the present study, the IB technique was used to examine experimentally the kinetics of reactive diffusion in the solid-Cu/liquid-Sn system. Semi-infinite diffusion couples consisting of pure Cu and Sn specimens were prepared by the IB technique and then isothermally annealed in the temperature range of T = 753–793 K. The microstructure of the annealed diffusion couple was observed in a metallographical manner. The rate-controlling process of the compound growth was discussed on the basis of the observation. The discussion may provide information on the acceleration for the parabolic relationship.

2. Experimental

A commercial polycrystalline rod of pure Cu with diameter of 8 mm and purity higher than 99.9% was cut into columnar specimens with length of 5 mm in a manner similar to a previous study.¹⁵⁾ Each columnar specimen was separately annealed in an evacuated silica capsule at a temperature of 1173 K for a time of 2 h, followed by air cooling without breaking the capsule. The top and bottom flat-surfaces of the annealed columnar specimen were mechanically polished on # 800–4000 emery papers.

Polycrystalline columnar specimens with length of 30 mm were cut from a commercial rod of pure Sn with diameter of 6 mm and purity of 99.9%. Each columnar Sn specimen was encapsulated together with a mechanically polished Cu specimen in an evacuated silica capsule with inner diameter of 8.5 mm. The silica capsule was isothermally preheated for a time of 1.8 ks (0.5 h) in the temperature range between 753 K and 793 K. During preheating, the solid Cu specimen was separated from the Sn melt in the silica capsule. After preheating, a flat surface of the solid Cu specimen was immediately contacted with that of the Sn melt with diameter of 8.5 mm and length of 15 mm to prepare a columnar solid-Cu/liquid-Sn diffusion couple.²⁰⁾ The solid/liquid diffusion couple was isothermally annealed for various times up to 144 ks (40 h) at the same temperature as preheating, followed by water quenching with breaking the capsule. The annealing temperature and time are denoted by T and t, respectively.

Emery papers of # 800–4000 were used to polish mechanically cross-sections of the annealed diffusion couple, and then alumina with diameters of 1 μm, 0.3 μm and 0.05 μm was utilized to finish the cross-sections. The microstructure of the cross-section was observed by differential interference contrast optical microscopy (DICOM). Concentrations of Cu and Sn in each phase on the cross-section were measured by electron probe microanalysis (EPMA) using pure Cu and Sn with purity of 99.99% as standard specimens under the following conditions: the accelerating voltage was 20 kV; the probe current was 5 nA; the analyzing crystals for Cu-K_α and Sn-L_α were lithium fluoride (LiF) and polyethylene terephthalate (PET), respectively; and the chemical composition was evaluated by a standard ZAF correction technique.

3. Results and Discussion

3.1 Microstructure

Typical cross-sectional microstructure of the annealed diffusion couple is shown in Fig. 1. Figure 1 indicates a DICOM image of a diffusion couple with T = 773 K and t = 72 ks (20 h). In this DICOM image, the lower and upper regions are the Cu and Sn specimens, respectively. As can be seen, a layer composed of two phases with different contrasts and shapes is observed between the Cu and the Sn. To identify each phase, concentration profiles of Cu and Sn across the two-phase layer along the direction normal to the original Cu/Sn interface were measured by EPMA. A result of the EPMA measurement is indicated in Fig. 2. This figure represents the result of a diffusion couple with T = 753 K and t = 144 ks (40 h). In Fig. 2, the vertical and horizontal axes show the mol fraction y_i of component i and the distance x, respectively, and open circles and squares indicate the mol fractions y_Cu and y_Sn, respectively. Here, the origin x = 0 of the distance is located in the Cu. For the EPMA measurement, however, attention was focused on phase identification of the two-phase layer. Consequently, the location of the origin is merely discretionally chosen to represent conveniently the concentration profiles. As can be seen, the phase with scallop morphology on the Sn side is ε-Cu₃Sn, and that with rather uniform thickness on the Cu side is δ-Cu₄Sn. A recent phase diagram in the binary Cu–Sn system provides that ε-Cu₃Sn and δ-Cu₄Sn are the stable compounds at T = 753–793 K.²¹⁾ Thus, all the stable compounds are produced in the diffusion couple. Such microstructure was recognized in all the annealed diffusion couples. The length of the untransformed Cu specimen in the annealed diffusion couple was compared with the initial length of the corresponding Cu specimen. According to the comparison, salient parts of the ε-Cu₃Sn scallop grow into the Sn, but the two-phase layer rather totally advances towards the Cu. Hereafter, the two-phase layer is merely called the intermetallic layer.

Fig. 1

Cross-sectional DICOM image of the Cu/Sn diffusion couple annealed at T = 773 K for t = 72 ks (20 h).

Fig. 2

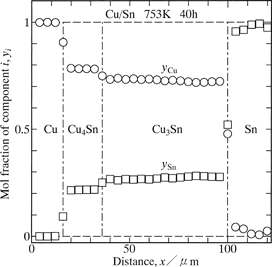
Concentration profiles of Cu and Sn across the intermetallic layer for the Cu/Sn diffusion couple annealed at T = 753 K for t = 144 ks (40 h).

3.2 Growth behavior of intermetallic layer

In cross-sectional DICOM images, such as that shown in Fig. 1, the intermetallic layer consisting of Cu₃Sn and Cu₄Sn is distinguishable from the Cu and the Sn. Figure 3 shows schematic microstructure of the intermetallic layer on cross-section i. From the DICOM image, the area A_i of the intermetallic layer corresponding to the partial length w_i of the original Cu/Sn interface in Fig. 3 was measured on each cross-section, and then the sums A and w were obtained as¹⁸⁾   

\[A = \sum\limits_{i = 1}^{m} A_i \](1a)

and   

\[w = \sum\limits_{i = 1}^{m} w_i \](1b)

from A_i and w_i, respectively, where $m \ge 5$. Using the values of A and w, the total thickness l of the intermetallic layer was evaluated at each annealing time t by the following equation:¹⁸⁾   

\[l = \frac{A}{w}.\](2)

The results for T = 753, 773 and 793 K are indicated as open rhombuses, squares and circles, respectively, in Fig. 4. In this figure, the vertical and horizontal axes show the thickness l and the annealing time t, respectively. Here, both axes are indicated in logarithmic scales. As can be seen, the experimental points are located well on a straight line at each annealing temperature. This means that l is expressed as a power function of t by the following equation.   

\[l = k \left( \frac{t}{t_0} \right)^n\](3)

Here, t₀ is unit time, 1 s. It is adopted to make the argument t/t₀ of the power function dimensionless. The proportionality coefficient k has the same dimension as the thickness l, but the exponent n is dimensionless. As pointed out in previous studies,^18,19) the dimensionless argument of the power function is essentially important; otherwise the dimension of k varies depending on the value of n. From the experimental points in Fig. 4, k and n were evaluated by the least-squares method as shown with various straight lines. The evaluated values are indicated in Fig. 4. According to the evaluation at T = 753–793 K, the overall growth rate of the intermetallic layer monotonically increases with increasing annealing temperature T.

Fig. 3

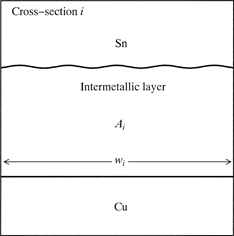
Schematic of morphology for the intermetallic layer on cross-section i.

Fig. 4

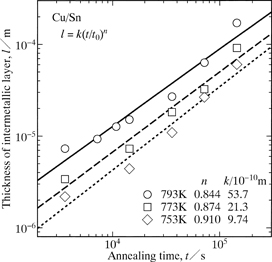
The total thickness l of the intermetallic layer versus the annealing time t at T = 753, 773 and 793 K shown as open rhombuses, squares and circles, respectively.

According to Fig. 1, the interface between the Cu₃Sn scallop and the Cu₄Sn layer is well distinguishable. From DICOM images, such as that shown in Fig. 1, the mean thickness l_i of each compound was evaluated using the relationships similar to eqs. (1a), (1b) and (2). Thus, there exists the following relationship among l₁, l₂ and l.   

\[l = l_1 + l_2\](4)

Here, l₁ is the mean thickness of the ε-Cu₃Sn scallop, and l₂ is that of the δ-Cu₄Sn layer. The values of l, l₁ and l₂ for T = 793 K are plotted against the annealing time t as open circles, squares and rhombuses, respectively, in Fig. 5. In Fig. 5, like Fig. 4, the vertical and horizontal axes indicate the logarithms of l_i and t, respectively, and the open symbols lie well on a straight line for each compound. Therefore, we consider that l_i is expressed as a power function of t by the following equation of the same formula as eq. (3).   

\[l_i = k_i \left( \frac{t}{t_0} \right)^n\](5)

From the experimental points in Fig. 5, k_i and n for l_i in eq. (5) were evaluated by the least-squares method as shown with various straight lines. The evaluated values are indicated in Fig. 5. Since the open squares and rhombuses are slightly scattered, the difference in the growth rate between the Cu₃Sn scallop and the Cu₄Sn layer cannot be conclusively estimated from the result in Fig. 5.

Fig. 5

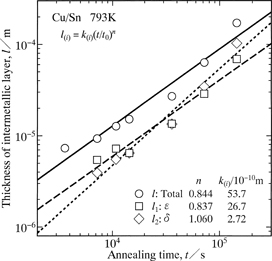
The thicknesses l, l₁ and l₂ versus the annealing time t shown as open circles, squares and rhombuses, respectively, at T = 793 K.

3.3 Rate-controlling process

The mean vales of n for l, l₁ and l₂ are plotted as open circles with error bars in Fig. 6. As can be seen, n is greater than 0.5 and close to unity. When the layer growth is controlled by volume diffusion, n is equal to 0.5.^22–31) Such a relationship is called the parabolic relationship as mentioned earlier. For precipitation of a second phase into an untransformed matrix in binary alloy systems, the growth of the second phase controlled by volume diffusion usually obeys the parabolic relationship. If the shape of the second phase is a paraboloid of revolution or a parabolic cylinder, however, the longitudinal growth of the second phase occurs according to the linear relationship even for the diffusion rate-controlling process.^32–36) Here, the linear relationship means that the length of the second phase linearly increases in proportion to the annealing time. As shown in Fig. 6, n is greater than 0.5 and rather close to unity for the ε-Cu₃Sn scallop. According to the DICOM image in Fig. 1, the Cu₃Sn/Sn interface is gathered considerably. For the precipitation mentioned above, diffusion of solute atoms occurs in the untransformed matrix towards the second phase. On the other hand, for the migration of the Cu₃Sn/Sn interface, diffusion of Cu atoms takes place in the ε-Cu₃Sn scallop and the molten Sn across the Cu₃Sn/Sn interface. However, the diffusion rate is much greater in the molten Sn than in the ε-Cu₃Sn scallop. Consequently, the diffusion in the molten Sn predominates in the migration behavior of the Cu₃Sn/Sn interface and thus the growth behavior of the ε-Cu₃Sn scallop. Here, the molten Sn and the ε-Cu₃Sn scallop correspond to the untransformed matrix and the second phase, respectively, for the precipitation. The value of n close to unity indicates that the growth of the ε-Cu₃Sn scallop is controlled by volume diffusion and affected by the gathered morphology of the Cu₃Sn/Sn interface. Influence of the interface morphology on the value of n is extensively discussed in a previous study.¹⁸⁾ On the other hand, unlike the Cu₃Sn/Sn interface, the Cu₄Sn/Cu₃Sn and Cu/Cu₄Sn interfaces are relatively smooth as indicated in Fig. 1. Hence, the contribution of the interface morphology to the value of n may be negligible for the growth of the δ-Cu₄Sn layer. Nevertheless, as shown in Fig. 6, n is close to unity also for the δ-Cu₄Sn layer. If interface reaction governs the layer growth, n is equivalent to unity.^37–50) As previously mentioned, the δ-Cu₄Sn layer grows mainly into the Cu. Thus, the migration rate is greater for the Cu/Cu₄Sn interface than for the Cu₄Sn/Cu₃Sn interface. Consequently, the interface reaction at the moving Cu/Cu₄Sn interface controls the growth of the δ-Cu₄Sn layer. Since n is close to unity for both l₁ and l₂, it becomes approximately unity also for l as indicated in Fig. 6.

Fig. 6

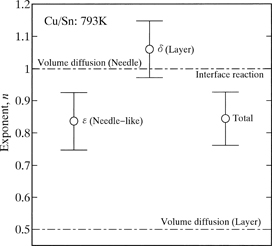
The exponent n for l, l₁ and l₂ at T = 793 K.

The values of n for l are plotted against the annealing temperature T as open circles with error bars in Fig. 7. As can be seen, n is rather insensitive to T. Considering an equivalent value of n at all the annealing temperatures, k and n were simultaneously evaluated from the experimental points in Fig. 4 by the least-squares method. The evaluated value of n is shown as a solid circle with error bars in Fig. 7, and those of k are plotted against T as open circles with error bars in Fig. 8. In Fig. 8, the vertical axis indicates the logarithm of k, and the horizontal axis shows the reciprocal of T. As can be seen in Fig. 8, the open circles are located well on a straight line within experimental uncertainty, and hence the dependence of k on T is expressed by the following equation.   

\[k = k_0 \exp \left( - \frac{Q_k}{RT} \right)\](6)

Here, k₀ is the pre-exponential factor, Q_k is the activation enthalpy, and R is the gas constant. The values of k₀ and Q_k were evaluated from the open circles by the least-squares method as shown with a solid line in Fig. 8. The evaluation provides Q_k = 129 kJ/mol. This value of Q_k corresponds to the activation enthalpy for the intermetallic growth controlled by the volume diffusion with needle-like morphology of ε-Cu₃Sn and the interface reaction with layer morphology of δ-Cu₄Sn.

Fig. 7

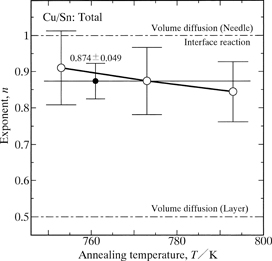
The exponent n for l versus the annealing temperature T.

Fig. 8

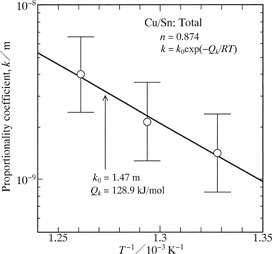
The proportionality coefficient k versus the annealing temperature T.

4. Conclusions

To examine the kinetics of reactive diffusion in the solid-Cu/liquid-Sn system, semi-infinite Cu/Sn diffusion couples were prepared by the isothermal bonding technique and then immediately annealed for various periods at temperatures of T = 753–793 K. At these temperatures, ε-Cu₃Sn and δ-Cu₄Sn are the stable intermetallic compounds in the binary Cu–Sn system.²¹⁾ During annealing, the intermetallic layer consisting of the Cu₃Sn scallop and the Cu₄Sn layer is produced at the original Cu/Sn interface in the diffusion couple. The mean thicknesses of the Cu₃Sn scallop and the Cu₄Sn layer increase in proportion to a power function of the annealing time at T = 793 K. Here, the exponent n of the power function is close to unity. Such a power relationship holds also between the total thickness of the intermetallic layer and the annealing time at T = 753–793 K. If growth of a compound layer is governed by interface reaction, n is equal to unity. Furthermore, the value n = 1 is realized also for the growth of a needle-like compound controlled by volume diffusion. Thus, the growth of the Cu₃Sn scallop is governed by volume diffusion, but that of the Cu₄Sn layer is controlled by interface reaction.

Acknowledgements

The authors are grateful to Dr. Y. Tanaka at Tokyo Institute of Technology, Japan, for stimulating discussions. The present study was partially supported by a Grant-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology of Japan.

REFERENCES

• 1)  L. Zakraysek: Weld. Res. Supplement (Nov.) 536 (1972) 536–541.
• 2)  K.N. Tu: Acta Metall. 21 (1973) 347–354. 10.1016/0001-6160(73)90190-9
• 3)  M. Onishi and H. Fujibuchi: Trans. JIM 16 (1975) 539–547. 10.2320/matertrans1960.16.539
• 4)  H.N. Keller: IEEE Trans. Compon. Hybrids. Manuf. Tech. CHMT-2 (1979) 180–195. 10.1109/TCHMT.1979.1135443
• 5)  H.N. Keller and J.M. Morabito: Surf. Interface Anal. 3 (1981) 16–22. 10.1002/sia.740030108
• 6)  J.O.G. Parent, D.D.L. Chung and I.M. Bernstein: J. Mater. Sci. 23 (1988) 2564–2572. 10.1007/BF01111916
• 7)  A.J. Sunwoo, J.W. Morris, Jr. and G.K. Lucey, Jr.: Metall. Trans., A, Phys. Metall. Mater. Sci. 23A (1992) 1323–1332. 10.1007/BF02665064
• 8)  P.T. Vianco, P.F. Hlava and A.L. Kilgo: J. Electron. Mater. 23 (1994) 583–594. 10.1007/BF02653343
• 9)  D.R. Frear and P.T. Vianco: Metall. Trans., A, Phys. Metall. Mater. Sci. 25A (1994) 1509–1523. 10.1007/BF02665483
• 10)  S. Choi, T.R. Bieler, J.P. Lucas and K.N. Subramanian: J. Electron. Mater. 28 (1999) 1209–1215. 10.1007/s11664-999-0159-y
• 11)  T. Takenaka, S. Kano, M. Kajihara, N. Kurokawa and K. Sakamoto: Mater. Sci. Eng. A 396 (2005) 115–123. 10.1016/j.msea.2005.01.025
• 12)  F. Bartels, J.W. Morris, G. Dalke and W. Gust: J. Electron. Mater. 23 (1994) 787–790. 10.1007/BF02651374
• 13)  J.F. Li, P.A. Agyakwa and C.M. Johnson: Acta Mater. 59 (2011) 1198–1211. 10.1016/j.actamat.2010.10.053
• 14)  Y. Takaku, X.J. Liu, I. Ohnuma, R. Kainuma and K. Ishida: Mater. Trans. 45 (2004) 646–651. 10.2320/matertrans.45.646
• 15)  Y. Tanaka, M. Kajihara and Y. Watanabe: Mater. Sci. Eng. A 445–446 (2007) 355–363. 10.1016/j.msea.2006.09.047
• 16)  Y. Tanaka and M. Kajihara: Mater. Trans. 50 (2009) 2212–2220. 10.2320/matertrans.M2009128
• 17)  Y. Tanaka and M. Kajihara: J. Mater. Sci. 45 (2010) 5676–5684. 10.1007/s10853-010-4633-y
• 18)  M. Hida and M. Kajihara: Mater. Trans. 53 (2012) 1240–1246. 10.2320/matertrans.M2012060
• 19)  A. Nakane, T. Suzuki, M. O and M. Kajihara: Mater. Trans. 57 (2016) 838–845. 10.2320/matertrans.MD201510
• 20)  M. Kajihara and Y.Tanaka: Japanese Patent, Registration No. 5278995 (2013).
• 21)  T.B. Massalski, H. Okamoto, P.R. Subramanian and L. Kacprzak: Binary Alloy Phase Diagrams, vol. 2 (ASM International, Materials Park, OH, 1990) p. 1482.
• 22)  M. Kajihara: Acta Mater. 52 (2004) 1193–1200. 10.1016/j.actamat.2003.10.047
• 23)  M. Kajihara: Mater. Sci. Eng. A 403 (2005) 234–240. 10.1016/j.msea.2005.05.013
• 24)  M. Kajihara: Mater. Trans. 46 (2005) 2142–2149. 10.2320/matertrans.46.2142
• 25)  M. Kajihara: Defect and Diffusion Forum 249 (2006) 91–96. 10.4028/www.scientific.net/DDF.249.91
• 26)  M. Kajihara: Mater. Trans. 47 (2006) 1480–1484. 10.2320/matertrans.47.1480
• 27)  Y. Tanaka and M. Kajihara: Mater. Trans. 47 (2006) 2480–2488. 10.2320/matertrans.47.2480
• 28)  M. Kajihara and T. Yamashina: J. Mater. Sci. 42 (2007) 2432–2442. 10.1007/s10853-006-1212-3
• 29)  M. Kajihara: Mater. Trans. 49 (2008) 715–722. 10.2320/matertrans.MRA2007316
• 30)  M. Kajihara: Mater. Trans. 51 (2010) 1242–1248. 10.2320/matertrans.M2010075
• 31)  M. Kajihara: Mater. Trans. 53 (2012) 1896–1904. 10.2320/matertrans.M2012161
• 32)  A. Papapetrou: Z. Kristallogr. 92 (1935) 89–130.
• 33)  G.P. Ivantsov: Dokl. Akad. Nauk SSSR 58 (1947) 567–569.
• 34)  G. Horvay and J.W. Cahn: Acta Metall. 9 (1961) 695–705. 10.1016/0001-6160(61)90008-6
• 35)  R. Trivedi: Acta Metall. 18 (1970) 287–296. 10.1016/0001-6160(70)90143-4
• 36)  P.E.J. Rivera-Diaz-del-Castillo and H.K.D.H. Bhadeshia: Mater. Sci. Technol. 17 (2001) 25–29. 10.1179/026708301101509070
• 37)  Y. Yamamoto and M. Kajihara: Mater. Trans. 42 (2001) 1763–1770. 10.2320/matertrans.42.1763
• 38)  Y. Muranishi and M. Kajihara: Mater. Sci. Eng. A 404 (2005) 33–41. 10.1016/j.msea.2005.05.044
• 39)  T. Hayase and M. Kajihara: Mater. Sci. Eng. A 433 (2006) 83–89. 10.1016/j.msea.2006.06.039
• 40)  K. Mikami and M. Kajihara: J. Mater. Sci. 42 (2007) 8178–8188. 10.1007/s10853-007-1700-0
• 41)  Y. Yamamoto and M. Kajihara: J. Electron. Mater. 37 (2008) 1710–1720. 10.1007/s11664-008-0535-z
• 42)  M. Kajihara and Y. Tejima: J. Phys.: Conf. Ser. 165 (2009) 012091, 1–4.
• 43)  Y. Tejima, S. Nakamura and M. Kajihara: J. Mater. Sci. 45 (2010) 919–928. 10.1007/s10853-009-4021-7
• 44)  M. O and M. Kajihara: Mater. Trans. 52 (2011) 677–684. 10.2320/matertrans.M2010433
• 45)  M. O, Y. Takamatsu and M. Kajihara: Mater. Trans. 55 (2014) 1058–1064. 10.2320/matertrans.M2014023
• 46)  M. Hashiba, K. Masui and M. Kajihara: Mater. Trans. 56 (2015) 30–39. 10.2320/matertrans.M2014202
• 47)  M. Nakayama and M. Kajihara: Mater. Trans. 56 (2015) 798–802. 10.2320/matertrans.M2015059
• 48)  Y. Takamatsu, M. O and M. Kajihara: Mater. Trans. 58 (2017) 16–22. 10.2320/matertrans.M2016278
• 49)  M. Nakayama, M. O and M. Kajihara: Mater. Trans. 58 (2017) 561–566. 10.2320/matertrans.M2016409
• 50)  Y. Takamatsu, M. O and M. Kajihara: Mater. Trans. 58 (2017) 567–573. 10.2320/matertrans.M2016416