Evaluation of Fatigue Crack Propagation Behavior of Pressurized Sintered Ag Nanoparticles and Its Application to Thermal Fatigue Life Prediction of Sintered Joint

Abstract

Fatigue crack propagation rate of pressure-sintered Ag nanoparticles was investigated and prediction method of fatigue crack propagation using strain energy density computed by FEM was proposed. The fatigue crack propagation rate was lower than that of pressureless-sintered Ag nanoparticles around ambient temperature. At high temperature, multiple small cracks occurred ahead of a main crack and they were connected with one another and the propagation rate of the main crack increased, so that properties of fatigue crack propagation in the high temperature region were close to those of pressureless-sintered Ag nanoparticles.

As the inelastic strain energy density and the length of its acquisition area were inversely proportional, the prediction of fatigue crack propagation that do not depend on the size of the area was possible by the use of the proportional constant of the relationship. The behavior of thermal fatigue crack propagation of sintered joint structure that was predicted by the derived fatigue crack propagation law was mostly in agreement with experimental behavior.

Fig. 7 Relationships between fatigue crack propagation rate and ΔW_in.

1. Introduction

Next generation power devices that use wide-bandgap semiconductors are expected to operate at much higher temperatures than conventional devices. Using lead free solder alloys as die attach materials for power devices that operate at high temperatures is difficult in view of the mechanical reliability. In the circumstance, sinter joining with Ag nanoparticles is now considered as a potential alternative to conventional solder alloys.^1,2) There have been, however, a few research reports released to the present on mechanical reliability of sintered Ag nanoparticles and there still remain many unclear points about the reliability. Recently, static characteristics of Ag nanoparticles are now being investigated through shearing tests of joint specimens^3–5) or mechanical tests with the use of film type specimens.^6–8)

As for investigations on characteristics of fatigue crack propagation and fatigue crack propagation law, there are no reports available yet except for the authors’ recent research. These are essential in studying the reliability of power semiconductor devices. The author et al. have investigated the rate of fatigue crack propagation of pressureless-sintered Ag nanoparticles with the use of cyclic J-integral ΔJ,⁹⁾ a fracture mechanics parameter, and have demonstrated that fatigue properties of Ag nanoparticles are largely different from those of solder alloys.¹⁰⁾ Given the prediction of the fatigue life of a power semiconductor device, it is not easy to calculate ΔJ in real device structure. A parameter alternative to ΔJ for assessing fatigue crack propagations is necessary. A method that do not use fracture mechanics parameters was proposed for BGA joints; in the method, FEM is used to calculate the inelastic strain energy density range ΔW_in in the neighborhood of the fatigue crack tip region and the failure life is evaluated.^11,12) Although there are points to note in the proposed method, such as its dependence of ΔW_in on the mesh size of FEM model, the calculation of ΔW_in is easier with the method than with ΔJ. In addition, considering the thermal fatigue analysis in die attach materials, a parameter applicable to the creep region is necessary. Since ΔW_in can be applied not only to the fatigue analysis in elasto-plastic region but also to the analysis in creep region, ΔW_in is suitable as the parameter for the thermal fatigue analysis of die attach materials. The author et al. have evaluated the fatigue crack propagation properties of pressureless-sintered Ag nanoparticles by the use of the inelastic strain energy density range and demonstrated its brittleness in the combination of the strain energy concentration present inside the pores of the sintered material with the low quality grain boundaries. For the future practical application of Ag nanoparticles to die attach materials, research of pressure-sintering that is deemed to have more ductile mechanical properties is required.

Therefore, in this study, fatigue crack propagation properties of pressure-sintered Ag nanoparticles that are expected to have more ductile was evaluated using strain energy density. And then, with the use of the derived fatigue crack propagation law, the thermal fatigue crack propagation life of a sintered joint specimen was predicted.

2. Experimental Procedure

2.1 Specimen

Ag nanoparticle paste with an average diameter of 100 nm was used. The paste was sintered at 523 K under a pressure of 5 MPa to create a strip-shaped plate material. The plate was then machined into a miniature sized flat plate specimen with a single notch (Single-Edge Notched) as in Fig. 1.^10,13) The notch was introduced by a precision wire saw (50 µm in wire diameter).

Fig. 1

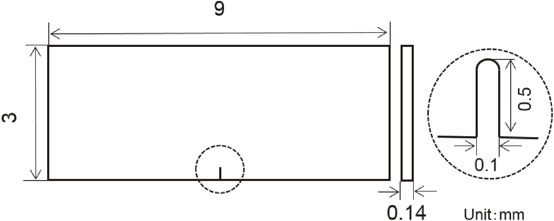
Schematic illustration of single-edge notched (SEN) specimen.

2.2 Fatigue crack propagation test

The fatigue crack propagation test was performed in displacement-controlled pulsating tensile-tensile mode.¹³⁾ The control waveform was symmetric triangular wave. The total displacement range was 4 µm–15 µm (equivalent to the nominal strain range 0.13%–0.50%). Test temperatures were three levels of 298 K, 333 K, and 448 K. The strain rate was 1 × 10⁻³/sec. A fatigue crack propagation machine was a fatigue test machine equipped with a piezo actuator (Saginomiya: LMH-207-20) as in Fig. 2. For measuring displacements, a capacitive displacement sensor installed near the specimen fixing jig was used; the values measured by the sensor were used for actuator controlling. Specimen temperature was raised by the ceramic heater installed inside a specimen fixing jig and test temperatures were controlled by the thermocouple fixed to the specimen fixing jig with the allowable range of ±2 K. Fatigue crack lengths were measured by video images recorded at each prescribed cycles by a microscope (Leica Z16 APO) installed on the upper part of the test machine.

Fig. 2

Fatigue crack propagation testing machine.

2.3 Evaluation of fatigue crack propagation rate

In the test conditions of the large scale yielding, like this study, it is ideal to evaluate of the fatigue crack propagation using path-independent cyclic J-integral ΔJ. However, as it is difficult to calculate ΔJ by general purpose FEM code, assessment with a scalar parameter alternative to ΔJ is required. The author et al. have so far made the evaluation of fatigue crack propagation of pressureless-sintered Ag nanoparticles by the use of the inelastic energy density range ΔW_in around the crack tip calculated by FEM as a scalar parameter alternative to ΔJ.¹³⁾ This method is based on the assumption that the average of inelastic strain energy densities near the crack tip is representative of the mechanical environment of the region where damage is progressing in front of the crack tip. The calculation of ΔW_in was carried out at the element group contained in the region surrounding the crack tip of FEM model, elemental solutions of inelastic strain energy densities were averaged to calculate the quantity of variation per fatigue cycle. The equation to calculate the average of element solutions is shown in eq. (1).¹¹⁾   

\begin{equation} \Delta W_{\text{in}} = \frac{\displaystyle\sum \Delta W_{\text{in}}^{\text{element}} \cdot V^{\text{element}} }{\displaystyle\sum V^{\text{element}}} \end{equation} (1)

where $\Delta W_{\text{in}}^{\text{element}}$ is the elemental solution of the variation quantity of inelastic strain energies, and V^element is the cubic volume per element. A FEM model was created for each the crack length reached a predetermined size to calculate ΔW_in, and from the relationship between fatigue crack propagation rate and ΔW_in, a fatigue crack propagation law of Paris type was derived.¹³⁾ The FEM models was 1/2 symmetric with a notch introduced as in Fig. 3. The element type was quadrilateral eight-node plane stress element. The solver used was general purpose code ANSYS ver. 17.2. The area for performing the calculation of ΔW_in had four sides with 20 µm/side with the crack tip at the center. And in the area, tetragonal meshes with 2 µm × 2 µm were provided. The material property of sintered Ag nanoparticles to be used for FEM analysis was defined as elasto-plastic body. For the plastic constitutive equation, the nonlinear kinematic hardening law (Chaboche model)¹⁴⁾ was used as in eq. (2).   

\begin{equation} \dot{x}_{\text{i}} = \frac{2}{3}\sum_{i = 1}^{n}A_{1} \dot{\varepsilon}_{\text{p}} - A_{2}x_{\text{i}}\dot{p} \end{equation} (2)

where $\dot{x}_{\text{i}}$ is the back stress rate, $\dot{\varepsilon }_{\text{p}}$ is the inelastic strain rate, x_i is the back stress, $\dot{p}$ is cumulative inelastic strain rate, and A₁ and A₂ are the material constants. The material constants for the constitutive equation were determined by inverse analysis on the basis of separately conducted tensile test results so as to reproduce the load-displacement hysteresis loop obtained from individual fatigue crack tests. Representative material constants are shown in Table 1.

Fig. 3

Geometry of Single Edge Notch (SEN) specimen.

Table 1 Representative material constants of Chaboche model for calculating ΔW_in.

2.4 Prediction method of thermal fatigue crack propagation life of sintered joint specimen

Thermal fatigue crack propagation life in the joint structure was predicted by the fatigue crack propagation law gained from the SEN specimen. The specimen was a joint body of SiC and the Cu/CuCr clad that was pressure-sintered with Ag nanoparticles in the same condition as in the fatigue crack propagation testing. A schematic illustration of the joint specimen is shown in Fig. 4. The joint specimen was subjected to thermal cycle testing with the maximum temperature of 448 K and the minimum of 218 K at the temperature ramp rate of 23.0 K/min and with the dwelling time of 15 minutes for each of maximum and minimum temperature. The crack length on the diagonal surface was measured at the number of cycles prescribed by ultrasonic microscope.

Fig. 4

Sintered joint specimen for thermal cycle test.

The elastic modulus, Poisson’s ratio, and CTE of each material used in FEM analysis are shown in Table 2. The property of Ag nanoparticles was defined as elasto-plastic creep body. For the elasto-plastic constitutive equation, Chaboche model was used and Norton’s law of eq. (3) was used for the creep constitutive equation. Material constants of constitutive equations were determined by the tensile test and stress relaxation test that were conducted separately. Determined material constants for Chaboche model of individual equations are shown in Table 3.   

\begin{equation} \frac{d\varepsilon}{dt} = 3.5\times 10^{-4}\sigma^{7.1}\exp\left(-\frac{92000}{8.31\cdot T}\right) \end{equation} (3)

where the units of energy for strain rate, stress and activation energy are s⁻¹, MPa, and KJ/mol respectively.

Table 2 Elastic material constants of each material of sintered joint specimen.

Table 3 FEM model for calculation of ΔW_in.

2.5 Microstructural observation

The microstructure of the specimens were observed by a field emission scanning electron microscope (FE-SEM) following polishing by Ar ion sputter-etching.

3. Results

3.1 Fatigue crack propagation

The microstructure of the SEN specimen after sintering is shown in Fig. 5, where the porous structure specific to sintered Ag nanoparticles was observed. The porosity of the specimen in this study was about 8.3% and an average grain size was 247 nm. It is known that the porosity of sintered Ag nanoparticles is strongly dependent on sintering conditions, according to which the porosity varies from about 10% to 40%.^15–18) In pressureless-sintering, numerous pores were observed in the neck area.^10,17) In comparison with the porosity in pressureless-sintered body, the porosity in the specimen of this study was lower and there were a few of neck areas that were seen in the process of sintering. The microstructure of the specimen in this study was densified because the sintering was progressing by pressurization.

Fig. 5

Initial microstructure of Ag nanoparticles sintered under pressure of 5 MPa.

Figure 6 shows the relationship between fatigue crack length at each test temperature a and the number of cycles N. The relationship between fatigue crack length and the number of cycles became linear at any test temperature. This is because the fatigue crack propagation test in this study was conducted under the displacement controlling mode, in which only small changes took place in the driving forces (ΔW_in) to growth the fatigue crack. Thus, the fatigue crack propagation rate was calculated by the linear approximation of the relationship between fatigue crack length a and the number of cycles N.

Fig. 6

Fatigue crack propagation curves for each condition.

Figure 7 shows the relationship between fatigue crack propagation rate of pressure-sintered Ag nanoparticles and ΔW_in. At any test temperature the fatigue crack propagation law of Paris type holds between fatigue crack propagation rate and ΔW_in. Material constants at individual temperatures are shown in Table 4.   

\begin{equation} \frac{da}{dN} = C_{1}\Delta W_{\text{in}}{}^{C_{2}} \end{equation} (4)

where C₁ and C₂ are the material constants. The units of ΔW_in and da/dN were MJ m⁻³ and m respectively. The fatigue crack propagation rate at 298 K was nearly identical to that at 333 K and the gradient of a straight line C₂ was about 1.0. The C₂ of the pressureless-sintered Ag nanoparticles as reported previously¹³⁾ was 3–5 at ambient temperature, which means C₂ was decreased by pressure-sintering. Although a direct comparison cannot be made, it is reported that the exponent of Dowling-Begley law, which is the fatigue crack propagation law that uses ΔJ, generally shows 1.0–2.0 in steel alloys and solder alloys.^19–22) The C₂ of the fatigue crack propagation law of pressure-sintered Ag nanoparticles was close to that of ductile metals. In a pressureless-sintered Ag nanoparticles, its microstructure became densified with increasing sintering temperature, and as a consequence, fatigue crack propagation resistance improved and C₂ was decreased^10,13) — this is because the sintering further progressed as the sintering temperature was increased and in conjunction with this, pores and neck areas decreased, which led to decrease in the internal stresses concentration areas. Compared with pressureless-sintered Ag nanoparticles, pressure-sintered Ag nanoparticles had a fewer pores and a fewer neck areas, which made the microstructure more densified. This microstructure induced the property of fatigue crack propagation that was close to ductile metals. On the other hand, the fatigue crack propagation rate at 448 K was higher than at 333 K and C₂ was about 1.7 close to the value of the pressureless-sintered Ag nanoparticles. Although the mechanical properties of the pressureless-sintered Ag nanoparticles become ductile by grain boundary diffusion-type creep with increasing temperature and concurrently the rate of fatigue crack propagation decreases,¹³⁾ in the pressure-sintered Ag nanoparticles in this study, the fatigue crack propagation rate increased with an increase in temperature.

Fig. 7

Relationships between fatigue crack propagation rate and ΔW_in.

Table 4 Material constants of fatigue crack propagation law.

Figure 8 shows the fatigue crack propagation path in representative test conditions of pressure-sintered Ag nanoparticles. At any test temperature, a fatigue crack propagated along a grain boundary (the sintered interface between Ag particles). In crystalline materials with a grain size of several hundred nanometers, deformation and fracture at grain boundary become dominant.²³⁾ Because of this, also in pressure-sintered Ag nanoparticles, grain boundary fracture became fatigue crack propagation mechanisms. Pores originally contained in sintered Ag particles become clumped/connected to each other after a long time of high temperature exposure and macroscopic pores grow large which causes for mechanical properties to decrease.¹⁸⁾ The testing time in this study was relatively short for about several to several dozens of hours. However, compared to the initial microstructure, the size and the number of pores increased around a crack tip by stress-induced diffusion as well as temperature. Since the increased pores leads a brittle characteristic from the structural point of view, the fatigue crack propagates through a pore at any test condition.

Fig. 8

SEM micrographs showing microstructures around fatigue crack tip after fatigue test.

When the microstructure after the testing was observed with a focus on changes in fracture mechanisms at 448 K and other temperatures, differences were seen in the damage near a crack tip. As shown in Fig. 8, a grown up crack was seen at 448 K ahead of the main crack (in the traveling direction of the crack). At lower temperatures, however, other cracks except for the main crack were not observed. Grain boundary diffusion became more active at 448 K than at ambient temperature and the pores easily became connected to one another. Connecting of the pores induces crack initiation and multiple small cracks occur ahead of the main crack. It is considered that by the main crack being connected to small cracks, brittle properties were derived and as a result, the fatigue crack propagation rate increased. Thus, C₂ and the fatigue crack propagation rate increased at 448 K.

3.2 Prediction of fatigue crack propagation of sintered joint specimen

The inelastic strain energy density range of the crack tip calculated by FEM is dependent on the size of the area surrounding a crack and dependent on the size of an element in the area, unlike the case in which the path independent J was used. In considering the application of the foregoing to fatigue crack propagation analysis in real joint structures, the dependence of the area surrounding a crack and the dependence of the element size in the area need to be clarified. Therefore, these types of dependence having effects on W_in were investigated by altering the size of the region to obtain inelastic strain energy W_in and the size of the divided element. The FEM models was 1/2 symmetric with a notch introduced as in Fig. 3. Figure 9 shows the relationship between the side length of quadrate L_area to obtain W_in, the element size in the square region L_element and W_in. As shown in Fig. 9, the gradient of the straight line was −1 and W_in is inversely proportional to L_area. Furthermore, even if an alteration is made to L_element, the effect of the element size is almost negligible because W_in is calculated as an average in the quadrate region.

Fig. 9

Relationship between W_in and L_area for each element size (L_element).

If L_area is replaced with the distance from the crack tip, the relationship between L_area and W_in obeys HRR singularity.^24,25) In the HRR singularity field, stress and strain can be found as in eq. (5) and eq. (6).   

\begin{equation} \sigma_{ij} = k_{1}\left(\frac{J}{r}\right)^{\frac{1}{n + 1}}{} \cdot \tilde{\sigma}_{ij}(\theta) \end{equation} (5)

  

\begin{equation} \varepsilon_{ij} = k_{2}\left(\frac{J}{r}\right)^{\frac{n}{n+1}} {}\cdot \tilde{\varepsilon}_{ij}(\theta) \end{equation} (6)

where J is the J-integral, n is the strain hardening exponent, r is the distance from the crack tip, and k₁ and k₂ are the material constants. And σ(θ) and ε(θ) are the constants relating to the angle θ of the polar coordinate with the crack tip and to material. The stress and strain at the crack tip have the relationship of −1/(n + 1) and −n/(n + 1) squared for the distance from the crack tip r and they depend on the strain hardening exponent of the material. It has been mathematically analyzed, however, that in the HRR singularity field, the strain energy density gained from the integration of stress by strain is proportional to 1/r.²⁴⁾ The W_in calculated in this study is an average of the sum of the elemental solutions of strain energy densities obtained from all the elements in the square area surrounding the crack tip. When a sufficiently large plastic deformation is loaded, strain energy density W becomes equivalent to the W_in. Therefore, as long as the acquisition area of W_in is in the HRR singularity field, the following inverse relationship holds between W_in and the length of one side of the acquisition area.   

\begin{equation} W_{\text{in}} = \frac{W_{\text{in-c}}}{L_{\text{area}}} \end{equation} (7)

where W_in-c is the proportional constant. The result in Fig. 9 indicates the relationship of eq. (7). The inverse relationship holds regardless of the types of materials since it is not dependent on the material constant of the elasto-plastic constitutive equation. The author et al. have conducted similar research of pressureless-sintered Ag nanoparticles and confirmed the inverse relationship.¹³⁾ W_in-c is determined by calculating a given L_area. However, W_in-c, which was not dependent on L_area, becomes to have the quality similar to the path-independent of J-integral. And in a sense of physics, W_in-c was close to the J-integral that linear-integrated the strain energy density on the path, since it was the result of multiplying the average of the strain energy density in the acquisition area by the length of the acquisition area. Using this W_in-c enables fatigue crack propagation assessments that are not dependent on L_area and L_element. Therefore, in this study, the fatigue crack propagation law of Paris type was derived with the use of ΔW_in-c and fatigue crack propagation in a joint structure was predicted. Fatigue crack propagation law that uses ΔW_in-c is shown in eq. (8).   

\begin{equation} \frac{da}{dN} = C_{3}\Delta W_{\text{in-c}}{}^{C_{2}} \end{equation} (8)

where C₃ is the material constant, which were determined from the experimental results shown in Fig. 7. The material constants for the fatigue crack propagation law with ΔW_in-c are shown in Table 5. The units of ΔW_in-c and da/dN were N m⁻¹ and m respectively.

Table 5 Material constants for fatigue crack propagation law using ΔW_in-c.

The ΔW_in-c in the sintered joint during temperature cycling was calculated with a two-dimensional FEM model having the reproduced diagonal cross section of the specimen as shown in Fig. 10. The element type was eight-node axisymmetric element. A FEM model was created for each predetermined crack length. Contact elements were set to the fatigue crack surfaces and the fatigue crack propagation path was determined based on the observations made after the thermal cycle test. A SAT (Scanning Acoustic Tomograph) image of and a SEM image of a cross section observed after testing are shown in Fig. 11. The fatigue crack started to develop from the joint interface at the corner on the chip side and propagated near the joint interface adjacent to the clad material. In the FEM, an initial crack of 20 µm was created and the fatigue crack propagation path was set to the joint interface on the side of the clad material. Assuming that the driving force for fatigue crack propagation is dominated by the energy on the side of the sintered layer, ΔW_in was calculated in the area of 10 µm × 20 µm on the side of Ag nanoparticles near a fatigue crack. Assuming in-phase type thermal fatigue, the reference temperature was set to be 298 K. The life of thermal fatigue crack propagation of the joint specimen was calculated by the use of eq. (9) as below.   

\begin{equation} N = \int_{a_{0}}^{a_{\text{f}}}\frac{da}{C_{3}\Delta W_{\text{in-c}}(a)^{C_{2}}} \end{equation} (9)

where ΔW_in-c (a) is the proportional constant of eq. (7) as a function of fatigue crack length, a₀ is the initial crack length, and a_f is the critical fatigue crack length. Thermal cycle testing with three cycles was analyzed and ΔW_in was calculated between the second cycle and the third cycle and then ΔW_in-c was found by eq. (7). In this study, the elasto-plastic creep constitutive equation was used for FEM analysis of the temperature cycling. Since HRR singularity field appeared in the creep singularity field expressed by C^*-integral,^26–28) eq. (7) held. ΔW_in-c was calculated for each predetermined length and a function of ΔW_in-c and fatigue crack length was obtained. Then the function was input into the eq. (9) to obtain the number of cycles taken to reach the individually prescribed crack lengths. For the material constants of eq. (9) to be used for the calculation of fatigue crack propagation life, the fatigue crack propagation law obtained at the test temperature 448 K were used on the assumption that fracture advances on the side of high temperature.

Fig. 10

FEM model of sintered joint specimen for thermal cycle analysis.

Fig. 11

SAT image and SEM micrograph showing crack propagation path of sintered joint specimen after thermal cycle test.

Figure 12 shows the relationship between crack length and ΔW_in-c obtained from the FEM analysis of the thermal cycle test. ΔW_in-c increased as crack length increased, which relationship can be approximated by a quadratic polynomial. By inputting this relational expression in eq. (9), the number of fatigue cycles were obtained at the point where the crack length grew from the initial length to 2.2 mm.

Fig. 12

ΔW_in-c as a function of fatigue crack length for thermal cycle analysis.

Figure 13 shows a comparison between the calculated number of cycles to thermal fatigue crack propagation and results of thermal cycle test. White circles are the test results and the curved line is the calculated value. The prediction results of fatigue crack propagation by the method of the study are roughly consistent with the fatigue crack propagation in the thermal cycle test. However, according to the prediction results, the fatigue crack propagation rate increased with an increase in fatigue crack length, whereas the test results showed that the fatigue crack propagation rate decreased with an increase in fatigue crack length. This may have occurred due to a possible reason that the axisymmetrical model used in the FEM analysis did not precisely reproduce the joint specimen. In the two-dimensional model with axisymmetrical elements, the length of crack front decreases with increasing fatigue crack propagation. Therefore, the load to be subjected to per unit length of the crack front become larger along with crack propagation, resulting in an increase in the fatigue crack propagation rate. On the other hands, the actual structure of the joint body was quadrate. In the case, the crack initiated at the joint corner propagated and the crack length increased along with the advancement of crack propagation. Therefore, the load per unit length of the crack front decreased with a decrease in the fatigue crack propagation rate. It is considered that more precise crack propagation behavior can be reproduced with the use of a three-dimensional FEM model.

Fig. 13

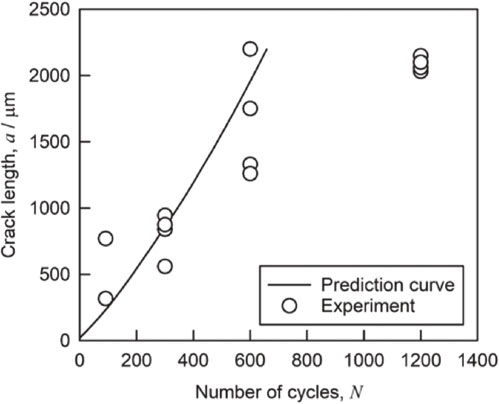
Prediction result of thermal fatigue crack propagation for sintered joint specimen.

4. Conclusion

1. (1)    The fatigue crack propagation rate at 298 K was same as that at 333 K. The rate was lower than the fatigue crack propagation rate of pressureless-sintered Ag nanoparticles. The power exponent of the fatigue crack propagation law was about 1.0, which was smaller than that of pressureless-sintered Ag nanoparticles.
2. (2)    The fatigue crack propagation rate at the test temperature of 448 K was higher than that at the test temperature of 333 K and the exponent of the fatigue crack propagation law was 1.7. Properties of fatigue crack propagation in the high temperature region are close to those of pressureless-sintered Ag nanoparticles.
3. (3)    At the test temperature of 448 K, multiple small cracks occurred ahead of a main crack and they were connected with one another and the propagation rate of the main crack increased. This is thought to be the cause of increases in the fatigue crack propagation rate and the power exponent of the fatigue crack propagation law.
4. (4)    Inelastic strain energy density W_in and the one side length of its acquisition area L_area were inversely proportional. It was become evident that with the use of W_in-c which was the proportional constant of the relationship, the assessment of fatigue crack propagation that do not depend on L_area was possible.
5. (5)    The behavior of thermal fatigue crack propagation of the joint specimen that was predicted by the fatigue crack propagation law of Paris type that used ΔW_in-c was mostly in agreement with experimental value.

Acknowledgments

This research was conducted with the support of the Grants-in-Aid of New Energy and Industrial Technology Development Organization (NEDO).

REFERENCES

• 1)   S.A.  Paknejad and  S.H.  Mannan: J. Microel. Rel. 70 (2017) 1–11.
• 2)   K.S.  Siow and  Y.T.  Lin: ASME J. Electron. Packag. 138 (2016) 020804.
• 3)   M.S.  Kim,  K.  Matsunaga,  Y.H.  Ko,  C.W.  Lee and  H.  Nishikawa: J. Mat. Trans. 57 (2016) 1192–1196.
• 4)   S.A.  Paknejad,  G.  Dumas,  G.  West,  G.  Lewis and  S.H.  Mannan: J. Alloys Compd. 617 (2014) 994–1001.
• 5)   S.T.  Chua and  K.S.  Siow: J. Alloys Compd. 687 (2016) 486–498.
• 6)   G.  Chen,  X.H.  Sun,  P.  Nie,  Y.H.  Mei,  G.Q.  Lu and  X.  Chen: J. Electron. Mater. 41 (2012) 782–790.
• 7)   X.  Chen,  R.  Li,  K.  Qi and  G.Q.  Lu: J. Electron. Mater. 37 (2008) 1574–1579.
• 8)   C.  Chen,  S.  Nagao,  H.  Zhang,  J.  Jiu,  T.  Sugahara,  K.  Suganuma,  T.  Iwashige,  K.  Sugiura and  K.  Tsuruta: J. Electron. Mater. 46 (2017) 1576–1586.
• 9)   N.E.  Dowling: ASTM Spec. Tech. Publ. 601 (1976) 19–32.
• 10)   R.  Shioda,  Y.  Kariya,  N.  Mizumura and  K.  Sasaki: J. Electron. Mater. 46 (2017) 1155–1162.
• 11)   R.  Darveaux: J. Electron. Packag. 124 (2002) 147–154.
• 12)   J.H.  Lau: J. Electron. Packag. 124 (2002) 212–220.
• 13)   R.  Kimura,  Y.  Kariya,  N.  Mizumura and  K.  Sasaki: Mater. Trans. 59 (2018) 612–619.
• 14)   J.L.  Chaboche: Int. J. Plast. 5 (1989) 247–302.
• 15)  S. Okuno, Q. Yu and Y. Nakata: Proc. of IEEE 18th Electronics Packaging Technology Conference, (2016) pp. 488–491.
• 16)   T.  Suzuki,  T.  Terasaki,  Y.  Kawana,  D.  Ishikawa,  M.  Nishimura,  H.  Nakano and  K.  Kurafuchi: IEEE Trans. Device Mater. Reliab. 16 (2016) 588–596.
• 17)   Y.  Kariya,  H.  Yamaguchi,  M.  Itako,  N.  Mizumura and  K.  Sasaki: J. Smart Processing 2 (2013) 160–165.
• 18)   P.  Gadaud,  V.  Caccuri,  D.  Bertheau,  J.  Carr and  X.  Milhet: Mater. Sci. Eng. A 669 (2016) 379–386.
• 19)   M.  Okazaki and  T.  Koizumi: J. Metall. Trans. A 14 (1983) 1641–1648.
• 20)   J.  Zhao,  Y.  Mutoh,  Y.  Miyashita and  L.  Wang: J. Eng. Fract. Mech. 70 (2003) 2187–2197.
• 21)   H.  Nose,  M.  Sakane,  M.  Yamashita and  K.  Shiokawa: Trans. Jpn. Soc. Mech. Eng. A 68 (2002) 88–95.
• 22)   M.  Taniguchi and  Y.  Kariya: Mater. Trans. 57 (2016) 853–859.
• 23)   S.  Yip: Nature 391 (1998) 532–533.
• 24)   J.W.  Hutchinson: J. Mech. Phys. Solids 16 (1968) 13–31.
• 25)   J.R.  Rice and  G.F.  Rosengren: J. Mech. Phys. Solids 16 (1968) 1–12.
• 26)   J.D.  Landis and  J.A.  Begley: ASTM Spec. Tech. Publ. 590 (1976) 128–148.
• 27)   K.  Ohji,  K.  Ogura and  S.  Kubo: Trans. Jpn. Soc. Mech. Eng. A 42 (1976) 350–358.
• 28)   K.M.  Nikbin,  G.A.  Webster and  C.E.  Turner: ASTM Spec. Tech. Publ. 601 (1976) 47–62.