Composition Effect of Kondo Behavior in Au–Al–Ce Quasicrystalline Approximants

Abstract

We have studied the magnetic and transport properties of Tsai-type quasicrystalline approximants, Au_xAl_84−xCe₁₆ and Au_yAl_86−yCe₁₄ by the measurements of magnetic susceptibility χ, specific heat C_p and electrical resistivity ρ. A Curie-Weiss behavior in χ for all compounds indicates the stable trivalent state of Ce ions in Au–Al–Ce. The effective magnetic moment increases with increasing the Au concentration whereas the Weiss temperature decreases. These behaviors suggest the Kondo effect in Au–Al–Ce suppresses with the increase of Au concentration. In C_p, all measured compounds show a broad peak due to the Kondo resonance at 0.8 K. In addition, C_p/T shows a peak below 0.6 K, which implies the existence of spin-glass transition. In all compounds, a pronounced −log T behavior due to Kondo effect are observed in ρ(T) below 10 K. Moreover, Au_yAl_86−yCe₁₄ approximants are the first example displaying a precursor of coherent Kondo state at low temperatures because a broad maximum is observed in ρ(T) at 1.3 K.

Fig. 4 Electrical resistivity of (a) Au_xAl_84−xCe₁₆ and (b) Au_yAl_86−yCe₁₄.

1. Introduction

Since the discovery of stable icosahedral quasicrystal (QC) and its approximants (AC) in binary Cd–R (R = rare earth elements) system,¹⁾ magnetic and physical properties of rare-earth based Tsai-type QC’s and AC’s have been studied intensively.²⁾ In Cd₆R 1/1 AC, the first report of long-range antiferromagnetic order in AC was done for R = Tb,³⁾ then antiferromagnetic state has been observed at low temperatures in R = Pr, Nd, Sm, Gd, Dy, Ho, Er and Tm.⁴⁾ The long-range antiferromagnetic transition has been also discovered in ternary Au–Al–R with R = Gd and Tb.⁵⁾ Especially for R = Tb, a study of neutron diffraction reveals a complex and rotational spin arrangement that should be originated by the geometrical frustration inherent in the icosahedral spin cluster.⁶⁾ A similar complex spin order is also reported for a canted ferromagnetic order of Au–Si–Tb AC.⁷⁾

In some Ce- and Yb-based compounds, on the other hand, characteristic magnetic behaviors such as Kondo effect, heavy fermion and valence fluctuation have been observed in addition to magnetic order.^8,9) Because the formation of heavy-fermion state results from strong correlation between 4f electrons and conduction electrons located near the Fermi energy, physics of strongly correlated electrons on the quasiperiodic structure where the Fermi energy is difficult to define has attracted some attention. In fact, a quantum critical behavior that is one of characteristic phenomena in the strongly correlated electron system was discovered in Au–Al–Yb QC.^10,11) Although a quantum critical behavior is manifested in Au–Al–Yb AC under hydrostatic pressure,¹²⁾ the quantum criticality of quasicrystalline phase shows a pronounced difference with that for approximants and other Ce and Yb compounds^13,14) in terms of robustness of critical state against pressure. In accordance with the observations of various magnetic features in Au–Al–R system, some unconventional magnetic properties should be expected to observed in other rare earth systems. In this paper, focusing on R = Ce which is vigorously studied in the heavy fermions, we report the magnetic and transport properties of Au–Al–Ce AC by the results of magnetic susceptibility, specific heat and electrical resistivity measurements. In Au–Al–Ce AC, cubic 1/1 and 2/1 approximants exist as observed in Au–Ga–Eu,¹⁵⁾ although no QC phases have been discovered yet. We used samples of Au_xAl_84−xCe₁₆ and Au₆₄Al₂₂Ce₁₄ for 2/1 approximants and Au₇₆Al₁₀Ce₁₄ for 1/1 ones in this study. Especially, for the first time in QC and AC, we observed a resistivity anomaly indicating a precursor for coherent Kondo state in Au_yAl_86−yCe₁₄ approximants.

2. Experimental Procedure

Polycrystalline samples of Au_xAl_84−xCe₁₆ (x = 62, 64, 66, 70) and Au_yAl_86−yCe₁₄ (y = 64 and 76) were prepared by arc-melting the constituent amount of pure Au, Al, Ce elements. The obtained ingots were then annealed at 1073 K for 50 h. Powder x-ray diffraction patterns of Au–Al–Ce are shown in Fig. 1(a). Bragg peaks at 40° < 2θ < 46° indicate that all Au_xAl_84−xCe₁₆ and Au₆₄Al₂₂Ce₁₄ crystallize in Tsai-type 2/1 cubic approximant and Au₇₆Al₁₀Ce₁₄ shows the 1/1 approximant. In Au_xAl_84−xCe₁₆, peaks of Au₅₁Ce₁₄ impurity phase are observed as indicated by cross marks in Fig. 1. On the other hand, no additional peaks due to a secondary phase are observed in Au_yAl_86−yCe₁₄. The estimated values of lattice parameters a for Au–Al–Ce are summarized in Table 1. Dependence of a on the concentration of Au for Au_xAl_84−xCe₁₆ is shown in Fig. 1(b). At Fig. 1(b), the relation a_2/1/a_1/1 ∼ τ, where τ is the golden ratio, is used for the comparison between Au₇₆Al₁₀Ce₁₄ and other 2/1 approximants.¹⁶⁾ Figure 1(b) reveals that the unit cell volume of Au_xAl_84−xCe₁₆ increases with increasing Au, which tendency agrees with that observed in Au–Al–Gd 1/1 approximants.¹⁷⁾

Fig. 1

(a) Powder x-ray diffraction patterns for Au–Al–Ce AC. Calculated patterns for Tsai-type 1/1 and 2/1 approximants are also shown. The cross marks represent the Bragg peaks of Au₅₁Ce₁₄ impurity. (b) Au concentration dependence of the lattice parameters for Au–Al–Ce AC. The value for Au₇₆Al₁₀Ce₁₄ 1/1 approximant is multiplied by the golden ratio τ.

Table 1 Cubic lattice parameter a, effective magnetic moment μ_eff and paramagnetic Curie temperature θ_p for Au–Al–Ce AC.

The magnetic susceptibility χ(T) was measured by using a commercial SQUID magnetometer (Quantum Design MPMS) in the temperature range from 300 K down to 2 K under the magnetic field μ₀H = 1 T. The measurements of electrical resistivity ρ(T) were performed by conventional four terminal method using a home-build ³He refrigerator. The specific heat C(T) was measured on a Quantum Design PPMS with He3 option in the temperature range from 20 K down to 0.5 K. In addition, the ADR option for PPMS was used for the ρ(T) and C(T) measurements down to 0.1 K.

3. Results and Discussions

3.1 Magnetic susceptibility

Figure 2(a) and (b) show the temperature dependence of inverse magnetic susceptibility χ⁻¹ for Au_xAl_84−xCe₁₆ and Au_yAl_86−yCe₁₄, respectively. Linear temperature dependencies of χ⁻¹ below 300 K indicate that all systems obey the Curie-Weiss law. The effective magnetic moment μ_eff and paramagnetic Curie temperature θ_p obtained by the least-square fitting above 50 K are summarized in Table 1. The obtained values of μ_eff are in the range from 2.4 μ_B to 2.5 μ_B, which are comparable to the free ion value of Ce³⁺ (2.54 μ_B). This result indicates the stable trivalency of Ce ions in Au–Al–Ce AC. As shown in Fig. 2(c), μ_eff increases with increasing the concentration of Au while θ_p decreases in Au_xAl_84−xCe₁₆, indicating that the Kondo effect in Au_xAl_84−xCe₁₆ suppresses with increasing the concentration of Au. This feature is consistent with the increase of unit-cell volume with increasing Au for Au–Al–R¹⁶⁾ because the strength of Kondo effect in most Ce compounds is suppressed by the volume expansion.¹³⁾ The μ_eff for Au_yAl_86−yCe₁₄ shows the same tendency as observed in Au_xAl_84−xCe₁₆, but the values of θ_p for Au_yAl_86−yCe₁₄ are nearly constant and smaller than the half of those for Au_xAl_84−xCe₁₆. The suppressed θ_p’s for Au_yAl_86−yCe₁₄ suggest that the Ce 4f electrons in Au_yAl_86−yCe₁₄ is more localized than those in Au_xAl_84−xCe₁₆ because of larger unit-cell volume as shown in Fig. 2(b).

Fig. 2

Inverse magnetic susceptibility of (a) Au_xAl_84−xCe₁₆ and (b) Au_yAl_86−yCe₁₄. Variations of effective magnetic moment μ_eff and paramagnetic Curie temperature θ_p with respect to Au concentration are shown in (c).

3.2 Specific heat

Figure 3(a) shows the specific heat C(T) for Au–Al–Ce AC’s below 10 K. All compounds show a maximum at 0.6 K. In Au₆₆Al₁₈Ce₁₆ and Au₇₆Al₁₀Ce₁₄, moreover, a shoulder-like anomaly is observed at 0.4 K and 0.25 K, respectively. These low-temperature anomalies in Au₆₆Al₁₈Ce₁₆ and Au₇₆Al₁₀Ce₁₄ are clearly visualized as a peak in C/T shown in Fig. 3(b). In addition, a peaking behavior is also seen at 0.5 K in C/T for Au₆₆Al₁₈Ce₁₆. A similar peak in C/T is observed in other Ce-based AC Ag–In–Ce.^18,19) These reports argue that the origin of C/T peak at 0.4 K in Ag–In–Ce is a spin-glass transition because a sharp cusp is observed in ac-susceptibility at the freezing temperature T_f = 0.3 K. Therefore, peaks in C/T for several Au–Al–Ce should also result from a spin-glass freezing.

Fig. 3

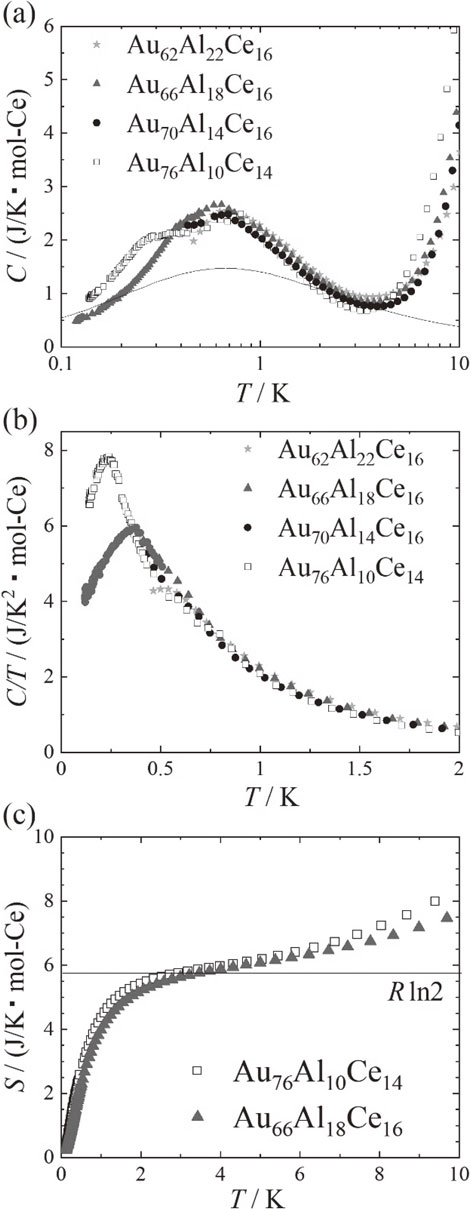
Temperature dependence of (a) specific heat C, (b) C/T, and (c) entropy for Au–Al–Ce AC. A solid line in (a) represents the estimated contribution of Kondo resonance, and a horizontal line in (c) indicates R ln 2.

On the other hand, the broad peak in C(T) for Au–Al–Ce should be originated by Ce 4f electrons because, as shown in Fig. 3(c), the entropy derived from the integration of C/T reaches R ln 2 at 4 K at which a minimum shows in C(T). As mentioned in the next section, resistivity for all Au–Al–Ce compounds shows a logarithmic increase due to Kondo effect. Thus we suggest that the peak at 0.6 K in C(T) is that predicted by the impurity Kondo model.⁹⁾ By using the calculated C for S = 1/2 Coqblin-Schrieffer model,²⁰⁾ the temperature at the peak is reproduced when the Kondo temperature T_K is estimated as 1 K as shown by a solid line in Fig. 3(a). However, the measured maximum value of the peak is twice as large as the calculated one. This discrepancy may be caused from the absence of the contributions of spin-glass transition and/or the crystal field effect of the Ce 4f electrons.

3.3 Electrical resistivity

Figure 4(a) and (b) show the results of electrical resistivity reduced by the value at 300 K, ρ/ρ(300), for Au_xAl_84−xCe₁₆ and Au_yAl_86−yCe₁₄, respectively. At around 100 K, all compounds show a broad peak or shoulder-like anomaly. Then, on cooling below 10 K at which ρ(T) shows a minimum, a −log T behavior is observed. These two features are observed typically in Ce-based Kondo compounds. Therefore, Au–Al–Ce AC systems are categorized as dense Kondo systems.

Fig. 4

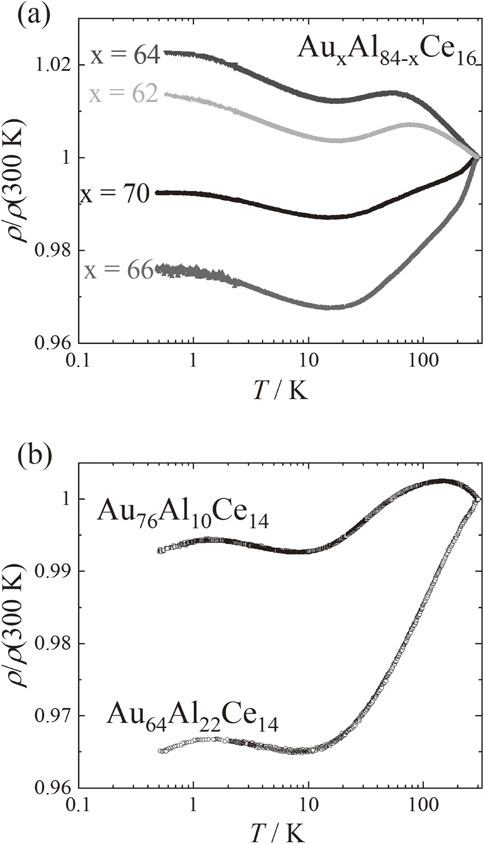
Electrical resistivity of (a) Au_xAl_84−xCe₁₆ and (b) Au_yAl_86−yCe₁₄.

For Au_xAl_84−xCe₁₆, ρ(T) shows a saturating behavior below 1 K that is conventional feature for the impurity Kondo systems, despite Au–Al–Ce AC possesses the periodicity. On the other hand, ρ(T)’s for both Au₇₆Al₁₀Ce₁₄ and Au₆₄Al₂₂Ce₁₄ display a pronounced maximum at 1.3 K. This behavior is the precursor to the coherent Kondo state that is characteristic for the heavy fermion systems⁹⁾ thereby Au_yAl_86−yCe₁₄ approximants should be the first example of coherent Kondo AC. Since the samples of Au_yAl_86−yCe₁₄ are nearly single phase whereas those of Au_xAl_84−xCe₁₆ contain small amount of Au₅₁Ce₁₄ impurity phase, the low-temperature coherent state in Au–Al–Ce AC should be sensitive to the sample quality. Thus it should be worth studying the magnetic property of Au–Al–Ce AC by using single crystals.

4. Summary

In summary, we performed measurements of magnetic susceptibility, specific heat and electrical resistivity for a series of Au–Al–Ce quasicrystalline approximants, Au_xAl_84−xCe₁₆ and Au_yAl_86−yCe₁₄. Curie-Weiss behavior in the magnetic susceptibility indicates the stable trivalency of Ce ions in all Au–Al–Ce approximants. The effect of composition on the effective magnetic moment and paramagnetic Curie temperature reveals that the strength of Kondo effect decreases with increasing the concentration of gold. Low-temperature specific heat displays anomalies possibly due to the Kondo effect and spin-glass freezing. The electrical resistivity of all Au–Al–Ce approximants shows a −log T behavior characteristic for Ce Kondo compounds below 10 K. Furthermore, we first observed a resistivity maximum at 1.3 K that is a precursor of coherent Kondo state in Au_yAl_86−yCe₁₄ approximants.

Acknowledgments

The authors thank S. Suzuki for fruitful discussion. This work was supported by JSPS KAKENHI Grant Number JP19H05818.

REFERENCES

• 1)   P.  Tsai,  J.Q.  Guo,  E.  Abe,  H.  Takakura and  T.J.  Sato: Nature 408 (2000) 537–538.
• 2)   A.I.  Goldman: Sci. Technol. Adv. Mater. 15 (2014) 044801.
• 3)   R.  Tamura,  Y.  Muro,  T.  Hiroto,  K.  Nishimoto and  T.  Takabatake: Phys. Rev. B 82 (2010) 220201(R).
• 4)   A.  Mori,  H.  Ota,  S.  Yoshiuchi,  K.  Iwakawa,  Y.  Taga,  Y.  Hirose,  T.  Takeuchi,  E.  Yamamoto,  Y.  Haga,  F.  Honda,  R.  Settai and  Y.  Ōnuki: J. Phys. Soc. Jpn. 81 (2012) 024720.
• 5)   A.  Ishikawa,  T.  Fujii,  T.  Takeuchi,  T.  Yamada,  Y.  Matsushita and  R.  Tamura: Phys. Rev. B 98 (2018) 220403(R).
• 6)   T.J.  Sato,  A.  Ishikawa,  A.  Sakurai,  M.  Hattori,  M.  Avdeev and  R.  Tamura: Phys. Rev. B 100 (2019) 054417.
• 7)   T.  Hiroto,  T.J.  Sato,  H.  Cao,  T.  Hawai,  T.  Yokoo,  S.  Itoh and  R.  Tamura: J. Phys. Cond. Mat. 32 (2020) 415802.
• 8)   G.R.  Stewart: Rev. Mod. Phys. 56 (1984) 755–787.
• 9)  A.C. Hewson: The Kondo Problem to Heavy Fermions, (Cambridge University Press, Cambridge, 1993).
• 10)   K.  Deguchi,  S.  Matsukawa,  N.K.  Sato,  T.  Hattori,  K.  Ishida,  H.  Takakura and  T.  Ishimasa: Nat. Mater. 11 (2012) 1013–1016.
• 11)   T.  Watanuki,  S.  Kashimoto,  D.  Kawana,  T.  Yamazaki,  A.  Machida,  Y.  Tanaka and  T.J.  Sato: Phys. Rev. B 86 (2012) 094201.
• 12)   S.  Matsukawa,  K.  Deguchi,  K.  Imura,  T.  Ishimasa and  N.K.  Sato: J. Phys. Soc. Jpn. 85 (2016) 063706.
• 13)   G.R.  Stewart: Rev. Mod. Phys. 73 (2001) 797–855.
• 14)   H.v.  Löhneysen,  A.  Rosch,  M.  Vojta and  P.  Wölfle: Rev. Mod. Phys. 79 (2007) 1015.
• 15)   S.  Yoshida,  S.  Suzuki,  T.  Yamada,  T.  Fujii,  A.  Ishikawa and  R.  Tamura: Phys. Rev. B 100 (2019) 180409(R).
• 16)   Y.G.  So,  K.  Takagi and  T.J.  Sato: J. Phys. Conf. Ser. 1458 (2020) 012003.
• 17)   A.  Ishikawa,  T.  Hiroto,  K.  Tokiwa,  T.  Fujii and  R.  Tamura: Phys. Rev. B 93 (2016) 024416.
• 18)   K.  Imura,  K.  Nobe,  K.  Deguchi,  M.  Matsumura,  H.  Miyazaki,  A.  Yasui,  E.  Ikenaga and  N.K.  Sato: J. Phys. Soc. Jpn. 86 (2017) 093702.
• 19)   T.  Sawano,  Y.  Shinagawa,  T.  Shiino,  K.  Imura,  K.  Deguchi and  N.K.  Sato: AIP Adv. 8 (2018) 101306.
• 20)   V.T.  Rajan: Phys. Rev. Lett. 51 (1983) 308–311.