2021 Volume 62 Issue 8 Pages 1168-1176
2021 Volume 62 Issue 8 Pages 1168-1176
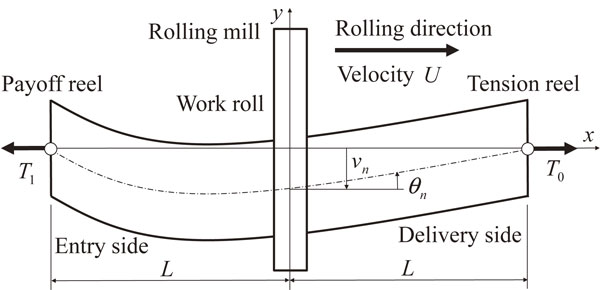
The temper rolling process of hot-rolled strips is the final rolling step to improve the flatness of the strips and shape slippage of the coiled strips. Poor flatness of a hot-rolled strip causes lateral movement of the strip during the temper rolling process. Manual leveling operations to control this movement result in a much lower line speed and productivity. Moreover, the quality of manual leveling is not consistent, as it depends on the operator’s experience. Lack of understanding of the lateral movement phenomenon has sustained manual operation and discouraged the development of an automatic control system. To solve this problem, the authors propose both a new lateral movement model and a theoretical method. A lateral movement model for temper rolling and a large-deflection strip model are important components in the new model. In the method, lateral movement stability is equivalent to an eigenvalue problem with lateral movement static equations. Their usefulness is confirmed by comparing the results of experimental rolling in the laboratory with those of numerical calculations. The simulation results obtained using the proposed models confirm that actual problems can be solved more exactly than with the conventional linear model. Thus, simulation using the proposed models can support the investigation of lateral movement problems and the development of an automatic control system.
This Paper was Originally Published in Japanese in J. Jpn. Soc. Technol. Plast. 61 (2020) 107–114. The captions of figures were slightly modified.
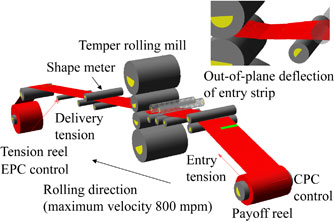
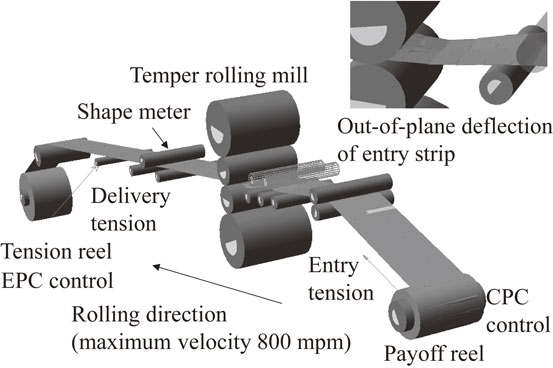
The temper rolling process of hot-rolled steel strips, which improves the flatness of the strips and shape slippage of the coiled strips, prevents lateral movement of hot-rolled strips in downstream process lines. Figure 1 shows a developed control system of a temper rolling line. The automatic control system provides elongation setup based on a shape prediction model,1) dynamic control of flatness and elongation2) and control of lateral movement. The shape prediction model predicts the strip shape at the mill entry side by using physical models and sensing data in the hot rolling process. Elongation setup outputs the tolerance range of elongation based on the predicted strip shape at the entry side. Dynamic control of flatness and elongation controls the strip flatness to zero within the tolerance range of elongation. In this development, a strip lateral movement simulator for the temper rolling line, as shown in Fig. 2, was also developed. This numerical simulator makes it possible to assess the performance of the logic and the robustness of lateral movement control, and also enables assessment of operational conditions such as a strip tension. Its background theories are described in detail in the following.
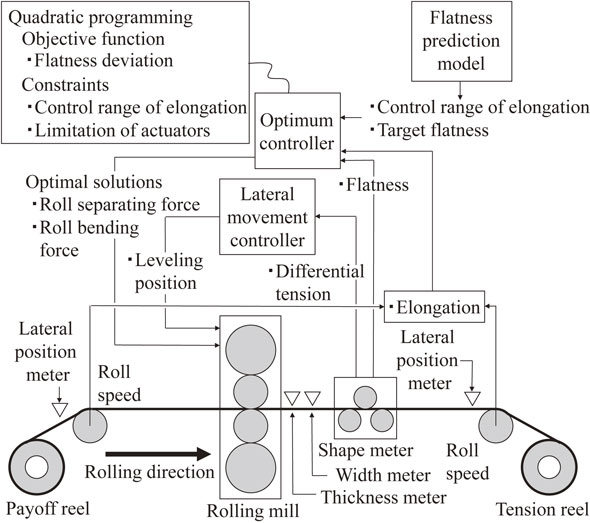
Dynamic control system of temper rolling line.
Strip lateral movement simulator for temper rolling line on ADAMS.
A strip sometimes appears to move in the lateral direction during rolling with a rolling mill.3) Because this lateral movement causes lower productivity and the work-roll damage, many researchers and engineers have studied and analyzed lateral movement in hot-strip4,5) and cold-strip3,6) rolling. A lateral movement analysis for strip rolling requires a coupled analysis of the strip lateral movement at the rolling mill and a model of strip deflection at the mill entry and delivery sides. In general, a beam model is used in the strip deflection model.3,6) The beam model is tuned to represent the actual results considering strip buckling. For example, bending stiffness is tuned to be smaller. On the other hand, from the viewpoints of calculation time and convergence, the coupled analysis7) of microscopic rolling phenomena and the standard elastic shell model is practically difficult.
A large-deflection strip model8) and a large-deflection discrete strip model9) have been developed to solve the above problems. The first model can be applied to a straight path and elastic bending and is formulated by approximating an elastic plate model. The second model can be applied to a curved path and elasto-plastic bending. The simulator shown in Fig. 2 represents the simulator based on the large-deflection discrete strip model. In the present study, a new lateral movement model (LMM) for temper rolling is derived from the approximation model for cold-strip rolling, considering the temper rolling reduction is very small. A LMM for a temper rolling line with payoff, rolling and coiling processes, is proposed, and its usefulness is confirmed by comparing the theoretical results, the results of experimental rolling in the laboratory and the results of numerical calculations. A lateral movement simulation of the simplex coiling process calculated by a general FEM has already been presented,10) but lateral movement simulation of a complex process such as a temper rolling line, including the payoff, rolling and coiling processes, is the first trial.
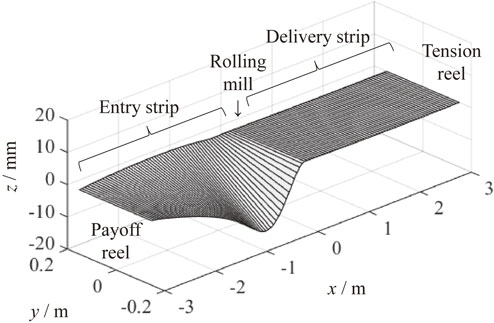
Figure 3 shows the experimental rolling line to clarify the proposed LMM. The line comprises a 2-high rolling mill, a payoff reel, a tension reel and deflector rolls at the entry and delivery sides. The LMM is solved by using either MATLAB/Simulink or MSC.ADAMS. The former has better compatibility with the large-deflection strip model,8) whereas the latter is a general analysis application for multi-body dynamics and has better compatibility with the large-deflection discrete strip model.9) The simulator in Fig. 2 was built on MSC.ADAMS. The modeling and calculation time of a simulator on MATLAB/Simulink is shorter. Each model on Simulink is represented as a block diagram. The block provides the model calculation and interface ports which input and output information such as forces and velocities. The block is represented by a state-space model and is described as a S-Function. The blocks represent the LMM at a payoff reel, referring to Appendix A2, the strip model at the entry side, the LMM of the temper mill, the strip model at the delivery side and the LMM at a tension reel with a boundary condition of simple support considering the deflector roll. These blocks are arranged in the order of strip movement. The unit system in this paper is the SI unit system.
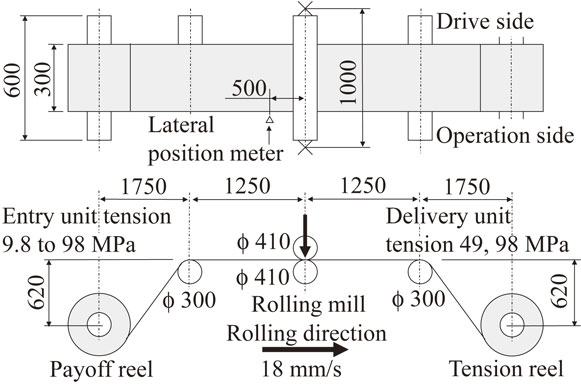
Experimental rolling line.
Figure 4 shows the schematic of strip lateral movement in temper rolling. The x-axis shows the strip rolling direction, and the y-axis shows the lateral direction. The LMM for cold rolling is formulated by using the Bland & Ford formula, which is an approximation of cold rolling. The LMM for temper rolling is formulated by simplifying the LMM for cold rolling, considering the very small reduction of the strip in temper rolling.
Schematic of strip lateral movement in temper rolling.
The work rolls of a rolling mill grip a strip. Assuming the strip velocity in the lateral direction is zero (non-slip), the constraint3,6) is given by
| \begin{equation} Dv_{n}/Dt = dv_{n}/dt + U\theta_{n} = 0 \end{equation} | (1) |
Considering the very small reduction in temper rolling and approximating the forward slip equation of Bland & Ford11) according to the formulation described in Appendix A1, the strip orientation angle velocity is given by
| \begin{equation} \frac{d\theta_{n}}{dt} = U\left\{- \frac{3}{4A}(h_{0df} - h_{1df}) + \frac{\beta_{M0}}{kI}M_{0} - \frac{\beta_{M1}}{kI}M_{1} - \kappa_{1} \right\} \end{equation} | (2) |
| \begin{equation*} \beta_{M0} = \frac{\sqrt{h/R'}}{4\mu \{1 - (T_{0} - 2\mu P_{0}^{e})/(kA)\}}\sqrt{r}, \end{equation*} |
| \begin{equation*} \beta_{M1} = \frac{\sqrt{h/R'}}{4\mu \{1 - (T_{1} - 2\mu P_{1}^{e})/(kA)\}}\sqrt{r} \end{equation*} |
Considering the plastic action on the rolled strip and the mill stiffness, the equation for the delivery wedge4) is given by
| \begin{align} h_{0df} & = \frac{1}{K_{l} + M_{l}}\biggl\{\frac{2bP}{b_{l}{}^{2}}v_{n} + \frac{bK_{l}}{b_{l}}S_{df} + M_{l}h_{1df}\\ &\quad - \frac{16bh_{r}K_{l}}{b_{r}{}^{2}}v_{n} + \frac{P}{khb_{l}{}^{2}(1 - \alpha_{c})}(M_{0} + M_{1})\biggr\} \end{align} | (3) |
| \begin{equation*} P = \left\{1.08 + r\left(1.79\mu \sqrt{\frac{R'}{h}} - 1.02 \right) \right\}k(1 - \alpha_{c})b\sqrt{R'hr}. \end{equation*} |
| \begin{equation*} M_{l} = \left\{0.54 + \frac{3r}{2}\left(1.79\mu \sqrt{\frac{R'}{h}} - 1.02 \right) \right\}\frac{k(1 - \alpha_{c})b^{3}}{6b_{l}{}^{2}}\sqrt{\frac{R'}{rh}}. \end{equation*} |
| \begin{equation*} \alpha_{c} = (T_{0} + T_{1} - 2\mu P_{0}^{e} - 2\mu P_{1}^{e})/(2kA). \end{equation*} |
Adding the camber curvature by rolling to the entry camber curvature κ1, the delivery camber curvature4) κ0 is given by
| \begin{equation} \kappa_{0} = (h_{0df} - h_{1df})/A + \kappa_{1}. \end{equation} | (4) |
The large-deflection strip model,8) which is an approximated model of the large-deflection plate model, is applied to simulations on MATLAB/Simulink as the strip deflection model. To shorten the calculation time, it is assumed that the strip model does not flow in the strip rolling direction within the analysis space (pseudo-Euler form). A FEM analysis of the plate model makes the process of camber flow difficult, and the many elements necessary in order to secure the convergence of a large-deflection FEM analysis result in a longer calculation time. On the other hand, using a basic beam model shortens the calculation time and improves the convergence of calculation, but the beam model prevents precise simulations. Therefore, we applied the large-deflection strip model, which is a specialized model for lateral movement problems and calculates out-of-plane elastic deflection with bending and twist, as shown in Fig. 5. The functional of the large-deflection strip model shown in Fig. 6 and the boundary conditions are given by
| \begin{align} \Pi & = \int_{0}^{L}\bigg\{\frac{EI}{2}(\cos \omega (\partial_{xx}v) + \sin \omega (\partial_{xx}w) - \kappa)^{2} \\ &\quad+ \frac{T}{2}(\partial_{x}v)^{2} \bigg\}dx\\ &\quad + \int_{0}^{L}\bigg\{\frac{Db}{2}(\sin \omega (\partial_{xx}v) - \cos \omega (\partial_{xx}w))^{2}\\ &\quad + \frac{T}{2}(\partial_{x}w)^{2} \bigg\}dx\\ &\quad + \int_{0}^{L}\bigg\{\frac{Db^{3}}{24}(\partial_{xx}\omega)^{2} + \left((1 - \nu)Db + \frac{Tb^{2}}{24} \right)(\partial_{x}\omega)^{2} \\ &\quad + \frac{Ehb^{5}}{1440}(\partial_{x}\omega)^{4} \bigg\}dx\\ &\quad + M_{z}^{E}(\partial_{x}v(t,0) - \theta_{E}) - M_{z}^{D}(\partial_{x}v(t,L) - \theta_{D})\\ &\quad - F_{y}^{E}(v(t,0) - v_{E}) + F_{y}^{D}(v(t,L) - v_{D}),\\ &\quad w(t,0) = w(t,L) = \partial_{x}w(t,0) = \partial_{x}w(t,L) = 0,\\ &\quad \omega (t,0) = \omega (t,L) = \partial_{x}\omega (t,0) = \partial_{x}\omega (t,L) = 0 \end{align} | (5) |
| \begin{equation*} D = Eh^{3}/12 \times (1 - \nu^{2})^{-1}. \end{equation*} |

Torsional strip with unstable lateral movement.
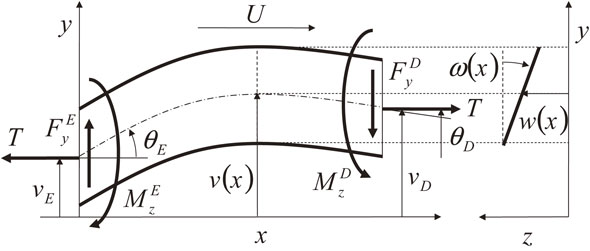
Large-deflection strip model.
The large-deflection strip model shown in Fig. 6 is calculated nonlinearly by using the Rayleigh-Ritz method.12) This calculation process is implemented by using a function of the MEX S-Function, where the calculation of the tangent stiffness matrix and a solver of the system of linear equations are programmed by using C/C++ language to shorten the calculation time.
The block diagram of the strip deflection model interacts with the block diagrams of the LMM at the mill or on the rolls through their information of forces and velocities. The advection equation of the camber curvature within a strip
| \begin{equation*} D\kappa/Dt = \partial_{t}\kappa + U\partial_{x}\kappa = 0 \end{equation*} |
The bifurcation point, where the path of lateral movement changes from convergence to divergence with a decrease of entry tension, is known.13) Here, the validity of the LMM of the temper rolling line is clarified by performing experimental rolling in the laboratory and comparing the experimental results of the bifurcation point with the theoretical results.
Table 1 shows the experimental rolling conditions. The underlined values are the values of the experimental conditions. First, steel strip rolling was stabilized without lateral movement in the initial state of the experiments. The entry and delivery unit tensions were set to be 49 MPa, and the lateral displacement at the mill in manual leveling was set so as to achieve a convergence of within 3 mm. Experimental rolling was started after the entry unit tension was set to 29 MPa, and the entry tension was then decreased stepwise during rolling while monitoring the strip lateral movement. Rolling was stopped when the lateral displacement at the mill exceeded a specified value. Figure 7 shows the results of this experiment, where the vertical axis shows the lateral displacement at the mill and the horizontal axis shows time. The path of the lateral displacement converged when the entry unit tension was above 20 MPa, and diverged when the entry unit tension was below 10 MPa. The elongation in this experiment was about 1.5%. Figure 8 shows the experimental results when the delivery unit tension was set to 98 MPa and the other experimental conditions were the same as those shown in Fig. 7. The path of the lateral displacement converged when the entry unit tension was above 20 MPa, and diverged when the entry unit tension was below 10 MPa. Lateral displacement seemed to increase gradually when the entry unit tension was 20 MPa. The elongation in this experiment was about 2.0%.
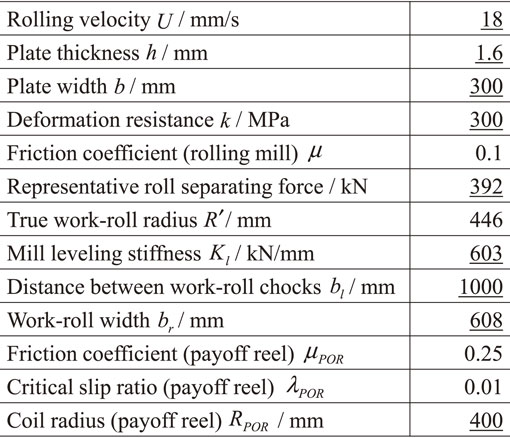
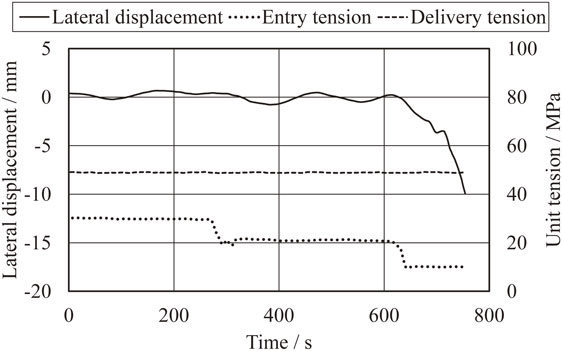
Experimental results (delivery unit tension 49 MPa).
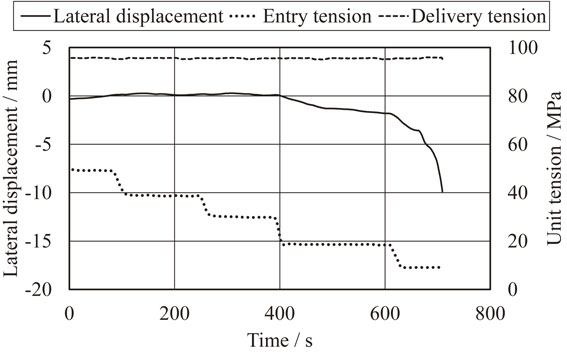
Experimental results (delivery unit tension 98 MPa).
These experiments confirmed that the critical entry tension, which is the smallest tension for maintaining stable lateral movement, existed at the bifurcation point. The critical entry tension slightly increased and lateral movement seemed to become slightly unstable when the delivery tension was larger. Hence, it is considered that the delivery tension did not seriously affect the phenomena of lateral movement in these experiments.
3.2 Clarification of LMM by eigenvalue analysis for steady state of lateral movementIn this section, the mechanism of the experimental phenomena is theoretically analyzed by using lateral movement equations. It is considered that lateral deflection converges if the steady state of lateral movement3) exists and diverges if it does not exist. Figure 4 shows the schematic of the analyzed lateral movement. The strips at the entry and delivery sides are assumed to be an elastic beam (restricted to in-plane bending) with the length of L. Considering the bias errors are zero, i.e.,
| \begin{equation*} h_{1df} = 0,\quad \kappa_{1} = 0,\quad S_{df} = 0 \end{equation*} |
| \begin{equation} \theta_{n} = \partial_{x}v_{0}(0) = 0, \end{equation} | (6) |
| \begin{equation} - \frac{3}{4}h_{0df} + \frac{12\beta_{M0}}{kb^{2}}M_{0} - \frac{12\beta_{M1}}{kb^{2}}M_{1} = 0 \end{equation} | (7) |
| \begin{equation} h_{0df} = \gamma v_{n} + \tau (M_{0} + M_{1}) \end{equation} | (8) |
| \begin{align*} \gamma &= \frac{2b}{K_{l} + M_{l}}\left(\frac{P}{b_{l}{}^{2}} - \frac{8h_{r}K_{l}}{b_{r}{}^{2}} \right), \\ \tau &= \frac{P}{khb_{l}{}^{2}(1 - \alpha_{c})(K_{l} + M_{l})}. \end{align*} |
| \begin{equation} - \gamma v_{n} - S_{0}M_{0} - S_{1}M_{1} = 0 \end{equation} | (9) |
| \begin{equation*} S_{0} = \tau - 16\beta_{M0}/(kb^{2}),\quad S_{1} = \tau + 16\beta_{M1}/(kb^{2}). \end{equation*} |
The lateral deflection equation of the entry beam is given by
| \begin{equation} EI\partial_{xxxx}v_{1} - T_{1}\partial_{xx}v_{1} = 0\quad (- L \leq x \leq 0) \end{equation} | (10) |
| \begin{equation} EI\partial_{xxxx}v_{0} - T_{0}\partial_{xx}v_{0} = 0\quad (0 \leq x \leq L). \end{equation} | (11) |
Considering the fact that the coiled strips on the payoff reel are rubbed together with a very small slip rate, the boundary conditions at the payoff reel are formulated as described in Appendix A2 and are represented by
| \begin{equation} v_{1}(- L) - S_{2}\partial_{x}v_{1}(- L) = 0, \end{equation} | (12) |
| \begin{align} &{- S}_{3}T_{1}\partial_{x}v_{1}(- L) - S_{2}EI\partial_{xxx}v_{1}(- L) \\ &\quad + EI\partial_{xx}v_{1}(- L) = 0 \end{align} | (13) |
| \begin{equation*} S_{2} = \phi_{\textit{POR}}R_{\textit{POR}},\quad S_{3} = \phi_{\textit{POR}}^{2}R_{\textit{POR}}\mu_{\textit{POR}}/(2\lambda_{\textit{POR}}), \end{equation*} |
The boundary conditions at the tension reel are represented by
| \begin{equation} v_{0}(L) = 0, \end{equation} | (14) |
| \begin{equation} EI(\partial_{xx}v_{0}(L) - \kappa_{0}) = 0. \end{equation} | (15) |
| \begin{equation} \kappa_{0} = \left(1 + \frac{\tau EI}{A} \right)^{-1}\left\{\frac{\gamma}{A}v_{0}(0) + \frac{\tau EI}{A}(\partial_{xx}v_{0}(0) + \partial_{xx}v_{1}(0)) \right\}. \end{equation} | (16) |
| \begin{align} &- \left(1 + \frac{\tau EI}{A} \right)\partial_{xx}v_{0}(L) + \frac{\gamma}{A}v_{0}(0) \\ &\quad+ \frac{\tau EI}{A}(\partial_{xx}v_{0}(0) + \partial_{xx}v_{1}(0)) = 0. \end{align} | (17) |
The connection conditions between the entry strip and the delivery strip at the mill are given by
| \begin{equation} v_{1}(0) - v_{0}(0) = 0,\quad \partial_{x}v_{1}(0) - \partial_{x}v_{0}(0) = 0. \end{equation} | (18) |
| \begin{equation} {- \gamma} v_{n} - S_{0}EI(\partial_{xx}v_{0}(0) - \kappa_{0}) - S_{1}EI\partial_{xx}v_{1}(0) = 0. \end{equation} | (19) |
| \begin{align} &EI\left\{S_{1} + (S_{1} - S_{0})\frac{\tau EI}{A} \right\}\partial_{xx}v_{1}(0) + S_{0}EI\partial_{xx}v_{0}(0) \\ &\quad + \gamma \left(1 - \frac{S_{0}EI}{A} + \frac{\tau EI}{A} \right)v_{0}(0) = 0. \end{align} | (20) |
Appling an eigenvalue analysis, where the eigenfunctions are the lateral deflection v1 and v0, to the linear system represented by the field equations of eqs. (10) and (11) and the boundary conditions of eqs. (6), (12), (13), (14), (17), (18) and (20) of the steady state, the condition if deflection solutions exist or not is formulated15) (eigenvalue problem). The general solutions of eqs. (10) and (11) are represented by
| \begin{align} v_{1}(x)& = C_{1} + C_{2}x + C_{3}\sinh (\sqrt{T_{1}/(EI)} x) \\ &\quad + C_{4}\cosh (\sqrt{T_{1}/(EI)} x), \end{align} | (21) |
| \begin{align} v_{0}(x)& = D_{1} + D_{2}x + D_{3}\sinh (\sqrt{T_{0}/(EI)} x) \\ &\quad + D_{4}\cosh (\sqrt{T_{0}/(EI)} x) \end{align} | (22) |
| \begin{equation} [J]^{T} [C_{1} \quad C_{2} \quad C_{3} \quad C_{4} \quad D_{1} \quad D_{2} \quad D_{3} \quad D_{4}] = 0. \end{equation} | (23) |
| \begin{equation} | J (T_{0},T_{1},S_{0},S_{1},\gamma,\tau) | = 0. \end{equation} | (24) |
Figure 9 shows the numerical solution of eq. (24) obtained by using the experimental conditions in Table 1. Based on the calculation results of a discrete rolling model, the center deflection hr of the work-roll barrel was set to be
| \begin{equation*} h_{r} = 9.92 \times 10^{-13}\ [\text{m/N}] \times P. \end{equation*} |
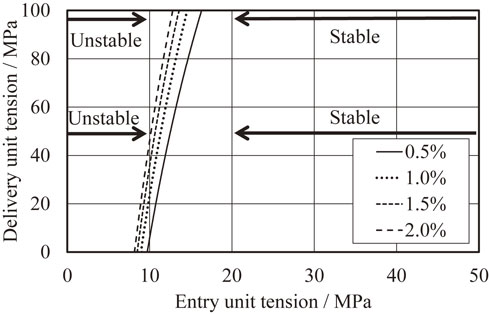
Phase diagram of strip lateral movement.
The lateral movement in experimental rolling is calculated by using the simulation built on MATLAB/Simulink. Figure 10 shows the simulation results of the lateral displacement at the mill in case of the delivery unit tension of 48 MPa. The horizontal axis and vertical axis show time and lateral displacement, respectively. A very small entry wedge of −0.45 µm was provided as the bias error so that the experimental results would agree with the simulation results. An entry unit tension of 22.05 MPa or more causes lateral movement to converge. On the other hand, the entry unit tension of under 17.15 MPa makes lateral movement diverge. Thus, the validity of the simulation is shown by the close agreement between the simulation results and the numerical results of eq. (24).
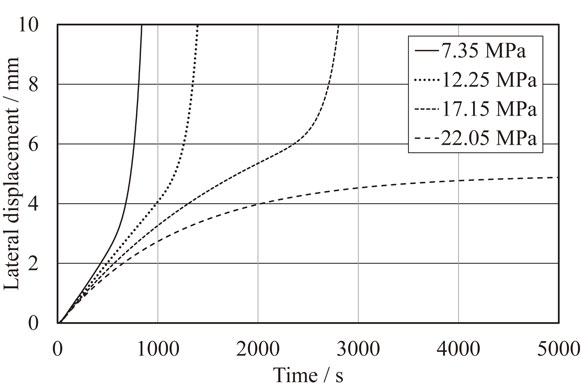
Simulation results of lateral displacement at rolling mill.
Figure 10 shows that the lateral displacement in case the entry unit tension of 7.35 MPa rapidly increases in about 700 s. Figure 11 shows the vertical deflections of the entry and delivery strips in 700 s. The z-axis shows the vertical direction. Out-of-plane deflection with torsion (lateral buckling) at the entry side of the mill, corresponding to Fig. 5, decreases the structural stiffness of a strip, and lower tension causes lateral buckling9) to occur more easily. On the other hand, the out-of-plane deflection at the delivery side of the mill in Fig. 11 does not appear, and also did not appear in the experiments.
Strip deflection.
Figure 12 shows the simulation results of the lateral deflection in case of the entry unit tension of 22.05 MPa shown in Fig. 10. The horizontal axis shows the position in the strip rolling direction, and the vertical axis shows lateral displacement. With progressing time, lateral deflection converges in the steady state governed by eqs. (6), (13) and (17) of the boundary conditions. Lateral displacement shows its maximum at the mill entry side in the initial state of the calculation. Its maximum point approaches the mill in the steady state governed by eq. (6). Figure 13 shows the simulation results of the lateral deflection for the entry unit tension of 7.35 MPa in Fig. 10. In this case, lateral deflection diverges with progressing time. The point initially approaches the mill and departs from the mill after 600 s. The point appears at the mill entry side when lateral deflection diverges and entry tension is smaller than delivery tension. From eq. (1), the strip orientation angle at the mill becomes negative and the lateral movement velocity becomes positive in this case. Therefore, lateral movement continues to increase, and finally, lateral buckling occurs in the entry strip after 600 s.
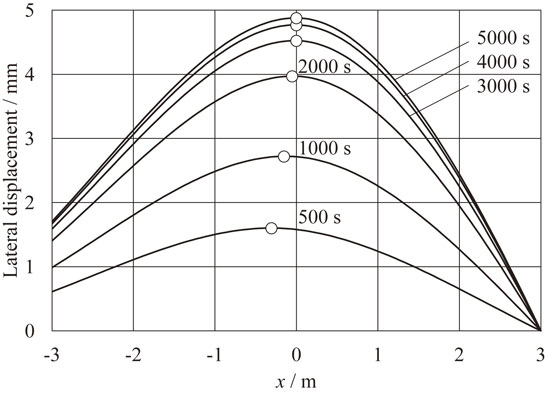
Simulation results of lateral deflection (entry unit tension 22.05 MPa).
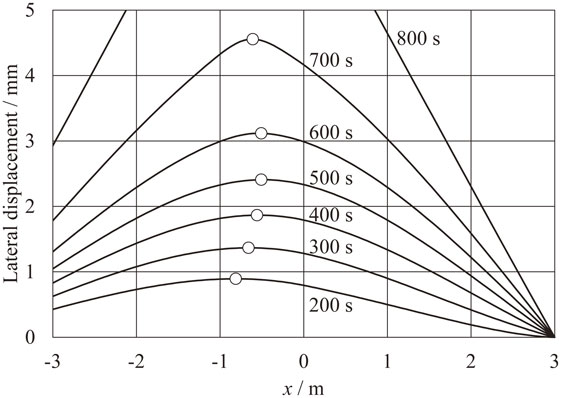
Simulation results of lateral deflection (entry unit tension 7.35 MPa).
The simulation results when the strip deflection model of the entry and delivery sides is a beam model constrained to in-plane deflection must agree with the discriminant of eq. (24). The broken curves in Fig. 14 show the simulation results of the lateral displacement at the mill when using a beam model. As in Fig. 10, the delivery tension is 49 MPa. The entry wedge, which is a bias error, is a relatively large value of −2.25 µm (that is, 5 times the value of −0.45 mm of the above-mentioned entry wedge, which is very small). The entry unit tensions of 9.8 MPa and 19.6 MPa cause lateral movement to diverge and converge, respectively. This linear dynamical system makes these results agree with the discriminant of eq. (24) regardless of the magnitude of bias errors.
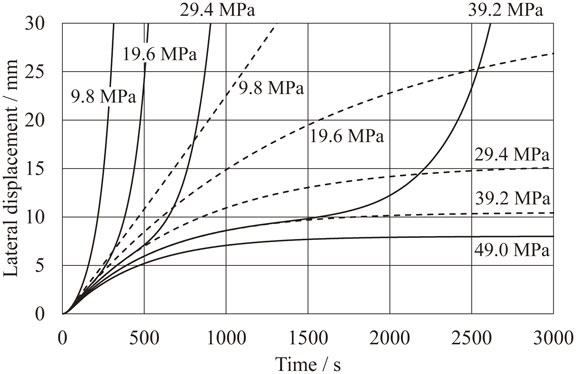
Simulation results of lateral displacement at rolling mill.
The solid curves in Fig. 14 show the simulation results of the lateral displacement at the mill when using the large-deflection strip model. The solid curves agree with the broken curves in the initial term of the calculations, but the solid curves in the case of smaller entry tension gradually depart from the broken curves with progressing time.
Figure 15 shows the phase diagram for the entry tension and the entry wedge based on the simulation results for reduction of 1.5%. The horizontal axis and vertical axis show the entry unit tension and the magnitude of the entry wedge, respectively. The solid curve and the broken line show the results obtained by using the large-deflection strip model and a beam model, respectively. The critical entry unit tension of 41.1 MPa obtained by using the large-deflection strip model is very different from the discriminant of eq. (24). Large values of the orientation angle θn or lateral displacement vn cause the lateral buckling in the entry strip to decrease the structural stiffness of the entry strip. Asymmetry error factors such as the entry wedge cause lateral movement. As mentioned above, this type of error cannot be ignored even if good operation is maintained in an actual temper rolling line. Applying the large-deflection strip model makes it possible to simulate lateral movement more safely. On the other hand, the discriminant of eq. (24) shows that asymmetry errors do not cause lateral movement, but the cause of lateral movement is an unstable dynamical system. Both a stable dynamical system and very small error make lateral movement converge. Facilities and operation must be managed in a stable condition for a dynamical system for lateral movement. It is considered that methods such as the discriminant of eq. (24) are valid as tools for a first-step study because these methods enable very simple calculation.
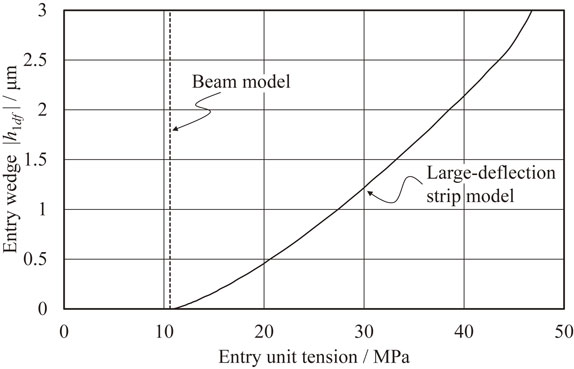
Phase diagram based on simulation results.
In this paper, the validity of lateral movement simulation was clarified by experimental rolling in the laboratory and a theoretical analysis with the aim of developing an automatic control system for the temper rolling line. The results obtained in this study are shown below.
It is considered that the proposed methods can be applied generally to lateral movement analysis problems other than the temper rolling line and are useful for investigating lateral movement problems in further detail. However, the proposed strip deflection model is designed specifically for strips with camber and cannot be applied to strips with various defective shapes. Therefore, it will be necessary to design a more practical strip deflection model for these strips.
The strip rotational velocity ψ0 at the mill delivery side is defined as
| \begin{equation} \psi_{0} = - \partial_{y}U \end{equation} | (A1-1) |
| \begin{align} \psi_{0}/U & = - (1 + f_{s})^{-1}\partial_{y}f_{s}\\ & = \beta_{h0}\frac{h_{0df}}{A} - \beta_{h1}\frac{(1 - r)h_{1df}}{A} + \beta_{M0}\frac{M_{0}}{kI} \\ &\quad - \beta_{M1}\frac{(1 - r)M_{1}}{kI} \end{align} | (A1-2) |
| \begin{equation} \beta_{h0} = - h(1 + f_{s})^{-1}\partial_{h}f_{s}, \end{equation} | (A1-3) |
| \begin{equation*} \beta_{h1} = h(1 - r)^{-1}(1 + f_{s})^{-1}\partial_{h1}f_{s}, \end{equation*} |
| \begin{equation} \beta_{M0} = k(1 + f_{s})^{-1}\partial_{\sigma 0}f_{s}, \end{equation} | (A1-4) |
| \begin{equation*} \beta_{M1} = - k(1 + f_{s})^{-1}\partial_{\sigma 1}f_{s}, \end{equation*} |
| \begin{align} \frac{\psi_{1}}{(1 - r)U} & = - (1 - \beta_{h0})\frac{h_{0df}}{A} + (1 - \beta_{h1})\frac{(1 - r)h_{1df}}{A}\\ &\quad + \beta_{M0}\frac{M_{0}}{kI} - \beta_{M1}\frac{(1 - r)M_{1}}{kI}. \end{align} | (A1-5) |
The entry rotational velocity ψ1 is also represented by3,6)
| \begin{equation} D\theta_{n}/Dt = d\theta_{n}/dt + (1 - r)U\kappa_{1} = \psi_{1} \end{equation} | (A1-6) |
| \begin{align} \frac{d\theta_{n}}{dt} &= U\bigg\{- (1 - \beta_{h0})\frac{h_{0df}}{A} + (1 - \beta_{h1})\frac{h_{1df}}{A} \\ &\quad + \beta_{M0}\frac{M_{0}}{kI} - \beta_{M1}\frac{M_{1}}{kI} - \kappa_{1} \bigg\}. \end{align} | (A1-7) |
Substituting Bland & Ford’s forward-slip equation11) in eq. (A1-3), the influence coefficient βh0 is represented by
| \begin{align} \beta_{h0} & =\Bigg( \frac{1}{2\sqrt{(1 - r)^{-1} - 1}} - \frac{\sqrt{\xi}}{2\mu}\\ &\quad + \frac{\sqrt{\xi}}{4\mu}\log \left(\frac{1}{1 - r}\left(\frac{k - \sigma_{0}}{k - \sigma_{1}} \right) \right) \Bigg)\\ &\quad \times \tan \bigg(\frac{1}{2}\mathop{\mathrm{atan}}\Big(\sqrt{(1 - r)^{-1} - 1}\Big) \\ &\quad - \frac{\sqrt{\xi}}{4\mu}\log \left(\frac{1}{1 - r}\left(\frac{k - \sigma_{0}}{k - \sigma_{1}} \right) \right) \bigg) \end{align} | (A1-8) |
Substituting Bland & Ford’s forward-slip equation11) in eq. (A1-4), the influence coefficient βM0 is represented by
| \begin{equation} \beta_{M0} = \frac{k\sqrt{\xi}}{2\mu (k - \sigma_{0})}\tan \left(\frac{1}{2}\mathop{\mathrm{atan}}(\sqrt{r}) - \frac{\sqrt{\xi}}{4\mu}\log (r + 1) \right). \end{equation} | (A1-9) |
| \begin{equation} \beta_{M0} = \frac{k\sqrt{\xi}}{4\mu (k - \sigma_{0})}\sqrt{r} + o^{2}(\sqrt{r}). \end{equation} | (A1-10) |
Figure A2-1 shows the force and moment acting on a strip that winds around a coil at a payoff reel. It is considered that the winding strip is developed to become a rigid body, and this rigid body moves on the developed plane of the coil. The surface of the rigid body moves from the left side to the right side. The entry endpoint (left endpoint) of the rigid body is fixed against the lateral direction, and the delivery endpoint (right endpoint) is connected with an elastic beam. The lateral friction force $F_{\textit{POR}}^{f}$
| \begin{equation} F_{\textit{POR}}^{f} = - \frac{\phi_{\textit{POR}}\mu_{\textit{POR}}T_{1}}{\lambda_{\textit{POR}}U}\left(\frac{dv_{\textit{POR}}}{dt} + U\theta_{\textit{POR}} \right) \end{equation} | (A2-1) |
| \begin{equation} M_{\textit{POR}}^{f} = - \frac{\phi_{\textit{POR}}\mu_{\textit{POR}}T_{1}}{12\lambda_{\textit{POR}}U}(\phi_{\textit{POR}}^{2}R_{\textit{POR}}^{2} + b^{2})\frac{d\theta_{\textit{POR}}}{dt} \end{equation} | (A2-2) |
| \begin{equation} v_{\textit{POR}} = \phi_{\textit{POR}}R_{\textit{POR}}\theta_{\textit{POR}}. \end{equation} | (A2-3) |
| \begin{align} &\phi_{\textit{POR}}R_{\textit{POR}}F_{\textit{POR}}^{f}/2 + M_{\textit{POR}}^{f} + \phi_{\textit{POR}}R_{\textit{POR}}F_{\textit{POR}}^{D}\\ &\quad - T_{1}v_{\textit{POR}} + M_{\textit{POR}} = 0 \end{align} | (A2-4) |
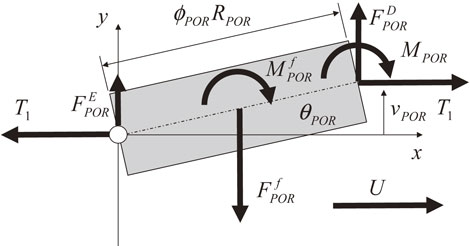
Rigid body on coil.
Lateral force $F_{\textit{POR}}^{D}$ is represented by
| \begin{equation} F_{\textit{POR}}^{D} = - (EI\partial_{xxx}v_{1}(- L) - T_{1}\partial_{x}v_{1}(- L)) \end{equation} | (A2-5) |
| \begin{equation} \theta_{\textit{POP}} = \partial_{x}v_{1}(- L),\quad v_{\textit{POR}} = v_{1}(- L). \end{equation} | (A2-6) |