生体分子系のための定量的粗視化分子力場の開発

概要

粗視化分子シミュレーションは，全原子シミュレーションでは到達できない時間および空間スケールの現象を解析するために有用なツールである．本稿では，生体分子系を対象に開発した粗視化分子力場について紹介する．粗視化分子力場の開発では，参照データとして全原子シミュレーションから取得したデータと実験データの両方を使用し，ボトムアップとトップダウンを組み合わせたアプローチを用いていた．完成した粗視化分子力場では，アミノ酸の膜透過自由エネルギーや膜表在タンパク質のアンカリング，膜貫通タンパクの二量化自由エネルギーなどの全原子シミュレーションによる計算値や実験値をよく再現することを確認し，膜タンパク系について定量的な解析が可能な粗視化分子力場の構築に成功した．

1　 はじめに

マクロ分子やその集合体を取り扱う生体分子系の分子動力学（MD）シミュレーションにおいて，粗視化（CG）分子力場は全原子モデルで到達できない空間および時間スケールのシミュレーションを達成可能にするための強力なツールである．定量的CG 力場であるSPICA［1,2］は，実験の密度や表面張力，溶媒和自由エネルギーなどの熱力学量や全原子（AA）MDから得られる分布関数をよく再現し，現象論を脱却した分子自己集合系の構造予測や熱力学的考察を可能とする．近年バージョンアップしたSPICA力場のタンパク質モデル［3］では，主鎖を代表する相互作用サイトにタンパク質の二次構造依存のパラメータを導入することでIntrinsically Disordered Protein（IDP）の慣性半径やタンパク質の脂質膜に対する吸着挙動を精度良く計算可能となった．しかしながら，SPICA力場のCG水モデルは無電荷であるため，脂質膜のような誘電率の空間変調が大きな系で静電相互作用を正しく記述することができない．

そこで，我々はSPICA力場へ極性を持つ水モデルを導入したpSPICA［4］力場をタンパク質系へ拡張することで，より広い生体分子系に関して静電相互作用の遮蔽効果を考慮したCG-MDを実行可能にした［5］．本稿では，そのタンパク質の粗視化分子力場開発プロセスにおける結果の一部と開発した力場を用いた粗視化分子シミュレーションの適用例について紹介する．

2　 タンパク質の粗視化分子モデリング

2.1　 モデル概要

まずpSPICAのタンパク質モデルについて概説する．pSPICAのCGモデリングスキームは基本的にSPICAのものを踏襲しており，タンパク質のCGユニットの定義はSPICAと同じである（図1）．タンパク質の主鎖（BB）は一つのCGユニットで代表され，側鎖（SC）は0–4個のCGユニットで構成される．ここで開発するタンパク質モデルはpSPICAの脂質モデルおよび水モデルと互換性があり，pSPICAの水モデルは粗視化モデルであるが極性を示すように三つの水分子を二つの互いに反対の電荷を持つCGユニットで表現している．この水モデルや脂質モデルの詳細については，論文［5］を参照されたい．

図1  タンパク質モデルの粗視化マッピング．

この粗視化力場における静電相互作用は，標準的なクーロンポテンシャルを用いて記述されるが，水と脂質膜の物性の実験値やAAモデルを用いた計算値を再現するため，比誘電率には3.2の値が設定されている．LJ相互作用については，以下の3種類の関数（LJ12−5, LJ12−4, LJ9−6）を使い分ける：

  

$$U_{\mathrm{LJ}}\left(r_{ij}\right)=\{\begin{array}{c}\hfill \frac{12}{7}{\left(\frac{12}{5}\right)}^{\frac{5}{7}}{\epsilon }_{ij}[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^5]\\ \hfill \frac{3\sqrt{3}}{2}{\epsilon }_{ij}[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^4]\\ \hfill \frac{27}{4}{\epsilon }_{ij}[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^9-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6]\end{array}$$(1)

ここで，ε_ijとσ_ijはU_LJ(σ_ij) = 0とmin{U_LJ(r_ij)} = −ε_ijを満たすLJパラメータである．LJ12−5は水とイオンの粗視化モデル間に適用され，電荷を持たないCGユニットと水間の相互作用にはLJ12−4が適用される．それ以外のLJ相互作用にはLJ9−6を用いる．

粗視化ユニット間の結合相互作用（Bond, Angle, Dihedral）については，以下の式で表現する：

  

$$U_{\mathrm{bond}}\left(r\right)=k_{\mathrm{bond}}{(r-r_0)}^2$$(2)

  

$$U_{\mathrm{angle}}\left(\theta \right)=k_{\mathrm{angle}}{(\theta -{\theta }_0)}^2$$(3)

  

$$U_{\mathrm{dihedral}}\left(\varphi \right)=k_{\mathrm{dihedral}}[1+cos(\varphi -d)]$$(4)

ここでk_{bond/angle/dihedral}は力の定数であり，r₀，θ₀，dはそれぞれ平衡長，平衡角，位相である．二面角ポテンシャルは環状SC（PHEおよびTYR）の平面性を保つために使用している．なお，タンパク質の二次構造は，調和ポテンシャルで記述される弾性ネットワークモデル（ENM）により維持し，カットオフ距離内にあるBBユニット間に適用する．

pSPICAにおけるCGタンパク質モデルの結合相互作用のパラメータはSPICAと同様にし，LJ相互作用のパラメータは表1に示した手順に従い実験値やAA計算から得られた結果を参照データとして最適化を行った．

表1 粗視化モデリングのパラメータ調整手順

Order	Target properties	pair
I	interfacial tension at SC analogue/water interface	Uncharged SC−water
II	hydration free energy of SC analogue	Uncharged SC−water
III	density of SC analogue solution	Charged SC−water
IV	radial distribution function of SC analogue dimers in water	Charged SC−SC
V	free energy of SC analogue across the lipid membrane	SC−lipid
VI	penetration depths and tilt angles of peripheral peptides/proteins	BB−lipid/water
VII	dimerization free energy of transmembrane helices	BB−BB/SC

2.2　 シミュレーション設定

CG-MDのシミュレーションソフトにはオープンソフトウェアのLAMMPS［6］を用いた．SPICAやpSPICAで適用されるポテンシャル関数を有するCG-SPICAパッケージが公式版LAMMPSに実装されているため，テーブル関数を使用することなくシミュレーションを実行できる．計算系は，PDBデータバンクの結晶構造データ［7］やCHARMM-GUI membrane builder［8］を使用することで全原子レベルでの構造を作成後，研究室で開発しているSPICAを用いたCG-MDセットアップスクリプトspica-tools［9］を使用して粗視化レベルの構造を用意した．AA-MDのシミュレーションソフトにはNAMD［10］を使用し，タンパク質と脂質の力場にはCHARMM36［11］を用いた．

3　 計算結果

3.1　 パラメータ調整計算

この節では，表1の粗視化モデリング手順の内，自由エネルギー計算を要したstep Vとstep VIIの結果について紹介する．

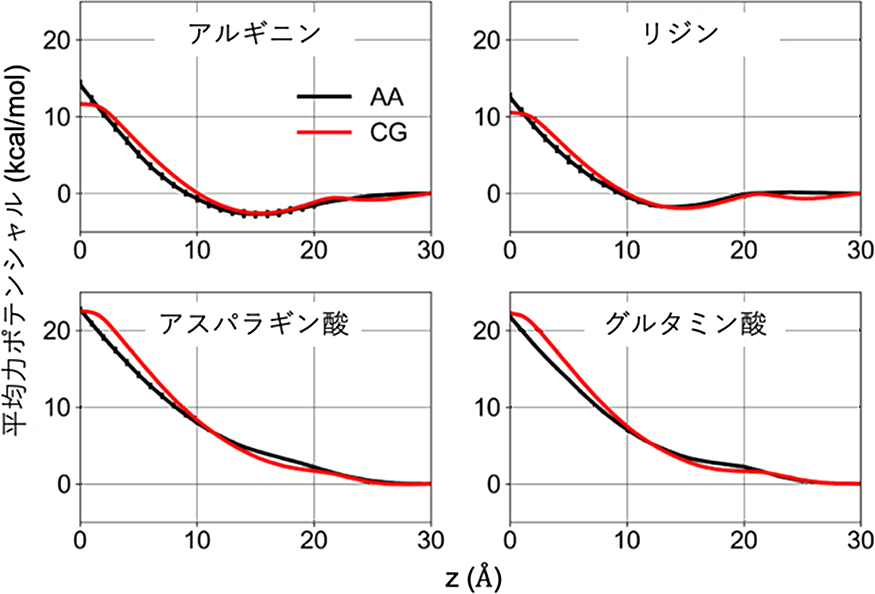
Step VではSCの膜透過自由エネルギーを計算しており，パルミトイルオレイルホスファチジルコリン（POPC）で構成される脂質二重層の中心とSC 1分子の間の膜垂直方向距離に沿って計算した．自由エネルギー計算にはAdaptive biasing force（ABF）法［12］を用い，CG-MDでは合計600 ns，AA-MDでは合計1200 nsのプロダクションランを実施することで自由エネルギープロファイルを算出した．得られた結果の内荷電SCに関するプロットを図2に示す．CG-MDの結果は，AA-MDの結果とよく一致していることがわかる．また，膜の中心部に荷電SCが挿入された状態を確認するとwater stringが形成されて膜の変形が起こっていた（図3）．これに由来する膜中心部における自由エネルギーの上昇は，非極性CG水モデルを採用しているSPICAでは自然に再現することができない．CG水モデルに極性を持たせたpSPICAではこのエネルギー上昇を捉えることが可能になった．後に示すように，このwater stringの安定性はタンパク質やペプチドが脂質膜に形成するチャネルの構造安定性に重要な要素となる．

図2  荷電SCの膜垂直方向に沿った膜透過自由エネルギープロファイル．

図3  膜中心付近に挿入されたリジンSCのスナップショット．緑と白は脂質頭部のコリンとリン酸，茶色は脂質尾部，水色の領域は水相を表す．

Step VIIでは膜貫通タンパク質の二量体化自由エネルギーの計算を実施した．自由エネルギー計算にはStep Vと同じくABF法を用いており，膜平行方向の二次元距離を反応座標とした平均力ポテンシャル（PMF）を算出した後，以下の式を使用することで二量体化自由エネルギーΔG_dimerを算出した：

  

$$K_a=\pi {\int }_0^{r_{max}}rexp\left[-\beta w\left(r\right)\right]dr$$(5)

  

$$\Delta G_{\mathrm{dimer}}=-RTln\left(K_a\right)$$(6)

ここでK_a，r_max，β，w(r)，R，Tは，それぞれ会合定数，積分におけるカットオフ距離，PMF，気体定数，計算系の温度である．計算には二量体化自由エネルギーの実験値が既知である5種類の膜貫通ペプチド，WALP，GpA，SerZipper，EphA1，ErbB1を用い，それぞれ合計3000 nsのCG-MDからPMFを算出した．得られた計算結果を表2に示す．二量体化自由エネルギーの計算値は全体的に実験値をよく再現しており，pSPICAを用いたCG-MDではタンパク質やペプチドの会合に関して適切な予測が可能であると期待できる．このような実験値やAA-MDの計算値を参照するトップダウンとボトムアップを組み合わせたモデリングを実施することで粗視化分子モデルのパラメータを調整し，脂質−タンパク質系のための定量的粗視化分子モデルの作成に成功した．

表2 膜貫通ペプチドの二量体化自由エネルギー（kcal/mol）［5］

Peptide	pSPICA	Exp.
WALP	−3.2±0.4	−2.2 to −6.2
GpA	−5.2±0.1	−3.2 to −7.5
SerZip	−7.1±1.2	<−8
EphA1	−2.1±0.2	−3.7±0.1
ErbB1	−2.6±0.5	−2.5±0.1

3.2　 応用計算

CGタンパク質モデルの完成後，モデルの性能を検証するために脂質−タンパク質系についてCG-MDを実施した．

まず，抗菌ペプチド（AMP）によって脂質膜に形成される細孔状態についてpSPICAを用いたCG-MDを実施した．AMPによって誘起される膜細孔は水チャネルであるため，その安定性は使用するタンパク質モデルだけでなく水モデルにも大きく依存する．ここでは，代表的な抗菌ペプチドであるmelittinによって形成された膜細孔のCG-MDを実施し，その安定性を確認した．初期配置はAA-MDを用いた先行研究［13］で得られたmelittin 6分子によりPOPC膜に細孔が形成された状態の構造をCGマッピングすることで作成した．異なる初期速度で開始した三つのレプリカについてpSPICAとSPICAを用いたCG-MDを実行し，得られた1 μs後の最終構造を図4に示す．またmelittinによって形成された細孔内に存在するCG水粒子数の時間変化を図5に示す．pSPICAを用いた計算では，melittinによって形成された細孔は，1 μs CG-MDの間，閉じることなく水チャネルを維持していた．一方，SPICAを用いた場合では，計算の途中で水チャネルが完全に閉じられたが，melittinは膜貫通状態となっていた．pSPICAとSPICAでは同じCGモデリングスキームを用いているが，CG水モデルの違いにより水チャネルの安定性が大きく異なることが実証された．またpSPICAを用いたCG-MDにおける膜細孔の半径は，細孔中心からの横方向の距離に沿った脂質尾部の数密度を計算することにより推定すると約1.8 nmで，以前のAA-MDの値である2.2 nmとかなり近い値となっていた．pSPICAでは，このような親水性の膜細孔を取り扱う計算系でAA-MDに匹敵する精度で構造予測が可能であることが期待できる．

図4  1 μs CG-MD後の最終構造．赤と緑はCG水粒子と脂質頭部のコリン，灰色は脂質尾部，茶色はmelittinを表す．

図5  melittinにより形成された膜細孔内のCG水粒子数の時間変化．

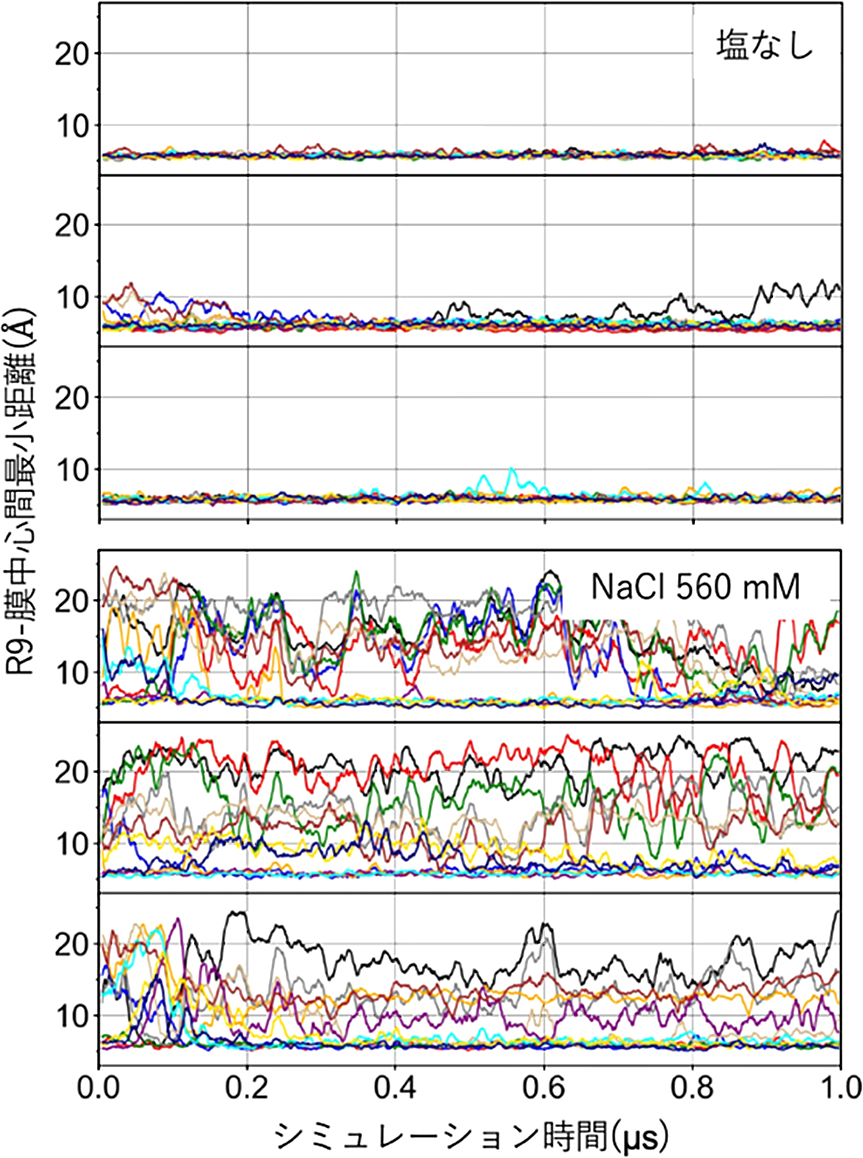
pSPICAとSPICAのCGモデリングスキームは膜表在ペプチドと膜貫通ペプチドをターゲットとしており，ペプチドの膜表面への吸着については再現すべき現象として考慮していなかった．そこで，AA-MDでも先行研究のあるノナアルギニン（R9）についてPOPC膜への吸着状態とその塩濃度依存性について検証を行った．12分子のR9を水中にランダムに配置し，塩濃度が異なる二つの系（塩なしと560 mM NaCl）についてpSPICAを用いたCG-MDを3回ずつ行い，計算中のR9と膜間の膜垂直方向最小距離を追跡した．シミュレーションを観察すると，R9は凝集体を形成しており，560 mM NaCl溶液での凝集体のサイズは塩なしの場合よりも大きいことがわかった．塩を含まない系ではR9間の静電反発によりその凝集が抑制されたが，560 mM NaClを含む系では塩のスクリーニング効果によってその静電反発が弱められたためだと考えられ，これらの結果はAA-MDや実験的研究の結果と一致していた［14］．図6に示すR9-膜間最小距離の時間変化を見ると，塩を含まない系では全てのR9がCG-MD開始直後に膜表面に吸着（最小距離5 Å）したが，560 mM NaClを含む系ではいくつかのR9が可逆的な膜吸着を示した．このR9の膜表面への吸着能の高さや塩濃度による膜吸着挙動の変化は，AA-MDでも観察されていた［15］．これらの結果から，pSPICAはペプチドの膜吸着過程についても有用であることが示された．

図6  melittinにより形成された膜細孔内のCG水粒子数の時間変化．

4　 まとめ

我々は極性CG水モデルをベースとした定量的CG力場pSPICAを拡張し，脂質／ペプチド／タンパク質に関する生体分子系のCG-MDを実現した．CGモデリングでは，実験値やAA-MDから得られた計算値を参照データとしたトップダウンとボトムアップを組み合わせたアプローチを採用しパラメータ調整を行うことで，定量的CGモデルの作成に成功した．モデル検証の計算では非極性CG水モデルをベースとするSPICAと比較を行うことで，水チャネルの形成を伴う計算におけるCG水モデルの重要性を示した．なお，pSPICAを用いたmelittin−POPC膜系の細孔形成過程に関するCG-MDは別の論文で報告されている［16］．また，CGモデリングのターゲットではなかったペプチドの膜表面への吸着についても，R9に関するCG-MDの結果が実験およびAA-MDの観測と一致していることを確認した．

 謝辞

本研究の実施にあたり，ご指導いただきました岡山大学篠田渉教授に感謝いたします．

参考文献

• [1]   S.  Seo and  W.  Shinoda, J. Chem. Theory Comput., 15, 762–774 (2019).
• [2]   S.  Kawamoto,  H.  Liu,  Y.  Miyazaki,  S.  Seo,  M.  Dixit,  R.  DeVane,  C.  MacDermaid,  G.  Fiorin,  M. L.  Klein and  W.  Shinoda, J. Chem. Theory Comput., 18, 3204–3217 (2022).
• [3]   T.  Yamada,  Y.  Miyazaki,  S.  Harada,  A.  Kumar,  S.  Vanni and  W.  Shinoda, J. Chem. Theory Comput., 19, 8967–8977 (2023).
• [4]   Y.  Miyazaki,  S.  Okazaki and  W.  Shinoda, J. Chem. Theory Comput., 16, 782–793 (2020).
• [5]   Y.  Miyazaki and  W.  Shinoda, J. Chem. Info. Model., 64, 532–542 (2024).
• [6]   A. P.  Thompson,  H. M.  Aktulga,  R.  Berger,  D. S.  Bolintineanu,  W. M.  Brown,  P. S.  Crozier,  P. J.  in ’t Veld,  A.  Kohlmeyer,  S. G.  Moore,  T. D.  Nguyen,  R.  Shan,  M. J.  Stevens,  J.  Tranchida,  C.  Trott and  S. J.  Plimpton, Comput. Phys. Commun., 271, 108171 (2022).
• [7]  https://www.rcsb.org/
• [8]   E. L.  Wu,  X.  Cheng,  S.  Jo,  H.  Rui,  K. C.  Song,  E. M.  Dávila-Contreras,  Y.  Qi,  J.  Lee,  V.  Monje-Galvan,  R. M.  Venable,  J. B.  Klauda and  W.  Im, J. Comput. Chem., 35, 1997–2004 (2014).
• [9]  https://github.com/SPICA-group/spica-tools
• [10]   J. C.  Phillips,  R.  Braun,  W.  Wang,  J.  Gumbart,  E.  Tajkhorshid,  E.  Villa,  C.  Chipot,  R. D.  Skeel,  L.  Kalé, and  K.  Schulten, J. Comput. Chem., 26, 1781–1802 (2005).
• [11]   J. B.  Klauda,  R. M.  Venable,  J. A.  Freites,  J. W.  O’Connor,  D. J.  Tobias,  C.  Mondragon-Ramirez,  I.  Vorobyov,  A. D.  MacKerell and  R.  W Pastor, J. Phys. Chem. B, 114, 7830–7843 (2010).
• [12]   J.  Henin,  G.  Fiorin,  C.  Chipot and  M. L.  Klein, J. Chem. Theory Comput., 6, 35–47 (2010).
• [13]   Y.  Miyazaki,  S.  Okazaki and  W.  Shinoda, Biochim. Biophys. Acta - Biomembr., 1864, 1409–1419 (2019).
• [14]   G.  Tesei,  M.  Vazdar,  M. R.  Jensen,  C.  Cragnell,  P. E.  Mason,  J.  Heyda,  M.  Skepö,  P.  Jungwirth and  M.  Lund, Proc. Natl. Acad. Sci. U. S. A, 114, 11428–11433 (2017).
• [15]   M. T. H.  Nguyen,  D.  Biriukov,  C.  Tempra,  K.  Baxova,  H.  Martinez-Seara,  H.  Evci,  V.  Singh,  R.  Šachl,  M.  Hof,  P.  Jungwirth,  M.  Javanainen and  M.  Vazdar, Langmuir, 38, 11284–11295 (2022).
• [16]   Y.  Miyazaki and  W.  Shinoda, Biochim. Biophys. Acta-Biomembr., 1864, 183955 (2022).

著者紹介

宮崎 裕介（博士（工学））

〔経歴〕2020年名古屋大学大学院工学研究科博士課程修了．2022年から現所属．〔専門〕分子シミュレーション．〔趣味〕音楽鑑賞．