Molecular chirality: A new approach from a dynamical point of view

Abstract

The double minimum potential (DMP), which Hund assumed to explain the quantum-mechanical stability of enantiomers, was discussed, by citing three typical examples of DMP: inversion, internal rotation, and puckering. They expanded the classical scope of chirality, as defined by Kelvin, and indicated that a new bridge could be formed between the three low-frequency DMP modes and the asymmetric syntheses of chiral molecules.

1. Introduction

Chirality plays important roles in many areas, including the living; animals and plants consist of some fundamental molecules like peptides and sugars, most of which exhibit conspicuous enantiomer excess (ee), a phenomenon referred to as “homochirality”, and its origin has been explored extensively, but has not been understood clearly; many explanations were proposed for it, but have still been subjected to critical debates. Most tools so far employed to “measure” chirality were based upon the rotation of the polarization of the light wave for inspection and have been applied even to materials of macroscopic sizes. The studies on such materials have yielded many interesting stuffs, some of which have proved to be indispensable for the modern human life. I shall, however, focus my research on molecules, namely on molecular chirality, in order to scrutinize the real essence of the chirality. According to a text book,¹⁾ Lord Kelvin defined chirality for the first time in 1904 as follows: “I call any geometrical figure, or group of points, chiral, and say that it has chirality if its image in a plane mirror ideally realized, cannot be brought to coincide with itself”. This definition has been widely accepted, and I shall also follow it closely in the present paper. It should, however, be pointed out that the definition was set up well before quantum mechanics appeared in 1925 and thus some modifications, or more properly stated, additions and/or extensions will be necessary, as demonstrated in the present paper.

In a previous paper,²⁾ I pointed out a characteristic behavior of a C₁ symmetry molecule, namely a molecule without any symmetry element. This type of a molecule has the components of the electric dipole moment along all the three principal axes of inertia: a, b, and c. As a result, the three types of rotational transitions are all allowed, resulting in an apparent violation of the parity selection rule. In order to clarify the origin of this important anomaly, I examined the dynamical response of a C₁ symmetry molecule to three microwave radiations, the frequencies of which were in resonance with three rotational transitions, one for each of the a, b, and c types and forming a closed cycle, by solving a time-dependent Schrödinger equation. The dynamical behavior of a C₁ molecule thus clarified led me to an idea, that the triple resonance scheme like the one I discussed could make it possible for us to determine the enantiomer excess; ee. To my great surprise and also pleasure, this naïve idea of mine was subsequently beautifully realized by John Doyle’s^3)–9) and Brooks Pate’s^10),11) groups.

As I briefly discussed in my paper, the characteristic behavior of a C₁ molecule originates from the mixed parity, where two important contributions to chirality: Hund’s tiny perturbation¹²⁾ and Lee-Yang’s parity violation¹³⁾ were formally taken into account. Hund assumed such perturbation terms in order to explain why enantiomers exist as stable molecules, but his assumption was too abstract so I wish I make the Hund perturbation as concrete as possible in the present paper. As I already mentioned previously, the characteristic behavior of a C₁ molecule I discovered seems to be closely related to Hund’s perturbations; I shall examine this important point as much in detail as possible in the present study, by citing a few molecules with some characteristic low-frequency modes as examples.

2. Double minimum potential

Kelvin’s definition of chirality is based upon a relation between a real substance and its mirror image, but we wish to replace it by a physical operation, which brings one enantiomer to the other in a clearly defined way. Apart from parity violation, the two enantiomers are completely equivalent except that their geometrical shapes are mirror images with each other, as Kelvin defined. I shall come back to this point below. The second problematic aspect of the Kelvin definition lies in that he did not specify relative position and/or orientation of the mirror and the subject: the molecule we are looking at. In order to remedy this point, it would be natural to employ the principal moments of inertia axes, which we designate as g, g′, and g′′, or, as done in many cases, we name a, b, and c according to the magnitudes of the principal moments of inertia: I_aa < I_bb < I_cc. The reflection on the g/g′ plane may be expressed as a product of inversion and the two-fold rotation about an axis perpendicular to the reflection plane as follows:   

\begin{equation} \boldsymbol{{\sigma}}_{gg'} = \mathbf{i} \times \mathbf{C}_{\mathbf{2}}{}^{(g'')}\quad (\text{$g$, $g'$, and $g''$ are cyclic}). \end{equation} [1]

It will be convenient to introduce a rectangular parallelepiped shown in Fig. 1, which we shall call the H box; it is defined by the three edges proportional to the three components of the electric dipole moment. One enantiomer may be allocated to one red-painted corner of the H box, and the reflections on the ab, bc, and ca planes transfer the reference enantiomer to the three corners indicated by an asterisk, and the subsequent two-fold rotations about the axis, c, a, and b, respectively, further the asterisks to the final “double-star” corner ✸ of the other enantiomer. The transformation from one enantiomer to the other is expressed by a route from the red corner to the double-star corner. There would be numerous or even infinite routes present, but we start with the simplest one: the double minimum potential (DMP), as depicted in Fig. 2.

Fig. 1.

The H box for a C₁ chiral molecule, defined by the principal inertial axis system. The three components of the electric dipole moment are indicated by thin arrows and the enantiomer we are looking at is indicated by a red point at a corner pointed by a thick arrow, which is the total electric dipole moment. The reflections on the ab, bc, and ca planes transfer the original enantiomer red corner to the three corners designated by stars, which end up by an appropriate two-fold rotation at the final corner symbolized by a “double” star. The transformation from one enantiomer to the other may be expressed by a route from the original red point to the final double star.

Fig. 2.

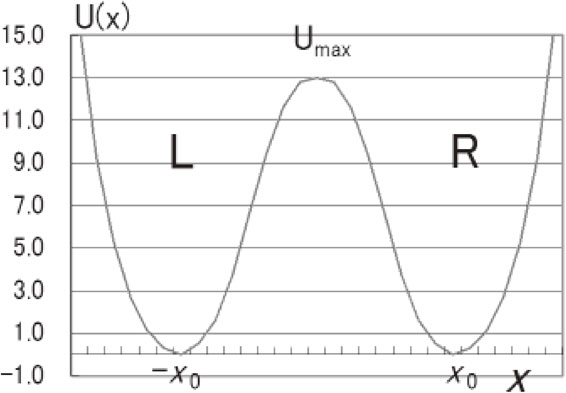
Double minimum potential (DMP) plotted against the coordinate x, which will be called the racemization coordinate. The potential function U(x) is an even function of x, with a potential maximum at the center x = 0. The two potential minima: L and R are mirror images with each other, located at x = −x₀ and +x₀, respectively, and separated by the potential maximum U_max at the center.

One minor comment is added here on the H box. As far as the molecule is completely isolated from the environment, the H box may be rotated in any way in space. When an external electric field E is applied along the space-fixed Z direction, we add the Stark effect terms to the Hamiltonian, which are proportional to the direction cosines: Φ_Zg, where g = a, b, or c, namely H_Stark = Σ_gμ_gEΦ_Zg.

Thanks to the inversion in the ammonia molecule, the double minimum problem has been extensively investigated, and we know now the eigenfunctions and eigenvalues of DMP quite well. It should be added that, when we simply say “inversion” in ammonia, it means “reflection” in the strict sense. Townes and Schawlow, for example, discussed the DMP problem in detail in their textbook on microwave spectroscopy.¹⁴⁾ When U_max is high, low-energy eigenstates tend to be paired with well-defined parities; + and −, respectively. When PV may be ignored, the two lowest eigenfunctions are almost exactly given by   

\begin{equation} |0+\rangle = [|\text{L}0\rangle + |\text{R}0\rangle]/\surd 2, \end{equation} [2a]

  

\begin{equation} |0-\rangle = [|\text{L}0\rangle - |\text{R}0\rangle]/\surd 2, \end{equation} [2b]

which may be reversed to   

\begin{equation} |\text{L}0\rangle = [|0+\rangle + |0-\rangle]/\surd 2, \end{equation} [3a]

  

\begin{equation} |\text{R}0\rangle = [|0+\rangle - |0-\rangle]/\surd 2, \end{equation} [3b]

where |L0⟩ and |R0⟩ denote the lowest states in the L and R minima, respectively. Townes and Schawlow gave a time-dependent solution. Suppose that a molecule lies in the L minimum at t = 0, as represented by Eq. [3a], and after t, its wavefunction becomes   

\begin{equation} \psi = [|0+\rangle + |0-\rangle\exp(2\pi i\nu t)]/\surd 2 \times \exp[(2\pi iW_{0}t)/\hbar]. \end{equation} [4]

When the time T required for the molecule to pass through the potential barrier, i.e., the tunneling time = 1/ν, is much longer than the measurement time t, ψ becomes   

\begin{align} \psi &= \{|\text{L}0\rangle + \pi i(t/T)[|\text{L}0\rangle - |\text{R}0\rangle]\} \exp[(2\pi iW_{0}t)/\hbar] \\ &\quad + \ldots. \end{align} [5]

The molecule thus remains in the L minimum essentially forever, and the parity is not defined, as we observe.

It should be noted that DMP discussed above is one-dimensional and thus we require two more coordinates to describe the motions of the entire molecule. The two coordinates, say y and z, are perpendicular to the x, crossing it at x = 0 and orthogonal each other. A unique atom i in the molecule (i.e., there are no other equivalent atoms) will have x_i = 0 at x = 0. A pair of equivalent atoms i and j will satisfy the conditions, which will differ for different systems. The followings represent the results obtained for the case of internal rotation and reflection as two operations for the molecule CH₂X–CH₂Y (For the details, see the next section). An example of a unique atom in the molecule is Y and of a pair of equivalent atoms is the two hydrogens in the CH₂Y group, and the coordinates of the two H’s may be expressed using α, β, γ as follows, by the structure of the molecule.

operation	H atoms	x = −x0	x = 0	x = +x0
internal  rotation:	i	α	+γ	−β
	j	β	−γ	−α
reflection:	i	α	0	−α
	j	β	0	−β

The two operations: internal rotation and reflection yield apparently different results, but the molecule occupies essentially equivalent quantum states. It is thus sensible to extend the Kelvin operation: mirror image or reflection so as to include both reflection and internal rotation.

We shall then extend the results obtained on the simple model of DMP to more general cases, in order to make the view of molecular chirality as complete as possible. We proceed toward the goal by asking several questions on the DMP, as listed below:

1. (1)    Potential barrier U_max

   What is the origin of U_max? Its shape, height, and so on.

2. (2)    Chiral transitions

   There must be transitions from the ground states to excited states, within one potential valley, and also cross transitions through the central potential barrier. Are such transitions actually observed?

3. (3)    Racemization coordinate x

   What is it? What does it represent? There must be more than one such coordinate, and then how are they related each other?

4. (4)    What is the racemization? How does the DMP model explain it?
5. (5)    The effects of environment on the racemization

   How do intermolecular interactions affect the racemization?

I thought that, in order to answer the questions mentioned above, it would be sensible to examine the dynamical behavior of molecules, which execute low-frequency and/or large-amplitude motions, because they give us a clear view on chirality, as described in the next section.

3. Low-frequency and/or large-amplitude intramolecular motions

I shall focus attention to two types of low-frequency and/or large-amplitude motions: internal rotation and puckering. As already mentioned, the “inversion” will also be of primary importance in the present problem, because it is equivalent to the reflection, and the real inversion requires further multiplication of the two-fold rotation, as expressed in Eq. [1], and in fact the ammonia “inversion” stands as a most famous example of DMP. There are many amines NH₂X and imines NHXY, which involve a nitrogen atom as a possible center of the “inversion”. However, these molecules are planar in most cases and thus not chiral, in spite of the fact that the peptide linkage XCO–NHY acts as a key backbone of the so-called bio-molecules.¹⁵⁾ In this respect, I should add a comment that the P atom has a stronger tendency to be pyramidal than the N atom does, so that we anticipate many P-containing chiral molecules. In fact, Wenjun Tang’s group,¹⁶⁾ for example, reported development of novel P-chiral phosphorus ligands for efficient transition-metal catalyzed reactions; a representative ligand is C₆H₄[OCH₂PH].

(1) H₂O₂ type molecules.

As is well known, the two HOO planes of H₂O₂ are not coplanar at the minima of the potential, but make the dihedral angle of 113.70°, and thus the molecule is chiral. A unique feature of this type of molecules lies in that both internal rotation and reflection transfer the molecule from one enantiomer form to the other, as shown in Fig. 3.

Fig. 3.

Hydrogen peroxide type molecule. Both internal rotation and reflection transform one enantiomer form to the other; namely the two operations are completely equivalent.

We mention another example of the same type: 1,3-difluoroallene, HFC=C=CHF, in which the two CHF planes are perpendicular to each other so that the molecule belongs to C₂ symmetry. We may think of internal rotation of the CHF about the C=C=C axis with respect to the other CHF, and the barrier to this internal rotation will be as high as electronic energy, and a similar consideration may hold for the reflection, so that the tunneling splitting will be quite small, making the enantiomers quite stable.

For a C₂ symmetry chiral molecule, the H box becomes a straight line, that is, consists of one coordinate. This is obviously insufficient to describe the behavior of a C₂ chiral molecule. For example, the racemization coordinate of H₂O₂ molecule is the dihedral angle between the two HOO planes, and angle is difficult to incorporate in one dimensional line. A similar remark holds for a C₃ symmetric-top chiral molecule.

(2) 1,2-disubstituted ethane derivatives.

CH₂X–CH₂Y, gauche forms; internal rotation.

We assume here that the substituents X and Y are different. The molecule of this form exists in trans and gauche in most cases, namely as rotational isomers. We are interested in only gauche; there are two equivalent gauche forms as a chiral pair and we entirely ignore trans in our discussion, namely we presume that no mixing occurs between energy levels of trans and gauche and that the two groups are well separated by a high potential barrier.

The projection of the gauche forms on a plane perpendicular to the C–C bond (the internal rotation axis) is displayed in Fig. 4. We start from the reference configuration I and transform it to the II by internal rotation through the cis form (i.e., the conformation where the C–X and the C–Y confront each other, and the path through the trans is neglected by the assumption.). We may also apply reflection to the I to arrive the III. The III conformation looks equivalent to the II, but differs from it in the numberings 3 and 4 of the two methylene hydrogens in the CH₂Y group and also in 1 and 2 in the CH₂X. If no further discrimination exists between H3 and H4 and between H1 and H2, the two conformations II and III are completely equivalent, and, even if interactions involving the nuclear spins are taken into account, the two conformations II and III are essentially degenerate in energy, and we may treat them identical. We may thus regard the internal rotation as a chiral operation; it differs from the reflection in that the “path” of internal rotation is clearly defined, whereas the reflection is defined by only the initial and final states of the operation (see the discussion on the atomic coordinates at the end of Sec. 2). It should be noted that there is a huge potential barrier between the II and the III, because we must exchange the C–H3 bond with the C–H4 bond and also C–H1 with C–H2, so that the tunneling splitting between the II and the III is quite small. The situation is similar for the pair: the I and the IV.

Fig. 4.

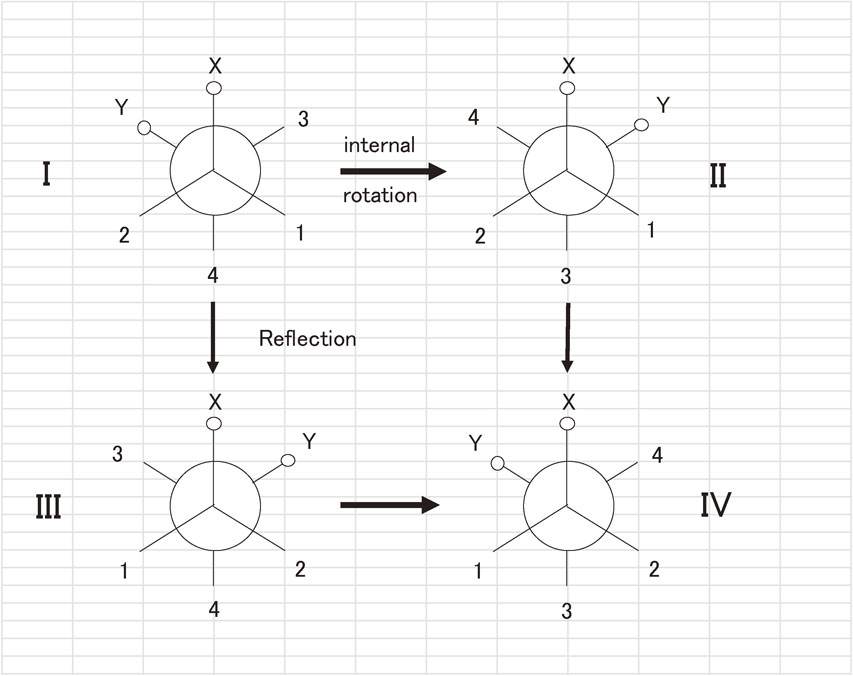
CH₂X–CH₂Y molecule projected on a plane perpendicular to the C–C bond.

In most cases, the reflection of a molecule involves high-energy paths. In the example discussed above, the reflection requires the exchange of two or four C–H bonds. It is likely that the reflection is an important, or even indispensable, operation to determine whether a molecule is chiral or not, but its real path will contain routes, which the molecule will not take because of high energy. On the other hand, low frequency and/or large amplitude motions transform a chiral molecule from a configuration to the other, in much the same way as the reflection does.

When the tunneling splitting between the I and the II and also between the III and the IV due to internal rotation is as small as that between the I and the III and between the II and the IV by reflection, we regard the four conformations equivalent with an average energy E₀ and set up the Hamiltonian matrix as follows:   

\begin{equation} \begin{array}{l} \begin{matrix} \quad\text{I} & \;\text{II} & \;\text{III} & \;\text{IV} \end{matrix} \\ \begin{bmatrix} E_{0} & a & b v 0\\ & E_{0} & 0 & b\\ & & E_{0} & a\\ & & & E_{0} \end{bmatrix}, \end{array} \end{equation} [6]

where a and b denote the effects of tunneling splitting by internal rotation and reflection, respectively, and the tunneling between the II and the III and also that between the I and the IV are neglected. The Hamiltonian matrix [6] is then diagonalized to give the eigenfunctions and the eigenvalues:   

\begin{align} |1\rangle = [|\text{I}\rangle + |\text{II}\rangle + |\text{III}\rangle + \text{IV}\rangle]/2,&\\\quad E_{1} = E_{0} + a + b,& \end{align} [7a]

  

\begin{align} |2\rangle = [|\text{I}\rangle + |\text{II}\rangle - |\text{III}\rangle - \text{IV}\rangle]/2,&\\\quad E_{2} = E_{0} + a - b,& \end{align} [7b]

  

\begin{align} |3\rangle = [|\text{I}\rangle - |\text{II}\rangle + |\text{III}\rangle - \text{IV}\rangle]/2,&\\\quad E_{3} = E_{0} - a + b,& \end{align} [7c]

  

\begin{align} |4\rangle = [|\text{I}\rangle - |\text{II}\rangle - |\text{III}\rangle + |\text{IV}\rangle]/2,&\\\quad E_{4} = E_{0} - a - b.& \end{align} [7d]

The two paths: internal rotation and reflection play roles independent with each other. In order to take into account the rotational motions, we must go back to the H box to write in the paths therein.

(3) Cyclobutane and its derivatives; puckering.

Four carbon atoms of cyclobutane connected by single bonds one by one form a four-membered ring, which is not planar at the equilibrium, but puckers. Each carbon atom is bonded to two H atoms, one C–H bond pointing nearly along the C₂ symmetry axis of the molecule and the other towards outside the ring, and the former is referred to as ax (axial) and the latter to as eq (equatorial). The ax and eq bonds exchange their roles when the molecule puckers; the “old” ax (upward pointing) becomes the “new” eq, whereas the “old” eq the “new” ax (pointing downward).

Cyclobutane is a simplest molecule, which executes puckering, and has thus been investigated extensively by infrared and Raman spectroscopy^17)–28) and by electron diffraction^24),25) during 1960’s up to 90’s, yielding the potential barrier to puckering to be about 500 cm⁻¹ and the equilibrium dihedral angle to be about 28°. Because it is nonpolar, no rotational transitions have been observed. Vogelsanger et al.,²⁹⁾ however, succeeded in detecting rotational spectra of a singly deuterated species and in assigning absorption lines observed for both the ax and eq d₁ forms by using Fourier transform microwave spectroscopy. Caminati et al.³⁰⁾ extended the study to the 1,1-d₂ species to determine the puckering splitting to be 95.2(37) MHz. My coworkers and I^31)–34) concurrently carried out millimeter-wave spectroscopy on the 1,2-d₂ trans and cis and 1,1,3,3-d₄ species of cyclobutane and confirmed that the 1,2-d₂ trans consisted of the ax-ax and the eq-eq forms and cis of the ax-eq and the eq-ax forms, as shown in Fig. 5.

Fig. 5.

Cyclobutane-1,2-d₂, trans and cis; a short bar denotes a C–D bond in the ax position and a long bar that in the eq position. The red real bar and the blue dotted bar designate that the chemical bonds are located above and below the ring, respectively. The puckering is indicated by double lines for upper bent C–C bonds. The trans form retains a C₂ symmetry axis during puckering, whereas in the cis form the principal inertial axes a and b rotate nearly 45° suddenly when the molecule starts to pucker.

From the chirality viewpoint, the puckering in cyclobutane looks similar to the “inversion” in ammonia; cyclobutane does not change its structure by puckering and thus achiral, according to the Kelvin convention extended to large amplitude motions as a racemization operation. The singly-deuterated species, which Vogelsanger et al. investigated, exist in either ax or eq, both of which are distinct stable species and thus are regarded as achiral, and Caminati’s 1,1-d₂ again not chiral. The 1,2-d₂ trans ax-ax and eq-eq species and the 1,1,3,3-d₄ species we spectroscopically studied are also achiral; the two species ax-ax and eq-eq of the 1,2-d₂ trans are independent molecules, namely they are not accompanied with any partner to be coincide with themselves and the 1,1,3,3-d₄ species does not change the structure by puckering. It should be noted that Caminati’s 1,1-d₂ and our 1,1,3,3-d₄ species consist of two equivalent, superimposable forms and their rotational spectra could be analyzed by setting up a 2 × 2 effective matrix for the two forms.

In sharp contrast with these, the 1,2-d₂ cis exists in either ax-eq or eq-ax, as shown in Fig. 5, and the two forms are physically equivalent and exchanged by puckering, but cannot be superimposed with each other, namely this species satisfies the requirement for chirality. I shall ignore the reflection in the following discussion, because, as we already find in a previous section, the reflection takes place in only energetically unfavorable path. The two deuterium atoms of the cis form may be replaced by other atom or group of atoms pair to produce “heavier” and/or much less flexible species, which will exist as stable chiral molecules. The rotational spectra of the 1,2-d₂ cis are complicated; one reason for the complication is due to the fact that the principal inertial axes a and b rotate by as much as 45° when the molecule starts to pucker from a planar form, as already mentioned.

The rotational motion is thus expected to be coupled with puckering. Hirota et al., in fact, required an elaborate Hamiltonian to reproduce the observed millimeter-wave spectra, namely they started from a 2 × 2 Hamiltonian matrix for the ax-eq and eq-ax states, with the tunneling splitting ±ΔE/2 in the diagonal block and [(R_x/2) − (R_xx/2)J²][J_x, J_y]₊ − (R_xz/4)[J_z², [J_x, J_y]₊]₊ − (R_xy/4)[(J_x² − J_y²), [J_x, J_y]₊]₊ + (R_z/2)[J_y, J_z]₊ in the off-diagonal block, where the z axis is taken to be nearly perpendicular to the “molecular plane”, whereas x and y stand for the “in-plane” coordinates, with y being antisymmetric to the puckering. The symbol [J_g, J_g′]₊ denotes the anti-commutator: J_gJ_g′ + J_g′J_g.

The puckering splitting ΔE = 86.21(40) MHz thus obtained may be compared with 95.2(37) and 34.47(10) MHz for the Caminati’s 1,1-d₂ and our 1,1,3,3-d₄ species, respectively. The puckering splitting is obviously a tunneling splitting, and thus decreases rapidly with the mass and/or size of the substituents. Therefore we may expect to have a large number of stable chiral molecules with much varieties. It should be noted that only the cis species is chiral among di-substituted ones, a remarkable “selective” property of the cyclobutane derivatives.

A number of investigations have recently been carried out on the olefin [2+2] photocycloaddition reactions, as summarized in an extensive review by Bach and his collaborators.³⁵⁾ Although some modifications also exist, the essential part of these reactions may be expressed as follows:   

Namely the central backbone of the products is cyclobutane, and a few substituents and/or the associated ring chain in the starting compounds will make the structure of the resultant molecules stiff and/or heavy sufficiently as a stable chiral molecule. In fact, most reactions discussed in ref. 35 are regio-selective and/or stereo-selective to yield a large variety of chiral molecules.

Discussion and conclusion

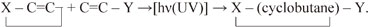The majority of chiral molecules are of C₁ symmetry, i.e., involve no symmetry elements. Nevertheless, when we look these molecules carefully, we find they consist of two equivalent elements: enantiomers, which often give rise to unique symmetry for the molecules as a whole, and such a symmetry plays important roles in racemization processes and other dynamical behaviors of the molecular system. We should pay much more attention to the multi-racemization processes; symmetry consideration would provide us with good guide for us in this respect. On the other hand, it would be also a good question to ask the possible roles of symmetry breaking in molecular chirality.

The parity violation PV pointed out by Lee and Yang¹³⁾ has not yet been proven to exist in the framework of molecular spectroscopy. We thus like to ask for a possibility that PV may show up its effect only in a new feature of molecules which has not been thought of hither-to-fore.

The present study pointed out that Kelvin’s definition of chirality needs to be extended so as to include the effects of quantum mechanics and proposed to include low-frequency and/or large-amplitude motions in the definition of molecular chirality as a supplementary to Kelvin’s reflection. It also made clear that there exists a close relation between low-frequency intra-molecular motions and asymmetry syntheses. This relation suggests two widely separated fields of science may be merged to form a new promising large area in future.

Acknowledgments

I express sincere gratitude to Professor Toshimitsu Yamazaki and Professor Makoto Kobayashi for stimulating discussions.

References

• 1)  Barron, L.D. (2004) Molecular Light Scattering and Optical Activity. 2nd ed., revised and enlarged, Cambridge University Press, Cambridge.
• 2)   Hirota,  E. (2012) Triple resonance for a three-level system of a chiral molecule. Proc. Jpn. Acad. Ser. B 88, 120–128.
• 3)   Patterson,  D.,  Schnell,  M. and  Doyle,  J.M. (2013) Enantiomer-specific detection of chiral molecules via microwave spectroscopy. Nature 497, 475–477.
• 4)   Patterson,  D. and  Doyle,  J.M. (2013) Sensitive chiral analysis via microwave three-wave mixing. Phys. Rev. Lett. 111, 023008.
• 5)   Shubert,  V.A.,  Schmitz,  D.,  Patterson,  D.,  Doyle,  J.M. and  Schnell,  M. (2014) Identifying enantiomers in mixtures of chiral molecules with broadband microwave spectroscopy. Angew. Chem. Int. Ed. 53, 1152–1155.
• 6)   Patterson,  D. and  Schnell,  M. (2014) New studies on molecular chirality: enantiomer differentiation and determination of enantiomeric excess and molecular handedness. Phys. Chem. Chem. Phys. 16, 11114–11123.
• 7)   Shubert,  V.A.,  Schmitz,  D. and  Schnell,  M. (2014) Enantiomer-sensitive investigations of chiral molecule containing two stereogenic centers — microwave three-wave mixing of menthone. J. Mol. Spectrosc. 300, 31–36.
• 8)   Medcraft,  C.,  Wolf,  R. and  Schnell,  M. (2014) High-resolution spectroscopy of the chiral metal complex [CpRe(CH₃)(CO)(NO)]: a potential candidate for probing parity violation. Angew. Chem. Int. Ed. 53, 11656–11659.
• 9)   Shubert,  V.A.,  Schmitz,  D.,  Medcraft,  C.,  Krin,  A.,  Patterson,  D.,  Doyle,  J.M. and  Schnell,  M. (2015) Rotational spectroscopy and three-wave mixing of 4-carvomenthenol: a technical guide to measuring chirality in the microwave regime. J. Chem. Phys. 142, 214201.
• 10)   Lobsiger,  S.,  Perez,  C.,  Evangelisti,  L.,  Lehmann,  K.K. and  Pate,  B.H. (2015) Molecular structure and chirality detection by Fourier transform microwave spectroscopy. J. Phys. Chem. Lett. 6, 196–200.
• 11)   Seifert,  N.,  Pérez,  C.,  Neill,  J.L.,  Pate,  B.H.,  Valeico-López,  M.,  Lesarri,  A.,  Concinero,  E. and  Castaño,  F. (2015) Chiral recognition and atropisomerism in the sevoflurane dimer. Phys. Chem. Chem. Phys. 17, 18282–18287.
• 12)   Hund,  F. (1927) Zur Deutung der Molekelspektren. III. Bemerkungen über das Schwingungs- und Rotationsspektrum bei Molekeln mit mehr als zwei Kernen. Z. Phys. 43, 805–826.
• 13)   Lee,  T.D. and  Yang,  C.N. (1956) Question of parity conservation in weak interactions. Phys. Rev. 104, 254–258.
• 14)  Townes, C.H. and Schawlow, A.L. (1955) Microwave Spectroscopy. McGraw-Hill Book Co., Inc., New York.
• 15)   Kawashima,  Y.,  Usami,  T.,  Ohashi,  N.,  Suenram,  R.D.,  Hougen,  J.T. and  Hirota,  E. (2006) Dynamical structure of peptide molecues. Acc. Chem. Res. 39, 216–220.
• 16)  A most recent publication is cited here:  Hu,  N.,  Li,  K.,  Wang,  Z. and  Tang,  W. (2016) Synthesis of chiral 1,4-benzodioxanes and chormans by enantioselective palladium-catalysed alkene aryloxyarylation reactions. Angew. Chem. Int. Ed. 55, 5044–5048.
• 17)   Lord,  R.C. and  Stoicheff,  B.P. (1962) High resolution Raman spectroscopy of gases: XV. Rotational spectrum and molecular structure of cyclobutane. Can. J. Phys. 40, 725–731.
• 18)   Lord,  R.C. and  Nakagawa,  I. (1963) Normal vibrations, potential constants, and vibration-rotation interaction constants in cyclobutane and cyclobutane-d₈. J. Chem. Phys. 39, 2951–2965.
• 19)   Ueda,  T. and  Shimanouchi,  T. (1968) Dihedral angle and ring-puckering potential of cyclobutane. J. Chem. Phys. 49, 470–471.
• 20)   Stone,  J.M.R. and  Mills,  I.M. (1970) Puckering structure in the infrared spectrum of cyclobutane. Mol. Phys. 18, 631–652.
• 21)   Miller,  F.A. and  Capwell,  R.J. (1971) The ring-puckering vibration of cyclobutane and cyclobutane-d₈ in their gas phase Raman and infrared spectra. Spectrochim. Acta, Part A 27, 947–956.
• 22)   Miller,  F.A.,  Capwell,  R.J.,  Lord,  R.C. and  Rea,  D.G. (1972) Infrared and Raman spectra of cyclobutane and cyclobugtane-d₈. Spectrochim. Acta, Part A 28, 603–618.
• 23)   Malloy,  T.B. Jr. and  Lafferty,  W.J. (1975) On the barriers to planarity and the isotope effect in cyclobutane and cyclobutane-d₈. J. Mol. Spectrosc. 54, 20–38.
• 24)   Egawa,  T.,  Fukuyama,  T.,  Yamamoto,  S.,  Takabayashi,  F.,  Kambara,  H.,  Ueda,  T. and  Kuchitsu,  K. (1987) Molecular structure and puckering potential function of cyclobutane studied by gas electron diffraction and infrared spectroscopy. J. Chem. Phys. 86, 6018–6026.
• 25)   Egawa,  T.,  Yamamoto,  S.,  Ueda,  T. and  Kuchitsu,  K. (1987) Two-dimensional analysis of the ring-puckering and methylene-rocking modes of cyclobutane. J. Mol. Spectrosc. 126, 231–239.
• 26)   Egawa,  T.,  Yamamoto,  S. and  Kuchitsu,  K. (1988) High-resolution infrared spectra of the ν₁₄ and ν₁₆ bands for cyclobutane. J. Mol. Spectrosc. 129, 72–85.
• 27)   Champion,  R.,  Godfrey,  P.D. and  Bettens,  F.L. (1992) A semirigid bender analysis of ring-puckering in cyclobutane. J. Mol. Spectrosc. 155, 18–24.
• 28)   Li,  H.,  Miller,  C.C. and  Phillips,  L.A. (1994) High resolution infrared spectroscopy of cyclobutane: A study of vibrational mode coupling involving large amplitude, low frequency modes. J. Chem. Phys. 100, 8590–8601.
• 29)   Vogelsanger,  B.,  Caminati,  W. and  Bauder,  A. (1987) The pure rotational spectrum of cyclobutane-d₁ observed by microwave Fourier transform spectroscopy. Chem. Phys. Lett. 141, 245–250.
• 30)   Caminati,  W.,  Vogelsanger,  B.,  Meyer,  R.,  Grassi,  G. and  Bauder,  A. (1988) Rotational spectrum, dipole moment, and ring-puckering potential of cyclobutane-1,1-d₂. J. Mol. Spectrosc. 131, 172–184.
• 31)   Hirota,  E.,  Endo,  Y.,  Fujitake,  M.,  Della,  E.W.,  Pigou,  P.E. and  Chickos,  J.S. (1988) Development of millimeter- and submillimeter-wave spectroscopy and its application to isotopically-substituted nonpolar molecules, deuterated cubane and deuterated cyclobutanes. J. Mol. Struct. 190, 235–258.
• 32)   Hirota,  E.,  Endo,  Y. and  Chickos,  J.S. (1987) The microwave spectra of deuterated cyclobutanes. IMS Ann. Rev. 35–36.
• 33)   Hirota,  E.,  Fujitake,  M. and  Chickos,  J.S. (1988) The microwave spectra of cis-cyclobutane-1,2-d₂ and cyclobutane-1,1,3,3-d₄. IMS Ann. Rev. 39.
• 34)   Hirota,  E.,  Fujitake,  M. and  Chickos,  J.S. (1989) Microwave spectrum of cis-cyclobutane-1,2-d₂ perturbed by the puckering vibration. IMS Ann. Rev. 42–43.
• 35)   Poplata,  S.,  Tröster,  A.,  Zou,  Y.-Q. and  Bach,  Th. (2016) Recent advances in the synthesis of cyclobutanes by olefin [2+2] photocycloaddition reactions. Chem. Rev. 116, 9748–9815.