Review of plasma turbulence experiments

Abstract

Understandings of turbulent plasma have been developed along with nuclear fusion research for more than a half century. Long international research has produced discoveries concerning turbulent plasma that allow us to notice the hidden nature and physics questions that could contribute to other scientific fields and the development of technologies. Guiding concepts have been established up to now that stimulate investigations on turbulent plasma. Research based on concepts concerning symmetry breaking and global linkage requires observing the entire field of plasma turbulence for an ultimate understanding of plasma. This article reviews the achievements as well as contemporary problems regarding turbulence experiments associated with strongly magnetized plasmas in the last and present century, and introduces forthcoming experimental issues, including new diagnostics and physics-oriented devices related to plasma turbulence.

1. Introduction

Plasma is a state of matter ubiquitously observed in the nature of the universe. Plasma features strong nonlinearity and non-equilibrium that results in continuous variation while maintaining the overall identity of structure, but occasionally producing abrupt changes in its entire structure. Plasma often occurs in a turbulence state where incessant annihilations and creations of fleeting fluctuations and structures should proceed in its steady background field. The transient, but invariant, properties give plasma a place in typical systems on which research advances our understanding of a major concept of natural science: how nature grows, as well as the ultimate elements of nature.

One of the most challenging applications of plasma is to realize a sun-like object on the ground, by confining plasma in a magnetic field container, where nuclear fusion reactions can occur in a controlled manner. Since the 1960’s international efforts have been made in pursuit of an improved confinement plasma to achieve a burning state more economically. This has not been easy, however, because turbulence forces plasma to escape quickly from any magnetic container. In other words, the confinement was much worse than the simple expectation of the transport induced by particle collisions. Numerous experimental devices have been constructed worldwide, like upsizing the plasma volume and the magnetic field strength. International efforts have been successful concerning the acquisition of higher plasma performance while providing empirical scaling laws to predict the relation between the device parameters and the plasma performance. Finally, after more than a half century, a famous project, ‘International Thermonuclear Experimental Reactor (ITER)’, has started in France through an international collaboration that includes Japan.

Concerning the long-term struggle toward ITER, many findings related to turbulence-related phenomena have been obtained to stimulate modern plasma physics together with the development of plasma diagnostics using microwaves,^1),2) ion beams,³⁾ and spectroscopies,⁴⁾ even though the diagnostics cover only a portion of the plasma turbulence field. Various discoveries have revealed the hidden nature of turbulent plasmas, including two distinguished phenomena as well as turbulence-driven transport. One is an H-mode transition⁵⁾ to manifest the bifurcation nature of a plasma and to help us to recognize the roles of electric fields (flows) of turbulent plasma.⁶⁾ The other is axial field generation from turbulence, such as zonal flows and magnetic fields^7),8) to demonstrate the importance of the structural generation processes in turbulence.

Further investigations with advanced diagnostics and analyses have disclosed mysterious functions of plasma turbulence sustained by mutual interactions between ephemeral fluctuations and structures over a wide range of scales (or called cross-scale coupling here), such as the intricate behavior of entire structural bifurcations,⁹⁾ symmetry-breaking phenomena predicted in theories and simulations,¹⁰⁾ as well as a global linkage between distant positions, for example, the core and the edge.¹¹⁾ These issues still remain open questions, providing wide academic challenges and impacts to other fields of natural science, as one of the most challenging subjects, ‘a state far from equilibrium’, in the modern physics, as well as to nuclear fusion research as its background physics.

Various unsolved issues should be illuminated in research fields based on modern views of turbulent plasma, symmetry breaking and global linkage as key guiding concepts to understand the structural formation and dynamics of turbulent plasmas. Such research can be carried out in a special device where entire plasma measurements are realized to uncover the reality of plasma turbulence. This article presents a brief review of the physical topics discovered through plasma turbulence research, e.g., drift-wave turbulence, transport barriers, and zonal flows and fields, along with a description of the modern concept and unsolved problems, and introduces forthcoming issues concerning an ultimate principle understanding of plasma turbulence.

2. Fundamental discoveries in turbulent plasmas

2.1. Turbulence-driven transport.

The tokamak configuration is the leading concept to confine plasma in a magnetic-field container. The tokamak was invented in Russia, and its study has been pursued worldwide since its achievement of high temperature and density in the 1970’s. The tokamak configuration is characterized by magnetic field configurations having a torus shape, as well as stellarators. Their difference exists concerning the following point: tokamaks require an internal plasma current to generate a poloidal field necessary to confine plasma, while the stellarators generate it with external coils. The magnetic field lines of torus devices, as shown in Fig. 1(a), form nested flux surfaces that confine the plasma inside. The magnetic flux surface can be labeled by its effective radial coordinate. The temperature and density of torus plasmas are usually expressed as a decreasing function of the effective radial coordinate.

Fig. 1.

(a) Schematic view of the magnetic field configuration of a tokamak, and the cross-section of the plasma. The magnetic-field lines form a nested surface, termed a magnetic flux surface, to confine the plasma inside. The torus shape of the magnetic field results in a stronger magnetic field on the inside of the torus to work towards stabilizing instabilities. (b) Asymmetry in density fluctuations on the weak and strong field sides.²⁴⁾ The density fluctuation spectrum on the weak field side is found to be larger in the frequency range of around ∼100 kHz than that on the strong field side. The density fluctuations are measured with a heavy ion beam probe in a tokamak.

From the early days of research concerning magnetic confinement fusion, the confinement time has been known to be worse than those expected from collisional transport. The cause was ascribed to the fact that the plasma should be in such a turbulence that enhances the transport.^12)–14) The first evidence concerning this point was obtained using microwave scattering measurements in small-size tokamaks, to show the existence of broad-band fluctuations around certain frequencies (∼100 kHz).^1),2) The frequency range was found to correspond to drift waves caused by inhomogeneity of the plasma density and the temperature. This hypothesis was confirmed in an inter-device comparison to show that the turbulence saturation level should increase, as in proportion to the inhomogeneity of the density,¹⁵⁾ so as to enhance the degradation of plasma confinement.¹⁶⁾

Nowadays, the cause of this turbulence is known to be drift-waves, although the responsible modes of drift-wave instabilities for turbulence has not yet been identified, such as a trapped electron mode,¹⁷⁾ an ion temperature gradient mode¹⁸⁾ and so on. Later developments of diagnostics revealed the fundamental characteristics of the fluctuations of tokamak plasmas, such as the dispersion relation,¹⁹⁾ and the radial profile of the turbulence amplitude.²⁰⁾ A quantitative comparison was made between the confinement and turbulence-driven transport, which suggested that the turbulence-driven flux could be sufficient to explain the confinement.²¹⁾

However, the further development of turbulence diagnostics revealed an important property of torus plasma turbulence, that is, the ballooning nature,²²⁾ the asymmetry of the turbulence strength on the weak and strong field side of a tokamak. Fluctuation measurements of the electron temperature and density using electron cyclotron emission (ECE) detection²³⁾ and a heavy ion beam probe (HIBP)²⁴⁾ showed the existence of a clear asymmetry in the turbulence field of the plasm interior. Figure 1(b) shows the experimental results: that the fluctuations on the weak field side should be much larger, as is expected in theories, in the frequency range of around ∼100 kHz. Recent observations in TJ-K stellarator using probes clearly showed that the turbulence and turbulence-driven transport should be asymmetric so as to be localized at a particular poloidal position dependent on the local structure of the three-dimensional magnetic configuration of the stellarator.²⁵⁾

These observations demonstrate that the assumption of symmetry on the magnetic flux surface should be broken for plasma turbulence. Thus, a single-point measurement is not sufficient for evaluating the turbulence-driven fluxes and understanding the plasma turbulence and its related phenomena. Moreover, the asymmetric property of turbulence should induce plasma currents and flows, which was first pointed out by Pfirsch and Schlüter.²⁶⁾ The induced currents and flows could regulate the plasma structure and dynamics toward equilibrium,²⁷⁾ and could reflexively affect the plasma turbulence. A model was actually proposed that the symmetry-breaking of turbulence or turbulence-driven flux could be a cause of the structural bifurcation of plasma, like the H-mode transition, described in the following subsection.²⁸⁾ Symmetry-breaking is an essential ingredient to understand the structure and dynamics of turbulent plasmas.

2.2. Role on an electric field on transport — Barrier formation.

The high confinement (H-) mode is a phenomenon that reveals that the plasma is a state of matter to bifurcate, that a mesoscale layer is suddenly created in the plasma edge region where turbulence and its transport are reduced.^5),29) A discovery in 1982 provided a way to achieve better plasma confinement, and to realize a more economic reactor. Thus, this discovery had an outstanding impact on fusion research, and stimulated the following findings of new improved confinement modes of torus plasmas³⁰⁾: such as super-shot,³¹⁾ internal transport barrier,^32)–38) RI-mode,³⁹⁾ and High Density H-mode.⁴⁰⁾ Moreover, it brought a new trend in physics research, after a theory was proposed by Itoh in 1988 to explain the H-mode transition.⁶⁾ This excited interest concerning the role of electric fields or plasma flows, which had never been paid attention in those days, since the magnetic field was thought to be essential to determine the confinement property. Note that perpendicular plasma flows to a magnetic field is connected to the electric field through the well-known E × B-drift, where E and B are the electric and magnetic field, respectively.

The theory ascribed the bifurcation nature of the H-mode to the property of a radial electric field, E_r, spontaneously generated in plasma.^6),41),42) The generation of a radial electric field obeys the equation, ε_⊥ε₀(∂E_r/∂t) = −j_r(E_r), where ε₀, ε_⊥⁴³⁾ and j_r(E_r) are the vacuum permittivity, the dielectric constant of the plasma and the radial current, respectively. The nonlinear dependence of the radial current on radial electric field can give multiple solutions in a steady state; i.e., j_r(E_r) = 0. The theory assumed that the H-mode transition (from L-mode) should correspond to that between two stable solutions, corresponding to the L- and H-modes, where the L-mode means the state of lower confinement before the H-mode transition. In addition, the cause of turbulence reduction was ascribed to the large electric field shear created in the interface layer of the two branches of E_r in several theories.^44)–46)

Itoh’s model was confirmed concerning the forced transition to the H-mode, where the external biased electrode inserted into the plasma edge was used to control the shear of the radial electric field.^47)–49) In the spontaneous H-mode transition, the formation of a sheared radial electric field was verified by an indirect measurement with a spectroscopic method.^50),51) However, the electric field is deduced using the radial force balance equation,   

\begin{equation*} \frac{1}{Zn_{e}}\frac{\partial P_{i}}{\partial r} = E_{r} + (v \times B)_{r}, \end{equation*}

which indicates the causal relation between the radial electric field and the pressure gradient. The variables (Z, n_e, v, B, and P_i), represent the effective change of the ions, electron density, plasma velocity, magnetic field, and ion pressure, respectively, In other words, the increased pressure gradient in the H-mode can result for making the electric field more negative to enhance the sheared electric field if the plasma velocities are neglected.

The causality problem was solved in the discovery of the internal transport barrier in a stellarator named Compact Helical System (CHS).³⁵⁾ The unique feature of the CHS device, whose major and minor radii are 1.0 m and 0.2 m, respectively, was the installation of an HIBP, by adopting an advanced method termed active trajectory control.^52),53) In addition, HIBP is the only one diagnostics procedure that can measure the electrostatic potential, magnetic field, and their fluctuations, directly in a magnetized plasma of high temperature as well as the electron density and its fluctuations. The HIBP measurements successfully revealed various hidden natures of a magnetized plasma to stimulate the modern concepts of a turbulent plasma, associated with the bifurcation nature, and axial field generation shown in the next subsection.

In transport barrier formation the time scale of the radial electric field transition was observed to be much faster, a few dozen microseconds, in contrast to the confinement time of a few milliseconds. Therefore, the radial electric field is able to trigger transport barrier formation.^54)–56) After the transition, a stronger electric field shear is created in the interface layer between two bifurcated branches of the radial electric field, as shown in Fig. 2, to reduce turbulence transport. Moreover, the sign of the radial electric field is opposite to that obeying the radial force balance equation. This fact denies the linkage with the ion pressure gradient. Furthermore, the time scale of the observed transition had a good agreement with that expected in neoclassical theory.^57),58) Thus, the bifurcation nature of radial electric field should originate from the neoclassical transport or collisional part of cross-field transport. It is concluded more generally that the E_r-bifurcation property is the cause of transport barrier formation.

Fig. 2.

Formation of an internal transport barrier in a stellarator.³⁵⁾ (a) Radial profile of potential and density fluctuations measured with a heavy ion beam probe (top). The density fluctuations are reduced at the interface of two bifurcated branches of a radial electric field. The radial electric field and its shear are evaluated from the measured potential (bottom). A strong shear is created at the interface layer between two branches of the radial electric field, and the strong shear works to reduce the fluctuations to create the transport barrier. The black dashed lines indicate the profiles without the interface. (b) Causal linkage between the radial electric field transition and annihilation of the transport barrier. The potential inside the barrier position shows a rapid drop (or the annihilation of the interface) on a timescale of a few dozen microseconds.⁵⁶⁾ The annihilation is found to cause a rapid increase in the fluctuations (or barrier annihilation), demonstrating that the radial electric field shear is the cause of transport barrier formation.

Another important finding is that the E_r-bifurcation nature should give birth to another interesting phenomenon, stationary self-excited oscillations composed of repetitive transitions between the bifurcated states; for example, edge localized modes (ELMs) can be regarded as the one between the L- and H-mode.^59),60) For fusion applications the ELMs have been intensively studied since the stored energy is released with a breakdown of the barrier during an ELMy pulse, which causes severe damages to the wall surrounding the plasma. In the CHS stellerator, a dynamic behavior, termed here electric pulsation, was discovered to be caused by the E_r-bifurcation nature.⁶¹⁾ Figure 3 shows the most drastic patterns of the electric pulsation and its details. The plasma potential exhibits violent activities, or quasi-periodic rises and falls in a few dozen microsconds, as shown in Fig. 3, while the plasma macroscopic density appears to almost be constant during pulsation. In other words, successive immanent activities can proceed in an apparently quiet plasma in the observation of macroscopic quantities. Moreover, a further mysterious finding concerning the electric pulsation is a global linkage between the core and the edge; the edge density simultaneously falls (or rises) at the same time scale with rises (or falls) of the central potential (see Fig. 3(c)), while the potential pulse is observed to propagate outward on a faster time scale than the diffusive one to determine the confinement.

Fig. 3.

Self-excited oscillatory state, termed electric pulsation, discovered in the CHS stellarator. (a) Temporal evolution of the central potential measured with an HIBP. The pulsation occurs quasi-periodically without significant changes in the line-integrated density. The pulsation is regarded as being repetitive transitions between bifurcated states. (b) Typical evolution of the potential profile during a cycle of pulsation. The profiles are reconstructed with a conditionally-averaged technique. It is found that the potential profile should evolve through several bifurcated states during a pulse. For example, the profile at t = 300 µs is identical to that of the internal transport barrier shown in Fig. 2. (c) Global linkage between the central potential and the detected beam intensity measured with two HIBPs. Both quantities show simultaneous changes, in spite of their distance being comparable to the plasma radius, showing the instantaneous propagation of a violent event happening at the plasma center. (d) Time scales of changes in the potential and detected beam intensity of HIBP. The time scales are found to be a dozen to one hundred microseconds, which are much faster than the confinement time of a few milliseconds. The timescales are evaluated with a fitting of the function form, tanh(t/τ), and the beam intensity reflects the local electron density.

2.3. Axial field generation — Zonal flows and field.

A paper entitled “Turbulence may sink titanic reactor” was published in 1996, while having a sensational impact on fusion research: plasma should not be burned in ITER.⁶²⁾ The prediction was based on a turbulence simulation. It was expected that the result may be caused by an incomplete treatment of the closure in the simulation, which neglected the generation of mesoscale flows, zonal flows, due to the turbulence.^63)–65) The Hasegawa-Mima equation proposed in 1977 to describe the plasma turbulence⁶⁶⁾ predicted the existence of zonal flows in torus plasmas. On the other hand, the Charney equation used to describe Rossby-wave turbulence in a rotating planet atmosphere is known to be identical to the above equation. Further, a simulation of the Jovian atmosphere, based on the equation, predicted the corresponding structure to zonal flows or the Jovian belts, which obviously exist.⁶⁷⁾ Therefore, the sensational prediction elevated a question in the 1970’s: if zonal flows should exist in torus plasmas or not, to a crucial and urgent question in fusion research.

Zonal flows are symmetric flows that circulate around the magnetic axis, while changing the flow direction as a function of the radius. An important fact concerning the zonal flows is that they do not provide any contribution to cross-field transport owing to their circulating nature. The zonal flows generated from microscale turbulence through the Reynolds stress, v∇v-nonlinearity in the Eulerian derivative, therefore, assuming that energy conservation between them, the confinement is improved if the turbulence (microscale fluctuations) energy goes to zonal flows. Moreover, zonal flows have their own shear to regulate turbulence, or reduce the microscopic turbulence that drives the cross-field transport.

The first experiment was carried out to search for zonal flows in CHS. The electric field was directly measured at two toroidal locations using three local potential values measured with twin HIBPs (see Fig. 4(a)). Identification was attempted in an electron cyclotron resonance (ECR) heated plasma that tended to be free from MHD activities to provide an easier environment to detect fluctuations. Moreover, the observation point was carefully chosen at the position ($\bar{r} = 12$ cm), which gave a maximum signal-to-noise ratio for the HIBP measurement of the electric field. Figure 4 shows the spectrum of the measured electric field fluctuation. Twin HIBP measurements confirmed that a low-frequency fluctuation of less than ∼1 kHz showed a long-distance correlation, one of the characteristics of zonal flows to satisfy. Correlation analysis confirmed, as shown in Fig. 4, that the low-frequency fluctuations should have a sinusoidal structure of a finite radial wavelength of ∼1.5 cm ($ \sim \sqrt{a\rho _{i}} $) in mesoscale, and that the structure should decay in a timescale of ∼1.5 ms, where a and ρ_i represent the plasma minor radius and the ion Lamor radius, respectively.

Fig. 4.

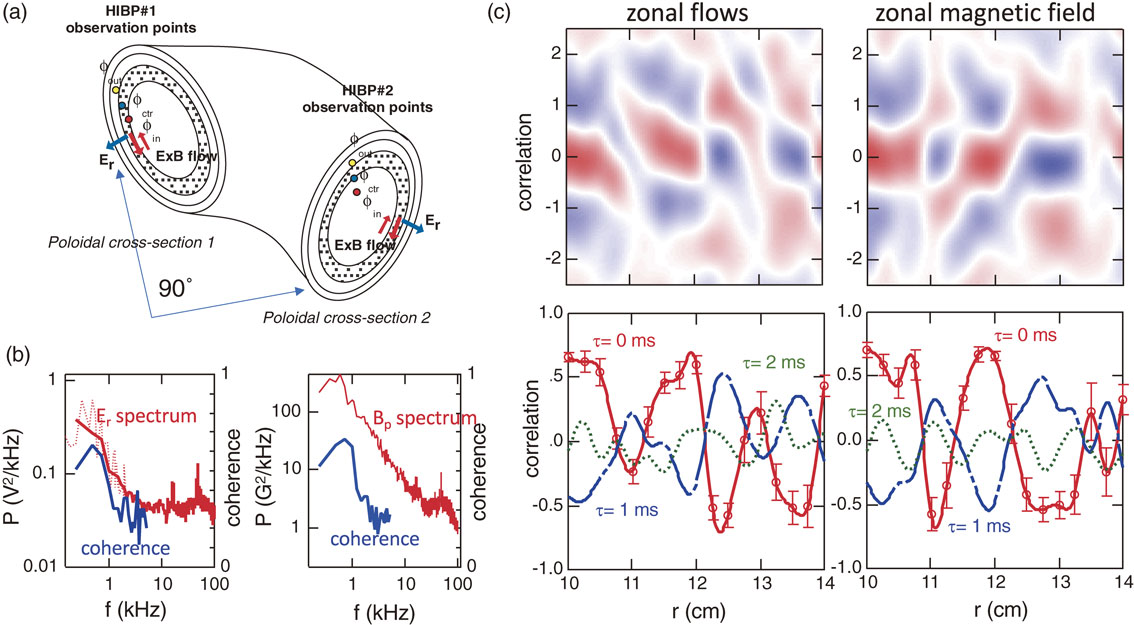
Zonal flows and field in the CHS stellarator. (a) Measurement configuration of twin HIBPs. Each HIBP can measure two plasma cross-sections and can examine the long-distance correlation of fluctuations. (b) Spectra of electric and magnetic field fluctuations. The fluctuations at a frequency of less than ∼1 kHz shows a long-range correlation between two positions that the HIBPs measure. (c) Structures of the zonal flows and fields evaluated with a correlation function, defined as c(r + ρ, t + τ) = ⟨f(r + ρ, t + τ)f(r, t)⟩/⟨|f(r + ρ, t + τ)|⟩⟨|f(r, t)|⟩, where ⟨ ⟩ means the temporal average, where ρ and τ are the radial distance between the observation points and the delay time, respectively. The analysis shows that the radial wavelength of the zonal structure should be ∼1.5 cm. The correlation becomes smaller as time passes, indicating that the lifetimes of the zonal flows and fields should be ∼1.5 ms.

Several theories were also proposed to predict the existence of zonal magnetic fields, as well as zonal flows, in torus plasmas.^64),68),69) As is similar to the case of zonal flows, measurements of the local magnetic field were performed with the twin HIBPs in CHS. Before each measurement, a formula was obtained to connect the beam movement with the magnetic field. The difference between the beam displacements on the neighboring detectors, $\Delta \mathop {\tilde{\phi }}\nolimits_{D}$, can be related with a local magnetic field as,⁷⁰⁾ $\mathop {\tilde{B}}\nolimits_{ \bot } = \alpha _{B}\Delta \mathop {\tilde{\psi }}\nolimits_{D}$, where $\mathop {\tilde{B}}\nolimits_{ \bot }$, α_B and $\Delta \mathop {\tilde{\psi }}\nolimits_{D}$ are magnetic field fluctuations perpendicular to both the magnetic field and the beam direction, a constant and the toroidal angle displacement of the beam, respectively. Using the above formula, a magnetic field fluctuation of less than ∼1 kHz was found to have a long-range correlation. The correlation analysis showed that the structure of the fluctuations in the frequency range should have a symmetric structure around the magnetic field axis with a radial structure on the mesoscale.⁸⁾ Finally, as shown in Fig. 4(c), the existence of zonal magnetic fields was confirmed similarly to the zonal flows. This observation demonstrates that the turbulence should really generate a structured magnetic field.

3. Modern issues in turbulent plasma

3.1. Visualization of cross-scale couplings.

Various discoveries have demonstrated that fundamental structures and fluctuations are present over a wide range of scale in turbulence plasmas, which play their own roles in structure formation. The fundamental elements, e.g., drift-waves, zonal flows and macroscopic flows, should interact with each other, and the mutual interactions should sustain the homeostasis of turbulent plasma and cause abrupt changes in the state. Macroscopic flows can be a cause of any structural bifurcation of a plasma, while cross-field transport should be determined at the level of microscopic drift-waves, which is regulated through nonlinear couplings with mesoscale zonal flows. Therefore, the key for a greater understanding is to investigate the genuine properties of the fundamental elements and the reality of their mutual interactions, called cross-scale couplings. Research along the above-mentioned view requires the quantification or visualization of mutual interactions between such disparate scale structure and fluctuations.

Several analysis methods have already been used for quantifying cross-scale couplings between the turbulence elements. Bicoherence is the one of such analysis methods used to quantify three-wave couplings in turbulence.⁷¹⁾ The definition of the bicoherence is   

\begin{equation*} b^{2}(\omega_{1},\omega_{2}) = \frac{|\langle\tilde{f}(\omega_{1})\tilde{f}(\omega_{2})\tilde{f}^{*}(\omega_{3})\rangle|^{2}}{\langle|\tilde{f}(\omega_{1})\tilde{f}(\omega_{2})|^{2}\rangle\langle|\tilde{f}(\omega_{3})|^{2}\rangle}, \end{equation*}

where $\tilde{f}(\omega_{1})$, $\tilde{f}(\omega_{2})$ and $\tilde{f}(\omega_{3})$ represent the Fourier coefficients at frequencies of ω₁, ω₂ and ω₃ (= ω₁ + ω₂), respectively. If the three waves are not coupled to give a random phase, the numerator should give a value close to zero. In contrast, the numerator should converge to a finite value if they are nonlinearly coupled.

Bicoherence analysis has proved the cross-scale couplings between microscale fluctuations and Geodesic Acoustic Modes (GAM), which is the oscillatory branch of zonal flows.^72)–75) A stellarator experiment, using a two-dimensional probe array, extended the bicoherence on the frequency to the wavenumber domain, and provided a complete demonstration that zonal flows should be generated from microscopic turbulence.⁷⁶⁾ Besides, in a cylindrical plasma in the Large Mirror Device (LMD), a cross-bicoherence analysis suggested the existence of the spatial transfer process of energy between the core and the edge through zonal flows coupled to local turbulence⁷⁷⁾; the zonal flows lose their energy at the edge, but gain energy in the core. Moreover, the cross-bicoherence analysis confirmed that a macroscopic fluctuating structure covering the entire plasma cross-section should be excited through nonlinear couplings with microscopic turbulence in a low-density Large Helical Device (LHD) plasma,⁷⁸⁾ which should cause long-distance couplings between local micro-fluctuations.

Multi-point measurements can provide indirect instances to display the importance of cross-scale couplings. The presence of cross-scale couplings should emerge in steady-state transport. Simultaneous measurements, using multi-channel probes in a cylindrical plasma of the Large Mirror Device Upgrade (LMD-U), showed a symmetric nature with a non-Gaussian statistical property of the turbulent Reynolds stress and turbulence-driven particle fluxes at individual measurement positions along the azimuthal direction. However, the azimuthally averaged fluxes were different from that of the individual distribution, indicating that they are globally correlated with each other.⁷⁹⁾ This observation is quite important concerning the point that suggests that a simple summation of turbulence-driven fluxes around the symmetric surface may not give a correct total flux induced by the turbulence owing to its global linkage, even if the plasma has a symmetric nature. Moreover, it suggests that a more complicated nature should be endowed with the turbulence fluxes in torus plasmas where an inherent asymmetric nature exists.

3.2. Reality of turbulence dynamics.

The turbulence cannot be stationary, but dynamic. The elemental fluctuations and structure of plasma turbulence, including the processes of their interactions, should have their own lifetimes. Consequently, a method is necessary to resolve the dynamic nature of turbulence. Their local measurement using the HIBPs in CHS succeeded in revealing the dynamic nature of the interactions between zonal flows and microscopic turbulence. For instance, the turbulence properties, including the couplings of zonal flows with background turbulence, should change according to the phase of the zonal flows, since the zonal flow timescale is one hundred-times slower than that of the background turbulence. Figure 5 shows an example of wavelet analysis concerning the mutual interactions between zonal flows and microscopic turbulence.⁸⁰⁾ It is found that the integrated fluctuation amplitude for the drift-wave frequencies (here, 30–100 kHz) should be modulated with the frequency of the zonal flows at 0.5 kHz. The conditional average confirms a clear difference, i.e., a fluctuation power of around ∼50 kHz is lower at the zonal flow maximum than that at the zonal flow minimum.

Fig. 5.

Mutual interaction between mesoscopic zonal flows and microscopic turbulence. (a) Quasi-energy conservation between zonal flows and microscopic turbulence. As the zonal flow’s fraction, q_ZF, increases, the turbulence fraction, q_turb, decreases with that of GAMs, q_GAM, being constant, where GAM is an oscillatory branch of zonal flows that correspond to the peak at ∼20 kHz in the power spectra ion the right-hand-side (or (c)). The relations q_turb ≃ 0.91 − q_ZF and q_GAM ≃ 0.09 have been found, and suggest the quasi-conservation of zonal flows, including GAM and turbulence, where GAM is the coherent oscillation indicated by the peak at ∼20 kHz in (c). (b) Temporal evolutions of microscopic turbulence and zonal flows. The blue dashed lines indicate the amplitude or the envelope of zonal flows. It is found that the turbulence power should be modulated with the phase of the zonal flows. (c) Conditional average of the turbulence power spectra for the minimum and maximum of zonal flows. In the minimum of zonal flows, the turbulence power is clearly increased. (d) Couplings strength quantified with wavelet bicoherence. In the minimum of zonal flows, the couplings between the zonal flows and the turbulence and those between the microscopic turbulence become significant in the frequency range of around ∼50 kHz.

Moreover, a wavelet bicoherence analysis^81),82) was applied to examine the behavior of the nonlinear coupling strength. The Fourier coefficient should be replaced by the Morlet’s wavelet coefficients in the formula of bicoherence, owing to its correspondence to the traditional Fourier spectral analysis. Again, the conditional average of the wavelet bicoherence was calculated for the maxima and minima of the zonal flows; the result showed that the couplings between the microscopic turbulence at around ∼50 kHz should also be enhanced (or suppressed) at a local minimum (or a local maximum) of the zonal flows, as well as the couplings between the zonal flows and the microscopic turbulence. The result showed the presence of phase-dependent couplings between the microscopic turbulence and the zonal flows. The local measurement cannot distinguish the reality of the theoretically predicted interactions, such as zonal flow shearing, wave-scatterings, wave-trappings and so on. Only an entire field observation can reveal their reality of the mutual interactions between the fundamental elements in a turbulent plasma unambiguously.

3.3. Flows and turbulence at barrier.

Not only mesoscale zonal flows, but also macroscopic flows, can be generated from microscopic turbulence nonlinearly through the Reynolds stress term of the Eulerian derivative. Being based on flow generation due to the turbulence, the so-called prey and predator model⁹⁾ was proposed to explain the H-mode transition. In this model, an increase in the turbulence (prey) should generate macroscopic flows (predator), while the generated flows should regulate or suppress the turbulence through their shearing effects on the turbulence. Simultaneous equations based on the nonlinear linkage between the flows and the turbulence can give two bifurcated states corresponding to the L- and H-modes. In addition to an experiment to confirm the capability of the Reynolds stress to drive macroscopic flows,⁸³⁾ direct experimental observations were also obtained to support the model,⁸⁴⁾ although the other experiments supported the standard Itoh’s scenario.⁸⁵⁾

On the other hand, the role of zonal flows on confinement was really confirmed in the transport barrier of a stellarator. For the transport barrier, a question that remains is why the transport is also improved inside the barrier, where no significant sheared flows exist. The HIBP measurement showed that the power of zonal flows inside the barrier clearly increased, while keeping the quasi-conservation of free energy transferred to the zonal flows and microscopic turbulence (c.f. Fig. 5(a)), with a decrease in the turbulence power. The reduction of turbulence energy contributes to the confinement improvement, since zonal flows cause no radial transport,^86),87) because the shearing effects of the zonal flows in CHS are too small to cause a visible reduction of the turbulence. These observations really confirmed that the zonal flows should be regarded as being another important ingredient for plasma confinement. Moreover, several experiments found the existence of intermediate states between the L- and H-modes, which were characterized by limit cycle oscillations caused by mutual interactions between the microscopic turbulence, zonal flows, and macroscopic flows,^88)–91) suggesting the participation of more complicated processes in the formation of a transport barrier.

3.4. Symmetry-breaking phenomenon — Streamers.

In turbulence plasmas a short-lived localized structure can emerge to break the symmetry, owing to nonlinearity. Streamers are one of such structures expected to emerge in linear and torus plasmas.^10),92),93) The streamers are radially elongated and poloidally (or azimuthally) localized structures born in turbulence, as is similar to zonal flows. In contrast to zonal flows, however, the streamers should degrade the confinement by enhancing the transport to connect the core and edge of plasmas. There were only a few experimental observations to suggest the signature of the streamers in toroidal plasma experiments.^94),95) On the other hand, the streamers were identified in a linear plasma,^96)–98) and stimulated investigations of the fundamental processes of the streamers formation.

The streamers were found in a linear plasma to be created through nonlinear couplings between modes called the carriers (drift-waves) and the mediator. Figure 6 shows the streamer structure of a radially elongated and azimuthally localized shape, which really induces ballistic transport to directly connect the plasma core to the edge on a one-order faster time scale than that of stationary turbulence. The other physically interesting aspect is that the envelope of the streamers and the mediator were found to have higher harmonic components generated by self-couplings. As shown in Fig. 6(c), both waveforms become more sharpened as their amplitude increases, demonstrating the characteristics of solitons.⁹⁷⁾ The presence of streamers should be pursued in toroidal plasmas in a future experiment that can catch the whole, at least two-dimensional, picture of the short-lived localized structure.

Fig. 6.

Streamers in a linear plasma. (a) Streamer structure measured using Langmuir probes. The structure is reconstructed with the conditional average of the deduced electron density from ion saturation current measurements. The density structure shows the property of streamers that are radially elongated and azimuthally localized. (b) Temporal evolution of the radial structure of the transport associated with streamers. The streamers emerge quasi-periodically to cause cross-field transport connecting the plasma core to the edge. (c) Soliton characteristics of the streamer envelope and the mediator. The sharpness represented by the parameter α increases with their amplitudes.

3.5. Global linkage and abrupt structural change.

An abrupt or discrete change is one of the unique features of a strongly nonlinear system in non-equilibrium.⁹⁹⁾ The entire structural changes of a plasma can be triggered with a symmetry-breaking phenomenon. A mysterious linkage between the core and the periphery of the plasmas has been reported concerning tokamaks and stellarators, including one observed in electric pulsation in CHS. The first observation was a simultaneous rise of the electron temperature at the plasma center when the edge plasma was cooled due to pellet injection in the TEXT-U tokamak.¹¹⁾ Similarly, the central temperature was observed to start rising immediately at the H-mode transition occurring at the edge in the JET tokamak.¹⁰⁰⁾ These mysterious linkages between the core and the edge have casted a question of how the local changes at sufficiently distant locations could occur simultaneously, or how the occurrence of a local event can propagate to other distant locations ballistically on a much faster time scale compared to the diffusive time scale (or confinement time scale).

Several experiments have suggested the importance of symmetry-breaking phenomena for abrupt changes of global structure. It has recently been found that the onsets of bursty phenomena should occur to begin at a local position; for example, the ELMs, sawtooth instability,¹⁰¹⁾ and the tongue instabilities in LHD most recently.¹⁰²⁾ The common feature for these phenomena is the occurrence of a local event to trigger abrupt and global changes of the structure. One of the possible candidates to explain the global change should be the cross-scale couplings between micro-scale turbulence and a longer scale of fluctuations or structures, e.g., mesoscale zonal flows and a larger structure coupled with smaller-scale fluctuations. The concepts of symmetry breaking and global linkage should be the keys to understand the underlying physics of the abrupt changes in the entire plasma structure.

4. Future prospects and conclusion

4.1. Prospects of plasma turbulence experiments.

The previous sections present the modern problems concerning plasma, such as mutual couplings between disparate scale fluctuations and structures, the mechanism of transport barrier formation, the identification of short-lived localized structures to break symmetry, abrupt changes of structure with global linkages, and so on. Moreover, in magnetic confinement fusion research, many unsolved problems associated with the origins of empirical scaling laws remain; the turbulence-related phenomena include the isotope effects, power degradation, and the confinement dependence on plasma shape. The reality of the plasma turbulence field should be examined to provide the underlying physics or to solve these unsolved issues.

To disclose the reality of the plasma turbulence field should require new advanced observations or diagnostics to catch the entire plasma at every scale of fluctuations and structure. To realize such advanced observations needs a new device and project where new advanced diagnostics, for example, tomography for plasma turbulence, can be realized,^103)–105) although a physics-oriented study might be possible concerning the present-day device relevant to ITER. Such a device, named PLAsma Turbulence Observatory (PLATO), is being constructed in a project entitled ‘Plasma Turbulence Observation System for puzzling out the principles of structural formation and functional expression in turbulent plasmas’ under the support of Specially Promoted Research,^104),105) with an aim to clarify any unsolved problems concerning the concept of symmetry-breaking and global linkage.

4.2. Tomography for entire plasma measurements.

Tomography is one of the possible diagnostics to measure the entire field of plasma turbulence. However, tomography has never been used to measure plasma turbulence, although it has provided a macroscopic structural evolution of plasma, such as sawtooth oscillations.^106),107) Prototypes of tomography were installed on a linear plasma device, Plasma Assembly for Nonlinear Turbulence Analysis (PANTA), to confirm the feasibility for its use in turbulence measurement.^108)–110) Prototypes are set on a specially-designed vacuum chamber, with the simultaneous detection of ArI and ArII emission, since the PANTA device usually produces argon plasmas. In this experiment, a temporal series of experimental sinograms (or a data set of line-integrated emissions), a huge amount of data (0.3 Gbyte) for a shot, can be converted into reconstructed images with parallel computing.¹¹¹⁾ Note that the data is usually sampled in 1 µs, for a duration approximately of 0.6 s.

The obtained line-integrated data is reconstructed to local emission by using an algorithm named Maximum Likely-Expectation Maximization (MLEM),¹¹²⁾ which has been developed for positron emission tomography (PET). This method was carefully chosen after trying various algorithms, such as Fourier-Zernike-Chebyshev (Cormack’s),¹¹³⁾ Fourier-Bessel function (FBF) series expansion,¹¹⁴⁾ and others.^115)–117) In the selection, those algorithms with a priori assumptions are avoided, for example, methods involving function fittings using Cormack’s and FBF series expansions. This is because the reconstruction algorithm for plasma tomography needs a capability to detect any abrupt or discrete change occuring spatiotemporally in turbulent plasmas owing to its strong nonlinearity.

Further, a number of methods have been developed to analyze tomography images; structural analyses based on Fourier-Bessel function expansion with optimizing a better set of the function bases,¹¹⁸⁾ Fourier-rectangular function expansion with an excellent property in local radial resolution by improving the Fourier-Bessel expansion,¹¹⁹⁾ and a concise and faster algorithm based on Tikhonov regulation to be used as a monitor between shots.¹²⁰⁾ Moreover, analyzing methods for dynamics have also been developed, such as a moment analysis to extract the global dynamic characteristics of a turbulence field¹⁰⁹⁾ and application of the Stokes parameters analysis in optics to detect rotation (or polarization) pattern.¹²¹⁾ Multi-color detection provides a possibility for the simultaneous evaluation of local fluctuations of the electron temperature and the density, which was recently confirmed in a comparison with a probe measurement.¹²²⁾ Finally, the tomography succeeded in measuring the plasma turbulence field, as shown in Fig. 7, to prove the feasibility that tomography can be used to measure plasma turbulence.

Fig. 7.

Results obtained in a prototype system of tomography to measure the plasma turbulence field. This system is installed on a linear plasma device, named PANTA. (a) Plasma images observed with ArI and ArII emissions. The left and right images were reconstructed using the MLEM method and those fitted with Fourier-Bessel functions to MLEM images. (b) Temporal evolution of the local emission of ArI and ArII. (c) Wavelet and Fourier spectra for ArI and ArII emission. The fluctuation power is significantly above the noise level. The result shows that the turbulence is well measured by tomography.

4.3. Concluding remarks.

This article describes discoveries and phenomena used to create an awareness of the presence of the mysterious nature and functions of a plasma turbulence field that generate ephemeral elements interacting with each other to sustain the homeostasis of plasma and to cause the entire structural bifurcation. The phenomena and problems provide common and universal physics that could serve for the understanding of other natural phenomena. Turbulence-driven transport could be related to the anomalous momentum transport observed in accretion disks around black holes, while transport barrier formation could be associated with the solar tachocline.¹²³⁾ Moreover, the Hasegawa-Mima-Charney equation has indicated the identity between drift-wave and Rossby wave turbulence. In other words, a direct analogue of zonal flows and fields should be valid concerning the physics describing the generation of atmosphere flows and magnetic fields associated with a rotating planet. Besides, turbulence plasma should provide common interests with many other phenomena, since the universe is full of both plasma and turbulence.

On the other hand, comprehending turbulent plasma would contribute to realizing an economic nuclear fusion reactor as one application. Although producing a burning plasma in ITER is approaching, the underlying physics for empirical confinement laws, which were used for its design, still remain unknown. These issues should be resolved by more fully understanding plasma turbulence. Moreover, efforts should still be needed in another direction: to search for a more sophisticated guiding principle of magnetic confinement configuration. The physics of turbulent plasmas makes it possible to design the optimized magnetic configuration in terms of turbulence, in analogy to a German stellarator device, Wendelstein 7-X,¹²⁴⁾ in which the magnetic-field configuration is optimized in terms of particle orbits. In addition, a physics-based understandings of whether it can give a complete prediction of plasma performance should dispense with expensive processes to construct a huge prototype device for a configuration study.

Finally, it should require a new physics experiment to pursue the ultimate principle of turbulent plasmas, simultaneously to help in the systematization of knowledge accumulated in past studies. A particular physics device is really required to be constructed for the future development of plasma physics, although physics experiments conducted in rather low-temperature devices have become a new international trend.^125)–128) The PLATO device, a tokamak with tomography, is constructed exactly for the purpose to realize measurements covering the entire field of plasma turbulence so as to pursue the reality of turbulent plasma. The research of turbulent plasma provides a new physics field for the 21st century, that is, as a representative system of far non-equilibrium and strong nonlinearity, as well as contributing to realizing an economic nuclear fusion reactor.

Acknowledgements

This paper is dedicated to Prof. S.-I. Itoh, who passed away in July of 2019, in a deep respect of her outstanding effort and distinguished achievements throughout her life, particularly her paving the way for a new recognition of plasma and turbulence. The author expresses his sincere appreciations to Prof. K. Itoh and Prof. K. Matsuoka for the long-term supports and encouragements. The appreciation is also given to members of Research Center for Plasma Turbulence for their cooperation. This work was partly supported by JSPS KAKENHI Grant Nos. JP23246162 and JP17H06089.

Notes

Edited by Atsuhiro NISHIDA, M.J.A.

Correspondence should be addressed: A. Fujisawa, Research Institute for Applied Mechanics, Kyushu University, 6-1 Kasuga Kouen, Kasuga, Fukuoka 816-8580, Japan (e-mail: [e-mail]).

References

• 1)   Mazzucato,  E. (1976) Small-scale density fluctuations in the adiabatic toroidal compressor. Phys. Rev. Lett. 36, 792–794.
• 2)   Surko,  C.M. and  Slusher,  R.E. (1976) Study of the density fluctuations in the adiabatic toroidal compressor tokamak using CO₂ laser. Phys. Rev. Lett. 37, 1747–1750.
• 3)   Hickok,  R.L. (1994) A short history of heavy ion beam probing. IEEE Trans. Plasma Sci. 22, 287–290.
• 4)   Fonck,  R.J. (1985) Charge exchange recombination spectroscopy as a plasma diagnostic tool. Rev. Sci. Instrum. 56, 885–890.
• 5)   Wagner,  F.,  Becker,  G.,  Behringer,  K.,  Campbell,  D.,  Eberhagen,  A.,  Engelhardt,  W. (1982) Regime of improved confinement and high beta in neutral-beam-heated divertor discharge of the ASDEX tokamak. Phys. Rev. Lett. 49, 1408–1412.
• 6)   Itoh,  S.-I. and  Itoh,  K. (1988) Model of L to H-mode transition in tokamak. Phys. Rev. Lett. 60, 2276–2279.
• 7)   Fujisawa,  A.,  Itoh,  K.,  Iguchi,  H.,  Matsuoka,  K.,  Okamura,  S.,  Shimizu,  A. (2004) Identification of zonal flows in a toroidal plasma. Phys. Rev. Lett. 93, 165002.
• 8)   Fujisawa,  A.,  Itoh,  K.,  Shimizu,  A.,  Nakano,  H.,  Ohshima,  S.,  Iguchi,  H. (2007) Experimental evidence of a zonal magnetic field in a toroidal plasma. Phys. Rev. Lett. 98, 165001.
• 9)   Diamond,  P.H.,  Liang,  Y.-M.,  Carreras,  B.A. and  Terry,  P.W. (1994) Self-regulating shear flow turbulence: A paradigm for the L to H transition. Phys. Rev. Lett. 72, 2565–2568.
• 10)   Diamond,  P.H.,  Champeaux,  S.,  Malkov,  M.,  Das,  A.,  Gruzinov,  I.,  Rosenbluth,  M.N. (2001) Secondary instability in drift wave turbulence as a mechanism for zonal flow and avalanche formation. Nucl. Fusion 41, 1067–1080.
• 11)   Gentle,  K.W.,  Rowa,  W.L.,  Bravenec,  R.V.,  Cima,  G.,  Crowley,  T.P.,  Gasquet,  H. (1995) Strong nonlocal effects in a tokamak perturbative transport experiment. Phys. Rev. Lett. 74, 3620–3623.
• 12)   Liewer,  P.C. (1985) Measurements of microturbulence in tokamaks and comparisons with theories of turbulence and anomalous transport. Nucl. Fusion 25, 543–621.
• 13)   Wootton,  A.J.,  Carreras,  B.A.,  Matsumoto,  H.,  McGuire,  K.,  Peebles,  W.A.,  Ritz,  Ch.P. (1990) Fluctuations and anomalous transport in tokamaks. Phys. Fluids B 2, 2879–2903.
• 14)   Tynan,  G.R.,  Fujisawa,  A. and  McKee,  G. (2009) A review of experimental drift turbulence studies. Plasma Phys. Contr. Fusion 51, 113001.
• 15)   Surko,  C. and  Slusher,  R.E. (1983) Waves and turbulence in a tokamak fusion plasma. Science 221, 817–822.
• 16)  TFR group (1986) Correlation between low frequency turbulence and energy confinement in TFR. Nucl. Fusion 26, 1303–1310.
• 17)   Kadmotsev,  B.B. and  Pogutse,  O.P. (1971) Trapped particles in toroidal magnetic systems. Nucl. Fusion 11, 67–92.
• 18)   Horton,  W. and  Varma,  R.K. (1972) Electrostatic stability theory of tokamaks from two-component fluid equations. Phys. Fluids 15, 620–631.
• 19)   Brower,  D.L.,  Peebles,  W.A.,  Luhmann,  N.C. Jr. and  Savage,  R.L. Jr. (1985) Multichannel scattering studies of the spectra and spatial distribution of tokamak microturbulence. Phys. Rev. Lett. 54, 689–692.
• 20)   Hallock,  G.A.,  Wootton,  A.J.,  Hickok,  R.L. and  Isler,  R.C. (1987) Space-potential and density fluctuations in the ISX-B tokamak. Phys. Rev. Lett. 59, 1301–1304.
• 21)   Ritz,  Ch.P.,  Bravenec,  R.V.,  Schoch,  P.M.,  Bengston,  R.D.,  Boedo,  J.A.,  Forster,  J.C. (1989) Fluctuation-induced energy flux in the tokamak edge. Phys. Rev. Lett. 62, 1844–1847.
• 22)   Todd,  A.M.M.,  Chance,  M.S.,  Greene,  J.M.,  Grimm,  R.C.,  Johnson,  J.L.,  Manickam,  J. (1977) Stability limitations on high-beta tokamaks. Phys. Rev. Lett. 38, 826–829.
• 23)   Watts,  C.,  Gandy,  R.F. and  Cima,  G. (1996) Evidence for poloidal asymmetry of core electron temperature fluctuations in the Texas experimental tokamak. Phys. Rev. Lett. 76, 2274–2277.
• 24)   Fujisawa,  A.,  Ouroua,  A.,  Heard,  J.W.,  Crowley,  T.P.,  Schoch,  P.M.,  Connor,  K.A. (1996) Ballooning characteristics in density fluctuations observed with the 2 MeV heavy ion beam probe on the TEXT-U tokamak. Nucl. Fusion 36, 375–379.
• 25)   Birkenmeier,  G.,  Ramisch,  M.,  Manz,  P.,  Nold,  B. and  Stroth,  U. (2011) Experimental investigation of the magnetic configuration dependence of turbulent transport. Phys. Rev. Lett. 107, 025001.
• 26)  Pfirsch, D. and Schlüter, A. (1962) Der Einfluß der Elektrischen Leitfähigkeit auf das Gleichgewichtsverhalten von Plasmen Niedrigen Drucks in Stellaratoren. Max-Planck-Institut für Physik und Astrophysik, Munich, Report No. MPI/PA/7/62.
• 27)   Stringer,  T.E. (1969) Diffusion in toroidal plasmas with radial electric field. Phys. Rev. Lett. 22, 770–774.
• 28)   Hassam,  A.B.,  Antonsen,  T.M. Jr.,  Drake,  J.F. and  Liu,  C.S. (1991) Spontaneous poloidal spin-up of tokamaks and the transition to the H mode. Phys. Rev. Lett. 66, 309–312.
• 29)   Wagner,  F. (2007) A quarter-century of H-mode studies. Plasma Phys. Contr. Fusion 49, B1–B33.
• 30)   Fujisawa,  A. (2003) Experimental studies of structural bifurcation in stellarator plasmas. Plasma Phys. Contr. Fusion 45, R1–R88.
• 31)   Strachan,  J.D.,  Bitter,  M.,  Ramsey,  A.T.,  Zarnstorff,  M.C.,  Arunasalam,  V.,  Bell,  M.G. (1987) High-temperature plasmas in a tokamak fusion test reactor. Phys. Rev. Lett. 58, 1004–1007.
• 32)   Koide,  Y.,  Kikuchi,  M.,  Mori,  M.,  Tsuji,  S.,  Ishida,  S.,  Asakura,  N. (1994) Internal transport barrier on q = 3 surface and poloidal plasma spin up in JT-60U high-β_p discharges. Phys. Rev. Lett. 72, 3662–3665.
• 33)   Levinton,  F.M.,  Zarnstorff,  M.C.,  Batha,  S.H.,  Bell,  M.,  Budny,  R.V.,  Bush,  C. (1995) Improved confinement with reversed magnetic shear in TFTR. Phys. Rev. Lett. 75, 4417–4420.
• 34)   Strait,  E.J.,  Lao,  L.L.,  Mauel,  M.E.,  Rice,  B.W.,  Taylor,  T.S.,  Burrell,  K.H. (1995) Improved confinement with reversed magnetic shear in TFTR. Phys. Rev. Lett. 75, 4421–4424.
• 35)   Fujisawa,  A.,  Iguchi,  H.,  Minami,  T.,  Yoshimura,  Y.,  Sanuki,  H.,  Itoh,  K. (1999) Electron thermal transport barrier and density fluctuation reduction in a toroidal helical plasma. Phys. Rev. Lett. 82, 2669–2672.
• 36)   Stroth,  U.,  Itoh,  K.,  Itoh,  S.-I.,  Hartfuss,  H.,  Laqua,  H., the ECRH team (2001) Internal transport barrier triggered by neoclassical transport in W7-AS. Phys. Rev. Lett. 86, 5910–5913.
• 37)   Alejaldre,  C.,  Almoguera,  L.,  Alonso,  J.,  Ascasíbar,  E.,  Baciero,  A.,  Balbín,  R. (2001) Review of confinement and transport studies in the TJ-II flexible heliac. Nucl. Fusion 41, 1449–1457.
• 38)   Ida,  K. and  Fujita,  T. (2018) Internal transport barrier in tokamak and helical plasmas. Plasma Phys. Contr. Fusion 60, 033001.
• 39)   Messiaen,  A.M.,  Ongena,  J.,  Samm,  U.,  Unterberg,  B.,  Van Wassenhove,  G.,  Durodie,  F. (1996) High confinement and high density with stationary plasma energy and strong edge radiation in the TEXTOR-94 tokamak. Phys. Rev. Lett. 77, 2487–2490.
• 40)   McCormick,  K.,  Grigull,  P.,  Burhenn,  R.,  Brakel,  R.,  Ehmler,  H.,  Feng,  Y. (2002) New advanced operational regime on the W7-AS stellarator. Phys. Rev. Lett. 89, 015001.
• 41)   Shaing,  K.C. and  Crume,  E. Jr. (1989) Bifurcation theory of poloidal rotation in tokamaks: A model for L-H transition. Phys. Rev. Lett. 63, 2369–2372.
• 42)   Itoh,  K. and  Itoh,  S.-I. (1996) The role of the electric field in confinement. Plasma Phys. Contr. Fusion 38, 1–49.
• 43)   Shaing,  K.C.,  Hazeltine,  R.D. and  Sanuki,  H. (1992) Shock formation in a poloidally rotating tokamak plasma. Phys. Fluids B 4, 404–412.
• 44)   Biglari,  H.,  Diamond,  P.H. and  Terry,  P.W. (1990) Influence of sheared poloidal rotation on edge turbulence. Phys. Fluids B 2, 1–3.
• 45)  Shaing, K.C., Lee, G.S., Carreras, B.A., Houlberg, W.A. and Crume, E.C., Jr. (1989) Model for the L-H transition in tokamaks. In Proceedings of 12th International Conference on Plasma Physics and Controlled Nuclear Fusion Research (Nice, 1988). International Atomic Energy Agency, Vienna, Vol. 2, pp. 13–22.
• 46)   Itoh,  K.,  Itoh,  S.-I.,  Fukuyama,  A.,  Sanuki,  H. and  Yagi,  M. (1994) Confinement improvement in H-mode-like plasmas in helical systems. Plasma Phys. Contr. Fusion 36, 123–130.
• 47)   Taylor,  R.J.,  Brown,  M.L.,  Fried,  B.D.,  Grote,  H.,  Liberati,  J.R.,  Morales,  G.J. (1989) H-mode behavior induced by cross-field currents in a tokamak. Phys. Rev. Lett. 63, 2365–2368.
• 48)   Weynants,  R.R.,  Van Oost,  G.,  Bertschinger,  G.,  Boedo,  J.,  Brys,  P.,  Delvigne,  T. (1992) Confinement and profile changes induced by the presence of positive or negative radial electric fields in the edge of the TEXTOR tokamak. Nucl. Fusion 32, 837–854.
• 49)   Weynants,  R.R.,  Jachmich,  S. and  Van Oost,  G. (1998) Demonstration of the role of ExB flow shear in improved confinement. Plasma Phys. Contr. Fusion 40, 635–639.
• 50)   Groebner,  R.J.,  Burrel,  K.H. and  Seraydarian,  R.P. (1990) Role of edge electric field and poloidal rotation in the L-H transition. Phys. Rev. Lett. 64, 3015–3018.
• 51)   Ida,  K.,  Hidekuma,  S.,  Miura,  Y.,  Fujita,  T.,  Mori,  M.,  Hoshino,  K. (1990) Edge electric-field profiles of H-mode plasmas in the JFT-2M tokamak. Phys. Rev. Lett. 65, 1364–1367.
• 52)   Fujisawa,  A.,  Iguchi,  H.,  Sasao,  M.,  Hamada,  Y. and  Fujita,  J. (1992) Active control of beam trajectories for heavy ion beam probe on helical magnetic configurations. Rev. Sci. Instrum. 63, 3694–3700.
• 53)   Fujisawa,  A.,  Iguchi,  H.,  Lee,  S.,  Crowley,  T.P.,  Hamada,  Y.,  Hidekuma,  S. (1996) Active trajectory control for a heavy ion beam probe on the compact helical system. Rev. Sci. Instrum. 67, 3099–3106.
• 54)   Fujisawa,  A.,  Iguchi,  H.,  Sanuki,  H.,  Itoh,  K.,  Lee,  S.,  Hamada,  Y. (1997) Dynamic behavior of potential in the plasma core of the CHS heliotron/torsatron. Phys. Rev. Lett. 79, 1054–1057.
• 55)   Fujisawa,  A.,  Iguchi,  H.,  Minami,  T.,  Yoshimura,  Y.,  Tanaka,  K.,  Itoh,  K. (2000) Experimental study of the bifurcation nature of the electrostatic potential of a toroidal helical plasma. Phys. Plasmas 7, 4152–4183.
• 56)   Fujisawa,  A.,  Shimizu,  A.,  Nakano,  H.,  Ohsima,  S.,  Itoh,  K.,  Iguchi,  H. (2006) Turbulence and transport characteristics of a barrier in a toroidal plasma. Plasma Phys. Contr. Fusion 48, S205–S212.
• 57)   Kovrizhnykh,  L.M. (1984) The energy confinement time in stellarators. Nucl. Fusion 24, 435–444.
• 58)   Hastings,  D.E. (1984) Neoclassical transport associated with collisionless detrapping in a bumpy torus. Phys. Fluids 27, 935–938.
• 59)   Itoh,  S.-I.,  Itoh,  K.,  Fukuyama,  A. and  Miura,  Y. (1991) Edge localized mode activity as a limit cycle in tokamak plasmas. Phys. Rev. Lett. 67, 2485–2488.
• 60)   Zohm,  H. (1994) Dynamic behavior of the L-H transition. Phys. Rev. Lett. 72, 222–225.
• 61)   Fujisawa,  A.,  Iguchi,  H.,  Idei,  H.,  Kubo,  S.,  Matsuoka,  K.,  Okamura,  S. (1998) Discovery of electric pulsation in a toroidal helical plasma. Phys. Rev. Lett. 81, 2256–2259.
• 62)   Glanz,  J. (1996) Turbulence may sink titanic reactor. Science 274, 1600.
• 63)   Rosenbluth,  M.N. and  Hinton,  F.L. (1998) Poloidal flow driven by ion-temperature-gradient turbulence in tokamaks. Phys. Rev. Lett. 80, 724–727.
• 64)   Diamond,  P.H.,  Itoh,  S.-I.,  Itoh,  K. and  Hahm,  T.S. (2005) Zonal flows in plasma — A review. Plasma Phys. Contr. Fusion 47, R35–R161.
• 65)   Fujisawa,  A. (2009) A review of zonal flow experiments. Nucl. Fusion 49, 013001.
• 66)   Hasegawa,  A. and  Mima,  K. (1977) Stationary spectrum of strong turbulence in magnetized nonuniform plasma. Phys. Rev. Lett. 39, 205–208.
• 67)   Williams,  G.P. (1978) Planetary circulations: 1. Barotropic representation of jovian and terrestrial turbulence. J. Atmos. Sci. 35, 1399–1426.
• 68)   Gruzinov,  I.,  Das,  A.,  Diamond,  P.H. and  Smolyakov,  A. (2002) Fast zonal field dynamo in collisionless kinetic Alfven wave turbulence. Phys. Lett. A 302, 119–124.
• 69)   Guzdar,  P.N.,  Kleva,  R.G.,  Das,  A. and  Kaw,  P.K. (2001) Zonal flow and zonal magnetic field generation by finite β drift waves: A theory for low to high transitions in tokamaks. Phys. Rev. Lett. 87, 015001.
• 70)   Fujisawa,  A.,  Shimizu,  A.,  Nakano,  H. and  Ohshima,  S. (2007) Evaluation of local magnetic field fluctuation in a toroidal plasma with heavy ion beam probe. Plasma Phys. Contr. Fusion 49, 845–855.
• 71)   Hidalgo,  C.,  Sánchez,  E.,  Estrada,  T.,  Brãnas,  B.,  Ritz,  Ch.P.,  Uckan,  T. (1993) Experimental evidence of three-wave coupling on plasma turbulence. Phys. Rev. Lett. 71, 3127–3130.
• 72)   Shats,  M.G.,  Solomon,  W.M. and  Xia,  H. (2003) Turbulent transport reduction and randomization of coherent fluctuations by zonal flows in toroidal plasma. Phys. Rev. Lett. 90, 125002.
• 73)   Nagashima,  Y.,  Hoshino,  K.,  Ejiri,  A.,  Shinohara,  K.,  Takase,  Y.,  Tsuzuki,  K. (2005) Observation of nonlinear coupling between small-poloidal wave-number potential fluctuations and turbulent potential fluctuations in ohmically heated plasmas in the JFT-2M tokamak. Phys. Rev. Lett. 95, 095002.
• 74)   Ido,  T.,  Miura,  Y.,  Hoshino,  K.,  Kamiya,  K.,  Hamada,  Y.,  Nishizawa,  A. (2006) Observation of the interaction between the geodesic acoustic mode and ambient fluctuation in the JFT-2M tokamak. Nucl. Fusion 46, 512–515.
• 75)   Zhao,  K.J.,  Lan,  T.,  Dong,  J.Q.,  Yan,  L.W.,  Hong,  W.Y.,  Yu,  C.X. (2006) Toroidal symmetry of the geodesic acoustic mode zonal flow in a tokamak plasma. Phys. Rev. Lett. 96, 255004.
• 76)   Manz,  P.,  Ramisch,  M. and  Stroth,  U. (2009) Physical mechanism behind zonal-flow generation in drift-wave turbulence. Phys. Rev. Lett. 103, 165004.
• 77)   Nagashima,  Y.,  Itoh,  S.-I.,  Shinohara,  S.,  Fukao,  M.,  Fujisawa,  A.,  Terasaka,  K. (2009) Observation of the parametric-modulational instability between the drift-wave fluctuation and azimuthally symmetric sheared radial electric field oscillation in a cylindrical laboratory plasma. Phys. Plasmas 16, 020706.
• 78)   Inagaki,  S.,  Tokuzawa,  T.,  Itoh,  K.,  Ida,  K.,  Itoh,  S.-I.,  Tamura,  N. (2011) Observation of long-distance radial correlation in toroidal plasma turbulence. Phys. Rev. Lett. 107, 115001.
• 79)   Nagashima,  Y.,  Itoh,  S.-I.,  Inagaki,  S.,  Arakawa,  H.,  Kasuya,  N.,  Fujisawa,  A. (2011) Non-Gaussian properties of global momentum and particle fluxes in a cylindrical laboratory plasma. Phys. Plasmas 18, 070701.
• 80)   Fujisawa,  A.,  Shimizu,  A.,  Nakano,  H.,  Ohshima,  S.,  Itoh,  K.,  Nagashima,  Y. (2007) Causal relationship between zonal flow and turbulence in a toroidal plasm. J. Phys. Soc. Jpn. 76, 033501.
• 81)   van Milligen,  B.Ph.,  Hidalgo,  C. and  Sánchez,  E. (1995) Nonlinear phenomena and intermittency in plasma turbulence. Phys. Rev. Lett. 74, 395–398.
• 82)   Fujisawa,  A.,  Shimizu,  A.,  Nakano,  H.,  Ohshima,  S.,  Itoh,  K.,  Nagashima,  Y. (2007) Intermittent characteristics in coupling between turbulence and zonal flows. Plasma Phys. Contr. Fusion 49, 211–217.
• 83)   Hidalgo,  C.,  Silva,  C.,  Pedrosa,  M.A.,  Sánchez,  E.,  Fernandes,  H. and  Varandas,  C.A.F. (1999) Radial structure of Reynolds stress in the plasma boundary of tokamak plasmas. Phys. Rev. Lett. 83, 2203–2206.
• 84)   Xu,  Y.H.,  Yu,  C.H.,  Luo,  J.R.,  Mao,  J.S.,  Liu,  B.H.,  Li,  J.G. (2000) Role of Reynolds stress-induced poloidal flow in triggering the transition to improved ohmic confinement on the HT-6M tokamak. Phys. Rev. Lett. 84, 3867–3870.
• 85)   Ido,  T.,  Kamiya,  K.,  Miura,  Y.,  Hamada,  Y.,  Nishizawa,  A. and  Kawasumi,  Y. (2002) Observation of the fast potential change at L-H transition by a heavy-ion-beam probe on JFT-2M. Phys. Rev. Lett. 88, 055006.
• 86)   Itoh,  K.,  Toda,  S. and  Fujisawa,  A. (2007) Physics of internal transport barrier of toroidal helical plasmas. Phys. Plasmas 14, 020702.
• 87)   Fujisawa,  A.,  Itoh,  K.,  Shimizu,  A.,  Nakano,  H.,  Ohshima,  S.,  Iguchi,  H. (2008) Experimental studies of zonal flow and field in compact helical system plasma. Phys. Plasmas 15, 055906.
• 88)   Conway,  G.D.,  Angioni,  C.,  Ryter,  F.,  Sauter,  P. and  Vicente,  J. (ASDEX Upgrade Team) (2011) Mean and oscillating plasma flows and turbulence interactions across the L-H confinement transition. Phys. Rev. Lett. 106, 065001.
• 89)   Estrada,  T.,  Hidalgo,  C.,  Happel,  T. and  Diamond,  P.H. (2011) Spatiotemporal structure of the interaction between turbulence and flows at the L-H transition in a toroidal plasma. Phys. Rev. Lett. 107, 245004.
• 90)   Cheng,  J.,  Dong,  J.Q.,  Itoh,  K.,  Yan,  L.W.,  Xu,  M.,  Zhao,  K.J. (2013) Dynamics of low-intermediate-high-confinement transition in toroidal plasmas. Phys. Rev. Lett. 110, 265002.
• 91)   Kobayashi,  T.,  Itoh,  K.,  Ido,  T.,  Kamiya,  K.,  Itoh,  S.-I.,  Miura,  Y. (2013) Spatiotemporal structures of edge limit-cycle oscillation before L-to-H transition in the JFT-2M tokamak. Phys. Rev. Lett. 111, 035002.
• 92)   Nozaki,  K.,  Taniuti,  T. and  Watanabe,  K.J. (1979) Solitons in a convective motion of a low-β plasma. II. Phys. Soc. Jpn. 46, 991–1001.
• 93)   Beyer,  P.,  Benkadda,  S.,  Barbet,  X. and  Diamond,  P.H. (2000) Nondiffusive transport in tokamaks: Three-dimensional structure of bursts and the role of zonal flows. Phys. Rev. Lett. 85, 4892–4895.
• 94)   Politzer,  P.A. (2000) Observation of avalanchelike phenomena in a magnetically confined plasma. Phys. Rev. Lett. 84, 1192–1195.
• 95)   Hamada,  Y.,  Watari,  T.,  Nishizawa,  A.,  Narihara,  K.,  Kawasumi,  Y.,  Ido,  T. (2006) Streamers in the JIPP T-llU tokamak plasmas. Phys. Rev. Lett. 96, 115003.
• 96)   Yamada,  T.,  Itoh,  S.-I.,  Maruta,  T.,  Kasuya,  N.,  Nagashima,  Y.,  Shinohara,  S. (2008) Anatomy of plasma turbulence. Nat. Phys. 4, 721–725.
• 97)   Kin,  F.,  Itoh,  K.,  Fujisawa,  A.,  Kosuga,  Y.,  Sasaki,  M.,  Yamada,  T. (2018) Extraction of nonlinear waveform in turbulent plasma. Phys. Plasmas 25, 062304.
• 98)   Kin,  F.,  Fujisawa,  A.,  Itoh,  K.,  Kosuga,  Y.,  Sasaki,  M.,  Inagaki,  S. (2019) Observations of radially elongated particle flux induced by streamer in a linear magnetized plasma. Phys. Plasmas 26, 042306.
• 99)   Itoh,  S.-I.,  Itoh,  K.,  Zushi,  H. and  Fukuyama,  A. (1998) Physics of collapse events in toroidal plasmas. Plasma Phys. Contr. Fusion 40, 879–930.
• 100)   Cordey,  J.G.,  Balet,  B.,  Barlett,  D.V.,  Budny,  R.V.,  Christiansen,  J.P.,  Conway,  G.D. (1999) Plasma confinement in JET H mode plasmas with H, D, DT and T isotopes. Nucl. Fusion 39, 301–308.
• 101)   Yun,  G.S.,  Lee,  W.,  Choi,  J.J.,  Park,  H.K.,  Tobias,  B.,  Domier,  C.W. (2011) Two-dimensional visualization of growth and burst of the edge-localized filaments in KSTAR H-mode plasmas. Phys. Rev. Lett. 107, 045004.
• 102)   Ida,  K.,  Kobayashi,  T.,  Itoh,  K.,  Yoshinuma,  M.,  Tokuzawa,  T.,  Akiyama,  T. (2016) Abrupt onset of tongue deformation and phase space response of ions in magnetically-confined plasmas. Sci. Rep. 6, 36217.
• 103)   Matsuoka,  K. (2011) Design of toroidal machine for plasma-turbulence research. Rep. RIAM Kyushu Univ. 141, 51–85.
• 104)   Itoh,  K.,  Itoh,  S.-I.,  Nagashima,  Y.,  Yamada,  Y.,  Kosuga,  Y. and  Fujisawa,  A. (2018) Symmetry-breaking of turbulence structure and position identification in toroidal plasmas. Plasma Fus. Res. 13, 1102113.
• 105)   Fujisawa,  A. (2018) Past and present experiments toward PLATO project. AIP Conf. Proc. 1993, 020010.
• 106)   Nagayama,  Y.,  Tsuji,  S. and  Kawahata,  K. (1988) Soft-x-ray tomography of sawtooth oscillations in the JIPP T-II tokamak. Phys. Rev. Lett. 61, 1839–1842.
• 107)   Park,  H.K.,  Donné,  A.J.H.,  Luhmann,  N.C. Jr.,  Classen,  I.G.J.,  Domier,  C.W.,  Mazzucato,  E. (2006) Comparison study of 2D images of temperature fluctuations during sawtooth oscillation with theoretical models. Phys. Rev. Lett. 96, 195004.
• 108)   Fujisawa,  A.,  Nagashima,  Y. and  Inagaki,  S. (2015) Tomography for local plasma turbulence measurements. Plasma Fus. Res. 10, 1201080.
• 109)   Fujisawa,  A.,  Nagashima,  Y.,  Inagaki,  S.,  Onchi,  T.,  Ohshima,  S. and  Shimizu,  A. (2016) Tomography as a promising diagnostic tool for plasma turbulence. Plasma Phys. Contr. Fusion 58, 025005.
• 110)   Yamasaki,  K.,  Fujisawa,  A.,  Nagashima,  Y.,  Moon,  C.,  Inagaki,  S. and  Yamada,  T. (2020) Tomography system for two-dimensional observation of fluctuation in magnetized plasma. Rev. Sci. Instrum. 91, 033502.
• 111)   Fujisawa,  A.,  Shimizu,  A.,  Itoh,  K.,  Nagashima,  Y.,  Yamada,  T.,  Inagaki,  S. (2010) Wavelet analyses using parallel computing for plasma turbulence studies. Phys. Plasmas 17, 104503.
• 112)   Shepp,  L.A. and  Vardi,  Y. (1982) Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imaging 1, 113–122.
• 113)   Cormack,  A.M. (1964) Representation of a function by its line integrals, with some radiological applications. II. J. Appl. Phys. 35, 2908–2912.
• 114)   Nagayama,  Y. (1987) Tomography of m = 1 mode structure in tokamak plasma using least-square-fitting method and Fourier-Bessel expansions. J. Appl. Phys. 62, 2702–2706.
• 115)  Natterer, F. (1986) The Mathematics of Computerized Tomography. Wiley, Philadelphia.
• 116)   Ramachandran,  G.N. and  Lakshminarayanan,  A.V. (1971) Three-dimensional reconstruction from radiographs and electron micrographs: Application of convolutions instead of Fourier transforms. Proc. Natl. Acad. Sci. U.S.A. 68, 2236–2240.
• 117)   Nardone,  C. (1992) Multichannel fluctuation data analysis by the singular value decomposition method. Application to MHD modes in JET. Plasma Phys. Contr. Fusion 34, 1447–1466.
• 118)   Yamasaki,  K.,  Fujisawa,  A. and  Nagashima,  Y. (2017) A proposal of Fourier-Bessel expansion with optimized ensembles of bases to analyse two dimensional image. Rev. Sci. Instrum. 88, 093507.
• 119)   Yamasaki,  K.,  Fujisawa,  A.,  Nagashima,  Y.,  Moon,  C.,  Inagaki,  S.,  Kasuya,  N. (2019) Fourier-rectangular function analysis for cylindrical plasma images. J. Appl. Phys. 126, 043304.
• 120)   Yamasaki,  K.,  Fujisawa,  A.,  Nagashima,  Y. and  Inagaki,  S. (2017) Fast algorithm for tomographic reconstruction for plasma emission. Plasma Fus. Res. 12, 1201045.
• 121)   Fujisawa,  A.,  Nagashima,  Y.,  Yamasaki,  K.,  Inagaki,  S.,  Yamada,  T. and  Sasaki,  M. (2019) Combined methods of moment vectors and Stokes parameters to analyze tomographic image of plasma turbulence. Phys. Plasmas 26, 012305.
• 122)   Nagashima,  Y.,  Fujisawa,  A.,  Yamasaki,  K.,  Inagaki,  S.,  Moon,  C.,  Kin,  F. (2020) Comparison between tomography and Langmuir probe data in PANTA. J. Phys. Soc. Jpn. 89, 093501.
• 123)   Charbonneau,  P.,  Christensen-Dalsgaard,  J.,  Henning,  R.,  Larsen,  R.M.,  Schou,  J.,  Thompson,  M.J. (1999) Helioseismic constraints on the structure of the solar tachocline. Astrophys. J. 527, 445–460.
• 124)   Klinger,  T.,  Andreeva,  T.,  Bozhenkov,  S.,  Brandt,  C.,  Burhenn,  R.,  Buttenschön,  B. (2019) Overview of first Wendelstein 7-X high-performance operation. Nucl. Fusion 59, 112004.
• 125)   Hong,  R.,  Li,  J.C.,  Chakraborty Thakur,  S.,  Hajjar,  R.,  Diamond,  P.H. and  Tynan,  G.R. (2018) Tracing the pathway from drift-wave turbulence with broken symmetry to the production of sheared axial mean flow. Phys. Rev. Lett. 120, 205001.
• 126)   Gekelman,  W.,  Pribyl,  P.,  Lucky,  Z.,  Drandell,  M.,  Leneman,  D.,  Maggs,  J. (2016) The upgraded large plasma device, a machine for studying frontier basic plasma physics. Rev. Sci. Instrum. 87, 025105.
• 127)   Schmid,  B.,  Manz,  P.,  Ramisch,  M. and  Stroth,  U. (2017) Collisional scaling of the energy transfer in drift-wave zonal flow turbulence. Phys. Rev. Lett. 118, 055001.
• 128)   Gonzalez-Fernandez,  V.,  David,  P.,  Baude,  R.,  Escarguel,  A. and  Camenen,  Y. (2020) Spatially resolved determination of the electronic density and temperature by a visible spectro-tomography diagnostic in a linear magnetized plasma. Sci. Rep. 10, 5389.

Profile

Akihide Fujisawa was born in Hokkaido prefecture in 1961 and graduated from the University of Tokyo in 1985. After receiving his Ph.D. degree from the University of Tokyo in 1990, he started to work at National Institute for Fusion Science. He joined a stellarator experiment, and took charge of a plasma diagnostic project named heavy ion beam probe (HIBP). HIBP is a quite powerful tool to detect the plasma density, potential, magnetic field and their fluctuations simultaneously. The developed HIBPs resulted in many discoveries, such as the bifurcation of electric fields in torus plasma, the oscillatory state associated with bifurcation, an internal transport barrier in a stellarator as well as zonal flows and zonal magnetic fields. After these achievements, he moved to Kyushu University in 2009. He then started a new project aimed at plasma turbulence research, and has recently completed the construction of a new-age machine for plasma turbulence experiments. For these accomplishments, he received several prizes including the Inoue Prize for Science (2009), Commendation for Science and Technology from the Japanese Minister of Education Culture, Sports, Science and Technology (2010). He then received the Nishina Memorial Prize (2011) and an outstanding paper award from the Physical Society of Japan (2012).