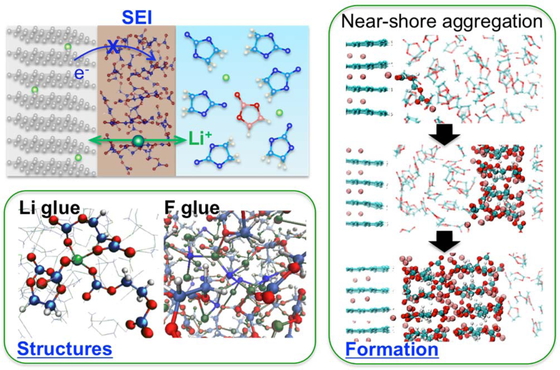
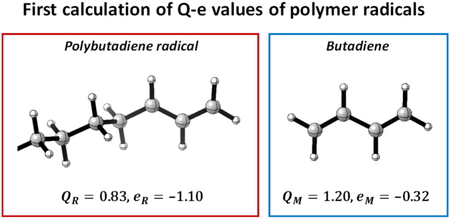
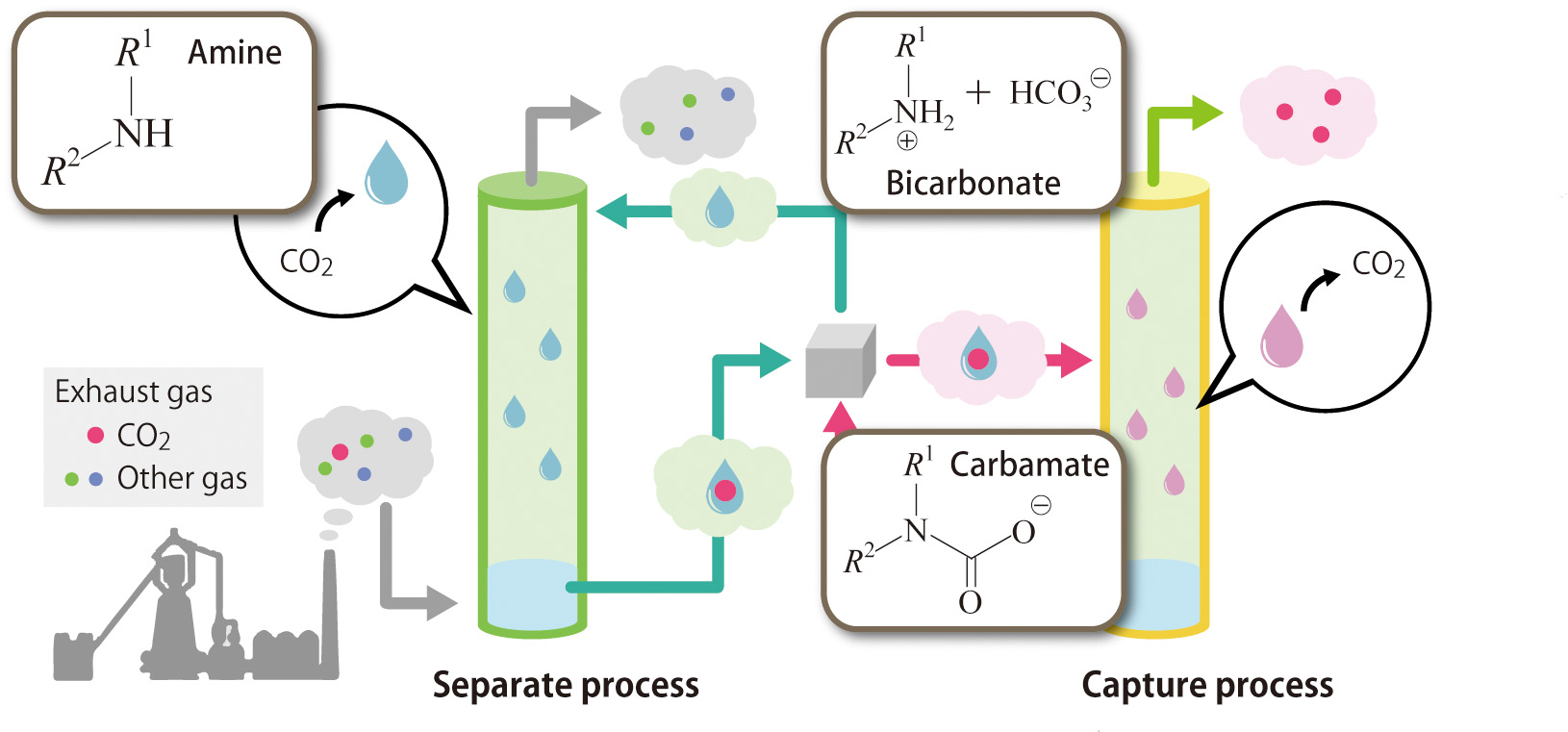
Journal of Computer Chemistry, Japan

Journal of Computer Chemistry, Japan

Published by Society of Computer Chemistry, Japan

1,124 registered articles
(updated on March 08, 2026)

Online ISSN : 1347-3824
Print ISSN : 1347-1767
ISSN-L : 1347-1767

JOURNAL PEER REVIEWED FREE ACCESS FULL-TEXT HTML ADVANCE PUBLICATION
J-STAGE Data

2025 Volume 24 Issue 3

[title in Japanese] [in Japanese]
Molecular Dynamics Simulation Analysis of Structural Changes and Fluctuations in Taste Receptor Protein-Amino Acid Ligand Complexes Kie ARAKI, Koji ANDO
Singular Spectrum Analysis for Time-Series Data of Real-time TDDFT Naoki TANI, Satoru S. KANO, Yasunari ZEMPO
Analysis on Circularly Polarized Luminescence Properties of Oxaza[7]dehydrohelicene Derivatives Using Knowledge Graph and Mechanics Simulations Yusuke SUGENAMI, Mikito FUJINAMI, Mohamed S. H. SALEM, Shinobu TAKIZAWA, Hiromi NAKAI

View all articles in current issue

Most viewed articles (February 2026)

1

First Calculation of Q-e Values of Polymer Radicals

Released on J-STAGE: May 08, 2024 | Volume 23 Issue 1 Pages A9-A14

Susumu KAWAUCHI

Views: 241
2

First-Principles Calculation Study on Solid Electrolyte Interphase (SEI) in Lithium Ion Battery

Released on J-STAGE: February 20, 2019 | Volume 18 Issue 1 Pages 18-28

Yoshitaka TATEYAMA

Views: 193
3

Anion Intercalation and Selectivity in NiFe LDH: Insights from Neural Network-Enhanced Molecular Dynamics

Released on J-STAGE: April 12, 2025 | Volume 24 Issue 1 Pages 20-26

Tien Quang NGUYEN, Susan Meñez ASPERA, Yingjie CHEN, Kaoru HISAMA, Michihisa KOYAMA

Views: 188
4

Structural Symmetry and Spin Multiplicity of Sumanene Derivative Radical Molecules

Released on J-STAGE: January 05, 2023 | Volume 21 Issue 2 Pages 55-57

Yuika BABA, Hidehiro SAKURAI, Azusa MURAOKA

Views: 161
5

The Study of the Octanol-Water Partition Coefficient by the Computational Chemistry Method

Released on J-STAGE: March 24, 2020 | Volume 18 Issue 5 Pages 241-243

Koichi KODAMA, Arwan SYAH, Kazutomo KAWAGUCHI, Toru MATSUI, Hidemi NAGAO, Yasuteru SHIGETA

Views: 159

Favorites & Alerts

Predecessor

Journal of Chemical Software

Top