大豆作の生産性と技術効率の収束

―パネル単位根検定による計量的分析―

1． はじめに

大豆は，古くより豆腐などなじみ深い食品の原料であり，営農上も稲，麦と共に基幹的な土地利用型作物である．また水稲の裏作として麦作との二毛作の輪作体系の確立に重要な作物であり，水田フル活用のための重要な戦略作物として位置づけられ，新たな大豆政策大綱による拡大推進が講じられているところである．茅野（2005）によって大豆における自給率向上の可能性と大豆作の推進を指摘している．農業政策立案者にとって各地域の大豆生産が傾向として同一方向へ進んでいるか否か，さらにその速度がどの程度であるかを踏まえて政策立案することは重要と思われる．

収束するならば当該地域で同一の方向へ向かっていることとなり一律の農業政策が有効であり，違うなら別々の政策が望ましいと考えられる．これまで経営効率の研究について技術進歩や技術効率を計測する研究が数多くなされてきた．技術進歩を捉える手法としてCaves, Christensen and Diewert（1982）が開発したマルムクイスト指数は，規模に関して収穫一定を仮定し，技術進歩と技術効率に分解できることが明らかにされた．

この指数を用いて多くの研究がなされており，収束問題についても農業全体や米について多くの分析がなされてきた（山口・霍，2004；高松・衣笠，2010）．しかし大豆における計量分析に関する論文は多数あるものの生産性および技術効率の変化を分析した文献は過去になく，戦略作物として推進されている大豆に対する分析は，日本の農業政策，特に自給率向上に向けた政策に新たな知見を生み出すと思われる．また中川他（2012）が示した小麦の生産性によって二毛作（小麦と大豆）の生産性が明らかになると思われる．

本研究は，大豆の生産性や技術効率，技術変化について地域別に分析を行い，生産性や技術効率等の収束を検定しその収束速度を計測する．本研究の構成は，次ぎのようになっている．第2節で指標の計測方法，第3節で単位根検定と収束概念，第4節で分析結果を吟味する．第5節で本研究での分析結果を総括し，最後に結論を述べる．

2． マルムクイスト指数による生産性および技術効率性の計測方法

（1） マルムクイスト指数

マルムクイスト指数は，ある経済主体の効率性が時間を通じ，どの程度変化したかを示す指標である．DEA（Data Envelopment Analysis）を概説すると，第s期の技術水準の下で，第t期のインプットx_tからアウトプットy_tを生産し，経済主体jがn個存在するものとすると，第k番目の経済主体は以下のCRS（constant returns to scale）モデルを解くことにより求めることができる．ただし，θは効率値，λは作業解析で使われる強度変数，インプット要素iはl種類，アウトプット要素rはm種類とする．

  

$$\min \mathrm{\theta }=\mathrm{D}\mathrm{c}\mathrm{r}\mathrm{s},\mathrm{s}({\mathrm{\chi }}_{\mathrm{t}},{\mathrm{y}}_{\mathrm{t}})$$

  

$$\mathrm{s}.\mathrm{t}.–{\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{\lambda }}_{\mathrm{j}}{{\mathrm{\chi }}_{\mathrm{i}\mathrm{j},\mathrm{s}}+\mathrm{\theta }\mathrm{\chi }}_{\mathrm{i}\mathrm{k},\mathrm{t}}\ge 0(\mathrm{i}=\mathrm{1,2},\dots ,\mathrm{l})$$

  

$${\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{\lambda }}_{\mathrm{j}}{\mathrm{y}}_{\mathrm{r}\mathrm{j},\mathrm{s}}\ge {\mathrm{y}}_{\mathrm{r}\mathrm{k},\mathrm{t}}\left(\mathrm{r}=\mathrm{1,2},\dots ,\mathrm{m}\right),{\mathrm{\lambda }}_{\mathrm{j}}\ge 0(\mathrm{j}=\mathrm{1,2},\dots ,\mathrm{n})$$（1）

さらに，制約条件に ${\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{\lambda }}_{\mathrm{j}}=1$ を加えることで規模に関して収穫可変として求めることができる．本研究は4種類の入力，1種類の出力であるため入力指向で計測することとした．

マルムクイスト指数は，基準となる時点の技術水準を固定し，当該技術水準の下で各期の技術効率性により計測する．第s期を基準としたマルムクイスト指数は，以下のとおり．

  

$${\mathrm{M}\mathrm{I}}_{\mathrm{s}}=\frac{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{s}}({\mathrm{\chi }}_{\mathrm{t}},{\mathrm{y}}_{\mathrm{t}})}{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{s}}({\mathrm{\chi }}_{\mathrm{s}},{\mathrm{y}}_{\mathrm{s}})}$$（2）

2期間の幾何平均をとると，

  

$$\mathrm{M}\mathrm{I}={（{\mathrm{M}\mathrm{I}}_{\mathrm{s}}\mathrm{・}{\mathrm{M}\mathrm{I}}_{\mathrm{t}}）}^{\frac{1}{2}}$$

  

$$={\left[\frac{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{s}}({\mathrm{\chi }}_{\mathrm{t}},{\mathrm{y}}_{\mathrm{t}})}{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{s}({\mathrm{\chi }}_{\mathrm{s}},{\mathrm{y}}_{\mathrm{s}})}}\mathrm{･}\frac{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{t}}({\mathrm{\chi }}_{\mathrm{t}},{\mathrm{y}}_{\mathrm{t}})}{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{t}}({\mathrm{\chi }}_{\mathrm{s}},{\mathrm{y}}_{\mathrm{s}})}\right]}^{\frac{1}{2}}$$（3）

ここでマルムクイスト指数を以下のように変形することで，次の要素に分解することができる．

  

$$\mathrm{M}\mathrm{I}=\frac{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{t}}({\mathrm{\chi }}_{\mathrm{t}},{\mathrm{y}}_{\mathrm{t}})}{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{s}}({\mathrm{\chi }}_{\mathrm{s}},{\mathrm{y}}_{\mathrm{s}})}\mathrm{･}{\left[\frac{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{s}}({\mathrm{\chi }}_{\mathrm{t}},{\mathrm{y}}_{\mathrm{t}})}{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{t}({\mathrm{\chi }}_{\mathrm{t}},{\mathrm{y}}_{\mathrm{t}})}}\mathrm{･}\frac{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{s}}({\mathrm{\chi }}_{\mathrm{s}},{\mathrm{y}}_{\mathrm{s}})}{{\mathrm{D}}_{\mathrm{C}\mathrm{R}\mathrm{S},\mathrm{t}}({\mathrm{\chi }}_{\mathrm{s}},{\mathrm{y}}_{\mathrm{s}})}\right]}^{\frac{1}{2}}$$

  

$$=\mathrm{T}\mathrm{E}\mathrm{C}·\mathrm{T}\mathrm{C}$$（4）

TECは技術フロンティアに近づいたことによる影響を示す指数である技術効率性であり，TCはフロンティア自身が変化したことによる影響を示す指数である技術進歩を表している．

これまで規模に関して収穫一定を仮定して技術効率を計測しているが，現実には規模に関して収穫可変の可能生もあるため，規模に関して収穫可変を考慮する．技術効率性は以下のように分解することができる．

TEC=PEC·SEC

PECは規模に関して収穫可変を仮定した技術効率性を表し，SECは規模に関する効率性の変化による影響を表しており，最適な規模との乖離が生産活動に与える影響と解釈され，政策的に規模拡大を推進する上で重要な指数となる．ここでマルムクイスト指数は，各時点での生産性水準ではなく2時点間の変化である．そこで近藤・山本（2004）に倣い生産性水準は，1年目の生産性水準は1年目の技術効率性とし，2年目以降の生産性水準は1年目の技術効率性に時年次以降の生産性変化を累積的に毎年乗じて行くことにより産出した．

他の指数の水準について，技術効率性は1年目の技術効率性，技術進歩等その他の指数は1年目の水準を1とし，次年以降は年次変化を累積的に乗じることにより産出した．

3． 単位根検定による収束の検定

（1） 収束と検定方法

各経済主体の経済パフォーマンスが，時間を通じ同レベルの定常状態に移行することを収束（convergence）という．経済発展が遅れた経済主体がより速いスピードで成長すれば，最終的には，すべての経済主体の経済パフォーマンスは同じような定常水準に収束することとなる．このような収束過程を絶対収束と名付けてられている．しかし，各経済主体がそれぞれ異なる定常水準を持ち，経済パフォーマンスもそれぞれの定常水準に収束する場合がある．このような状態を条件付収束と呼ばれている．以下では収束の検定方法である単位根検定について説明する．

確率変数Y_tが，AR(1)モデルに従うと仮定する．（u_t：ホワイト・ノイズ）

  

$${\mathrm{Y}}_{\mathrm{t}}=\mathrm{\varphi }{\mathrm{Y}}_{\mathrm{t}-1}+{\mathrm{u}}_{\mathrm{t}}$$（5）

初期値をY₀とし逐次代入すると，

  

$${\mathrm{Y}}_{\mathrm{t}}={\mathrm{\varphi }}^{\mathrm{t}}{\mathrm{Y}}_0+{\sum }_{\mathrm{j}=1}^{\mathrm{t}}{\mathrm{\varphi }}^{\mathrm{t}-\mathrm{j}}{\mathrm{u}}_{\mathrm{j}}$$（6）

ここで，

  

$$\left|\mathrm{\varphi }\right|<1\Rightarrow {\mathrm{l}\mathrm{i}\mathrm{m}}_{\mathrm{t}\to \mathrm{\infty }}{\mathrm{Y}}_{\mathrm{t}}={\sum }_{\mathrm{j}=1}^{\mathrm{t}}{\mathrm{\varphi }}^{\mathrm{t}-\mathrm{j}}{\mathrm{u}}_{\mathrm{j}}$$

  

$$\left|\mathrm{\varphi }\right|\ge 1\Rightarrow {\mathrm{l}\mathrm{i}\mathrm{m}}_{\mathrm{t}\to \mathrm{\infty }}{\mathrm{Y}}_{\mathrm{t}}=\mathrm{\infty }$$

つまり，確率変数Y_tが単位根を持たなければ，収束する．よって単位根の有無を検定することにより，収束するか否かを確認できる．具体的には拡張されたディッキーフラー検定（ADF検定）により次ぎの3つのモデルにより推定する．

モデル1：   

$$\begin{array}{c}{\mathrm{Y}}_{\mathrm{t}}=\mathrm{\varphi }{\mathrm{Y}}_{\mathrm{t}-1}+{\sum }_{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{\gamma }}_{\mathrm{j}}{∆\mathrm{Y}}_{\mathrm{t}-\mathrm{j}}+{\mathrm{u}}_{\mathrm{t}}\\ \\ \iff {∆\mathrm{Y}}_{\mathrm{t}}={\mathrm{\beta }\mathrm{Y}}_{\mathrm{t}-1}+{\sum }_{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{\gamma }}_{\mathrm{j}}{∆\mathrm{Y}}_{\mathrm{t}-\mathrm{j}}+{\mathrm{u}}_{\mathrm{t}}\end{array}$$（7）

モデル2：   

$$\begin{array}{c}{\mathrm{Y}}_{\mathrm{t}}=\mathrm{\mu }+\mathrm{\varphi }{\mathrm{Y}}_{\mathrm{t}-1}+{\sum }_{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{\gamma }}_{\mathrm{j}}{∆\mathrm{Y}}_{\mathrm{t}-\mathrm{j}}+{\mathrm{u}}_{\mathrm{t}}\\ \\ \iff {∆\mathrm{Y}}_{\mathrm{t}}=\mathrm{\mu }+{\mathrm{\beta }\mathrm{Y}}_{\mathrm{t}-1}+{\sum }_{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{\gamma }}_{\mathrm{j}}{∆\mathrm{Y}}_{\mathrm{t}-\mathrm{j}}+{\mathrm{u}}_{\mathrm{t}}\end{array}$$（8）

モデル3：   

$$\begin{array}{c}{\mathrm{Y}}_{\mathrm{t}}=\mathrm{\mu }+\mathrm{\delta }\mathrm{t}+\mathrm{\varphi }{\mathrm{Y}}_{\mathrm{t}-1}+{\sum }_{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{\gamma }}_{\mathrm{j}}{∆\mathrm{Y}}_{\mathrm{t}-\mathrm{j}}+{\mathrm{u}}_{\mathrm{t}}\\ \\ \iff {∆\mathrm{Y}}_{\mathrm{t}}=\mathrm{\mu }+\mathrm{\delta }\mathrm{t}+{\mathrm{\beta }\mathrm{Y}}_{\mathrm{t}-1}+{\sum }_{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{\gamma }}_{\mathrm{j}}{∆\mathrm{Y}}_{\mathrm{t}-\mathrm{j}}+{\mathrm{u}}_{\mathrm{t}}\end{array}$$（9）

ここで，β=1–ϕ， ${\sum }_{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{\gamma }}_{\mathrm{j}}∆{\mathrm{Y}}_{\mathrm{t}-\mathrm{j}}$ は拡張項，μは確定項，tはタイムトレンドを表している．モデル2とモデル3の拡張項を除くと

モデル2：   

$${\mathrm{Y}}_{\mathrm{t}}=\frac{1-{\mathrm{\varphi }}^{\mathrm{t}}}{1-\mathrm{\varphi }}\mathrm{\mu }+{\mathrm{\varphi }}^{\mathrm{t}}{\mathrm{Y}}_0+{\sum }_{\mathrm{j}=1}^{\mathrm{t}}{\mathrm{\varphi }}^{\mathrm{t}-\mathrm{j}}{\mathrm{u}}_{\mathrm{j}}$$

  

$$\therefore \left|\mathrm{\varphi }\right|<1\Rightarrow {\mathrm{l}\mathrm{i}\mathrm{m}}_{\mathrm{t}\to \mathrm{\infty }}{\mathrm{Y}}_{\mathrm{t}}$$

  

$${\mathrm{Y}}_{\mathrm{t}}=\frac{1}{1-\mathrm{\varphi }}\mathrm{\mu }+{\sum }_{\mathrm{j}=1}^{\mathrm{t}}{\mathrm{\varphi }}^{\mathrm{t}-\mathrm{j}}{\mathrm{u}}_{\mathrm{j}}$$

  

$$\therefore \left|\mathrm{\varphi }\right|\ge 1\Rightarrow {\mathrm{l}\mathrm{i}\mathrm{m}}_{\mathrm{t}\to \mathrm{\infty }}{\mathrm{Y}}_{\mathrm{t}}=\mathrm{\infty }$$（10）

モデル3：   

$$\begin{array}{c}{\mathrm{Y}}_{\mathrm{t}}=\frac{1-{\mathrm{\varphi }}^{\mathrm{t}}}{1-\mathrm{\varphi }}\mathrm{\mu }+\frac{{\mathrm{\varphi }}^{\mathrm{t}-1}+\left(1-\mathrm{\varphi }\right)\mathrm{t}-\mathrm{\varphi }}{{(1-\mathrm{\varphi })}^{\mathrm{t}}}\mathrm{\delta }+{\mathrm{\varphi }}^{\mathrm{t}}{\mathrm{Y}}_0\\ +{\sum }_{\mathrm{j}=1}^{\mathrm{t}}{\mathrm{\varphi }}^{\mathrm{t}-\mathrm{j}}{\mathrm{u}}_{\mathrm{j}},\therefore {\mathrm{l}\mathrm{i}\mathrm{m}}_{\mathrm{t}\to \mathrm{\infty }}{\mathrm{Y}}_{\mathrm{t}}=\mathrm{\infty }\end{array}$$（11）

ここで，β=0のとき，確率変数Y_tが単位根を持つ場合，すべてのモデルで発散する．またβ<0のとき，モデル1に従うならば絶対収束，モデル2に従うならば，条件付収束，モデル3に従うならば，発散することになる．ここでモデル2に従うということは，β<0かつμ≠0であることを意味し，モデル3に従うというのはβ<0かつμ≠0かつδ≠0であることを意味する．従って，β<0かつμ=0かつδ=0の場合，モデル1に従うことになり絶対収束となる．またβ<0かつμ≠0かつδ=0の場合，モデル2に従うことになり条件付収束と判断できる．また時系列分析の場合，期間が短くなることが多い．そこで単位根検定に加え，標本の大きさを確保するためパネルデータに対応したパネル単位根検定を行う．（Levin et al., 2002; Im et al., 2003; Maddala and Wu, 1999）．（以下，LLC検定，IPS検定，MW検定）．LLC検定では，すべての経済主体に単位根があるか検定するものであり，帰無仮説が棄却されるとすべての経済主体の確率変数Yが長期的にゼロに近づき収束することとなる．IPS検定とMW検定では少なくとも1つの経済主体に単位根があるか検定するものであり，帰無仮説が棄却されると少なくとも1つの経済主体は収束していることになる．

（2） 収束速度

長期的に収束するならば，どの程度の速度で乖離が縮小するかは重要なことである．この速度を計測する指標として，半減期（均衡からの乖離が半分になるのに必要な時間）がある．（7）式または（8）式で求められるϕによって，以下のとおり半減期T_1/2を表すことができる．

  

$$\mathrm{Y}\left(\mathrm{t}\right)={\mathrm{Y}}_0{\mathrm{e}}^{-\mathrm{\varphi }\mathrm{t}}$$

  

$$\mathrm{Y}\left({\mathrm{T}}_{1/2}\right)=\frac{{\mathrm{Y}}_0}{2}={\mathrm{Y}}_0{\mathrm{e}}^{-{\mathrm{\varphi }\mathrm{T}}_{1/2}}$$

  

$${\mathrm{e}}^{-\mathrm{\varphi }{\mathrm{T}}_{1/2}}=\frac{1}{2}$$

  

$${\mathrm{T}}_{1/2}=\frac{\mathrm{l}\mathrm{n}2}{\mathrm{\varphi }}$$（12）

したがって，半減期はln(2)/ϕ=0.69/ϕである．それゆえ，ϕ=0.05の場合，半減期は14年となる．本研究では，1期は1年（12ヶ月）となる．

4． 生産性とその収束結果

（1） 使用した統計資料

計測に用いる資料は，農林水産省の農業経営統計調査大豆生産費の全国と地域別平均値データ（北海道，東北，北陸，関東・東山，東海，近畿，中国，九州）である．計測期間は地域別が公表された2008年から2014年とした¹．生産物は大豆生産量，生産要素は労働，資本，土地，経常財とした，大豆の生産量については収穫量とし，労働は直接投下労働時間，資本は農機具費，賃借料および料金，建物費の合計とし，土地は大豆作付面積，経常財は種苗費，肥料費，農業薬剤費，その他諸材料の合計とした．また資本と経常財は，農業物価統計調査農業生産資材類別年次別価格指数（平成22年基準）でデフレートして求めた．

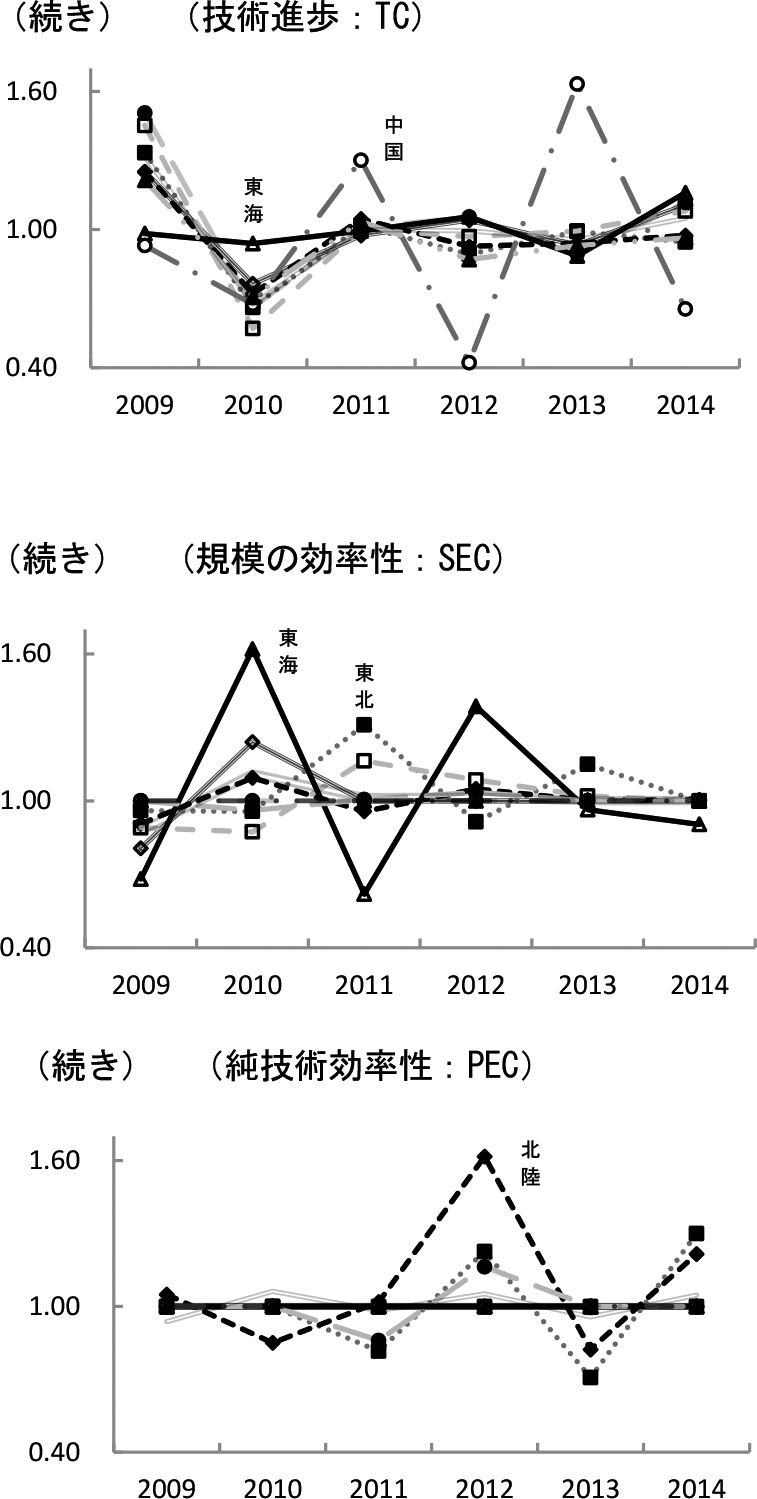
（2） クロスセクションデータを用いた分析

日本の各地域（北海道，東北，北陸，関東・東山，東海，近畿，中国，九州）について，（4）式により求められたマルムクイスト指数，技術効率性，技術進歩，純技術効率性，規模に関する効率性の結果を図1に示した．マルムクイスト指数についてみると北海道の計測値は0.93～1.11で安定しているものの，その他の地域では計測値の変動が大きい結果となった．大豆生産は湿害だけでなく黒根腐病，虫害，地力の低下等多くの影響から生産が安定しないことから，それを反映する結果となった．

図1.

マルムクイスト指数の計測結果

図1.

マルムクイスト指数の計測結果（続き）

表1. マルムクイスト指数の年平均変化率

北海道	1.00
東北	0.98
北陸	1.03
関東・東山	0.98
東海	0.97
近畿	1.01
中国	0.85
九州	0.94

フロンティアに近づいたことによる影響である技術効率性（TEC）の計測値を見ると，2010年に東海（1.62），2012年北陸（1.70）と全国最高となっている．しかし東海は2011年（0.62），北陸は2013年（0.83）に全国で最も低い値になっており，東海と北陸は最高と最低を繰り返す不安定な状態が明らかになった．また計測期間を通じ最高値となる地域が毎年変わる結果から，技術効率性が不安定な状況にあることがわかる．

次ぎにフロンティアが変化したことによる影響である技術進歩（TC）は，計測当初に東海（0.98），中国（0.93）が1.00を下回る結果となり，その他の地域は1.20～1.50と高い値となった．2010年になるとすべての地域で1.00を下回るが，2011年になると中国（1.30）が最高値を記録し，他の地域も1.00程度にもどす結果となった．2012年以降，中国以外の地域は1.00程度に推移しているが，中国は2012年（0.42），2013年（1.63），2014年（0.66）と全国最低と最高を繰り返す結果となった．これらのことから，マルムクイスト指数で最高値になった東海（2010年），北陸（2012年），中国（2013年）について，東海，北陸は技術効率の影響であり，中国は技術進歩の影響であることがわかった．つぎに最適な規模との乖離が生産活動に与える影響である規模の効率性（SEC）は，東海の変動が大きいものの，他の地域はほぼ1.00程度であった．最後に規模に関して収穫可変である純技術効率性（PEC）は，計測期間を通じ変動は少なく，2012年に北陸（1.62）が最高値となった．

（3） 収束に関する検定結果

マルムクイスト指数，技術効率性，技術進歩，規模に関する効率性，純技術効率性の変化について収束するか否かを検定する．山口・霍（2004）にならい，次のような確率変数を作成した．

  

$${\mathrm{Y}}_{\mathrm{t}}={\mathrm{Y}}_{\mathrm{i}\mathrm{t}}^{\mathrm{*}}-{\mathrm{Y}}_{\mathrm{b}\mathrm{t}}$$（13）

（13）式において， ${\mathrm{Y}}_{\mathrm{i}\mathrm{t}}^{\mathrm{*}}$ は各地域におけるマルムクイスト指数等の数値である．ベンチマークであるY_btは地域単位による計測であることを考慮し，各地域の期間平均値とした²．背景となる収束のメカニズムだが，生産性等が低い地域が，高い地域にキャッチアップする傾向にあり，つまり生産性等が低い地域と生産性等が高い地域の差が縮まる傾向にあるということである．大豆は畑作物でありながら田作で栽培されており，輪作体系や有機物の施用など生産性の向上には多くの課題がある．そこで高松・衣笠（2010）が指摘するように，遠方の高生産性地域の影響より，生産環境や気象条件，農業政策が比較的似ている同じ地域内の影響を強く受けることを考慮し，それぞれの地域の期間平均をベンチマークとした．（7）式，（8）式，（9）式に（13）式で計測したY_tを用いADF検定した結果，次のような結論が得た（表2）．短い期間でのADF収束検定であるが，その期間で生産性等の状態を把握することは重要であり，ベンチマークへ向かう絶対収束するか，独自の状態に向かう条件付収束するか，または発散しているかを明らかにすることは今後の政策方針に重要な情報提供をすると思われる．

表2. ADF検定の結果

MI	β(3)		β(2)		β(1)		モデル	結果
北海道	–2.14	**	–2.23	**	–2.04	***	1	絶対
東北	–2.57		–2.73	**	–2.74	***	1	絶対
北陸	–3.09	*	–2.26		–1.47	**	1	絶対
関東	–2.26	*	–2.29		–2.25	**	1	絶対
東海	–2.95		–2.71	**	–1.78	***	1	絶対
近畿	–2.02		–2.18	**	–2.19	***	1	絶対
中国	–3.89		–1.89	***	–1.71	***	1	絶対
九州	–1.79	*	–1.90	***	–1.97	***	1	絶対
TEC	β(3)		β(2)		β(1)		モデル	結果
北海道	–1.82	*	–2.07	*	–1.49	**	1	絶対
東北	–4.87		–2.20	**	–2.08	***	1	絶対
北陸	–3.86		–1.42	**	–1.42	**	1	絶対
関東	–1.94		–0.86		–0.86		1	絶対
東海	–2.85		–3.02	**	–1.71	***	1	絶対
近畿	–2.63		–1.37	**	–1.36	**	1	絶対
TC	β(3)		β(2)		β(1)		モデル	結果
北海道	–1.77		–2.11	*	–2.11	**	1	絶対
東北	–1.62	**	–1.80	**	–1.87	***	1	絶対
北陸	–1.91	**	–1.96	***	–2.03	***	1	絶対
関東	–1.57	**	–1.95	**	–1.98	**	1	絶対
東海	–3.79		–2.38	***	–2.18	***	1	絶対
近畿	–1.79		–1.95	**	–2.01	***	1	絶対
中国	–3.89		–1.89	***	–1.71	***	1	絶対
九州	–1.79	*	–1.90	***	–1.97	***	1	絶対
SEC	β(3)		β(2)		β(1)		モデル	結果
北海道	–1.82	*	–2.07	*	–1.49	**	1	絶対
東北	–1.69	**	–1.57	**	–1.56	***	1	絶対
北陸	–1.79	**	–1.91	**	–1.68	***	1	絶対
関東	–1.94		–0.86		–0.86		1	絶対
東海	–2.85		–3.02	**	–1.71	***	1	絶対
近畿	–2.51	*	–1.01		–1.01	*	1	絶対
PEC	β(3)		β(2)		β(1)		モデル	結果
東北	–2.22	***	–2.21	***	–2.20	***	1	絶対
北陸	–3.62		–1.43	**	–1.44	**	1	絶対
近畿	–2.63		–1.50	**	–1.49	**	1	絶対

1）***は1％，**は5％，*は10％で有意であることを意味する．

2）β(1)はモデル1，β(2)はモデル2，β(3)はモデル3の係数．

3）TEC：中国・九州，SEC：中国・九州，PEC：北海道・関東・東海・中国・九州は数値に変化がなく計測不能．

4）関東は東山（山梨・長野）を含む．

マルムクイスト指数（MI）について，すべての地域はそれぞれの地域の平均値に絶対収束となった．つまり，時間の経過につれ，長期的にはマルムクイスト指数は計測期間平均値を定常状態とすることがわかった．マルムクイスト指数は各地域で変動し，最高値を記録する地域も毎年変わる状態にあるが，収束する方向に働いていることがわかった．技術効率性（TEC）について，（13）式で表される確率変数は単位根を持たず，（8）式や（9）式を推定した場合，切片やタイムトレンドが有意でないことが見出された³．

よって，技術効率性は（7）式に従い絶対収束すると判断された⁴．大豆生産において地域の農業に合わせ，生産技術の開発および営農指導が行われる．各地域内は，自然条件が比較的類似しており生産技術の伝播しやすく同一の方向に成長をしていると考えられる．技術進歩（TC）について各地域において絶対収束するという結果を得た．つまり短期的には各地域で平均値から差があるものの，時間の経過につれ，長期的には各地域の平均値と同じ値になることを意味している．

自由度を増やすとともに，地域間および時系列の異質性に対応するためにパネル単位根検定の結果を示した（表3）．ADF，LLC，IPS，PPのすべての単位根検定においてp値は小さい結果となった．つまりマルムクイスト指数ほかすべての指数において単位根を持たず，収束することが明らかになった⁵．

表3. パネル単位根検定の結果

MI		検定統計量	P値
	ADF	118.97	0.00
	LLC	–17.47	0.00
	IPS	–5.44	0.00
	MW	123.41	0.00
TEC		検定統計量	P値
	ADF	36.93	0.00
	LLC	–6.19	0.00
	IPS	–2.62	0.00
	MW	75.36	0.00
TC		検定統計量	P値
	ADF	106.10	0.00
	LLC	–23.11	0.00
	IPS	–4.86	0.00
	MW	119.09	0.00
SEC		検定統計量	P値
	ADF	42.96	0.00
	LLC	–7.36	0.00
	IPS	–3.15	0.00
	MW	73.45	0.00
PEC		検定統計量	P値
	ADF	12.88	0.01
	LLC	–3.53	0.00
	IPS	–4.84	0.00
	MW	31.55	0.00

1）ADFはAugment Dickey-Fuller検定，LLCはLevin-Lin-Chu検定，IPSはIm-Pesaran-Shin検定，MWはMaddala-Wu検定．

（4） 半減期の比較

（13）式により計測された確率変数により，（12）式によって計測された半減期を表4にまとめた．計測結果から，マルムクイスト指数の半減期は全国値で3.56ヶ月となった．農業全体を計測した高松・衣笠（2010）によると6.4ヶ月であったことを考慮すると妥当な結果と思われる⁶．つぎに技術効率性は5.38ヶ月，技術進歩は4.00ヶ月となった．さらに技術効率を構成する純技術効率性と規模に関する効率性の変化はそれぞれ4.67ヶ月，5.81ヶ月と確認された．技術進歩の収束速度は比較的速く，技術効率性や規模に関する効率性の収束は遅い傾向にあることが明らかになった．

表4. 各地域の半減期

	MI	TEC	SEC	PEC	TC
北海道	4.07	5.59	5.59	―	3.95
東北	3.04	4.00	5.33	3.79	4.46
北陸	5.66	5.85	4.96	5.79	4.10
関東	3.69	9.69	9.69	―	4.20
東海	4.66	4.87	4.87	―	3.82
近畿	3.79	6.10	8.26	5.57	4.15
中国	4.86	―	―	―	4.86
九州	4.23	―	―	―	4.23
全国	3.56	5.38	5.81	4.67	4.00

1）単位は月．

2）関東は東山（山梨・長野）を含む．

低い地域は農機具や改良品種等の伝播は比較的速く取り組まれるが，伝播された技術を地域の気象，土壌条件，農業経営等に対応しながら取り入れるには時間がかかるものと思われる．特に規模に関する効率性は農地のほ場整備率や経営の大規模化などが深く関わるので時間がかかると推察される．さらに地域別に見ると，マルムクイスト指数では東北が最も短く3.04ヶ月，反対に最も長い地域は北陸5.66ヶ月であった．つぎに技術効率性では，東北が最も短く4.00ヶ月であり，最も長いのは関東・東山で9.69ヶ月となった．技術進歩では東海が3.82ヶ月で最も短く，中国が4.86ヶ月で最も長かった．

5． おわりに

大豆生産の5つの効率性指標を計測した結果，マルムクイスト指数についてみると北海道は安定しているが，その他の地域では計測値の変動が大きく生産が不安定であることがわかった．技術効率性についても，東海は最高と最低を繰り返す不安定な状態が明らかになった．技術進歩は中国の変動が大きいものの，その他の地域は1.00程度であり同様の動きになっていることが明らかになった．収束については，パネル単位根検定の結果からすべての指標で収束することがわかった．

すなわちそれぞれの地域の生産環境に応じて収束することが示唆された．収束速度の全国平均はマルムクイスト指数（3.56）が最も速く，次いで技術進歩（4.00），技術効率性（5.38）となった．技術効率性の結果から，伝播された技術を各地域で効率的に取り入れることに時間を要することが示された．本研究の結果から生産性や技術効率性の変動は大きいものの，それぞれの地域内で収束が見られる．

大豆生産の向上は，農業経営的な推進だけでなく，被害（湿害，黒根腐病等）や地力の低下，収穫ロスなどに対応した生産技術の面も踏まえた検討が必要であろう．特に近年の転作率の上昇により大豆作付頻度が増加しているため，地力維持や病害虫リスクの軽減に資する輪作体系の確立が必要と思われる．今後の研究課題として主要農作物や戦略作物など多様な作物を生産しており，生産性の比較検討をするとともに，収束仮説を背景とした作物間の技術伝播による影響を明らかにすることは重要であると考える．

また半減期の計測から，各地域ともに比較的早い速度で技術伝播されることがわかった．地域の生産環境に合った生産技術や営農指導等が行われれば急速に伝播することが可能であり，全国的に生産性の向上を実現できると思われる．

謝辞

本研究にあたり，神戸大学名誉教授の山口三十四先生，神戸大学教授の衣笠智子先生にご指導とご指摘を頂きました．心から感謝の意を表します．なお，本研究はJSPS科研費JP26292118の助成を受けた．

注

1  地域別データが2008年から公表されたため，計測期間が短くなっている．しかし一つの政策期間は3年程度であるため，地域別の大豆政策の状況を把握するのに重要であり，結果は現実を反映した重要な情報源である．また十分なデータ数を確保しているパネル分析でも同様の結果を得ているため，結論に影響ないと考えられる．

2  収束問題の可能生として，高松・衣笠（2010）が述べているように，地域の平均値へ収束する可能性と，その場合にベンチマークを地域の期間平均値として分析することを指摘している．表1および表2の結果から絶対収束とパネル単位根検定による収束から地域の平均値へ収束することが確認できたと考えられる．

3  本研究は，パネル単位根検定を用いた仮説検定が主眼であるため，定数項およびタイムトレンドのパラメータを省略した．

4  中国と九州地域は計測期間を通じ技術効率性（TEC）に変化なし．他にSECとPEC（関東・東山，東海，中国，九州）も同様．

5  時系列分析だけでなく，クロスセクションデータを加味したパネル単位根検定を取り入れることで，データ数の確保および単位根検定の頑健性を証明できたと考える．

6  非定常モデルを用いた農業の半減期を計測した先行研究（高松・衣笠，2010）がMI 6.4ヶ月，TEC 9.2ヶ月，TC 5.3ヶ月，SEC 10.5ヶ月であることを考慮すると，妥当な結果が得られた．ほかにソローモデルによる計測との比較は今後の課題としたい．

引用文献

•  茅野 甚治郎（2005）「食料需給構造と自給率の低下」『農業経済研究』77(3)，97–112．
•  近藤 功庸・ 山本 康貴（2004）「減反開始期以降におけるわが国稲作生産性変化に対する地域別貢献度分布」『2004年度日本農業経済学会論文集』7(1)，83–89．
•  高松 良樹・ 衣笠 智子（2010）「日本農業の技術効率性と収束―マルムクイスト指数およびパネル単位根検定を用いた計量的研究―」『経済政策ジャーナル』7(1)，49–67．
•  中川 雅嗣・ 衣笠 智子・ 山口 三十四（2012）「日本小麦の全要素生産性とその収束―パネル単位根検定を用いた計量分析―」『国民経済雑誌』205(5)，69–80．
•  山口 三十四・ 霍　 靈光（2004）「包絡線分析法による旧ソ連諸国の農業技術効率性と収束の分析」『農林業問題研究』40(3)，339–347．
•  Caves,  D. W.,  Christensen,  L. R. and  Diewert,  W. E. (1982) The economic theory of index number and the measurement of input, output and productivity. Econometrica, 50, 1393–1414.
•  Im,  K. S.,  Pesaran,  M. H. and  Shin,  Y. (2003) Testing for unit roots in heterogeneous panels. Journal of Econometrics, 115, 53–74.
•  Levin,  A.,  Lin,  C. and  Chu,  C. J. (2002) Unit root tests in panel data: Asymptotic and finite sample properties. Journal of Econometrics, 108, 1–24.
• Maddala, G. S. and Wu, S. (1999) A comparative study of unit root tests with panel data and a new simple test. Oxford Bulletin of Economics and Statistics, 61(S1), 631–652.