2023 Volume 71 Issue 6 Pages 386-397
2023 Volume 71 Issue 6 Pages 386-397
Various stresses and strains are generated on the surface and inside of pharmaceutical tablets when an external force is applied. In addition, stresses in various directions can remain on the surface and inside the tablets because they are generally prepared by compaction of pharmaceutical powders using dies and punches. As it is difficult to measure the stress and strain generation in the tablets experimentally, a numerical simulation was applied by employing a finite element method (FEM). An elastic model is often used to represent stress and strain generation after loading an external force to tablets, and the Drucker–Prager cap (DPC) model has been widely recognized for representing the remaining stress distributions during the compaction of powder to tablet form. Firstly, this article describes an FEM simulation of the stress generation on the surface of the scored tablets after loading the bending force from the back side of the tablets. Next, the FEM simulation was introduced to determine the effect of diametrical compression on the stress and strain generation in the tablets by comparing the results measured experimentally. Furthermore, the residual stresses remaining inside the tablets were simulated using FEM, in which powder compaction was represented as the DPC model. A clear difference was observed in the residual stress distributions between the flat and convex tablets. This indicates that FEM simulation is useful for achieving a science-based understanding of critical quality attributes in various types of tablets.
Pharmaceutical tablets are the most popular solid dosage forms compared to other types, such as powders, granules, and capsules.1–3) The critical quality attributes (CQAs) required of tablets are sufficient mechanical strength, and rapid disintegration and dissolution rates.4,5) However, a contradiction in these CQAs often arises to satisfy the quality target product profiles. For example, mechanically stronger tablets are closely related to the retardation of disintegration and dissolution times. In tablet development, it is crucial to balance the contradictory relationships between the CQAs. Various stresses and strains can remain on the surface and inside the tablets because they are generally prepared by compaction of pharmaceutical powders using dies and punches. Therefore, it is likely that the CQAs are significantly affected by the stress and strain distributions in the tablets. As it is difficult to measure the stress and strain generations experimentally, a numerical simulation has often been applied by employing a finite element method (FEM). Elastic and elastic-plastic models are generally used to represent the stress and strain generations in tablets. The simple elastic model can be applied to simulate the stress and strain generations after loading the external force on tablets. That is, mechanically weak areas in the tablets can be specified using a simple elastic model.6,7) In addition, a more complicated elastic-plastic model must be introduced to simulate the residual stress distributions after powder compaction. For this purpose, the Drucker–Prager cap (DPC) model has been recognized to represent the powder compaction process.8–20) Strictly speaking, the elastic-plastic parameters are not constant, and their values change slightly with the relative density of powder compaction. To enhance the accuracy of residual stress simulation in tablets, a density-dependent DPC model has been developed.21–24) However, the improved model has considerable disadvantages, as follows14,21): (1) DPC parameters must be determined over a range of relative densities, and it is very time consuming; (2) to account for the variation in the elastic-plastic material parameters accompanying the evolution of the relative density, user-defined computer software must be implemented within the commercial FEM package. This may occasionally cause validation problems in computer software25); (3) the density-dependent model requires a much longer time for computer processing.
In this review, the effect of tablet shape on the stress and strain distributions generated by loading the external force was demonstrated,26–28) with particular focus on the score shape on the tablet surface. This is due to tablets often being divided into halves to adjust the effective dose of active pharmaceutical ingredients (APIs). Handling ease and dividing uniformity are critical characteristics of scored tablets.29–31) It has been reported that more than 10% of the weight deviation between the two pieces of tablet halves was observed in over 40% of commercial products.32) To improve the quality of scored tablets, it is valuable to identify mechanically weak areas in the tablets after the loading of external force.26–28) Furthermore, attention was given to the elastic-plastic model for simulating the stress distribution remaining in the tablets after the compaction of pharmaceutical powders and the ejection of compressed tablets as the reason for the remaining stresses in the tablets closely related to CQAs. Studies were investigated in which the classical DPC model was employed due to its ease of application.33)
The United States Food and Drug Administration (FDA) published a Guidance for Industry that addresses tablet scoring to ensure the quality of scored tablets. As a part of the FDA review process for oral solid dosage forms, the guidelines provide testing criteria for scored tablets.34) In the European Pharmacopeia, a subsection that describes scored tablet uniformity tests has also been included, outlining that poorly performing scored lines is a quality defect.35) It is recognized that force loading from the back of the scored surface results in a more uniform division of scored tablets.36) Miura et al.37) reported that scored tablets that are three times wider and two times deeper than conventionally scored tablets were divided easily by hand into equal halves with a small weight variation. Furthermore, Ito et al.38) demonstrated that the dividing uniformity of tablets is greatly influenced by the shape of the scored surfaces. In previous studies, including the authors’,6,7,26–28) the scored tablet was represented as a continuum elastic model. Young’s modulus (E) and Poisson’s rate (ν) were estimated as elastic parameters from a stress-strain curve determined using a test formulation, and these values were used in the FEM simulation. In the past, stress and strain simulations were performed assuming that the tablets were composed of a single material. However, real tablets are prepared by mixing several powders to improve their pharmaceutical characteristics. This review focused on powder mixtures composed of lactose (LAC), corn starch (CS), microcrystalline cellulose (MCC), and magnesium stearate (MgSt).26) LAC was used as the diluent, CS as the diluent and disintegrant, MCC as the diluent and binder, and MgSt as the lubricant. Figure 1 shows the geometry of the scored tablets prepared by the compaction of the mixture powders described above. The depth scores were 0.50, 0.75, 1.00, and 1.50 mm. The score angles were 45, 60, and 75°. An external bending force (100 N) was then applied to the tablets (Fig. 2). The principal stresses are defined as stress tensor elements when the three-dimensional stress coordinate is rotated such that the shear stress components become zero. They are represented as the maximum (σ1), intermediate (σ2), and minimum (σ3) principal stresses. Similarly, the general strains are represented as maximum (ε1), intermediate (ε2), and minimum (ε3) principal strains. Figure 3 shows the σ1 value as a representative of the generated stresses on the top surface of the scored tablet after loading the external force. Substantial tensile stress occurred along the score line, and stress increased with increasing score depth. An exceptionally large σ1 value is brought about by the force generated in an extremely narrow area of the score tip (approx. 145 MPa). It is likely that the value observed in the FEM simulation cannot be directly compared to the experimental results. Although the shape of the score tip was set as a fillet surface to avoid generating a singular point, the edge of V-shaped notches often caused stress concentration. Nevertheless, FEM simulations can be effectively utilized to predict experimental data based on regression analysis, as discussed later. The effect of the score angle on the σ1 value was limited. Weak tension was generated at the other site of the top surface apart from the score line when the score was shallow (0.50–0.75 mm). These findings indicate that score depth is more important than score angle for ease of subdivision and halving equality of score tablets.29,30)



Diametrical compression force was applied to the scored tablets to determine the stresses generated on the surfaces of scored tablets. The results are shown in Fig. 4. Weak compression stress was observed in a limited area on the contact surface of the tablet when an external force was applied. A wide range of tensile stresses appeared on the surface in the direction of the diametrical compression axis. The area became wider with score depth, but the effect of the score angle was limited. The dominant component in the wide range of the σ1 value is tensile strength, which acts from the center in the orthogonal direction to the compression axis. To verify the simulation results experimentally, scored tablets with various score depths and angles were prepared, and the dividing strength, halving equality (defined as FD values), and hardness of these tablets were measured. The smaller the FD values, the better was the halving equality. The results are summarized in Table 1. These values were strongly dependent on the score depth and decreased with the increasing depth of the score shape. In contrast, the score angle had only a minimal effect on mechanical values. When the score shape was shallow (0.50–0.75 mm), the FD value was extremely large and no longer effective as a score line. Less than 1% of the FD value is acceptable for the clinical use of subdividing tablets, in which the therapeutic dose of a drug must be strictly controlled.7,39) A deep score (approx. 1.50 mm) is required to ensure good halving equality. The two-way ANOVA suggested that both dividing strength and halving equality were significantly affected by the score depth, angle, and their interaction, although the effect of score depth on these mechanical characteristics was predominant. Hardness was significantly affected only by score depth. Figure 5 shows the relationship between the experimental values of dividing strength, halving equality, and hardness with the maximum principal stress around the score line after loading the bending force or diametrical direction force. Increasing the σ1 value resulted in an improvement in the dividing ease and halving equality. However, the tablet hardness decreased with increasing σ1 value. Furthermore, the effect of the angle of the score line on the loading axis of the external force is investigated (Fig. 6). The horizontal strain increased when the angle of the scored line to the breaking force was set to 90°. Turning the angle of the score line to 45° resulted in the maximum principal strain (ε1) value generated along the score line. As the score depth increased, this tendency also increased. The potential strain generated along the score line is closely related to the breaking strength of the tablets. When the angle of the score line was changed to 0°, a very strong ε1 value appeared only on the score line. Similar phenomena were observed regardless of the differences in the score depth, although the absolute value of the strain on the scored line increased with increasing score depth. The strain decreased markedly when the angle of the score line to the compression axis changed from 0 to 45 and 90°. These findings agreed well with the results reported by Podczeck et al.9,40) The stress values at failure were predicted to be similar for tablets tested at an angle of 45° or above, whereas at lower test angles, the predicted breaking loads were up to three times greater. To visualize the relationships between the ε1 value and various factors, the response surfaces for the ε1 value were represented using RSM. Figure 7 shows the ε1 value estimated as a function of the angle of the score line to the compression axis, score angle, and score depth. The ε1 value was strongly dependent on the angle of the score line to the compression axis and decreased as the angle increased from 0 to 45 and 90°. The ε1 value was also affected by the score angle and depth, but their effects were rather weak compared to the angle of the score line to the compression axis.

| Depth, h (mm) | Angle, θ (°) | Dividing strength (N) | Halving equality FD value (%) | Hardness(N) |
|---|---|---|---|---|
| 0.50 | 45 | 79.05 ± 1.13 | 57.94 ± 0.67 | 33.33 ± 1.53 |
| 0.75 | 45 | 71.21 ± 1.13 | 53.83 ± 0.66 | 28.00 ± 1.00 |
| 1.00 | 45 | 63.37 ± 2.04 | 3.04 ± 0.86 | 25.67 ± 1.53 |
| 1.50 | 45 | 32.99 ± 1.50 | 0.66 ± 0.04 | 24.00 ± 1.00 |
| 0.50 | 60 | 70.23 ± 2.04 | 55.85 ± 0.33 | 32.33 ± 0.58 |
| 0.75 | 60 | 65.66 ± 0.98 | 9.69 ± 0.34 | 27.33 ± 0.58 |
| 1.00 | 60 | 61.09 ± 1.50 | 2.64 ± 0.17 | 25.33 ± 1.53 |
| 1.50 | 60 | 26.79 ± 2.26 | 0.35 ± 0.33 | 23.67 ± 1.15 |
| 0.50 | 75 | 60.76 ± 1.96 | 53.27 ± 0.69 | 31.67 ± 0.58 |
| 0.75 | 75 | 55.53 ± 1.13 | 7.68 ± 1.55 | 28.33 ± 0.58 |
| 1.00 | 75 | 51.29 ± 1.50 | 3.67 ± 0.80 | 26.67 ± 1.15 |
| 1.50 | 75 | 22.87 ± 1.13 | 0.83 ± 0.33 | 21.33 ± 2.08 |
Each datum represents the mean ± standard deviation (S.D.) for three determinations.

A: dividing strength; B: halving equality; C: hardness.


A: the x and y axes represent the angles of the score line to the compression axis and score angle, respectively, and the score line to the compression axis and score angle, respectively, and the score depth was set at 1.0 mm; B: the x and y axes represent the angles of the score line to the compression axis and score depth, respectively, and the score angle was set at 60°; θ: score angle; h: score depth.
For self-medication, it is important to develop patient-friendly tablets that are uniform and easy to handle. In this context, we focused on so-called “Karate” tablets, i.e., concavely curved scored tablets (CCSTs), as schematically illustrated in Fig. 8.28) Recently, the optimal preparation conditions were investigated for CCSTs containing theophylline as a model API.28) Statistical optimization of CCSTs was performed based on the design of experiments as well as the response surface method41) incorporating a thin-plate spline intereoration.42) The optimal shape of the tablet shown in Fig. 8C was selected. This shape indicated a better dividing uniformity, sufficient hardness, and rapid disintegration time. If we focused on dividing uniformity only, the tablet shape shown in Fig. 8A was the better choice compared to other CCSTs, but the shape shown in Fig. 8C was finally selected as the optimal one that satisfied other characteristics simultaneously. To implement the FEM simulation, the CCST with a concave curvature radius of 15 mm was represented as a continuum elastic model. Figure 9 shows the stress distributions after applying a bending force of 100 N from the back of the flat surface on the opposite side of the CCST. Extremely strong tensile stresses became concentrated along the tip of the score line in the x–y cross-section (Fig. 9A). Similar phenomena were observed in the y–z cross-section (Fig. 9B). In addition, weak tensile stresses (<30 MPa) were generated over the entire surface. The tensile stress concentrated beneath the tip of the score line was 277 MPa. No significant difference in the tensile stresses was observed in the CCSTs, irrespective of the differences in the concave curvature radii. This value was evidently greater than 145 MPa, which has been shown in the case of flat-faced scored tablets26,43) (Fig. 3). The maximum tensile stress with a similar shape to the CCST without the score line on the concavely curved surface was calculated to be 44 MPa,28) suggesting that the scored line fabricated on the concavely curved surface was crucial for the efficient generation of tensile stresses. It was suggested that the unique shapes of the CCSTs induced strong tensile stresses just under the tip of the score line.

Curvature radius of A: 8.9 mm; B: 11.2 mm; C: 15.0 mm; D: 22.7 mm.

A: normal stress in x-y cross section; B: normal stress in y–z cross section.
To make the simulation close to the realistic tableting process, the upper punch was removed after the loading reached the target value, and the die was then detached from the powder bed (Fig. 10). In addition to the elastic parameters, such as Young’s modulus (E) and Poisson’s rate (ν), the parameters of plastic deformation and friction of powders are required to simulate the remaining stresses of tablets using the DPC model.44,45) The model is composed of two invariants: the first being Cauchy stress (l1) and the second invariant of the deviator stress (J2). These invariants are represented as follows:
 | (1) |
 | (2) |

Powder compaction was modeled using the DPC model. An axisymmetric two-dimensional model (right half) was used. Residual stress was simulated under unconstrained conditions.
The E and ν values were calculated based on the variation in the axial stress (σZ) with the axial strain (εZ) and stress path during the compaction of powders.15,46) The stress path is expressed by a plot, in which the x- and y-axes are the equivalent hydrostatic pressure stress (p) and the square root of the secondary stress invariant (J21/2), respectively. The εZ value is given as the ratio of the powder height during compaction (Z) to the initial height (Z0):
 | (3) |
The bulk modulus K and shear modulus G were defined as follows:
 | (4) |
 | (5) |
where the superscripts m and h denote the values at points where the compression pressure (σZ) is the maximum and J21/2 is zero. The E and ν values can be determined using the K and G values, as follows:
 | (6) |
 | (7) |
Figure 11 shows the yield surface of the DPC model. The yield surface is expressed as a shear failure segment (Ys), compaction cap segment (Yc), and expansion cap segment (Yt). The shear envelope function is expressed as follows:
 | (8) |
where σc is the cohesion parameter, αy is the internal friction coefficient, and A and βy are shear envelope parameters. When l1 is zero, the value of J21/2 is equal to the cohesion (σ0):
 | (9) |
The cap segment that intersects the equivalent pressure-stress axis is an elliptical curve with constant eccentricity in the l1-J2 plane, which is represented as follows:
 | (10) |
where H is the step function. Rcy is the compaction cap parameter and K0 is a parameter that shows the current transition point at which the compaction cap surface intersects the shear envelope portion. The expansion cap function Yt is an elliptical function combined with a step function (H):
 | (11) |
where, Rty is the expansion cap parameter. Fossum and Fredrich have reported at typical cap-hardening law47):
 | (12) |
where εvp is the plastic volume strain, X0 is the intersection of the compaction cap and the l1 axis. Xi is the initial yielding pressure of X0 at which the cap affects the plasticity model. W1c is the maximum possible plastic volumetric strain. D1c and D2c are the cap hardening exponential terms, given in units of 1/MPa and 1/MPa2, respectively. In soft materials, such as tablets prepared by powder compaction, the D2c value can be regarded as zero, and equation 12 can be rewritten as48):
 | (13) |
The shear envelope parameters were determined from the powder compression data. The plastic deformation parameters were determined using the εvp value, defined as follows:
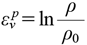 | (14) |
where ρ is the density of the powder bed during compression and ρ0 is the initial density.

The model is composed of an expansion cap (Yt), a shear envelope (Ys), and a compaction cap (Yc). It was hypothesized that the shear envelope could be represented by a simple linear model. K0 is the current transition points at which the compaction cap and shear envelope intersect, and Ki is the initial value of K0. X0 is the current intersection point of the compaction cap and l1 axis, and Xi is the initial value of X0.
Model tablets were prepared using direct compression powder mixtures. The component ratios of the powder formulations are presented in Table 2. These ingredients (LAC, CS, and MCC) were blended in advance and then further blended after adding 2% MgSt. Briefly, the following conditions were employed: tablet diameter, 8 mm; mixture powder, 200 mg; and compression force, 8 kN. No tablet was prepared with formulation 2 (CS only, Table 2). Flat-faced (FLAT) and convex (R16 and R12) tablets were prepared, where R16 and R12 represent curvature radii of 16 mm and 12 mm, respectively. As mechanical characteristics of tablets, the tensile strength (TS) and the disintegration time (DT) were measured.
| Rp.a) | LAC | CS | MCC |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | 1/3 | 2/3 | 0 |
| 5 | 2/3 | 1/3 | 0 |
| 6 | 0 | 1/3 | 2/3 |
| 7 | 0 | 2/3 | 1/3 |
| 8 | 1/3 | 0 | 2/3 |
| 9 | 2/3 | 0 | 1/3 |
| 10 | 1/3 | 1/3 | 1/3 |
Figure 12 shows triangle contour diagrams49,50) for typical DPC parameters predicted based on special cubic equations as a function of the quantity ratio of LAC, CS, and MCC (coded form in Table 2). The elastic parameters E and ν were quantitatively predicted as R2 = 0.9962 and R2 = 0.9862, respectively. A higher quantity of LAC leads to an increase in E and a decrease in ν. Materials with a higher E and a lower ν are more resistant to elastic deformation; therefore, LAC contributes to the hardening of tablets. In contrast, the formulations containing a large amount of MCC showed lower E and higher ν, suggesting that MCC works as an elastically deformable excipient in the tableting process. Similar to the elastic parameters, the d0 value was well predicted (R2 = 0.9905). The contour diagram of d0 suggests that the powder bed was more tightly packed when the formulation contained a large amount of LAC. Regarding the plastic deformation parameters, a fairly good prediction of the W1c was obtained (R2 = 0.9892). A higher amount of LAC induced a lower W1c, indicating that the LAC particles were much harder than those of CS and MCC. Plastic deformation tended to occur when a large quantity of MCC was formulated. The prediction of the Rcy level was somewhat poor with R2 = 0.9431. The predicted θ, σ0 and D1C values were even poorer at R2 = 0.8660, R2 = 0.8764, and R2 = 0.8968, respectively. The Xi value was not predictable (R2 = 0.4692). However, highly sensitive parameters to the FEM simulation, such as the E, ν, d0, and W1c values, were well predicted, suggesting the adequacy of the FEM simulation of the remaining stresses in the tablets composed of LAC, CS, and MCC.

R2: coefficient of determination; R2(adj): adjusted R2 with degrees of freedom; A: Young’s modulus (E, GPa); B: Poisson’s ratio (ν); C: initial density (d0, g/cm3); D: plastic deformation parameter (W1c).
Figure 13 shows the maximum and minimum principal stresses (σ1 and σ3) and the von Mises equivalent stress (σVM) distribution maps for the FLAT, R16, and R12 tablets prepared with powder formulation 10 in Table 2 as an example under unconstrained conditions. The other formulations showed similar distribution tendencies, although the absolute strength differed among the formulations. For instance, strong residual stresses remained in formulations 1, 3, 6, 8, and 9, as these formulations contained a large quantity of LAC51) or MCC.52) Relatively weak stresses were observed in formulations 4, 5, and 7, in which a large quantity of CS53) was included. The principal stresses, σ1 and σ3 values, were obtained by the coordinate rotation of x- and y-axes normal stresses such that the shear stress became equal to zero. Therefore, the strength and direction of the stresses remaining at specific sites in the tablets could be identified. Large differences in residual stresses were observed between FLAT and convex tablets (R16 and R12). Although the FLAT tablets showed almost uniform distributions of σ1 and σ3 values, the σVM value was biased toward the upper die wall. In contrast, an eccentrically located stress distribution was observed in convex tablets. This tendency increased with an increasing in the steepness of tablet curvature. A positive value of σ1 indicates that the tensile force acts on a small discrete area, which is divided by the small mesh set prior to the FEM analysis. In the area close to the die wall for the R16 and R12 tablets, the tensile strength direction of σ1 was almost parallel to the compression axis. With increasing distance from the die wall, the tensile stress inverted to the compressive force (negative value) and then re-inverted to the tensile force in both R16 and R12 tablets (Figs. 13B, C). A weak compressive force remained in the central area, neighboring the upper and lower punches. As σ3 values at the die wall area in the R16 and R12 tablets were highly negative (Figs. 13E, F), the compressive force remained in an orthogonal direction to the σ1 stress axis (i.e., the σ3 stresses acted along the vertical direction to the stress map plane in the area close to the die wall). The σ3 values changed to positive values in the inside area; therefore, the tensile force remained. The shape of the tablets significantly affected the distribution of the residual stress. In the R16 and R12 tablets, a much higher pressure was loaded from the punches in the peripheral area than in the central area. The FLAT tablet showed a stress distribution that was clearly different from those of the R16 and R12 tablets. Many studies54–56) have stated that significant differences in stress distributions arise from tablet shapes. For example, Diarra et al.54) reported that an increase in the relative density in the area close to the die wall corresponded to the surface steepness of the convex tablets. Similarly, Sato et al.8) clarified that strong stress was generated along the peripheral area of the punch surface when preparing convex tablets. Our findings33) also showed specific distributions of tensile and compression forces in convex tablets such as the R16 and R12. It is noteworthy that residual stress still exists at specific sites in the convex tablets, even though sufficient fluidity of each powder formulation was achieved by mixing 2% MgSt.

A: σ1 in FLAT; B: σ1 in R16; C: σ1 in R12; D: σ3 in FLAT; E: σ3 in R16; F: σ3 in R12; G: σVM in FLAT; H: σVM in R16; I: σVM in R12.
A partial least square (PLS) regression57) was used to examine the relationships between input variables (residual stresses; σ1, σ3 and σVM) and output variables (tablet characteristics; TS and DT), and the PLS models were evaluated using a leave-one-out cross-validation (LOOCV) method. In LOOCV, the PLS model is built with n-1 data, and the model is then validated by the remaining data. The modeling and validation processes were repeated n-times, sequentially changing one datum left. As judgment statistics for the optimal PLS model (to determine the number of latent factors), the root mean PRESS was employed, which was defined as the square root of the average of PRESS (predicted residual sum of squares) values across all output variables. For other general statistics, R2 and Q2 were employed as measures of the prediction ability. The R2 value is defined as 1-RSS/TSS, where RSS is the residual sum of squares, and TSS is the total sum of squares. The Q2 value was defined as 1-PRESS/TSS. The closer Q2 is to R2, the greater the robustness of the relevant PLS model. Variable importance in projection (VIP)58–60) is a measure of the importance of each input variable in PLS modeling. A total of 27 FLAT, R16, and R12 tablets were used for the PLS regression analysis. Stress values at 300 sites were employed as input variables, composed of 100 locations each for σ1, σ3, and σVM values on the cross-sectional surface of the tablets. These numerical data were sequentially selected and assigned from the lower left to the upper right in the longitudinal direction. The TS and DT values were used as output variables, where the DT values were transformed to logarithmic form to move them closer to the normal distribution.
An excellent relationship between the experimental and predicted values was observed for the FLAT, R16, and R12 tablets (Fig. 14). The Q2 values were close to R2, suggesting the high reproducibility and robustness of PLS for predicting the TS values. Prediction of the logDT values was considered as acceptable but somewhat worse when compared with the TS values, especially in the case of the R12 tablet. The TS values may simply relate to the residual stress of tablets, which will be dependent on mechanical properties such as the density distribution and elastic-plastic deformations. In contrast, it is likely that tablet disintegration undergoes the wetting of the disintegration media, intrusion of the media, swelling, and destruction. In addition to the residual stresses, the other factors described above may be partly involved in predicting the logDT values.61–63) In a practical sense, however, a fairly good prediction was achieved with PLS regression as a function of numerical data simulated by FEM.

R2: coefficient of determination; Q2: cross-validated R2 with LOOCV; A: TS in FLAT; B: TS in R16; C: TS in R12; D: logDT in FLAT; E: logDT in R16; F: logDT in R12.
Figure 15 shows the VIP maps for predicting the TS values. It is recognized that VIP values less than 0.8 are meaningless.58,60) The VIP values of σ1 stress in the R16 and R12 tablets were considerably larger than 0.8 for the prediction of TS values in the area close to the die wall and the values in the area close to the upper and lower punches, whereas the central area did not contribute to the prediction of TS values (Figs. 15B, C). In contrast, no clear tendency was seen in the FLAT tablet and the important areas distributed at random on the whole VIP map (Fig. 15A). The VIP values of σ3 in R16 and R12 tablets were similar to those of σ1 (Figs. 15E, F). In particular, the areas close to the die wall and the upper punch were important for prediction of the TS values (Figs. 15E, F). In contrast, the significant area in the FLAT tablet (Fig. 15D) was different from those of the R16 and R12 tablets. The area close to the lower-center part was involved with the prediction of characteristics in the FLAT tablet. VIP maps of σVM were similar to those of σ1 and σ3 (Figs. 15G–I), because the σVM value was calculated from σ1 and σ3 values. Again, the σVM values in the peripheral area were important compared with the central area in the R16 and R12 tablets (Figs. 15H, I), which was different from the FLAT tablet (Fig. 15G). VIP maps for log DT were similar to those of TS (Fig. 16). In R16 and R12 tablets, the peripheral area was important for prediction of logDT. A clearly different tendency was seen in the FLAT tablet.

A: σ1 in FLAT; B: σ1 in R16; C: σ1 in R12; D: σ3 in FLAT; E: σ3 in R16; F: σ3 in R12; G: σVM in FLAT; H: σVM in R16; I: σVM in R12.

A: σ1 in FLAT; B: σ1 in R16; C: σ1 in R12; D: σ3 in FLAT; E: σ3 in R16; F: σ3 in R12; G: σVM in FLAT; H: σVM in R16; I: σVM in R12.
PLS produced a good prediction of tablet characteristics as a function of numerical data simulated by FEM. The VIP maps were effective in understanding which area in the residual stress was important for predicting TS and logDT. In the case of the R16 and R12 tablets, the compaction force in the peripheral area, which was transmitted from the punch surface to the powder bed, must be stronger than that in the central area. However, the powder bed was compressed more uniformly in the FLAT tablets, explaining why the VIP map of the FLAT tablet is evidently different from those of the R16 and R12 tablets.
FEM simulations were used to investigate the mechanical stress on the top and lateral surfaces of the scored tablets after the application of external forces. When a bending force was applied, a strong tensile stress was generated along the score line, which increased with the score depth. A wide range of tensile stresses was generated on the top and lateral surfaces of the scored tablets after applying diametrical compression. The area became wider as a function of the score depth. A reasonable relationship between the FEM simulation and experimental results was observed, suggesting that FEM simulation is advantageous for designing scored tablets. For diametrical compression, considerable differences were observed in the strain distribution depending on the angle of the score line to the diametrical compression axis, i.e., 0, 45, or 90°. The strain values increased with increasing score depth. Employing the unique shape of the CCST, it was recognized that tensile stress was easier to generate along the tip of the score line, suggesting that a sufficiently good dividing uniformity was achieved. The key parameters of the DPC model for the FEM simulation were quantitatively predicted as a function of the quantity ratios of LAC, CS, and MCC. Furthermore, the TS and logDT values of the tablets were well predicted using PLS regression analysis as a function of the simulated residual stresses in the tablets. The residual stresses were weak and uniform in the FLAT tablets. In contrast, considerably biased stresses remained in both the R16 and R12 convex tablets. In the R12 tablet, residual stresses significantly affected the tablet characteristics, and they were located in the peripheral area, particularly in the area close to the die wall. The strength of the residual stress was largely dependent on the components of the formulations, but the distribution bias was mainly attributable to the tablet shape.
This work was supported, in part, by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number JP17K08252.
The authors declare no conflict of interest.