擬似球としての樹幹表面

抄録

樹幹の根元の円盤の中心を原点とする。原点から垂直に高さzまで、さらにそこから水平に半径rの樹幹表面までとった直線を、S-S折線と名付ける。S-S折線上の2点間の隔たりを、樹幹がその区間を生長するに要する時間で距離づけることにすると、樹幹表面のすべての点は、原点から等距離にある。その意味で、樹幹表面は擬似球Qである。年齢tの擬似球の方程式は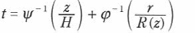

と書かれる。ここでH, R(z) は、それぞれ樹高と高さzでの半径生長の極限、またとは、それぞれ樹高と半径rの生長関数の逆関数である。
樹幹Qの一種の特性関数uを3変数t, z, r の関数として

で定義して、樹幹のHeaviside 関数と名付けると、uは線形同次一階の偏微分方程式

の“弱い解”となり、樹幹表面はその特性曲面となる。言い換えれば、解u = 1は樹幹表面で不連続に、u=0に飛躍する。したがって、樹幹表面は、樹幹生長に対して一種の波面前線と見做すことができる。