第4章　基準値

Abstract

臨床検査における「基準値」は，結果の解釈や判断を行う上での重要な指標である。基準値は，一般的に基準範囲や臨床判断値である病態識別値（カットオフ値），治療目標値，予防医学値など，さまざまな指標が含まれるあいまいな用語であることに注意する必要がある。本文では，基準範囲を設定する際の基本的な統計手法について解説する。基準範囲は，健常者の中から選ばれた基準個体の検査値分布の95%信頼区間を基に設定される。「基準個体」とは，健常者からその検査値に明瞭な影響を与える状態（生理的変動因子）や病態を有する個体を可能な限り除外した健常者のことである。一方，血中成分の一部は正規分布に近似するものもあるが，多くは正規分布から対数正規分布の間の分布を示すことから，基準値の設定に際しては，正規分布になるようにべき乗変換を施行し，その後に95%信頼区間を算出する。算出された信頼区間を基に逆変換を行うことによって基準範囲が設定される。

I　 確率紙を用いた基準値の導出

1． 基準範囲と病態識別値

臨床検査の結果を判断するための指標になる値として，基準範囲，病態識別値，治療目標値，カットオフ値がある。

1） 基準範囲

一定の基準を満たす健常人を基準個体（reference individual）として，測定値分布の中央から0.95（95%）が含まれる範囲から求められる。データの分布が正規分布であれば平均値 ± 1.96 SDとなるが，正規分布を示さない場合には，後述するべき乗変換を用いて正規化を行い95%の範囲を算出する¹⁾。したがって，データの分布型からどのようにデータを処理するかを判断する必要がある。多くの検査項目では正規分布を示さないため，べき乗変換により正規化を行ってから算出することが多い。

ところで，基準範囲を求める際の「健常人」に対する明確な定義がないという問題もある。一般的には，その時点で治療中の病気がなく，投薬を受けていないこと，肥満や痩せていないこと（これ自体も明確な定義はない），生活習慣として喫煙や飲酒，検査データとしては貧血や極端な異常値がないことなどが条件となる。後述のJCCLS共用基準範囲²⁾では，以下の除外基準に該当しないものを基準個体の候補者として募集基準が設けられ実施している。

除外基準

・BMI ≥ 28

・飲酒量（エタノール換算） ≥ 75 g/日

・喫煙 > 20本／日

・定期的な薬物治療

・妊娠中または分娩後1年以内

・術後，急性疾患で入院後2週以内

・HBV，HCV，HIVのキャリア

2） 病態識別値

専門学会などが設定するもので，ある疾患に罹っている患者の結果を分析して，疾患と検査の関係を感度と特異度またはROC曲線（receiver operating characteristic curve）などのデータから算出するものである。例えば尿酸値の共用基準範囲の上限値は男性で7.8 mg/dLであるが，高尿酸血症・痛風の治療ガイドラインでは，尿酸値が7.0 mg/dLを超えると痛風の危険性が増すことから，上限値は7.0 mg/dLに設定している。

3） 治療目標値

病態識別値の他に，専門学会で危険因子の状況によって治療目標値を設定している項目もある。例えば，高血圧治療で達成しなくてはならない治療目標の血圧値として140/90 mmHg未満などがある。

4） JCCLS（日本臨床検査標準協議会）の共用基準範囲

生化学・血液・一部免疫の項目の全40項目については，3種類の大規模な基準個体検査値データ（日本臨床衛生検査技師会³⁾，IFCC 市原プロジェクト^4),5)，福岡県五病院会⁶⁾）をもとに作成されたJCCLS共用基準範囲があり，採用する施設も徐々に増加している。

II　 分布型の観察方法

1． 分布型

統計学は，バラツキを伴う情報を客観的に分析・評価する学問であるため，分析したい集団の分布型を分析することが第一歩である。データの特徴をつかむには，度数分布図（ヒストグラム）を作って視覚的にとらえることが大切である。

2． 分布特性の観察

データがどのような分布を示しているのか，5つのポイントを観察する。特に単峰性か多峰性か，飛び離れ値の存在をチェックすることが重要で，これらの存在を知らずに統計処理を進めると異なる母集団を同一のものとして処理してしまう可能性が高い。

データのチェックポイント

・分布の中心（平均値・中央値・最頻値）

・分布の範囲，バラツキ方

・分布の歪み，尖り

・単峰性か，多峰性か

・飛び離れ値の存在

3． ヒストグラムの作り方

①最大値と最小値を選択する。

②階級の数およびクラスの幅を決める。

③階級の数は7～15程度にするのが一般的で，奇数値を用いる。奇数値を用いるのは，ピーク値を分かりやすくするためである。

④きりの良い数字で分かりやすくするのも重要である

階級数を決定する目安としてStargesの公式があるが，分布の形（極端値がある場合など）によって調整することもある（n：データ数）。

$階級数k={log}_{2}n+1$ （Table 1）

Table 1　Stargesの公式による階級数の目安

データ数	16	32	64	128	256	512	1,024
階級数	5	6	7	8	9	10	11

4． 分布の形状を表す指標

1） 歪度（skewness）

正規分布から左右にどの程度逸脱しているかをみる指標で，分布の非対称度を表す。正の値をとれば右の方に歪んだ分布，負の値をとれば左の方に歪んだ分布，0ならば左右対称である（Figure 1）。

Figure 1　 歪度の模式図

b₁ > 0右裾広がりの分布

b₁ = 0正規分布

b₁ < 0左裾広がりの分布

  

$$b_1=\sqrt{n}\frac{\sum _{}^{}{(x_i-\overline{x})}^3}{{\left(\sum _{}^{}{(x_i-\overline{x})}^2\right)}^{3/2}}=\frac{1}{n}\sum _{i=1}^n{\left(\frac{x_i-\overline{x}}{s}\right)}^3$$

2） 尖度（kurtosis）

正規分布からどの程度ピークが鋭いかをみる指標で，分布の尖り具合と裾の長さを表す。正の値をとれば広がった分布，負の値をとれば尖った分布。0 ならば正規分布と判断する（Figure 2）。

Figure 2　 尖度の模式図

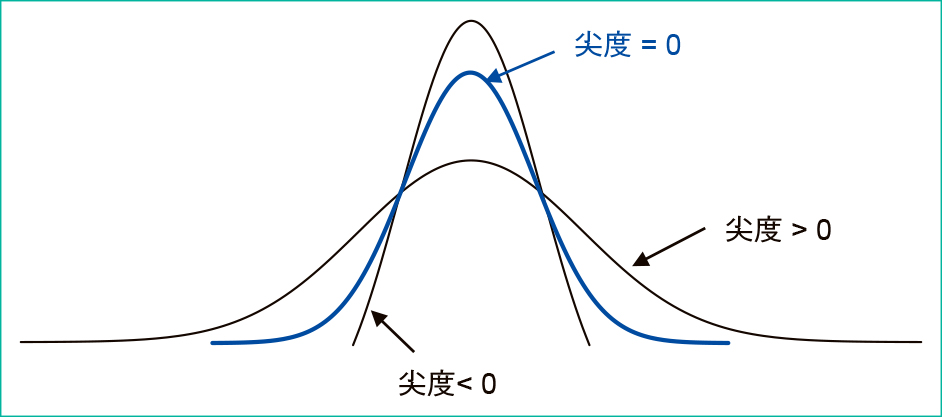
歪度・尖度は，データ数が30以下の時にはあてにならない。データ数が少ない場合には，これまでの資料データもしくは経験的に正規分布かどうか判定する。

b₁ > 0 裾広がりの強い分布

b₁ = 0 正規分布

b₁ < 0 裾が途切れた分布

  

$$b_1=n\frac{\sum _{}^{}{(x_i-\overline{x})}^4}{{\left(\sum _{}^{}{(x_i-\overline{x})}^2\right)}^2}-3=\frac{1}{n}\sum _{i=1}^n{\left(\frac{x_i-\overline{x}}{s}\right)}^4-3$$

5． 正規確率紙によるデータの分布状況の確認

統計的手法の多くは，正規分布を前提としているので，データが正規分布であることを確認することは重要である。正規確率紙は，データの分布状況を把握するうえで，ヒストグラム以上に分かりやすいものである^9)～11)。正規確率紙は，横軸に一様な目盛り，縦軸が正規確率目盛りを持つグラフ用紙のことである。測定した標本データを正規確率紙上にプロットするだけで，正規分布になっているかどうか容易に判断でき，正規分布の場合には標準偏差や95%信頼区間などを知ることができる。以下に，正規確率紙上のデータの判定方法と各分布の代表例として総コレステロール（T-cho），ALT，髄液中Cl，のヒストグラムおよび正規確率紙上プロットデータを示す。

1） 正規確率紙を用いた正規分布判定

・直線を示すもの：正規分布（Figure 3）

Figure 3　 健常者のT-cho分布

正規分布では，正規確率紙上のグラフは直線を示す。平均値 ± 95%の範囲も容易に読み取れる。

・上に凸の曲線：右裾広がりの分布（Figure 4）

（臨床検査のデータでは，この分布型を示すものが多い）対応方法は，べき乗0 ≤ p < 1で正規化後解析を行う。

Figure 4　 健常者のALT分布

ヒストグラムで右裾広がりの分布示すALTでは，正規確率紙上のグラフは上に凸の曲線を描いている。

・下に凸の曲線：左裾広がりの分布（Figure 5）（べき乗1 < pで正規化後解析を行う）

Figure 5　 髄液中Clの分布

左裾広がりの分布では，下に凸の曲線が描かれる。

III　 分布型のべき乗変換

1． 代表的な臨床検査データのヒストグラムによる分布型

主な臨床検査の中で，正規分布に近いものは赤血球，ヘモグロビン，電解質（Na, IP），総タンパク，アルブミンであり⁶⁾，尿酸，クレアチニンになると歪みがあり，中性脂肪（TG），GGTではほぼ対数正規分布型を示す。

2． べき乗変換（対数変換）による正規化

歪みのある項目や対数正規分布型の検査項目では，Box-Coxのべき乗変換式を用いることで正規分布に近似する分布に変換することができる^9)～12)。Box-Coxのべき乗変換式は，以下に示す式であり，べき乗変換（対数変換）による正規化例をFigure 6④に示す。高度に歪みのあるデータが正規分布に近似していることがわかる。

Figure 6　 各種臨床データのヒストグラムとべき乗変換（対数変換）による正規化例

Box-Coxのべき乗変換式

  

$$X=\{\begin{array}{c}\hfill \frac{{(x-a)}^p-1}{p}\leftarrow p\ne 0\\ \hfill log(x-a)\leftarrow p=0\end{array}$$

xは個々のデータであり，pはべき乗値を示し，aは変換原点を表す。変換原点aは，得られたデータの最小値よりも少し小さい値で，aを指定することでより正規分布に近づけることができる。

正規分布に変換した後は，両側2.5%領域をカットした範囲をもって基準範囲のポイントとし，逆変換によって元のデータに再変換して基準範囲とする^7),12)。

COI開示

本論文に関連し，開示すべきCOI 状態にある企業等はありません。

文献

• 1)   市原  清志：潜在基準値法による日常検査情報の活用．臨床検査，2005; 49: 1471–1485.
• 2)  日本臨床検査標準化協議会　基準範囲共用化委員会（編）：日本における主要な臨床検査項目の共用基準範囲案―解説と利用の手引き―，2022．https://www.jccls.org/wp-content/uploads/2022/10/kijyunhani20221031.pdf （2023年2月23日アクセス）
• 3)   Yamamoto  Y et al.: Nationwide multicenter study aimed at the establishment of common reference intervals for standardized clinical laboratory tests in Japan. Clin Chem Lab Med, 2013; 51: 1663–1672.
• 4)   Ichihara  K et al.: The Asian project for collaborative derivation of reference intervals: (1) strategy and major results of standardized analytes. Clin Chem Lab Med, 2013; 51: 1429–1442.
• 5)   Ichihara  K et al.: The Asian project for collaborative derivation of reference intervals: (2) results of non-standardized analytes and transference of reference intervals to the participating laboratories on the basis of cross-comparison of test results. Clin Chem Lab Med, 2013; 51: 1443–1457.
• 6)   Kinoshita  S et al.: Standardization of laboratory data and establishment of reference intervals in the fukuoka prefecture: A Japanese perspective. CIin Chem Lab Med, 2001; 39: 256–262.
• 7)   Ichihara  K,  Boyd  J: An appraisal of statistical procedures used in derivation of reference intervals. Clin Chem Lab Med, 2010; 48: 1537–1551.
• 8)   細萱  茂実：基準範囲の決め方．検査と技術，2008; 36: 151–155.
• 9)   市原  清志：バイオサイエンスの統計学，南江堂，東京，1990.
• 10)   佐藤  正一：病院で使える「臨床統計解析」，東広社，東京，2009.
• 11)   市原  清志， 佐藤  正一， 山下  哲平：〈新版〉統計学の基礎（第2版）日本教育研究センター，大阪，2016.
• 12)   佐藤  正一， 市原  清志：なぜ正常範囲ではなく“基準範囲”なのか．Medicina, 2020; 57: 827–831.