モデルの適用範囲の考慮したアンサンブル学習法の開発

Abstract

定量的構造活性相関や定量的構造物性相関では，それぞれ化合物の活性・物性 y と化学構造の特徴を数値した分子記述子 x との間の関係を定量的にモデル化する．回帰モデルの予測性能を向上させるため，アンサンブル学習では複数のサブモデルを構築し，サブモデルからの y の予測値を統合して最終的な y の予測値を計算する．各サブモデルの適用範囲 (applicability domain, AD) を考慮することで，AD 内のサブモデルのみ用いてアンサンブル学習における予測性能が向上することは確認されているが，x が異なるサブデータセット間で AD の比較はできず，新しいサンプルごとにサブモデルを選択したり重み付けしたりして y の値を予測することはできなかった．そこで本研究では AD の指標の 1 つである similarity-weighted root-mean-square distance (wRMSD) に着目し，wRMSD に基づいてサブモデルの重み付けを行う wRMSD-based AD considering ensemble learning (WEL) を開発した．wRMSD は y のスケールであるため x の異なるサブモデル間で AD の比較ができ，wRMSD に基づいて各サブモデルからの y の予測値に重み付けすることで，予測値の信頼性の高いサブモデルほど重みを大きくして予測することが可能となる．水溶解度・毒性・薬理活性それぞれが測定された 3 つの化合物データセットを用いた解析をしたところ，WEL を用いることで従来のアンサンブル学習法と比較して AD が広がり予測性能が向上することを確認した．WEL の Python コードは https://github.com/hkaneko1985/wel から利用可能である．

1 はじめに

定量的構造活性相関 (quantitative structure-activity relationship, QSAR) [1] や定量的構造物性相関 ((quantitative structure-property relationship, QSAR) [2] では，それぞれ化合物の活性・物性 y と化学構造の特徴を数値した分子記述子 x との間の関係を定量的にモデル化する．既知の化合物群からこれらの関係を回帰モデルとすることで，y の値が未知の化学構造において，それを合成したあとに発現すると考えられる y の値を予測できる．

あらゆる化学構造をモデルに入力できることが理想であるが，モデルの構築に用いた化合物の化学構造と大きく異なる化学構造の y の値を予測する場合，予測誤差が大きくなってしまう．QSAR, QSPR では新たな化学構造における予測値の信頼性を評価するため，モデルの適用範囲 (applicability domain, AD) [3, 4] を考える必要がある．AD とはモデルが本来の予測性能を発揮できる x の領域のことである．ある領域内における予測値の信頼性を評価することで，その領域内の化学構造の予測誤差の範囲を見積もることができる．

AD の設定方法として，主にデータ密度 [5] とアンサンブル学習法 [6] が挙げられる．データ密度の例として k 最近傍法 [7] では，ある化学構造とそれに最も近い k 個のモデル構築用の化合物における化学構造との間における x の空間での距離の平均を AD の指標とする．この指標の値が小さいほど，予測誤差は小さいと考えられる．One-class support vector machine (OCSVM) [8] はクラス分類手法の 1 つである support vector machine [9] を領域推定問題に応用した手法であり，OCSVM によりデータ密度の高い領域を推定できる．

アンサンブル学習では複数のサブモデルによる予測値の標準偏差を AD の指標とする．サブモデルとは，データセットのサンプルや x をランダムに選択して得られたサブデータセットを用いて構築されたモデルである．ある化学構造の y の値を予測する場合，サブモデルの数だけ予測値が得られ，そのばらつきの指標である標準偏差により予測誤差を見積もる．

アンサンブル学習では各サブモデルの予測値の平均値を，最終的な y の予測値とする．Random forests [10], XGBoost [11], LightGBM [12] のように，アンサンブル学習により単一のモデルの予測性能と比較して，予測性能を向上させることが可能である．

アンサンブル学習におけるサブモデルも 1 つのモデルであり，AD を定義できる．サブモデルの AD を考慮して，ある化学構造における y の値を推定する際に AD 内のサブモデルのみ使用することで，AD が広がり予測性能が向上することが確認された [13]．しかし，y の値を予測したい化学構造ごとに，使用するサブモデルを選択したりサブモデルに重み付けをしたりすることを自動的に行うことはできなかった．

本研究では，サブモデルの AD を考慮したアンサンブル学習法を開発することを目的とした．サブモデルを選択したりサブモデルに重み付けしたりするためには，AD を定量的に評価してサブモデル間の AD を比較する必要がある．データ密度はサンプル間の距離に基づくため，x をランダムに選択してサブデータセットを作成し，それを用いてサブモデルを構築した場合，各サブモデルの AD を設定するために計算される距離は，x が異なるためサブモデル間で比較できない．そこで本研究では AD の指標の 1 つである similarity-weighted root-mean-square distance (wRMSD) [14] に着目した．wRMSD はk 個の最も近いモデル構築用のサンプルの誤差に基づく指標であり，値が小さいほど予測値の信頼性は高い．wRMSD のスケールは y のスケールと同じであるため，アンサンブル学習においてサブモデルごとに wRMSD を計算してもサブモデル間で AD を比較することが可能となる．

提案手法を wRMSD-based AD considering ensemble learning (WEL) と呼ぶ．ある化学構造の y の値を推定する場合，各サブデータセット・サブモデルにより x の値から y の予測値と wRMSD の値を計算する．wRMSD の値の逆数に応じた重みで重み付き平均した予測値を最終的な y の予測値とする．x の値から計算される wRMSD の値が小さいサブモデルほどに予測値の信頼性は高いと考えられ，その予測値の重みを大きくすることで，精度良く y の値を予測できると考えられる．

本手法の有効性を検証するため，水溶解度・毒性・薬理活性それぞれが測定された 3 つの化合物データセットを用いた解析を行う．回帰分析手法の一つである partial least squares regression (PLS) [15] を対象にして，PLS, ensemble PLS (EPLS)，提案手法と PLS とを組み合わせた WEL-PLS で比較検討を行う．

2 手法

WEL では各サブモデルの AD を統合するための指標として wRMSD [14] を用いる．あるサンプルの y の値を予測する際，i 番目のサブモデルにおける wRMSD の値 wRMSD_i は以下のように計算できる．   

$wRMS{D}_i=\sqrt{\frac{\sum _{j=1}^k{\left(w^{\left(j\right)}\right)}^2{\left(y_i^{\left(j\right)}-y_{\text{pred},i}\right)}^2}{\sum _{j=1}^k{\left(w^{\left(j\right)}\right)}^2}}$(1)

ここで k は最近傍サンプルの数，y_i^(j) は i 番目のサブデータセットにおける j 番目の近傍サンプルの y の実測値，y_pred,i は i 番目のサブモデルで予測された y の値である．w_i^(j) は以下のように計算できる．   

$w_i^{\left(j\right)}=\frac{1}{D_i^{\left(j\right)}+0.5}$(2)

ここで D_i^(j) は以下のように計算される．   

$D_i^{\left(j\right)}=\sum _{p=1}^m\min \left(\frac{\left|x_{i,p}^{\left(j\right)}-x_p\right|}{5{\sigma }_{i,p}},1\right)$(3)

m は記述子の数，x_i,p^(j) は i 番目のサブデータセットにおける j 番目の近傍サンプルの p 番目の x の値，x_p は予測用サンプルの p 番目の x の値，σ_i,p は i 番目のサブデータセットにおける p 番目の x の標準偏差である．wRMSD_i は i 番目のサブモデルにおける予測用サンプルの予測値の信頼性を表し，値が小さいほど信頼性は高い．

Figure 1 に提案手法 WEL の概念図を示す．モデル構築時にはx をランダムに選択して n 個のサブデータセットを作成し，サブデータセットごとに回帰分析手法でサブモデルを構築する．予測用サンプル (Figure 1 の Query sample) における y の値を予測する際は，サブモデルごとに y の予測値 y_pred,i と wRMSD_i を計算する．そして以下の式により最終的な y の予測値 y_pred を計算する．   

$y_{\text{pred}}=\sum _{i=1}^n{z}_i{y}_{\text{pred},i}$(4)

z_i は各サブモデルの重みであり，以下の式により計算される．   

$z_i=\frac{{\left(\frac{1}{wRMS{D}_i}\right)}^r}{\sum _{j=1}^n{\left(\frac{1}{wRMS{D}_j}\right)}^r}$(5)

式(5) により wRMSD の値が小さいほど y の予測値に対する重みが大きくなり，予測用サンプルごとに AD 内で y の予測値の信頼性が高いサブモデルほど重みを大きくすることができる．

Figure 1.

 Basic concept of the proposed method WEL

r の値はクロスバリデーションにより最適化する．

WEL の Python コードは https://github.com/hkaneko1985/wel から利用可能である．

3 結果と考察

提案手法の有効性を検証するため 3 つのデータセットを使用した．1 つ目は水溶解度のデータセット solubility [16] であり，水溶解度が測定された 1290 個の化合物である．y は水への溶解度を S [mol/L] としたときの log(S) である．2 つ目は環境毒性のデータセット toxicity [17] であり，環境毒性が測定された 1213 個の化合物である．y は，ある時間に Tetrahymena pyriformis の増殖の 50% を阻害する化合物の濃度を IGC₅₀ [μM] としたときの −log(IGC₅₀)である．3つ目は薬理活性のデータセット activity [18] であり，アンジオテンシン変換酵素阻害薬として薬理活性が測定された 114 個の化合物である．y は，標的のタンパク質の 50% を阻害する化合物の濃度を IC₅₀ [μM] としたときの −log(IC₅₀) である．データセットごとのモデル構築用データのサンプル数とモデル検証用データのサンプル数を Table 1 に示す．一般的にはモデル構築用データのサンプル数は全体の 70% から 80% にするが，今回は AD が狭い状況におけるモデルの推定性能を検討するため，モデル構築用データのサンプル数を小さくした．

Table 1. The numbers of training samples and test samples for each dataset

	Training samples	Test samples
solubility	300	990
toxicity	100	1113
activity	50	64

x として RDKit [19] を用いて計算した 200 個の記述子を使用した．データセットごとに，8 割以上のサンプルで同じ値を持つ x は削除した．

回帰分析手法として PLS を用いて，PLS, ensemble PLS (EPLS), 提案手法と PLS とを組み合わせた WEL-PLS で比較検討を行った．PLS の Python コードとして scikit-learn [20] を利用した．EPLS, WEL-PLS におけるサブデータセットの数は 100 とし，記述子の数の 50% をランダムに選択することで作成した．WEL-PLS において k = 5 とした．PLS における成分数の最大数を 30，WEL-PLS における r の候補を 0.5, 1,…, 9.5, 10 として，それぞれ 5-fold クロスバリデーション後の決定係数 r² が最大となる値を採用した．

solubility, toxicity, activity において，モデル構築用データを用いた 5-fold クロスバリデーションにより最適化された WEL-PLS の r は，それぞれ 2.5, 3, 8 であった．

solubility, toxicity, activity それぞれのデータセットを用いた場合における，PLS, EPLS, WEL-PLS でモデル構築用データを予測したときの r² および root-mean-squared error (RMSE) の値をそれぞれ Tables 2, 3, 4 に示す．RMSE は予測誤差の二乗和の平均値を 0.5 乗したものであり，値が小さいほどモデルの予測性能が高いことを表す．さらに Figures 2, 3, 4 にそれぞれ Tables 2, 3, 4 に対応する y の実測値と予測値とのプロットを示す．Tables 2, 3 より，solubility のデータセットや toxicity のデータセットを用いた場合に，PLS や EPLS では r² の値が 0 を下回っていることが分かる．対応する Figures 2, 3 のプロットより，対角線から大きく外れたサンプルが散見され，これらが r² の小さい原因であると考えられる．このような状況において WEL-PLS を用いることで，r² は向上して 0 を上回り，RMSE の値は PLS や EPLS の RMSE の値と比較して小さく，提案手法によりモデルの予測性能が向上することを確認した．Figures 2, 3 のプロットを見ても，WEL-PLS では PLS や EPLS のように対角線から大きく外れたサンプルは存在せず，すべてのサンプルにおいて良好に y の値を予測できたことがわかる．PLS や EPLS において対角線から外れたサンプルは，モデル検証用データにおける x の値がモデル構築用データにおける記述子の値から離れたサンプルであり，WEL-PLS を用いることでそのような x が選択されたサブモデルの重みを小さくすることで，外れ値の影響を受けず安定的に予測できたと考えられる．これは PLS モデルや EPLS モデルの AD と比較して WEL-PLS のAD が広いことを意味している．提案手法を用いることで，従来手法で構築されたモデルより AD が広がり，多くのサンプルを精度良く予測できることを確認した．

Table 2. r² and RMSE of test samples for each method for solubility dataset

	r2	RMSE
PLS	-66.9	16.7
EPLS	-15.9	8.33
WEL-PLS	0.884	0.690

Table 3. r² and RMSE of test samples for each method for toxicity dataset

	r2	RMSE
PLS	-2.46	1.99
EPLS	-0.640	1.37
WEL-PLS	0.626	0.653

Figure 2.

 Actual y vs. predicted y plot for each method for solubility dataset

Figure 3.

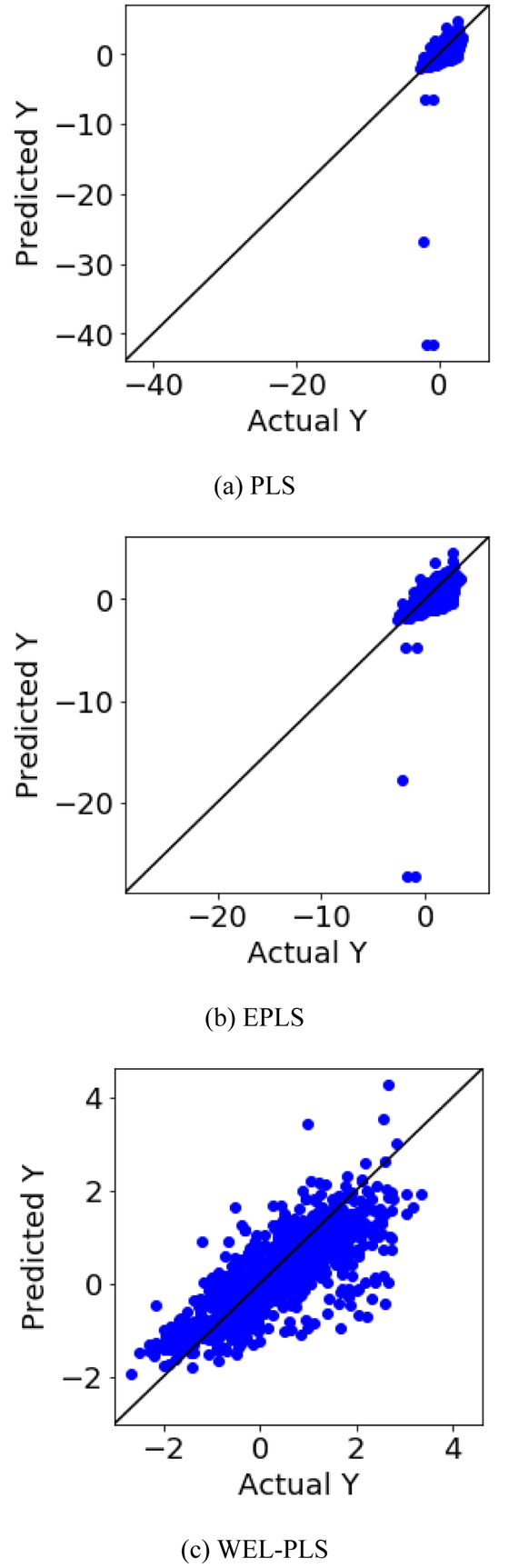
 Actual y vs. predicted y plot for each method for toxicity dataset

Table 4 より activity のデータセットを用いた場合も，PLS や EPLS と比較して WEL-PLS の r² の値が大きく，RMSE の値が小さいことから，提案手法を用いることでモデルの予測精度が向上することを確認した．Figure 4 の実測値と予測値とのプロットより，PLS, EPLS と比較して，WEL-PLS では y の値が大きい高活性の化合物における予測誤差が小さかった．構築したモデルを化学構造設計に応用する場合，高い活性をもつと考えられる化学構造を生成する必要があるため，高活性な化合物を精度良く予測できるモデルは望ましいといえる．

Table 4. r² and RMSE of test samples for each method for activity dataset

	r2	RMSE
PLS	0.593	1.48
EPLS	0.614	1.44
WEL-PLS	0.682	1.31

Figure 4.

 Actual y vs. predicted y plot for each method for activity dataset

提案手法を用いることで従来手法と比較して AD が広がり y の予測精度が向上することを確認した．

4 結言

本研究ではアンサンブル学習により回帰モデルを構築する際に，各サブモデルの AD を考慮した手法 WEL を開発した．AD の指標の一つである wRMSD に基づく各サブモデルの重みを提案し，最終的な y の予測値は各サブモデルの予測値の重み付き平均で与えられる．提案手法によりサンプルごとに AD 内で予測値の信頼性が高いサブモデルほど重みを大きくして y の値を予測することが可能となる．

QSAR, QSPR に関連する 3 つのデータセットを用いて提案手法と PLS とを組み合わせた手法の有効性を検証したところ，すべてのデータセットにおいて既存の PLS モデルや EPLS モデルより予測精度が向上することを確認した．さらに，モデルの AD が広がり多くのサンプルを小さい誤差で予測できるようになった．

提案手法により QSAR, QSPR 研究が促進することを期待する．

謝辞

本研究は，JST，COI若手連携研究ファンド，R1WD12の支援を受けたものである．

参考文献

• [1]   A. Tropsha, Mol. Inform., 29, 476 (2010). ,doi:10.1002/minf.20100006127463326
• [2]   S. Sahoo, C. Adhikari, M. Kuanar, B. Mishra, Curr. Computeraided Drug Des., 12, 181 (2016). , doi:10.2174/157340991266616052511211427222031
• [3]   I. V. Tetko, I. Sushko, A. K. Pandey, H. Zhu, A. Tropsha, E. Papa, T. Öberg, R. Todeschini, D. Fourches, A. Varnek, J. Chem. Inf. Model., 48, 1733 (2008). , doi:10.1021/ci800151m18729318
• [4]   D. Horvath, G. Marcou, A. Varnek, J. Chem. Inf. Model., 49, 1762 (2009). , doi:10.1021/ci900057919530661
• [5]   I. I. Baskin, N. Kireeva, A. Varnek, Mol. Inform., 29, 581 (2010). , doi:10.1002/minf.20100006327463453
• [6]   I. Sushko, S. Novotarskyi, R. Körner, A. K. Pandey, A. Cherkasov, J. Li, P. Gramatica, K. Hansen, T. Schroeter, K. R. Müller, L. Xi, H. Liu, X. Yao, T. Öberg, F. Hormozdiari, P. Dao, C. Sahinalp, R. Todeschini, P. Polishchuk, A. Artemenko, V. Kuz’min, T. M. Martin, D. M. Young, D. Fourches, E. Muratov, A. Tropsha, I. Baskin, D. Horvath, G. Marcou, C. Muller, A. Varnek, V. V. Prokopenko, I. V. Tetko, J. Chem. Inf. Model., 50, 2094 (2010). , doi:10.1021/ci100253r21033656
• [7]   R. P. Sheridan, B. P. Feuston, V. N. Maiorov, S. K. Kearsley, J. Chem. Inf. Comput. Sci., 44, 1912 (2004). , doi:10.1021/ci049782w15554660
• [8]   Y. Xiao, H. Wang, W. Xu, J. Zhou, Chemom. Intell. Lab. Syst., 151, 15 (2016). .doi:10.1016/j.chemolab.2015.11.010
• [9]   C. M. Bishop, Pattern Recognition and Machine Learning, Springer, New York (2006).
• [10]   D. S. Palmer, N. M. O’Boyle, R. C. Glen, J. B. O. Mitchell, J. Chem. Inf. Model., 47, 150 (2007). , doi:10.1021/ci060164k17238260
• [11]   T. Chen, C. Guestrin, arXiv:1603.02754 (2016).
• [12]   G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye, T. Y. Liu, NIPS Proceedings, (2017).
• [13]   H. Kaneko, J. Chem. Inf. Model., 58, 480 (2018). , doi:10.1021/acs.jcim.7b0064929425038
• [14]   C. E. Keefer, G. W. Kauffman, R. R. Gupta, J. Chem. Inf. Model., 53, 368 (2013). , doi:10.1021/ci300554t23343412
• [15]   S. Wold, M. Sjöström, L. Eriksson, Chemom. Intell. Lab. Syst., 58, 109 (2001). .doi:10.1016/S0169-7439(01)00155-1
• [16]   T. J. Hou, K. Xia, W. Zhang, X. J. Xu, J. Chem. Inf. Comput. Sci., 44, 266 (2004). , doi:10.1021/ci034184n14741036
• [17]   http://www.cadaster.eu/node/65.html.
• [18]   J. J. Sutherland, L. A. O’Brien, D. F. Weaver, J. Med. Chem., 47, 5541 (2004). , doi:10.1021/jm049714115481990
• [19]   https://www.rdkit.org/
• [20]   https://scikit-learn.org/stable/