水素原子がふたつ集まって水素分子をつくる過程を原子価結合法や分子軌道法で取り扱うと,分子を形成した方が安定になることを説明できる.このとき,分子軌道における原子軌道の波の重なり方が同じ位相のときは安定な結合性分子軌道が出来,異なる位相のときは不安定な反結合性分子軌道が出来る.
In 1811, A. Avogadro explained that elementary hydrogen exists as H2 molecules. Avogadro's findings were almost completely ignored until S. Canizarro presented them at the Karlsruhe Conference in 1860. In 1916, G. N. Lewis described the sharing of electron pairs between atoms. This idea provides a picture of covalent bonding, however, quantum mechanics is needed to understand the nature of the chemical bond. In 1927, W. Heitler and F. London were succeeded in the first explanation of the chemical bond of molecular hydrogen based on the valence bond method. Molecular orbital (MO) method was also proposed to explain theoretically the nature of the chemical bond. Similar to photons, electrons show properties of particles and waves. A. Tonomura revealed that the wave character of electron is displayed when a beam of electron is passed through parallel slits thereby creating interference patterns [5, 7, 8]. Formation of two molecular orbitals φ1 (bonding MO) and φ2 (antibonding MO) from the interference of two hydrogen atomic orbitals χ1 and χ2 is shown in Figure 4. Electron density distribution in the 3-dimensional representation of the squares of hydrogen MOs are given in Figure 5. Difference electron density between |φ1|2 and (|χ1|2 + |χ2|2) in Figure 6 (c) and 7 (b) shows the internuclear region having high probability densities of finding an electron, to explain electron densities (-δe) in this region could attract the hydrogen nuclei having plus electric charges.
前々回,水素原子の原子軌道を波動性という観点で整理し,どのような規則性があるかを力学的な振動とも対比させて調べた [1].今回は,原子から分子を生ずるときに,原子軌道の波の重ね合わせの考え方がどのように重要かという観点で調べる.
1700年代の後半,水素,窒素,酸素などの単体が相次いで発見された.1808年,ドルトンは,「化学哲学の新体系」という著書を刊行し,これ以上分割できないものとして,原子が存在すると論じた.ドルトンの原子説は革新的であったが,単体と元素を同一とする誤りを含んでいた.現在では分子とされる水素(H2)などを原子と考えたために,原子量の計算値に不都合を生じていたのである [2 (a)].1809年,ゲイ・リュサックは,気体のみが関与する化学反応における各気体の体積比は簡単な整数比をなすという「気体反応の法則」を見出した.アボガドロは, 1811年,「同温同圧のもとでは,全ての気体は同じ体積中に同数の分子を含む」という法則を発表した.ドルトンは一種類の元素からなる気体は原子から構成されると主張した.この主張はさまざまな実験事実を説明できたが,気体同士の反応については説明できなかった.たとえば,水素2容積と酸素1容積を化合させると必ず水蒸気2容積となる.ドルトンの主張に従って,この反応を現代風に記述すると,式 (1) のように,分割できないはずの酸素原子が,生成する水蒸気のなかに半分ずつ含まれるという矛盾を生じる. 2H + O → 2HO1/2 (1)
アボガドロは,反応にあずかる気体は原子ではなく,同種の原子が2つ結合した分子からなると考えると,式 (2) のように正しい反応式が導けると主張した. 2H2 + O2 → 2H2O (2)
私たちは,式 (2) の方が正しいことを当たり前のように理解している.しかし,この正しい主張は容易に受け入れられなかった.「中性の原子が2つ集まって,たとえば,H2という分子になるのはどうしてか」という疑問に,誰も答えられなかったためである [3 (a)].
アボガドロの死後しばらく経った1860年にカールスルーエで開催された化学者会議で,カニッツァロは,アボガドロの主張の重要性を強調する講演をおこなった.ドルトンの理論では原子量が正しく求められないが,アボガドロの理論では是正されるという主張であった.メンデレーエフは,この講演に感銘を受け,周期表の発見に関する論文を発表するに至った.1916年にはルイスの電子対共有結合の概念も提出され,アボガドロの理論の重要性が次第に受け入れられるようになってきたのである.1927年,ハイトラーとロンドンは,水素分子(H2)が2つの水素原子(2H)よりも安定であることを,量子力学に基づく計算によって証明した [4].アボガドロが分子仮説を提出してから100年以上も経ってから,その正しさが立証されたのである.分子の安定化エネルギーや原子間距離,結合角などを求める方法としては,原子価結合法や分子軌道法がある.ハイトラーらは,前者の原型ともいえる方法でこれらを算出した.現在では,後者による方法が一般的で,手軽に入手できるプログラムを用いて水素分子の安定性を計算することが出来る [2 (b), (c)].
1800年代のはじめ頃,ヤングは,光が波であることを実験で示した.Figure 1 は,ヤングの実験をコンピューターでシミュレートしたものである [3 (b)].左図は,単スリットの実験である.位相のそろった波長 λ の光を幅 Δy の 1 つのスリットに通すと,充分な距離 l だけ離れたスクリーン上に干渉縞が観察される.縞のもっとも明るい点と最初の暗部との距離を y とすると,式 (3) の関係がある.
| (3) |
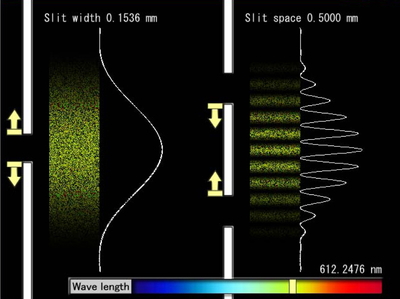
Simulation of Young's interference experiment. left: single slit, right: double slit. Slit width, slit space, and wavelength of monochromatic light are variable in this simulation.
式 (3) に Figure 1 左図のデータを代入し,スクリーンまでの距離 l = 7.5 m として計算すると,y はおよそ 3 cm と求められる.図ではスリット幅 Δy(左図の↑↓部分)を10倍くらいに拡大して示してある.シミュレーションでは,スリット幅 Δy を大きくすると,y は逆に小さくなることが確かめられる.
Figure 1 右図は,スリット間隔 Δd の2つのスリットを用いた実験である.それぞれのスリット幅は左図と同じなので,明るさのグラフの包絡線は左図と一致するが,より細分された干渉縞を与える.細分された暗部から次の暗部までの距離をdとすると次式 (4) の関係がある.
| (4) |
スリット間隔 Δd を大きくすると,干渉縞はより細分され,個々の縞模様の幅は逆に小さくなるのである.
ヤングは,これら2式を導くにあたり,回折で生じた2つの光の波の位相が同じ場合は Figure 2 (a) に示すように強め合って明るくなる干渉を引き起こし,2つの波の行路差が 1/2 波長ずれて異なる位相となる場合は Figure 2 (b) に示すように打ち消しあって,暗くなる干渉を引き起こすとした.つまり,この現象は,光が波であると考えて初めて説明できることを明らかにした.1905 年,アインシュタインは,光電効果の実験事実を説明するためには,光が粒子であると考えなければならないとし,これを光量子または光子 (photon) と呼ぶことを提唱した [3 (b)].光は波動性と粒子性のふたつの性質をあわせ持つことが明らかになったのである.
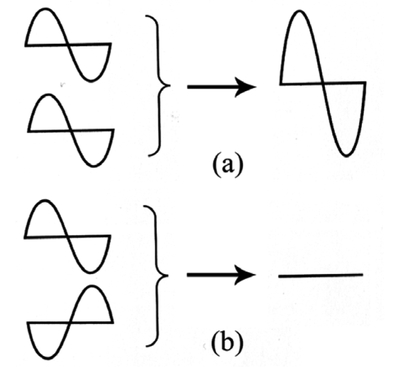
The interference of two waves. (a) When in-phase, the two waves create constructive interference. (b) When out-of-phase, they create destructive interference.
電子の発見は1897年,J. J. トムソンによってなされた.彼は,電子を粒子と考え,陰極線粒子と呼んだ.波動と考えられていた光が粒子性を持つならば,粒子と考えられていた電子が波動性を兼ね備えていてもおかしくはない.1924年,ド・ブロイは,このような発想から,物質の波動論を導いた.この考え方が正しいとすると,電子にも波の特徴である回折や干渉が観察されるはずである.1927年,G.. P. トムソンは,金の薄膜に電子線を照射し,回折環 (diffraction rings) が得られることを示した [5].
電子が波動性をもつことは本シリーズの第 1 回で,外村彰の実験として祥述した [6].彼は,波面のそろった電子線を二重スリットに通す装置を工夫し,光の場合と同じ干渉縞を,電子 1 個,1 個を逐次的に検出することより描くことに成功した [7, 8].その模様は,すでに示したように [5, Figure 3],最初はランダム(不確定)に見えるそのパターンが,電子の検出個数が増えるとともに,一定の干渉縞を与えるというものであった.このように,個々の電子を検出するときはあくまでも点状,つまり,粒子である.しかし,この粒子は,検出位置が不確定という意味で,粒子 1 個でも,波動性を秘めている.その不確定な位置の観測の繰り返しが,波の特徴である干渉縞を与えるからである.
ここで,前々回 [1] に述べた原子軌道,つまり,原子のなかの電子の状態を表す波動関数における波動性について復習しておこう.力学的な定常波における類推から,3 次元の波である原子軌道の断面は,2 次元の波である円形膜におこる定常波の特徴と対比できる.その一部をFigure 3 に再録した.Figure 3 (a), (b) は水素原子の 1s 軌道,2px 軌道の xy 平面による断面図である.(c-f) は,対応する円形膜の振動モードで,(c), (d) が見取図,(e), (f) が真上から見た図となっている.n, m は,それぞれ,動径接線(radial node)および方位接線(azimuthal node)の数である.原子軌道では無限遠の接線は数えないことになっているが,それも計算することにすると,(a, b) 図と(e, f) 図が見事に対応している.
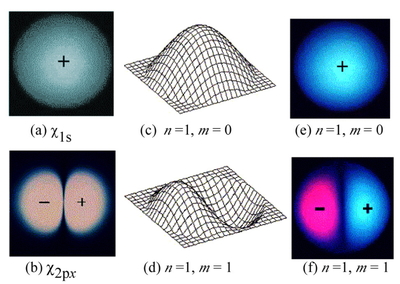
(a, b) Cross section on the x-y plane of 3-dimensional hydrogen atomic orbitals, (c − f) Characteristic pattern of standing waves of a 2-dimensional circular membrane of uniform thickness, attached to a rigid frame (n: number of radial nodes; m: number of azimuthal nodes)
分子軌道法において,2個の水素原子から水素分子が構築される様子を,Figure 4に模式的に示した.Ab initio法と呼ばれる分子軌道法 [9] で水素分子H2を取り扱うと,水素原子の2つの原子軌道χ1, χ2 から水素分子の2 つの分子軌道 φ1, φ2が次式のように求められる.
| (5) |
| (6) |
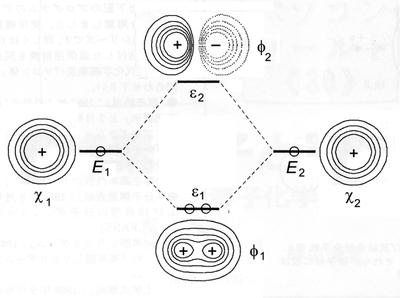
Formation of two molecular orbitals φ1 and φ2 from two hydrogen atomic orbitals χ1 and χ2 .
Figure 2 ですでに示したように,光の波の干渉では,同位相(位相が合ったとき,in-phase)では強め合い,異なる位相(out-of-phase)では打ち消し合う.上式において,φ1では 2 つの 波動 χ1とχ2 が同位相(同符号)で重なるので 2 つの波が分子の中央部で強め合う干渉を引き起こす.このとき,分子軌道 φ1のエネルギー ε1はもとの原子軌道χ1, χ2のエネルギー Eよりも低くなるため, φ1に電子が入ると(Figure 4の ε1 における○印)安定な結合が生成する.このため,φ1は結合性分子軌道と呼ばれる.
もうひとつの分子軌道 φ2では,2 つの 波動 χ1とχ2 が異なる位相(異符号)で重なるので 2 つの波が分子の中央部で打ち消し合う干渉を引き起こす.このとき,分子軌道 φ2のエネルギー ε2はもとの原子軌道 χ1, χ2のエネルギー E1, E2よりも高くなるため, Figure 4の ε1 に○印で示した 2 つの電子が φ2に移動すると,2 つの原子核を引き離す力が働いてしまう.そのため,φ2は反結合性分子軌道と呼ばれる.
水素原子の原子軌道 χ1, χ2 には,それぞれ 1 個の電子があったから,合計 2 個の電子を新しく生じた2つの分子軌道 φ1, φ2にエネルギーの低い順に 2個ずつ配置させると,Figure 4に示すように,φ1のみに2個の電子が詰まって満杯となり,φ2の方は空である.分子軌道において,電子が詰まった最もエネルギーの高い軌道を最高被占軌道(Highest Occupied Molecular Orbital, HOMO)といい,電子が空の最もエネルギーの低い軌道を最低空軌道(Lowest Unoccupied Molecular Orbital, LUMO)という.
Figure 5 (a) は,結合性分子軌道φ1(式(1))の平方と反結合性分子軌道φ2(式(2))の平方をガラス彫刻で表現したものである [2 (c), 10].これらは,Figure 4の中央の図(断面図)を3次元的に描いたものの平方であるから,図のかたちは同じで,ただ符号がすべて正符号になっている.
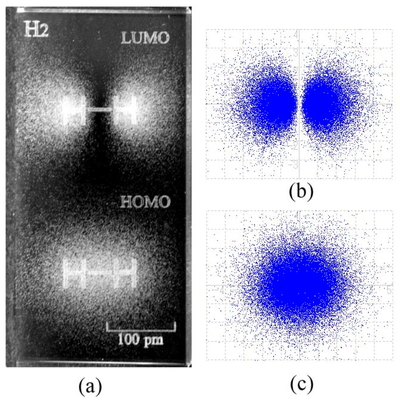
(a) Electron density distribution in the 3-dimensional representation of the squares of hydrogen molecular orbitals (MOs) engraved in a glass block (NEBULA [10]); top: antibonding MO |φ2|2, bottom: bonding MO |φ1|2. (b) Electron densities of antibonding MO |φ2|2, (c) bonding MO |φ1|2 projected on an x-y plane.
これまで何度も述べたように,軌道関数の平方は電子の存在確率(確率密度)を表す.Figure 5 (a) は,分子軌道φ1またはφ2の平方をガラス内に彫刻したもので,それぞれの軌道に電子1個が存在するとき,その1個の電子を3次元空間のどこに見出すかという確率密度を表している.彫刻された個々の点は,見出された電子を表しているから,点の密度の高いところは電子を見出す確率が高く,密度の低いところは確率が低いというわけである.点の集合は雲のように見えることから,電子雲という表現が使われることもある.電子は雲のように部分的にも質量を持った実体としては表現できない [1] ために確率で表すのであるが,電子雲という表現は,確率の雲といういささかあいまいな意味で便利につかわれている.電子を見出す確率密度を,電子密度と表現することがある.これは,電子を実在する雲に見立てた厳密には誤った表現であるが,やはり便利な表現という意味で,ひろくつかわれている [11].
Figure 5 (b) は,Figure 5 (a) 上図の反結合性分子軌道φ2(式(2))の平方 |φ2|2 ,つまり,電子密度を,分子軸を含む平面に投影したものである.Figure 5 (c) には,Figure 5 (a) 下図の結合性分子軌道 φ1(式(1))の平方としての電子密度|φ1|2 を,同様に投影した図が示してある.
Figure 6 (a) は,水素分子の分子軌道 φ1, φ2を導出する時に用いた平衡原子間距離に,水素原子 2 個を 配置できたと仮想したときの,原子軌道 χ1, χ2 をそれぞれ平方して計算した電子密度 |χ1|2 + |χ2|2 を同様に投影した図である.つまり,化学結合を生成する前の電子密度に相当する図である.Figure 5 (c) と Figure 6 (a) は,ほとんど同じ図のように見える.しかし,これらの差をとった関数 |φ1|2 − (|χ1|2 + |χ2|2)における電子を見出す確率を計算してみると,Figure 6 (c) のように,2つの水素原子核(青色)の間では電子密度が濃くなり(差が正,シアン色),それらの外側では電子密度が薄くなっている(差が負,ピンク色)ことがわかる.このように,特定の分子軌道の電子密度と結合前の原子軌道の電子密度の差を,差分電子密度と呼ぶ [12, 13].
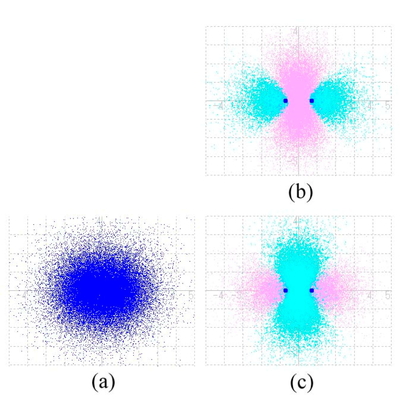
(a) Squares of two atomic orbitals |χ1|2 + |χ2|2. (b) Difference electron density |φ2|2 − (|χ1|2 + |χ2|2), (c) |φ1|2 − (|χ1|2 + |χ2|2).
一方,反結合性分子軌道の平方 |φ2|2(Figure 5 (b)) と 水素原子2個の平方の和 |χ1|2 + |χ2|2(Figure 6 (a)) の差分電子密度を Figure 6 (b) に示す.Figure 6 (c) とはほとんど逆になっていて,2つの水素原子核(青色)の間では電子密度が薄くなり(差が負,ピンク色),それらの外側では電子密度が濃くなっている(差が正,シアン色).
水素分子の結合性分子軌道に配置された電子は,水素原子核にどのような力を及ぼすのであろうか?その模様をFigure 7 (b) に示した.式 (1) に示したように,結合性分子軌道 φ1では,原子軌道 χ1, χ2 が同符号(同じ位相)で干渉するので,2 つの原子核の間の波が強めあう干渉を引き起こして電子密度が増大する.これを,Figure 7 (b) のシアン色の部分に-δeの記号で示した.ここで,eは電気素量(陽子の電荷)である.一方,2つの原子核(陽子)はそれぞれ +eの電荷を持つから,図に赤色の矢印で示すように,2つの原子核は引き寄せられて安定な分子を生成する [14, 15].この引き寄せる力を,結合力と呼ぶ [16].
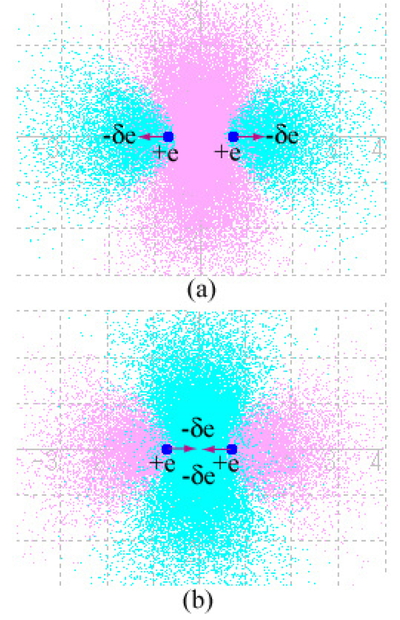
(a) The nuclei having +e electric charges are attracted to an accumulation of electron densities (-δe) outside the internuclear region in an antibonding orbital |φ2|2. (b) The nuclei (+e) are attracted to an accumulation of electron densities (-δe) in the internuclear region in a bonding orbital |φ1|2.
一方,反結合性軌道 φ2に仮に電子が配置されたとすると,電子密度の濃いところはFigure 5 (a) に示すように,原子核の外側に-δeで示したシアン色の領域となるから,赤色の矢印が逆向きとなり,2つの原子核を引き離す力(反結合力)がはたらく.
アボガドロが提唱した「水素は2原子分子である」という主張は,100年以上も後に,量子力学によってその正しさが理論的に明らかにされた.世の中には,量子力学を用いないと説明できない事象があり,この問題もそのひとつである.化学結合の主役は電子であり,原子軌道の干渉によって生じる結合性分子軌道において,負電荷を持つ電子の存在確率が高い核間の領域が,正電荷をもつ原子核同士を引き付ける"糊"のはたらきをしている.
「同温同圧のもとでは,全ての気体は同じ体積中に同数の分子を含む」というアボガドロの主張も,彼の生存中はその分子数が決められなかったが,アボガドロ数として大切な定数と称されるに至っている.各国において,10月23日を化学の日やモルの日などと称してイベントを行うことがしばしば見受けられる.アボガドロ数に因んだ月日の設定となっている.