ポリスチレン解重合のシミュレーション方法の検討

Abstract

To verify the possibility to simulate depolymerization, simulations of the depolymerization of polystyrene were performed. Molecular Dynamics simulations (MD) using neural network potentials were found to be similar in accuracy to MD using density functional theory calculations. It was also found that long-time simulations using neural network potential-MD predicted styrene monomer yields close to those obtained experimentally, and that the monomer yields tended to decrease with increasing pressure.

Translated Abstract

To verify the possibility to simulate depolymerization, simulations of the depolymerization of polystyrene were performed. Molecular Dynamics simulations (MD) using neural network potentials were found to be similar in accuracy to MD using density functional theory calculations. It was also found that long-time simulations using neural network potential-MD predicted styrene monomer yields close to those obtained experimentally, and that the monomer yields tended to decrease with increasing pressure.

1 序論

これまでの材料分野における産業界での研究では，材料を「組み立てる」ことに主眼を置いてきた．しかし，資源の枯渇により，自然から得た資源を消費するだけの産業が成り立たなくなると考えられており，資源循環による持続可能なシステムの構築が必要になっている．そのために注目されているケミカルリサイクルでは，ポリマーをモノマーに「分解する」という，これまでとは逆の過程の研究が重要になる．

しかし，解重合における反応機構は複雑であり，例えば単純なホモポリマーであるポリスチレン(PSt)でもポリマーからモノマーに至るまでの素反応数は膨大である [1]．そのため，コポリマーやエンジニアリングポリマーのような更に複雑なポリマーの場合，解重合の反応メカニズムをすべて人が考えることは困難になると考えられる．そこで，ポリマーの分解挙動をシミュレートすることによって解重合で起こる反応を網羅し，解重合メカニズムを得ることができるシステムを構築しようと考えた．本報の目的は，どのような手法を用いればポリマーの分解をシミュレートできるかを明らかにすることである．そのために本報では密度汎関数法(DFT)，ニューラルネットワークポテンシャル(NNP)，ReaxFFを用いた分子動力学法(MD)による検討結果を報告する．DFTを用いたMDシミュレーション(DFT-MD)では各ステップにおいてDFT計算によりエネルギーや力を算出するため，精度の高い計算ができる一方，非常に計算コストが高く，大規模な計算が難しいことが知られている．NNPは量子化学計算によるエネルギーや力と原子配置の間の相関を事前学習したポテンシャルであり，精度を損なうことなく量子化学計算の100倍以上の速度で計算できる [2]．NNPを用いたMD(NNP-MD)では各ステップにおいてNNP計算によりエネルギーや力を算出するため，DFT-MDに近い精度で計算できることが期待される．ReaxFFは原子間の距離によって結合次数を決定する分子力場であり，結合の生成や解離を表現することが可能である．このため，ReaxFFを用いたMDで多くの分解シミュレーションが報告されている [3]．本報ではこれら特徴の異なる3つの方法を用いて検証を行った．

解重合の方法として現在主に用いられている熱分解を対象とし [4]，温度や圧力によるモノマー収率の変化が，実験的な傾向と整合するかを評価指標とした．計算対象のポリマーとしては，様々な温度や圧力条件下で実験結果が報告されているPStとした．

2 モデルと計算手法

解重合においては分子内や分子間でのラジカル転位といった，隣り合うモノマー以外での反応が重要であることが分かっているため，ある程度のモデルの大きさが必要である．そのため，本報ではatactic PSt 25量体1本鎖をモデルとした．周期的境界条件下でアモルファス構造を作成し，Hofmannの方法に従って緩和計算を行った [5]．これを20回繰り返し，それぞれを初期構造として反応可能なMD計算を実施し，結果を平均化した．また，温度条件は1500K, 2000K, 3000Kで行い，圧力条件は101 kPa, 1.01 GPaで行った．計算時間については温度条件ごとに異なるが，最大で600 ps行った．いずれもNPTアンサンブルを用いた． DFT-MDはQuantumEspressoで実施し，擬ポテンシャルをUltraSoft，汎関数をPerdew-Burke-Ernzerhof (PBE)とした．NNP-MDでは，NNPとしてMatlantis [6]に実装されているPreFerred Potential (PFP) version v5.0.0(計算モードはCRYSTAL_U0)を用い [2]，MDはAtomic Simulation Environment (ASE)モジュールで実施した．ReaxFFはChenowethらのポテンシャル [7]を用い，MDはLAMMPSで実施した．

3 結果と考察

手法間の精度比較のため，3000Kおよび2000Kで1400fsの計算を行った(Figure 1)．その結果，3000Kではどの手法も短時間で分解が始まった一方，NNP-MDやReaxFFはDFT-MDに比べて分解速度が速くなることが分かった．ReaxFFについてはReaxFF力場が結合解離エネルギーを過小評価する傾向にあるため [8]，速い速度で分解したと考えられる．また，NNPについては高温領域では結合距離が平衡から大きくずれるため，学習が十分でなくなることが原因であると考えられる．一方，2000KではReaxFFの分解速度はDFT-MDに比べてまだ速いが，NNP-MDはほぼ同等になることが分かった．このため，2000K以下の比較的低温領域においては，NNP-MDはDFT-MDに近い精度で計算できると考え，より長時間のMDシミュレーションを実施した．

Figure 1.

 Comparison between reactive MD methods.

温度と圧力違いで，NNP-MDによるモノマー収率がどのように変化するかをFigure 2に示す．なお，Figure 2の3000K, 2000Kについてはn=20のシミュレーションのうち，半数がエラー終了した時点までを示している．3000K, 2000Kともにモノマー収率が途中から減少に転じており，モノマーの再分解が生じていることが分かった．また，1500Kについては101kPaであっても25w%程度までしか分解が進まなかった．これはPSt熱分解の実験結果 [9]と比べても非常に低い．600ps経過後の構造を確認すると，70%の構造はほぼ分解しておらず，30%の構造だけが分解していることが分かった(Figure 3)．このため，分解が進んでいる構造のみの平均値もFigure 2に合わせて示した．その結果，101kPaでは600ps時点で66w%のモノマー収率が得られており，実験結果と整合する結果が得られた．また，圧力が高くなると，モノマー収率はいずれの温度でも大きく低下していることがわかった．この傾向は実験結果 [10]とも整合した結果である．以上のことから，NNP-MDによりPStの熱分解反応のシミュレートが可能になったといえる．

Figure 2.

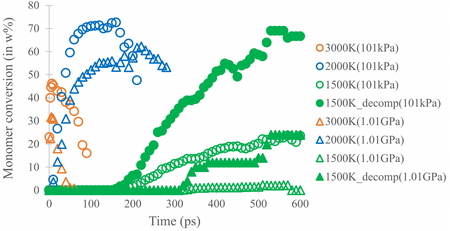
 Results of a long-time simulation using NNP-MD. The filled-in green markers represent averages over the decomposed structures.

Figure 3.

 Examples of structures found after 600 ps under pressure of 101 kPa and temperature of 1500 K. (a) When not decomposed (70% of total), (b) when decomposed (30% of total).

本報では熱分解のシミュレートが可能ということを示したが，1500Kという実験的には非常に高温でのシミュレーションにとどまっていることが課題として残っている．そのため，現在は反応加速方法の検討や，分解を起こしやすい構造の特徴抽出を行っている．更に，ポリスチレン以外のポリマーに対しても用途を広げていくための検討を実施中である．

謝辞

本報のDFT-MD計算は，HPCI システム利用研究課題(課題番号:hp220057)を通じてスーパーコンピュータ「富岳」の計算資源の提供を受け，実施しました．

参考文献

• [1]   J. Huang, X. Cheng, H. Meng, G. Pan, S. Wang, D. Wang, AIP Adv., 10, 085004 (2020). doi:10.1063/5.0013211
• [2]   S. Takamoto, C. Shinagawa, D. Motoki, K. Nakago, W. Li, I. Kurata, et al., Nat. Commun., 13, 2991 (2022). doi:10.1038/s41467-022-30687-9 PMID:35637178
• [3]   S. Q. Nie, M. Q. Chen, Int. J. Hydrogen Energy, 51, 758 (2024). doi:10.1016/j.ijhydene.2023.10.201
• [4]   I. Fukawa, T. Shimoda, ARC Report, RS-1069 (2024).
• [5]   D. Hofmann, L. Fritz, J. Ulbrich, C. Schepers, M. Böhning, Macromol. Theory Simul., 9, 293 (2000).
• [6]   Matlantis (https://matlantis.com/), software as a service style material discovery tool.
• [7]   K. Chenoweth, A. C. T. van Duin, W. A. Goddard, 3rd, J. Phys. Chem. A, 112, 1040 (2008). doi:10.1021/jp709896w PMID:18197648
• [8]   T. Qi, C. W. Bauschlicher, Jr., J. W. Lawson, T. G. Desai, E. J. Reed, J. Phys. Chem. A, 117, 11115 (2013). doi:10.1021/jp4081096 PMID:24094313
• [9]   C. Bouster, P. Vermande, J. Veron, J. Anal. Appl. Pyrolysis, 15, 249 (1989). doi:10.1016/0165-2370(89)85038-7
• [10]   J. Wang, Y. Ma, S. Li, C. Yue, J. Anal. Appl. Pyrolysis, 177, 106366 (2024). doi:10.1016/j.jaap.2024.106366