行列・テンソル分解によるヘテロバイオデータ統合解析の数理

―第5回 ランダムウォーク―

Abstract

生命科学分野で取得されるデータ集合は、雑多（ヘテロ）な構造になり、ヘテロなデータ構造を扱える理論的な枠組みがもとめられている。本連載では、汎用的なヘテロバイオデータの解析手法である行列・テンソル分解を紹介していく。第5回では、第4回で紹介しきれなかったグラフデータの解析の仕方、特にグラフ上でのランダムウォークをベースとした行列・テンソル分解に注目する。

グラフ再訪

これまでの連載［1, 2, 3, 4］のうち第4回［4］では、自己ループの無い無向グラフを扱った。そのようなデータはエッジの有無を意味する対称な正方行列である隣接行列（Adjacency Matrix）として表現され、その後（正規化）グラフラプラシアンという行列に変換し固有値分解（Eigen Value Decomposition；EVD）を行うことで、グラフの最小カット問題が解けることを紹介した。本稿でも引き続き、グラフデータに対するアルゴリズムを紹介する。ただし、第4回［4］のグラフと異なる点としては、第4回［4］では｛0, 1｝のみの値を格納した隣接行列と、0以上の実数の重みを格納した隣接行列とを陽に区別して表記していたが、本稿での議論はどちらに対しても区別なく適用可能であるため、より一般的な重みの隣接行列を想定する。また、ここでは自己ループはあっても良いとする（後述するランダムウォークの計算安定性の観点から自己ループはむしろ推奨）。エッジの向きに関しては、手法ごとに想定するグラフが有向グラフ（非対称な隣接行列）であったり、無向グラフ（対称な隣接行列）であったりするため、必要に応じてその都度明記する。有向グラフにおいては、あるノードから別のノードに張られるエッジの本数を出次数、あるノードが別のノードから張られるエッジの本数を入次数とする。無向グラフにおいては、出次数と入次数の区別が無いため、単に次数とする。また有向グラフを非対称な行列（例：隣接行列A、遷移確率行列P（後述））として表現する際に、ノードjからノードiに張られる有向エッジに関する情報（例：重み、確率（後述））は、A［i,j］やP［i,j］に格納されているものとする。なお、グラフのノード数は全てNとする。

ランダムウォーク

ここでは図1の有向グラフを考える。グラフ上のノードaはノードb, c, dとエッジで接続しており、エッジには各々重み（例：［4, 10, 6］）が付与されているものとする。まずはこの重みベクトルを正規化して確率ベクトルに変換する（例：［4, 10, 6］/20＝［0.2, 0.5, 0.3］）。この正規化を全てのノードに対して同時に行うことは、各ノードの重みベクトルを列ベクトルに持つ非対称隣接行列A（N×N）に対して、ノードの出次数を対角要素に持つ行列D（N×N）の逆行列を、Aの右側からかけることに相当する

  

$$P=A{D}^{-1}$$（1）

（例：$\left[\begin{array}{ccc}4& 5& 2\\ 10& 1& 10\\ 6& 4& 3\end{array}\right]{\left[\begin{array}{ccc}20& & \\ & 10& \\ & & 15\end{array}\right]}^{-1}$）。これにより得られた行列Pを遷移確率行列と呼ぶ。なお、任意のj（1≤j≤N）において${\sum }_i{P}_{ij}=1$である。

図１：ランダムウォークのイメージ

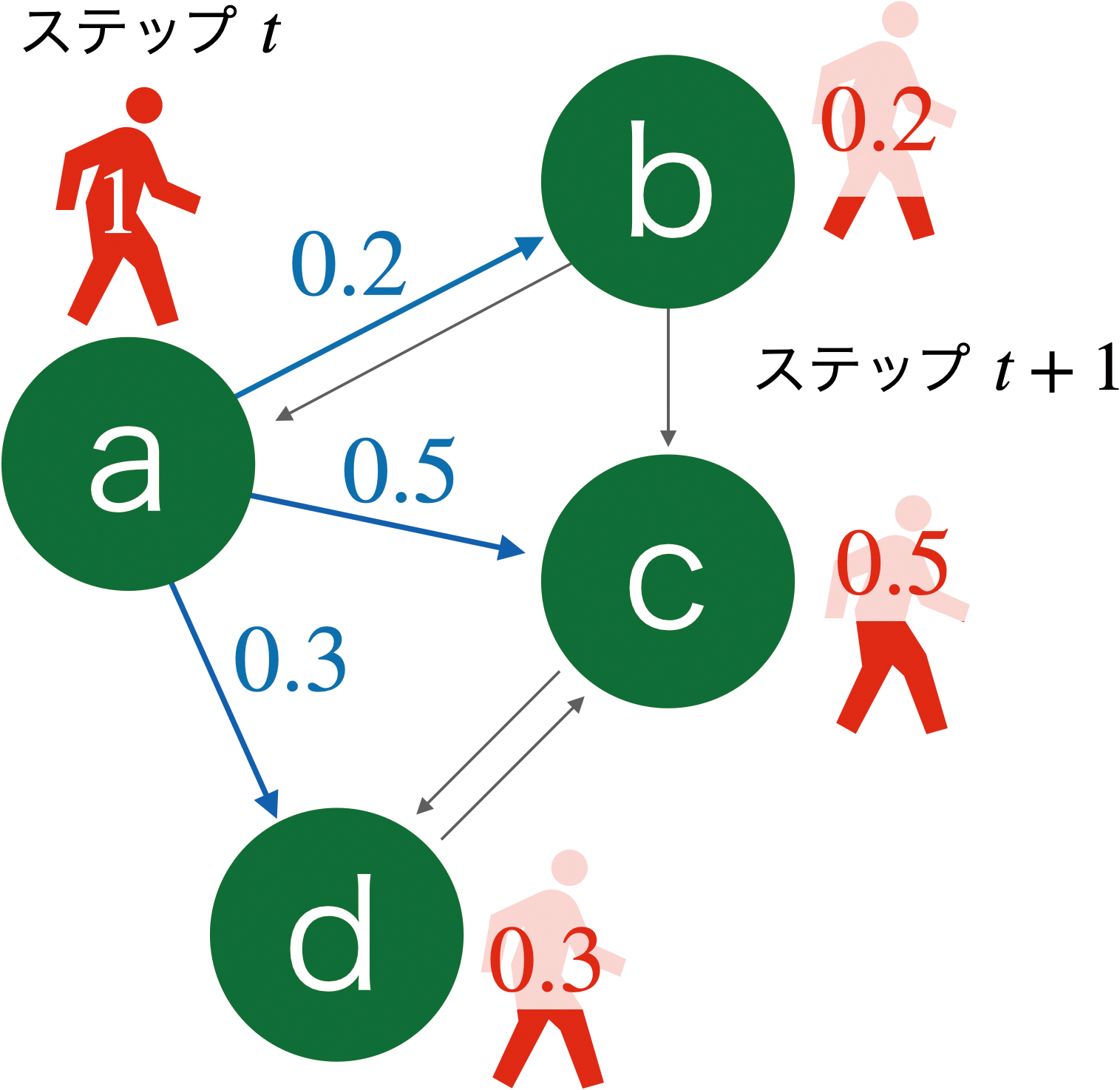
グラフ上のランダムウォーカーは、エッジ上の確率に従い隣接ノードを移動する。移動先ではエッジ上の確率値の分だけそのノードにランダムウォーカーが存在する可能性がある。

今aからb, c, dに確率の値に応じてランダムに移動することを考える。このような操作をランダムウォーク（図1）といい、ランダムウォークを行う仮想的なエージェントをランダムウォーカーという。ここでは「現在の状態は1つ手前の状態にのみ影響を受ける」1次のマルコフ連鎖を仮定している。ある長さNの確率ベクトルx₀を初期値ベクトルとして設定し、これをランダムウォーカーがノードごとに存在する確率とする（図2）。このx₀をPにかけると、全ノードでランダムウォーカーが隣接ノードに一斉に移動することになる。この時に、ノード上のランダムウォーカーの存在確率に、エッジ上の確率がかけられ、次のステップのランダムウォーカーの存在確率x₁が得られる（図2）。

  

$$x_1\leftarrow P{x}_0$$（2）

図２：行列ベクトル積（べき乗法）のイメージ

ステップtにおいてノードごとにランダムウォーカーが存在する確率ベクトルx_tに対して、遷移確率行列Pをかけることで、全ノードでランダムウォーカーを隣接ノードに一斉に移動させ、次のステップt＋1における確率ベクトルx_t+1を求める。べき乗法では、この行列ベクトル積を初期値x₀から定常状態に達するまで繰り返し行い、固有ベクトルx_S（S：逐次計算回数）を求める。

Pが確率性［5］（列ベクトルの和が1であること）、既約性［5］（ランダムウォーカーがどのノードからスタートしても全ノードに行き渡ること）、非周期性［5］（あるノードからスタートしたランダムウォーカーが、元のノードに帰ってくるまでのステップ数に周期がないこと）といった条件を満たす場合は、この操作をt＝1, 2, . . ., S（S：逐次計算回数）と繰り返すことで、段々とベクトルの値が変化しなくなる定常状態（図2）へと達し、特定のベクトルに収束するため、以下の等式が成り立つようになる。

  

$$x_S=P{x}_{S-1}\left(=P^S{x}_0\right)$$（3）

これは、固有ベクトルの定義そのものである（ただし、Pは非対称な正方行列）。読者においては、これまでの連載［1, 2, 3, 4］で紹介してきた「射影」や「パターンの和」に加えて、第3の行列分解のイメージとしてぜひこれを覚えておいて欲しい。すなわち、ここでは固有ベクトルは、十分な時間グラフ上を歩き回ったランダムウォーカーが最終的にどのノードにどの程度とどまるのかを示す「定常状態における存在確率」である。

実際に、上記の計算でEVDをするアルゴリズムがべき乗法（Power method）［5, 6］（図2）であり、初期値ベクトルx₀の値をランダムに変えても、x_Sが固有ベクトルに収束することがわかっている（ただし収束性はPの性質に依存する、cf. Eigen gap［5, 6］）。べき乗法は行列ベクトル積を繰り返すだけでの非常にシンプルなアルゴリズムである（ただし遷移確率行列以外の行列に適用する場合は、オーバーフロー回避のために、ステップtごとにx_tの正規化を伴う［5, 6］）。また行列が十分に疎であった場合、ゼロ要素に関わる計算は省略できることから、疎行列形式との組み合わせにより高速化が望める［7］。べき乗法をベースとしてAugmented implicitly restarted Lanczos bidiagonalization methods（IRLBA）や、Implicitly Restarted Arnoldi Method（IRAM）など、より収束の早いEVDアルゴリズムも提案されており、主成分分析（Principal Component Analysis；PCA）や正準相関分析（Canonical Correlation Analysis；CCA）、対応分析（Correspondence Analysis；CA）など様々な多変量解析手法に利用されている［8, 9］。

Katzの手法［10］はべき乗法と類似した手法であるが、P^tの計算の代わりに、対称な隣接行列の行列積A^tを求める。この時に、グラフ上で移動する距離を制御する非負値のハイパーパラメーターβを利用して、ランダムウォーカーが最初にいたノードから大きく移動し過ぎないようにペナルティを加える。

  

$$\beta A+{\beta }^2{A}^2+\dots =\sum _{t=1}^{\infty }{\beta }^t{A}^t={(I-\beta A)}^{-1}-I$$（4）

なお、ここでは右辺の式変形に行列の幾何級数展開を利用している。他にもハイパーパラメーターでランダムウォークの移動距離をコントロールするアプローチとして、Heat Kernel［11］が挙げられる。

遷移確率行列Pにべき乗法をそのまま適用した場合、ランダムウォーカーが入次数の高いノードにとどまりすぎて、他のノードの確率値がほとんど0になってしまう「シンク」や、ランダムウォーカーが特定の経路だけを循環してしまう「閉路」といった問題があり、グラフ全体の情報を引き出せなかったり、計算の安定性や収束性に影響を及ぼすといったことが知られている［5, 6, 12, 13, 14, 15, 16, 17］。2000年代にGoogleやYahoo!で実際に利用されていた検索アルゴリズムであるPageRank［5, 6, 12, 13, 14, 15, 16, 17］は、こういった問題を解消した手法である。PageRankでは、ランダムウォーカー（PageRankの説明ではネットサーフィンにちなんでランダムサーファーとも呼ばれる）はべき乗法と同様、確率α（0≤α≤1）でエッジ上の遷移確率に従いランダムウォークしつつも、有向グラフ上での接続の有無に関わらず、確率1－αで全てのノードに等確率（1/N）で移動するテレポーテーション（または、ジャンプ、ワープ）と呼ばれる仮定を置くことで、上記の問題を解消している（図3）。

  

$$x_t=\alpha P{x}_{t-1}+(1-\alpha )x_0$$（5）

ただしx₀は全ての要素が1/Nの初期値ベクトルである。αの値は経験的に0.75～0.9程度の値が設定される［5, 6, 12, 13, 16］。なおα＝1の時はPageRankとべき乗法は等価である。

図３：各種ランダムウォーク系手法

PageRank：べき乗法に全ノードに等確率に移動するテレポーテーション項を加えたもの。Personalized PageRank（PPR）：PageRankの初期値ベクトルのうち、特定のノード集合の確率値を大きめに設定したもの。Random Walk with Restart（RWR）：PageRankの初期値ベクトルのうち、特定のノードのみ確率を1にしたもの。ラベル伝播法：グラフ上のランダムウォークで半教師有り学習を行うもの。

なお、上記の非対称隣接行列を転置したA^Tに対して、PageRankを行ったものはCheiRankといい［16］、PageRankの確率値がどれだけ他のノードからランダムウォーカーを集めるのかを意味する権威スコアであるのに対し、CheiRankの確率値はどれだけそのノードが別のノードを参照しているのかを意味するハブスコアとなる。PageRankとは独立に開発されたHITS［5, 10, 13, 16］というアルゴリズムでは、以下のように特異値分解（Singular Value Decomposition；SVD）を非対称隣接行列Aに適用する。

  

$$A=\sigma a{h}^T$$（6）

ただしσはAの最大の特異値、a, hはσに対応する長さNの特異ベクトルである。左特異ベクトルaと右特異ベクトルhが各々権威スコアとハブスコアに相当するため、PageRankとCheiRankの性質を併せ持った手法と言える。HITSの類似手法として、非対称隣接行列から行方向と列方向とで各々正規化した2種類の遷移確率行列を求めてから、それらの行列積のSVDを行うSALSAというアルゴリズムもある［5, 12］。

Personalized PageRank［16］（PPR、またはTopic-specific PageRank、Focused PageRank）と呼ばれるPageRankの拡張手法では、PageRankのテレポーテーション項の初期値ベクトルx₀を等確率とするのではなく、事前にユーザーの興味があるノード集合の確率を大きめに設定しておく（図3）。これにより、有向グラフ上でそれらノードの周辺が重点的にランダムウォークされるようになり、それらの確率値がより大きく算出される。PPRの極端な場合として、グラフ上の1つのノードにだけ1、それ以外は0としたものにRandom Walk with Restart（RWR［16］）がある（図3）。

なお、式（5）のPageRankの逐次式は、定常状態x_t+1＝x_t＝xを仮定することで、逆行列計算により解析的に解くこともできる。

  

$$x=(1-\alpha ){(I-\alpha P)}^{-1}{x}_0$$（7）

ただし、逆行列計算はΟ（N³）だけ計算コストがかかることから、実際には数値計算により逐次的に求めることの方が一般的である。同様の理由で式（4）のKatzの手法も、逆行列計算を回避するために、適当なtの値までで打ち切って計算することが多い。

PageRankはデータの一部にだけラベルが付いている場合に、データ間の類似度から他のラベル未知データにもラベル付けを行う「半教師あり学習」の一種、ラベル伝播法（Label Propagation）［16, 18］と等価である（図3）。ラベル伝播法では、まず第2回［2］で紹介したダミー変数ベクトル（またはOne-hotベクトル）を導入し、あるクラスに属する場合は1、属さないかラベルが未知の場合は0とする長さNのベクトルyを利用して、以下のように逐次的にベクトルf_tを計算する。

  

$$f_t=\alpha E{f}_{t-1}+(1-\alpha )y$$（8）

ただし行列EはE＝D^－1/2 A D^－1/2として、対称な隣接行列Aを次数行列Dで正規化を行ったものである。ここで、両辺に左側からD^1/2をかける。

  

$$D^{1/2}{f}_t=\alpha D^{1/2}S{f}_{t-1}+(1-\alpha )D^{1/2}y$$（9）

そして、式（1）より、EをPに入れ替えると、

  

$$D^{1/2}{f}_t=\alpha P{D}^{1/2}{f}_{t-1}+(1-\alpha )D^{1/2}y$$（10）

となる。最後に$x_t^{\text{'}}=D^{1/2}{f}_t$、$D^{1/2}y=x_0^{\text{'}}$とすることにより、

  

$$x_t^{\text{'}}=\alpha P{x}_{t-1}^{\text{'}}+(1-\alpha )x_0^{\text{'}}$$（11）

となり、実際に式（5）のPageRankの逐次式が得られる。

ランダムウォークのノードのクラスタリング問題への適用も可能である。例えば、Walktrap［19, 20］という手法では、有向グラフ上でのランダムウォークの結果をノード間の距離として、階層的クラスタリングなど各種クラスタリング手法の入力として利用する。マルコフクラスタリング（Markov Clustering［MCL［19, 21］）という手法では、S回逐次計算したべき乗法の結果である

  

$$x_S=P{x}_{S-1}=P^S{x}_0$$（12）

のP^Sの部分を適当な閾値で｛0, 1｝に2値化（枝刈り）し、どのノード同士が同じクラスタに属するのかを示すN×Nのメンバーシップ行列Bを得る。

  

$$B=\mathit{Binarize}(P^S)$$（13）

ただし値により強弱を出すために、何ステップかに1度P^t全体を2乗した後に正規化する操作が入る。Leading Eigenvector［19, 22］は、対称な隣接行列A、次数ベクトルd、リンクの本数$L=\sum A/2$とした時に、以下のモジュラリティ行列Q

  

$$Q=A-\frac{1}{2L}{dd}^T$$（14）

に対してEVDを適用する手法であり、第4回［4］で紹介したラプラシアン固有マップ（Laplacian Eigenmaps；LEM）と同様、クラス数－1だけ固有ベクトルを計算した後に、k-meansなど別のクラスタリング手法を適用することで2値化する。期待値から逸脱した残差に対して行列分解するこの目的関数は、第4回［4］で紹介したCAの目的関数（Pearson残差）とも類似している。なお、この目的関数を近似的に最適化する別のクラスタリング手法としてLouvain法［23, 24, 25, 26］があり、非常に高速であり、かつUMAPの散布図上のクラスタ構造とよく一致したクラスタリング結果が得られることから、1細胞オミックス分野で現在デファクトスタンダード的手法となっている。

生命科学分野で得られるデータ解析では「一部のよく知られたデータを除き、ほとんどのデータに属性情報が与えられていない（例：機能未知、未アノテーション）」という状況がしばしば起きる。このようなデータの解析においては、Guilt-By-Association（GBA）という原理が適用される（図4）。GBAとは、グラフ上で属性未知のノードaと属性既知のノードbが関連づけられた場合、bの属性をaの属性としても流用するという考え方である（例：疾患X関連遺伝子bと共発現していた遺伝子aもまた疾患Xに関係するだろう）。

図４：Guilt-By-Association（GBA）の原理

元々は「関連する人々が有罪であるための個々への罪の帰属（証明のない）」を意味する法律用語。転じて、生命科学分野においては「ある生体分子や現象間の何らかの関連性を根拠に、片方の属性情報をもう片方に流用する」というアプローチを指す。

GBAの原理に基づき、少しでも参考になりそうな付加情報を取り込んで、未知のデータ間のリンク（Missing link）を予測するという方針が取られるが、ランダムウォーク系の手法はまさにこのような解析において基盤技術となっている。例えば、遺伝子-疾患の関連性の優先順位づけ（Gene Prioritization）［27, 28, 29, 30, 31, 32, 33］、ドラッグリポジショニング［34, 35, 36, 37］、タンパク質間相互作用（Protein-Protein Interaction；PPI）［38, 39］、micro RNA、lnc RNA、circ RNAなどのnon-coding RNAの機能予測や疾患との関連性予測［40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50］、マイクロバイオームと疾患との関連性予測［51, 52, 53, 54］、メタボロームデータのアノテーション［55, 56］、遺伝子制御ネットワーク（Gene Regulatory Network；GRN）［57, 58, 59, 60, 61, 62］、ゲノムワイド関連解析（Genome-wide Association Study；GWAS）［63］、タンパク質折りたたみ［64］、マルチオミックス解析［65］など、数多くの問題設定においてランダムウォーク系の手法が活用されている。昨今では、データがノイジーなシングルセルオミックスデータ（例：scRNA-Seq、scATAC-Seq、scHi-Cなど）における欠損値補完（Imputation）［66, 67, 68, 69, 70, 71, 72, 73, 74］や、計測値の平滑化（Smoothing）［75, 76］、細胞ダウンサンプリング［77］、細胞間相互作用［78, 79］といった解析にも活用されつつある。

ランダムウォークの拡張

関連するデータは少しでも取り込んで、データ解析の性能を向上させようという動きは生命科学分野以外にも見られる。特にWebデータマイニングの分野においては、Heterogenous Information Network（HIN）というキーワードの下、精力的にそのような研究が取り組まれている［80, 81, 82］。HINが扱う課題は、関連データを統合しつつも、データの種類が異なる場合には、ノードの次数分布やノード間の距離といった統計的性質や、データの品質も異なることから、これらの違いを補正しつつ1つのモデルとしてどのように扱うかという点にある。

例えばA（例：遺伝子）とB（例：疾患）の関係性を調べる解析を考えてみる（図5）。既知の両者の関係性（例：OMIM, DisGeNET）をA-B隣接行列として表現すると、全組み合わせに対してごく一部しか関係性が知られていないためかなり疎な行列になるが、これに加えてA-A隣接行列（例：PPI, GRN）や、B-B隣接行列（例：Disease Ontology）を統合し、1つのグラフとした上でランダムウォークし、未知の遺伝子と疾患間のMissing linkを推定するということがよく行われる［80, 81, 82］。この時にHIN的なモデルでは、遺伝子や疾患といったデータの種類の違いを考慮し、A→A、A⇄B、B→A間の移動に関する遷移確率に関して別々にランダムウォークをしたり、同種ネットワーク間と異種ネットワーク間のランダムウォークで、移行のしやすさを変えるといった工夫がなされる。このようなランダムウォークモデルは、Multiplex Random Walk［83, 84］、Multi-layer Random Walk［85, 86］、Colored Random Walk［87］など様々な呼び方がされている。

図５：Heterogenous Information Network（HIN）の技術

左上：A-A隣接行列（例：遺伝子間制御ネットワーク）、A-B隣接行列（例：疾患関連遺伝子データベース）、B-B隣接行列（例：疾患間類似度）を1つの行列としてマージした行列。データ構造としては1つの行列になっているが、これらは統計学的性質やデータの品質が異なることから、データの出所を考慮したモデリングが必要となる。右上：Meta-pathでは、始点（例：A）や終点（例：D）、パス長（例：2）などを事前に設定し、取りうるパスを列挙した上で、パスごとに解析手法を適用する。下：符号付き有向グラフに対するランダムウォークでは、ランダムウォーカーの符号にエッジの符号がかかった値が隣接ノードにおける符号となる。この性質を利用して、味方の味方（＝味方）、味方の敵（＝敵）、敵の味方（＝敵）、敵の敵（＝味方）を区別できる。

HIN分野の代表的なアプローチであるMeta-path［80, 81, 82］では、例えばA（例：遺伝子）からD（例：疾患）の関係性を知りたいとなった場合に、他にも関連するBやCといった情報を経由する経路（パス）も考慮し、A→D、A→B→D、A→C→B→Dのように、明示的にランダムウォークで通るパスを区別しておき、パスごとに別々にモデルを適用して最後に解析結果を（重み付きで）マージしたり、性能の良いパスだけを採用するといった方針がとられる（図5）。

類似した考え方である符号付きランダムウォークでは、エッジに付随した重みに正の値、負の値が両方含まれているタイプの非対称隣接行列（符号付き有向グラフ）を、正の隣接行列、負の隣接行列に分離して、別々にランダムウォークを行う（図5）。ランダムウォーカーの符号にエッジの符号がかかった値が隣接ノードにおける符号となる性質を利用して、味方の味方（＝味方）、味方の敵（＝敵）、敵の味方（＝敵）、敵の敵（＝味方）を区別できる。これにより、初期ランダムウォーカーから見た味方度合い、敵度合いを全ノードに対してスコア化できる。既に符号を考慮したPageRank［88］、HITS［88］、PPR［89］、RWR［89］、スペクトラルクラスタリング［90］、Leading Eigenvector［90］、ラベル伝播法［91］など、様々な手法が提案されている。

生命科学分野においては、上記のようなランダムウォークの拡張手法は、疾患関連遺伝子予測［92］やドラッグリポジショニング［93, 94, 95, 96, 97, 98］、non-coding RNAの機能予測や疾患との関連性予測［99, 100, 101, 102, 103, 104, 105, 106］、発現変動遺伝子やコピー数多型の検出［107］、マイクロバイオームと薬剤との関連性予測［108］、漢方データのアノテーション［109］、といった様々な問題に適用されている。

データの種類の違いを考慮したランダムウォークをする別の方法としては、テンソルデータにランダムウォーク系手法を適用するアプローチが挙げられる。まずN×Nの非対称隣接行列がMセットある場合、それらを奥行き方向で束ねることでN×N×Mの3階テンソル$𝒜$（図6）になるが、これに対して

  

$$\begin{array}{c}{x}_t=𝒜{\times }_2{y}_{t-1}{\times }_3{z}_{t-1}\\ y_t=𝒜{\times }_1{x}_t{\times }_3{z}_{t-1}\\ z_t=𝒜{\times }_1{x}_t{\times }_2{y}_t\end{array}$$（15）

という高次のべき乗法を適用するHITSのテンソル拡張であるTOPHITS［110, 111］が挙げられる。ただし、×_mはテンソルのm番目のモードに作用するモード積である（第3回［3］）。原著論文［110, 111］では、PageRankが想定するようなWebサイト間のハイパーリンクの隣接行列が話題ごとにあるテンソルデータであることから、x, y, zをそれぞれ、ハブスコア、権威スコア、トピックスコアとしている。同様に、N×Nの遷移確率行列がMセットある場合、N×N×Mの3階テンソル$𝒫$（図6）になり、これに対してテンソル分解を適用した事例もある［112］。

図６：ランダムウォークとテンソル

TOPHITSでは複数の隣接行列に高次べき乗法を適用する。正規化後の複数の遷移確率行列に対してテンソル分解を行った事例もある。第4回［4］で紹介したハイパーグラフ上のランダムウォーク系手法としてHypergraph PageRankや、Hypergraph RWR、Hypergraphラベル伝播法などがある。m次マルコフ連鎖は、m＋1階テンソルに相当し、このデータに対するランダムウォーク手法としてZ-固有ベクトルやMultilinear PageRankなどがある。

第4回［4］で紹介したグラフを拡張した概念であるハイパーグラフは、多対多の関係性をハイパーエッジとして集合的にとらえることができる（図6）。N×Nのハイパーグラフ上の遷移確率行列$\mathrm{\mathscr{H}}$は、接続行列H（N×E、Eはハイパーエッジ数）、重み行列W（E×E）、ハイパーエッジ次数行列D_e（E×E）、ノード次数行列（N×N）として以下のように求められる。

  

$$\mathrm{\mathscr{H}}=\mathit{HW}{D}_e^{-1}{H}^T{D}_v^{-1}$$（16）

なお、任意のj（1≤j≤N）において${\sum }_i{\mathrm{\mathscr{H}}}_{\mathit{ij}}=1$である。この行列に対するランダムウォーク手法としてHypergraph PageRank［113］、Hypergraph RWR［114, 115, 116, 117］、Hypergraph Label Propagation［118］などがある。

グラフ上で2ステップ以上離れたノードまでの依存関係を考慮する、2次以上の高次マルコフ連鎖を考えたランダムウォークでは、m次マルコフ連鎖に対して、m＋1階遷移確率テンソル$𝒵$が設定される。例えば2次マルコフ連鎖を仮定して、ステップtがそれより手前の2ステップt－1とt－2にのみ依存するとした場合、$𝒵$は3階テンソルとなる（図6）。ただし任意のi（1≤i≤N）において${\sum }_{\mathit{jk}}{𝒵}_{\mathit{ijk}}=1$である。この高階テンソルに対して、

  

$$x_t\leftarrow 𝒵{\times }_2{x}_{t-1}{\times }_3{x}_{t-1}$$（17）

（またはx＝$𝒵$x²と表記する）のようにランダムウォークする手法として、Z-固有ベクトル［111, 119, 120, 121, 122, 123］）や、Multilinear PageRank［124］がある。このようなテンソル版ランダムウォーク手法は、がん関連遺伝子の予測［114］、ドラッグリポジショニング［115］、Non-coding RNAの機能予測［116］、マイクロバイオーム［117］などに利用されている。またZ-固有ベクトルは、集団遺伝学におけるHardy-Weinberg平衡（集団内の遺伝的な平衡状態を示す原理）と等価であることがわかっている［121, 122］。

ランダムウォークと系列データ

遷移確率行列の確率値に基づき、実際に系列データを生成できる。これにより、グラフデータの系列データ向けモデルへの流用も可能である（図7）。例えばグラフ分散表現学習、またはグラフ埋め込み（Embedding）と呼ばれる分野では、グラフを系列データ化した後に、次元圧縮を適用することで、グラフという特殊なデータ構造をより扱いやすい数値ベクトルに変換し、その後に次元圧縮、クラスタリング、回帰、判別などより一般的な機械学習のタスクに利用する。例えば、系列化したデータに対してニューラルネットワークを利用した次元圧縮手法word2vecを適用する手法としてDeepWalkやnode2vecが挙げられ［125, 126］、第4回［4］で紹介したLEMもグラフ埋め込み手法の一種とも言える（余談だが、分散表現学習分野では、ベクトル化するという意味で～2vecという手法名が付けられることが多い）。このようなアプローチは、生命科学分野においては、ドラッグリポジショニング［127, 128］や、non-coding RNAの機能予測［129, 130］、時系列scRNA-Seqデータの統合「131」、生命医科学分野で利用されるグラフ状の知識データベース（Resource Description Framework；RDF）の次元圧縮［132］といった研究に利用されている。またHIN特化型のグラフ埋め込みであるmetapath2vecやHIN2Vecといった手法も提案されている［133］。

図７：ランダムウォークと系列データ

遷移確率行列から系列データを生成し、様々な系列データ向け解析手法を適用することが可能である。また逆に、系列データから遷移確率行列を学習（行列化）し、ランダムウォーク系解析手法を適用することも可能である。

また逆に系列データから遷移確率行列を学習（行列化）し、ランダムウォーク系の手法を適用することも可能である（図7）。例えば、Goncalvesらの研究［134］では、時系列計測したDNAマイクロアレイデータに対しHeat Kernelを利用したランダムウォークを適用することにより、酵母の熱ストレスに関連した転写因子の優先順位付けを行なっている。

最後に1つ面白い事実を紹介しておく。上述したグラフ埋め込み手法は、どれも行列分解として定式化できることが近年示されている［135］（ただし、現段階では数式上だけの話しであり、具体的にどのように最適化することで、そのような行列分解を直接計算できるようになるのかは不明である）。一見行列分解とは関係の無い手法が、行列分解として後から再定式化されるケースはこれまでに幾つもあり（トピックモデル［136］、k-means［137］、スペクトラルクラスタリング［138］、DBSCAN［138］、隠れマルコフモデル［139］、ニューラルネットワーク［140, 141］）、機械学習分野における1つの潮流となっている。

おわりに

今回は、第4回［4］で紹介しきれなかったグラフデータ解析、特にグラフ上でのランダムウォークをベースとした行列・テンソル分解手法を紹介した。このようなアプローチは、GBA原理に基づき、関連するデータを少しでも寄せ集めることで、アノテーションが不十分なデータの意味づけや、ノイジーなデータの欠損値補完などに利用されている。特に昨今HINをキーワードに進められている、データの種類の違いを考慮したグラフ上でのランダムウォークは、生命科学の問題設定に深く通じるものであり、またテンソル分解との親和性が高く、今後様々な手法が提案されていくと思われる。また、遷移確率行列（グラフ）と系列データとは互いに変換可能であり、それに各分野で提案されたモデルを異なる分野に流用可能であることが面白い。次回は、系列データにより特化した行列・テンソル分解について紹介する。

References

• [1]  Tsuyuzaki, K. (2021/4/23). Mathematics for Heterogeneous Biological Data Fusion Analysis with Matrix-Tensor Factorization―Part I. Matrix Factorization―. JSBi Bioinformatics Review, 1(2), 18-25. 10.11234/jsbibr.2021.1
• [2]  Tsuyuzaki, K. (2021/10/5). Mathematics for Heterogeneous Biological Data Fusion Analysis with Matrix-Tensor Factorization―Part II. Simultaneous Matrix Factorization―. JSBi Bioinformatics Review, 2(1), 15-29. 10.11234/jsbibr.2021.6
• [3]  Tsuyuzaki, K. (2022/6/2). Mathematics for Heterogeneous Biological Data Fusion Analysis with Matrix-Tensor Factorization―Part III. Tensor Factorization―. JSBi Bioinformatics Review, 3(1), 20-33. 10.11234/jsbibr.2022.1
• [4]  Tsuyuzaki, K. (2022/11/1). Mathematics for Heterogeneous Biological Data Fusion Analysis with Matrix-Tensor Factorization―Part IV. Categorical Data, Distance, and Graph―. JSBi Bioinformatics Review, 3(2), 33-46. 10.11234/jsbibr.2022.2
• [5]  Amy N. Langville. & Carl D. Meyer. & 岩野和生. & 黒川利明. & 黒川洋. （2009/10/10）．PageRankの数理．共立出版
• [6]  神谷紀生 & 北栄輔．（1999/2/25）．計算による線形代数（工学数学講座2）．共立出版
• [7]  Tsuyuzaki, K. & Sato, H. & Sato, K. & Nikaido, I. (2020). Benchmarking principal component analysis for large-scale single-cell RNA-sequencing. Genome Biology, 21(1):9, 10.1186/s13059-019-1900-3
• [8]  Bie, T.D. & Cristianini, N. & Rosipal, R. (2005). Eigenproblems in Pattern Recognition. Handbook of Geometric Computing. Springer, 10.1007/3-540-28247-5_5
• [9]  Hsu, L.L. & Culhane, A.C. (2023). Correspondence analysis for dimension reduction, batch integration, and visualization of single-cell RNA-seq data. Scientific Report, 13(1197), 10.1038/s41598-022-26434-1
• [10]  Singh-Blom, U.M. & Natarajan, N. & Tewari, A. & Woods, J.O. & Dhillon, I.S. & Marcotte, E.M. (2013). Prediction and validation of gene-disease associations using methods inspired by social network analyses. PLoS One, 8(5), e58977. 10.1371/annotation/5aeb88a0-1630-4a07-bb49-32cb5d617af1
• [11]  Chen, Y. & Wang, W. & Zhou, Y. & Shields, R. & Chanda, S.K. & Elston, R.C. & Li, J. (2011). In silico gene prioritization by integrating multiple data sources. PLoS One. 6(6), e21137. 10.1371/journal.pone.0021137
• [12]  梅澤克之. & Neil Rubens. & 松田健. & 三川健太. & 水野信也. & 山本健司．（2020/10/30）．情報検索エンジンの実装と評価．森北出版
• [13]  Christopher D. Manning. & Prabhakar Raghavan. & Hinrich Schutze. & 岩野和生. & 黒川利明. & 濱田誠司. & 村上明子．（2012/6/23）．情報検索の基礎．共立出版
• [14]  Amy N. Langville. & Carl D. Meyer. & 岩野和生. & 中村英史. & 清水咲里．（2015/7/23）．レイティング・ランキングの数理．共立出版
• [15]  ジョンマコーミック. & 長尾高弘．（2012/7/19）．世界で最も強力な9のアルゴリズム．日経BP社
• [16]  ダヌシカ・ボレガラ. & 岡崎直観. & 前原貴憲．（2016/8/25）．ウェブデータの機械学習（機械学習プロフェッショナルシリーズ）．講談社
• [17]  Gleich, D.F. (2015). Pagerank beyond the Web. SIAM Review, 57(3), 321-363.
• [18]  Chiyomaru, K. & Takemoto, K. (2021/4/23). Network propagation for biological network analysis―. JSBi Bioinformatics Review, 1(2), 26-36. 10.11234/jsbibr.2021.2
• [19]  Santo Fortunato, (2010). Community detection in graphs, Physics Reports, 486 (3-5), 75-174. 10.1016/j.physrep.2009.11.002
• [20]  Pons, P. & Latapy, M. (2005). Computing Communities in Large Networks Using Random Walks, Computer and Information Sciences - ISCIS 2005. ISCIS 2005. Lecture Notes in Computer Science, 3733. 10.1007/11569596_31
• [21]  Dongen, V. (2000). Graph clustering by flow simulation. Ph.D. thesis, University of Utrecht.
• [22]  Newman, M.E. (2006). Finding community structure in networks using the eigenvectors of matrices. Physical review E: Statistical, nonlinear, and soft matter physics. 74(3 Pt 2), 036104. 10.1103/PhysRevE.74.036104
• [23]  Blondel, V.D. & Guillaume, J.-L. & Lambiotte, R. & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment.
• [24]  Nakajima, N. (2022/11/1). Trends and outlook of single-cell analysis. JSBi Bioinformatics Review, 3(2), 61-74. 10.11234/jsbibr.2022.4
• [25]  F.メンツァー. & S.フォルトゥナート. & C.A.デービス. & 笹原和俊（2024/1/4）．ネットワーク科学入門：Pythonで学ぶデータ分析とモデリング．丸善出版
• [26]  Albert-László Barabási. & 池田裕一. & 井上寛康. & 谷澤俊弘. & 京都大学ネッワーク社会研究会．（2019/2/27）．ネットワーク科学：ひと・もの・ことの関係性をデータから解き明かす新しいアプローチ．共立出版
• [27]  Luo, J. & Liang, S. (2015). Prioritization of potential candidate disease genes by topological similarity of protein-protein interaction network and phenotype data. Journal of Biomedical Informatics. 53, 229-36. 10.1016/j.jbi.2014.11.004
• [28]  Jiang, R. (2015). Walking on multiple disease-gene networks to prioritize candidate genes. Journal of Molecular Cell Biology. 7(3), 214-30. 10.1093/jmcb/mjv008
• [29]  Köhler, S. & Bauer. S. & Horn. D. & Robinson, P.N. (2008). Walking the interactome for prioritization of candidate disease genes. The American Journal of Human Genetics, 82(4), 949-58. 10.1016/j.ajhg.2008.02.013
• [30]  Vanunu, O. & Magger, O. & Ruppin, E. & Shlomi, T. & Sharan, R. (2010). Associating genes and protein complexes with disease via network propagation. PLoS Computational Biology, 6(1), e1000641. 10.1371/journal.pcbi.1000641
• [31]  Li, Y. & Patra, J.C. (2010). Genome-wide inferring gene-phenotype relationship by walking on the heterogeneous network. Bioinformatics, 26(9), 1219-24. 10.1093/bioinformatics/btq108
• [32]  Valentini, G. & Armano, G. & Frasca, M. & Lin, J. & Mesiti, M. & Re, M. (2016). RANKS: a flexible tool for node label ranking and classification in biological networks. Bioinformatics, 32(18), 2872-2874. 10.1093/bioinformatics/btw235
• [33]  Zhang, Y. & Liu. J. & Liu, X. & Fan, X. & Hong, Y. & Wang, Y. & Huang, Y. & Xie, M. (2018). Prioritizing disease genes with an improved dual label propagation framework. BMC Bioinformatics, 19(1), 47. 10.1186/s12859-018-2040-6
• [34]  Lu, Y. & Guo, Y. & Korhonen, A. (2017). Link prediction in drug-target interactions network using similarity indices. BMC Bioinformatics, 18(1), 39. 10.1186/s12859-017-1460-z
• [35]  Seal, A. & Ahn, Y.Y. & Wild, D.J. (2015). Optimizing drug-target interaction prediction based on random walk on heterogeneous networks. Journal of Cheminformatics. 7, 40. 10.1186/s13321-015-0089-z
• [36]  Liu, H. & Song, Y. & Guan, J. & Luo, L. & Zhuang, Z. (2016). Inferring new indications for approved drugs via random walk on drug-disease heterogenous networks. BMC Bioinformatics. 17(Suppl 17), 539. 10.1186/s12859-016-1336-7
• [37]  Wang, W. & Yang, S. & Zhang, X. & Li, J. (2014). Drug repositioning by integrating target information through a heterogeneous network model. Bioinformatics. 30(20), 2923-2930. 10.1093/bioinformatics/btu403
• [38]  Barel, G. & Herwig, R. (2020). NetCore: a network propagation approach using node coreness. Nucleic Acids Research. 48(17), e98. 10.1093/nar/gkaa639
• [39]  Lu, S. & Yan, Y. & Li, Z. & Chen, L. & Yang, J. & Zhang, Y. & Wang, S. & Liu, L. (2017). Determination of Genes Related to Uveitis by Utilization of the Random Walk with Restart Algorithm on a Protein-Protein Interaction Network. International Journal of Molecular Sciences. 18(5), 1045. 10.3390/ijms18051045
• [40]  Chen, X. (2015). KATZLDA: KATZ measure for the lncRNA-disease association prediction. Scientific Reports, 5, 16840. 10.1038/srep16840
• [41]  Zhang, Y. & Chen, M. & Huang, L. & Xie, X. & Li, X. & Jin, H. & Wang, X. & Wei, H. (2021). Fusion of KATZ measure and space projection to fast probe potential lncRNA-disease associations in bipartite graphs. PLoS One. 16(11), e0260329. 10.1371/journal.pone.0260329
• [42]  Chen, M. & Deng, Y. & Li, Z. & Ye, Y. & He, Z. (2023). KATZNCP: a miRNA-disease association prediction model integrating KATZ algorithm and network consistency projection. BMC Bioinformatics, 24(1), 229. 10.1186/s12859-023-05365-2
• [43]  Vural, H. & Kaya, M. (2018). Prediction of new potential associations between LncRNAs and environmental factors based on KATZ measure. Computers in Biology and Medicine. 102, 120-125. 10.1016/j.compbiomed.2018.09.019
• [44]  Lei, X. & Bian, C. (2020). Integrating random walk with restart and k-Nearest Neighbor to identify novel circRNA-disease association. Scientific Reports, 10(1), 1943. 10.1038/s41598-020-59040-0
• [45]  Vural, H. & Kaya, M. & Alhajj, R. (2019). A Model Based on Random Walk with Restart to Predict CircRNA - Disease Associations on Heterogeneous Network, 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), 929-932. 10.1145/3341161.3343514
• [46]  Zou, Q. & Li, J. & Song, L. & Zeng, X. & Wang, G. (2016). Similarity computation strategies in the microRNA-disease network: a survey. Briefings in Functional Genomics, 15(1), 55-64. 10.1093/bfgp/elv024
• [47]  Qu, J. & Wang, C.C. & Cai, S.B. & Zhao, W.D. & Cheng, X.L. & Ming, Z. (2021). Biased Random Walk With Restart on Multilayer Heterogeneous Networks for MiRNA-Disease Association Prediction. Frontiers in Genetics. 12, 720327. 10.3389/fgene.2021.720327
• [48]  Chen, X. & You, Z.H. & Yan, G.Y. & Gong, D.W. (2016). IRWRLDA: improved random walk with restart for lncRNA-disease association prediction. Oncotarget, 7(36), 57919-57931. 10.18632/oncotarget.11141
• [49]  Gu. C. & Liao, B. & Li, X. & Cai, L. & Li, Z. & Li, K. & Yang, J. (2017). Global network random walk for predicting potential human lncRNA-disease associations. Scientific Reports, 7(1), 12442. 10.1038/s41598-017-12763-z
• [50]  Xiao, Y. & Xiao, Z. & Feng, X. & Chen, Z. & Kuang, L. & Wang, L. (2020). A novel computational model for predicting potential LncRNA-disease associations based on both direct and indirect features of LncRNA-disease pairs. BMC Bioinformatics, 21(1), 555. 10.1186/s12859-020-03906-7
• [51]  Chen, X. & Huang, Y.A. & You, Z.H. & Yan, G.Y. & Wang, X.S. (2017). A novel approach based on KATZ measure to predict associations of human microbiota with non-infectious diseases. Bioinformatics. 33(5), 733-739. 10.1093/bioinformatics/btw715
• [52]  Zhu, L. & Duan, G. & Yan, C. & Wang, J. (2019). Prediction of Microbe-Drug Associations Based on KATZ Measure, 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), 183-187. 10.1109/BIBM47256.2019
• [53]  Li, S. & Xie, M. & Liu, X. (2019). A Novel Approach Based on Bipartite Network Recommendation and KATZ Model to Predict Potential Micro-Disease Associations. Frontiers in Genetics, 10, 1147. 10.3389/fgene.2019.01147
• [54]  Zou, S. & Zhang, J. & Zhang, Z. (2017). A novel approach for predicting microbe-disease associations by bi-random walk on the heterogeneous network. PLoS One, 12(9), e0184394. 10.1371/journal.pone.0184394
• [55]  Lei, X. & Zhang, C. (2019). Predicting metabolite-disease associations based on KATZ model. BioData Mining, 12, 19. 10.1186/s13040-019-0206-z
• [56]  Hu, Y. & Zhao, T. & Zhang, N. & Zang, T. & Zhang, J. & Cheng, L. (2019). Identifying diseases-related metabolites using random walk. BMC Bioinformatics, 19(Suppl 5), 116. 10.1186/s12859-018-2098-1
• [57]  González-Gomariz, J. & Serrano, G. &, Tilve-Álvarez, C.M. & Corrales, F.J. & Guruceaga, E. & Segura, V. (2020). UPEFinder: A Bioinformatic Tool for the Study of Uncharacterized Proteins Based on Gene Expression Correlation and the PageRank Algorithm. Journal of Proteome Research, 19(12), 4795-4807. 10.1021/acs.jproteome.0c00364
• [58]  Zhong, J. & Han, C. & Wang, Y. & Chen, P. & Liu R. (2022). Identifying the critical state of complex biological systems by the directed-network rank score method. Bioinformatics, 38(24), 5398-5405. 10.1093/bioinformatics/btac707
• [59]  Zhou, S. & Huang, Y.E. & Liu, H. & Zhou, X. & Yuan, M. & Hou, F. & Wang, L. & Jiang, W. (2021). Single-cell RNA-seq dissects the intratumoral heterogeneity of triple-negative breast cancer based on gene regulatory networks. Nucleic Acids - Molecular Therapy, 23, 682-690. 10.1016/j.omtn.2020.12.018
• [60]  Zhang, K. & Wang, M. & Zhao, Y. & Wang, W. (2019). Taiji: System-level identification of key transcription factors reveals transcriptional waves in mouse embryonic development. Science Advances, 5(3), eaav3262. 10.1126/sciadv.aav3262
• [61]  Liu, W. & Sun, X. & Peng, L. & Zhou, L. & Lin, H. & Jiang, Y. (2020). RWRNET: A Gene Regulatory Network Inference Algorithm Using Random Walk With Restart. Frontiers in Genetics, 11, 591461. 10.3389/fgene.2020.591461
• [62]  Erten, C. & Houdjedj, A. & Kazan, H. (2021). Ranking cancer drivers via betweenness-based outlier detection and random walks. BMC Bioinformatics, 22(1), 62. 10.1186/s12859-021-03989-w
• [63]  Barrio-Hernandez, I. & Schwartzentruber, J. & Shrivastava, A. & Del-Toro, N. & Gonzalez, A. & Zhang, Q. & Mountjoy, E. & Suveges, D. & Ochoa, D. & Ghoussaini, M. & Bradley, G. & Hermjakob, H. & Orchard, S. & Dunham, I. & Anderson, C.A. & Porras, P. & Beltrao, P. (2023). Network expansion of genetic associations defines a pleiotropy map of human cell biology. Nature Genetics, 55(3), 389-398. 10.1038/s41588-023-01327-9
• [64]  Shao, J. & Liu, B. (2021). ProtFold-DFG: protein fold recognition by combining Directed Fusion Graph and PageRank algorithm. Briefings in Bioinformatics, 22(3), bbaa192. 10.1093/bib/bbaa192
• [65]  Gentili, M. & Martini, L. & Sponziello, M. & Becchetti, L. (2022). Biological Random Walks: multi-omics integration for disease gene prioritization. Bioinformatics, 38(17), 4145-4152. 10.1093/bioinformatics/btac446
• [66]  Yu, J. & Sun, D. & Hou, Z. & Wu, L.-Y. (2022). Single-Cell ATAC-seq analysis via Network Refinement with peaks location information, bioRxiv, 10.1101/2022.11.18.517159
• [67]  Jeong, H. Liu, Z. (2020). PRIME: a probabilistic imputation method to reduce dropout effects in single-cell RNA sequencing. Bioinformatics, 36(13), 4021-4029. 10.1093/bioinformatics/btaa278
• [68]  Trimbour, R. & Deutschmann, I.M. & Cantini, L. (2023). Molecular mechanisms reconstruction from single-cell multi-omics data with HuMMuS, bioRxiv, 10.1101/2023.06.09.543828
• [69]  Zhou, J. & Ma, J. & Chen, Y. & Cheng, C. & Bao, B. & Peng, J. & Sejnowski, T.J. & Dixon, J.R. & Ecker, J.R. (2019). Robust single-cell Hi-C clustering by convolution- and random-walk-based imputation. PNAS, 116(28), 14011-14018. 10.1073/pnas.1901423116
• [70]  Yu, M. & Abnousi, A. & Zhang, Y. & Li, G. & Lee, L. & Chen, Z. & Fang, R. & Lagler, T.M. & Yang, Y. & Wen, J. & Sun, Q. & Li, Y. & Ren, B. & Hu, M. (2021). SnapHiC: a computational pipeline to identify chromatin loops from single-cell Hi-C data. Natrue Methods, 18(9), 1056-1059. 10.1038/s41592-021-01231-2
• [71]  Zhang, R. & Zhou, T. & Ma, J. (2022). Ultrafast and interpretable single-cell 3D genome analysis with Fast-Higashi. Cell Systems, 13(10), 798-807.e6. 10.1016/j.cels.2022.09.004
• [72]  van Dijk, D. & Sharma, R. & Nainys, J. & Yim, K. & Kathail, P. & Carr, A.J. & Burdziak, C. & Moon, K.R. & Chaffer, C.L. & Pattabiraman, D. & Bierie, B. & Mazutis, L. & Wolf, G. & Krishnaswamy, S. & Pe’er, D. (2018). Recovering Gene Interactions from Single-Cell Data Using Data Diffusion. Cell. 174(3), 716-729.e27. 10.1016/j.cell.2018.05.061
• [73]  Li, X. & Lee, L. & Abnousi, A. & Yu, M. & Liu, W. & Huang, L. & Li, Y. & Hu, M. (2022). SnapHiC2: A computationally efficient loop caller for single cell Hi-C data. Comput Struct Biotechnol J. 20, 2778-2783. 10.1016/j.csbj.2022.05.046.
• [74]  Liu, W. & Zhong, W. & Giusti-Rodríguez, P. & Wang, G.W. & Hu, M. & Li, Y. (2023). SnapHiC-G: identifying long-range enhancer-promoter interactions from single-cell Hi-C data via a global background model. 10.1101/2023.03.01.530686
• [75]  Ronen, J. & Akalin, A. (2018). netSmooth: Network-smoothing based imputation for single cell RNA-seq. F1000 Research. 7, 8. 10.12688/f1000research.13511.3
• [76]  He, Z. & Dony, L. & Fleck, J. S. & Szałata, A. & Li, K. X. & Slišković, I. & Lin, H.-C. & Santel, M. & Atamian, A. & Quadrato, G. & Sun, J. & Paşca, S.P. & Camp, J.G. & Theis. F. & Treutlein, B. (2023). An integrated transcriptomic cell atlas of human neural organoids. bioRxivm 10.1101/2023.10.05.561097
• [77]  Venkatasubramanian, M. & Chetal, K. & Schnell, D.J. & Atluri, G. & Salomonis, N. (2020). Resolving single-cell heterogeneity from hundreds of thousands of cells through sequential hybrid clustering and NMF. Bioinformatics, 36(12), 3773-3780. 10.1093/bioinformatics/btaa201
• [78]  Nagai, J.S. & Leimkühler, N.B. & Schaub, M.T. & Schneider, R.K. & Costa, I.G. (2021). CrossTalkeR: analysis and visualization of ligand-receptorne tworks. Bioinformatics, 37(22), 4263-4265. 10.1093/bioinformatics/btab370
• [79]  Browaeys, R. & Saelens, W. & Saeys, Y. (2020). NicheNet: modeling intercellular communication by linking ligands to target genes. Nature Methods, 17(2), 159-162. 10.1038/s41592-019-0667-5
• [80]  Tsuyuzaki, K. & Nikaido, I. (2017/12/24). Biological Systems as Heterogeneous Information Networks: A Mini-review and Perspectives. HeteroNAM’18, arXiv:1712.08865
• [81]  Sun, Y. & Han, J. (2012/7/23). Mining Heterogeneous Information Networks: Principles and Methodologies, Morgan & Claypool Publishers
• [82]  Noori, A. & Li, M.M. & Tan, A.L.M. & Zitnik, M. (2023). Metapaths: similarity search in heterogeneous knowledge graphs via meta-paths. Bioinformatics. 39(5), btad297. 10.1093/bioinformatics/btad297
• [83]  Valdeolivas, A. & Tichit, L. & Navarro, C. & Perrin, S. & Odelin, G. & Levy, N. & Cau, P. & Remy, E. & Baudot, A. (2019). Random walk with restart on multiplex and heterogeneous biological networks. Bioinformatics, 35(3), 497-505. 10.1093/bioinformatics/bty637
• [84]  Wen, Y. & Song, X. & Yan, B. & Yang, X. & Wu, L. & Leng, D. & He, S. & Bo, X. (2021). Multi-dimensional data integration algorithm based on random walk with restart. BMC Bioinformatics, 22(1), 97. 10.1186/s12859-021-04029-3
• [85]  Baptista, A. & Brière, G. & Baudot, A. (2024). Random walk with restart on multilayer networks: from node prioritisation to supervised link prediction and beyond. BMC Bioinformatics. 25(1), 70. 10.1186/s12859-024-05683-z
• [86]  Ding, H. & Yang, Y. & Xue, Y. & Seninge, L. & Gong, H. & Safavi, R. & Califano, A. & Stuart, J.M. (2020). Prioritizing transcriptional factors in gene regulatory networks with PageRank. iScience, 24(1), 102017. 10.1016/j.isci.2020.102017
• [87]  Yan, Y. & Bian, Y. & Luo, D. & Lee, D. & Zhang, X. (2019). Constrained Local Graph Clustering by Colored Random Walk. In The World Wide Web Conference (WWW ’19). Association for Computing Machinery, 2137-2146. 10.1145/3308558.3313719
• [88]  Tang, J. & Chang, Y. & Aggarwal, C. & Liu, H. (2016). A Survey of Signed Network Mining in Social Media. ACM Comput. Surv. 49, 3, 42, 37 pages. 10.1145/2956185
• [89]  J. Jung, W. Jin, L. Sael and U. Kang, (2016). Personalized Ranking in Signed Networks Using Signed Random Walk with Restart, IEEE 16th International Conference on Data Mining (ICDM), 973-978. 10.1109/ICDM.2016.0122
• [90]  Kunegis, J. & Schmidt, S. & Lommatzsch, A. & Lerner, J. & De Luca, E.W. & Albayrak, S. (2010) Spectral Analysis of Signed Graphs for Clustering, Prediction and Visualization. Proceedings of the 2010 SIAM International Conference on Data Mining (SDM). 559-570
• [91]  Fang, L., Yang, Q., Wang, J., Lei, W. (2016). Signed Network Label Propagation Algorithm with Structural Balance Degree for Community Detection. In: Chang, C., Chiari, L., Cao, Y., Jin, H., Mokhtari, M., Aloulou, H. (2016). (eds) Inclusive Smart Cities and Digital Health. ICOST 2016. Lecture Notes in Computer Science, 9677. 10.1007/978-3-319-39601-9_38
• [92]  Chen, X. & Zhang, D.H. & You, Z.H. (2018). A heterogeneous label propagation approach to explore the potential associations between miRNA and disease. Journal of Translational Medicine, 16(1), 348. 10.1186/s12967-018-1722-1
• [93]  Wang, H. & Huang, F. & Xiong, Z. & Zhang, W. (2022). A heterogeneous network-based method with attentive meta-path extraction for predicting drug-target interactions. Briefings in Bioinformatics, 23(4), bbac184. 10.1093/bib/bbac184
• [94]  Fu, G. & Ding, Y. & Seal, A. & Chen, B. & Sun, Y. & Bolton, E. (2016). Predicting drug target interactions using meta-path-based semantic network analysis. BMC Bioinformatics, 17, 160. 10.1186/s12859-016-1005-x
• [95]  Li, Y. & Qiao, G. & Gao, X. & Wang, G. (2022). Supervised graph co-contrastive learning for drug-target interaction prediction. Bioinformatics, 38(10), 2847-2854. 10.1093/bioinformatics/btac164
• [96]  Tanvir, F. & Islam, M.I.K. & Akbas, E. (2021). Predicting Drug-Drug Interactions Using Meta-path Based Similarities, 2021 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), 1-8, 10.1109/CIBCB49929.2021.9562802
• [97]  Hu, B. & Wang, H. & Yu, Z. (2019). Drug Side-Effect Prediction Via Random Walk on the Signed Heterogeneous Drug Network. Molecules. 24(20), 3668. 10.3390/molecules24203668
• [98]  Zhao, J. & Lv, C. & Wu, Q. & Zeng, H. & Guo, X. & Yang, J. & Tian, S. & Zhang, W. (2019). Computational systems pharmacology reveals an antiplatelet and neuroprotective mechanism of Deng-Zhan-Xi-Xin injection in the treatment of ischemic stroke. Pharmacol Res. 104365. 10.1016/j.phrs.2019.104365
• [99]  Liu, W. & Tang, T. & Lu, X. & Fu, X. & Yang, Y. & Peng, L. (2023). MPCLCDA: predicting circRNA-disease associations by using automatically selected meta-path and contrastive learning. Briefings in Bioinformatics, 24(4), bbad227. 10.1093/bib/bbad227
• [100]  　Wei, M.M. & Yu, C.Q. & Li, L.P. & You, Z.H. & Wang, L. (2023). BCMCMI: A Fusion Model for Predicting circRNA-miRNA Interactions Combining Semantic and Meta-path. Journal of Chemical Information and Modeling, 63(16), 5384-5394. 10.1021/acs.jcim.3c00852
• [101]  　Lu, C. & Zhang, L. & Zeng, M. & Lan, W. & Duan, G. & Wang, J. (2023). Inferring disease-associated circRNAs by multi-source aggregation based on heterogeneous graph neural network. Briefings in Bioinformatics, 24(1), bbac549. 10.1093/bib/bbac549
• [102]  　Chen, L. & Zhao, X. (2023). PCDA-HNMP: Predicting circRNA-disease association using heterogeneous network and meta-path. Mathematical Biosciences and Engineering, 20(12), 20553-20575. 10.3934/mbe.2023909
• [103]  　Luo, J. & Huang, C. & Ding, P. (2016). A Meta-Path-Based Prediction Method for Human miRNA-Target Association. BioMed Research International, 7460740. 10.1155/2016/7460740
• [104]  　Zhang, L. & Liu, B. & Li, Z. & Zhu, X. & Liang, Z. & An, J. (2020). Predicting MiRNA-disease associations by multiple meta-paths fusion graph embedding model. BMC Bioinformatics, 21(1), 470. 10.1186/s12859-020-03765-2
• [105]  　Liu, B. & Zhu, X. & Zhang, L. & Liang, Z. & Li, Z. (2021). Combined embedding model for MiRNA-disease association prediction. BMC Bioinformatics, 22(1), 161. 10.1186/s12859-021-04092-w
• [106]  　Yu, L. & Zheng, Y. & Gao, L. (2022). MiRNA-disease association prediction based on meta-paths. Briefings in Bioinformatics, 23(2), bbab571. 10.1093/bib/bbab571
• [107]  　Zhang, W. & Johnson, N. & Wu, B. & Kuang, R. (2012). Signed network propagation for detecting differential gene expressions and DNA copy number variations. In Proceedings of the ACM Conference on Bioinformatics, Computational Biology and Biomedicine (BCB ’12). 10.1145/2382936.2382979
• [108]  　Long, Y. & Wu, M. & Liu, Y. & Kwoh, C.K. & Luo, J. & Li, X. (2020). Ensembling graph attention networks for human microbe-drug association prediction. Bioinformatics, 36(Suppl_2), i779-i786. 10.1093/bioinformatics/btaa891
• [109]  　Jin, Y. & Ji, W. & Shi, Y. & Wang, X. & Yang, X. (2023). Meta-path guided graph attention network for explainable herb recommendation. Health Information Science and Systems, 11(1), 5.10.1007/s13755-022-00207-6
• [110]  　Kolda, T.G. & Bader, B.W. & Kenny, J.P. (2005). Higher-order Web link analysis using multilinear algebra, Fifth IEEE International Conference on Data Mining (ICDM’05), 8, 10.1109/ICDM.2005.77
• [111]  　Papalexakis, E.E. & Faloutsos, C. & Sidiropoulos, N.D. (2017). Tensors for Data Mining and Data Fusion: Models, Applications, and Scalable Algorithms. ACM Trans. Intell. Syst. Technol. 8, 2, 16, 44. 10.1145/2915921
• [112]  　Murakami, T. & Kanemura, A. & Hino, H. (2015). Group Sparsity Tensor Factorization for De-anonymization of Mobility Traces, 2015 IEEE Trustcom/BigDataSE/ISPA, 621-629, 10.1109/Trustcom.2015.427
• [113]  　Takai, Y. & Miyauchi, A. & Ikeda, M. & Yoshida, Y. (2020). Hypergraph Clustering Based on PageRank, arXiv, 10.48550/arXiv.2006.08302
• [114]  　Wang, C. & Shi, J. & Cai, J. & Zhang, Y. & Zheng, X. & Zhang, N. (2022). DriverRWH: discovering cancer driver genes by random walk on a gene mutation hypergraph. BMC Bioinformatics, 23(1), 277. 10.1186/s12859-022-04788-7
• [115]  　Wang, Q. & Yan, G. (2020). HRWR: Predicting Potential Efficacious Drug Combination Based on Hypergraph Random Walk with Restart. bioRxiv, 10.1101/2020.12.10.420760
• [116]  　Xie, G. & Zhu, Y. & Lin, Z. & Sun, Y. & Gu, G. & Li, J. & Wang, W. (2022). HBRWRLDA: predicting potential lncRNA-disease associations based on hypergraph bi-random walk with restart. Molecular Genetics and Genomics, 297(5), 1215-1228. 10.1007/s00438-022-01909-y
• [117]  　Niu, Y.W. & Qu, C.Q. & Wang, G.H. & Yan, G.Y. (2019). RWHMDA: Random Walk on Hypergraph for Microbe-Disease Association Prediction. Frontiers in Microbiology, 10, 1578. 10.3389/fmicb.2019.01578
• [118]  　Qionghai, Dai. & Yue, Gao. (2023/5/16). Hypergraph Computation (Artificial Intelligence: Foundations, Theory, and Algorithms). Springer
• [119]  　Wu, T. & Benson, A.R. & Gleich, D.F. (20XX). General Tensor Spectral Co-clustering for Higher-Order Data. NIPS 2016
• [120]  　Liqun, Qi. & Haibin, Chen. & Yannan, Chen. (2018/4/17). Tensor Eigenvalues and Their Applications (Advances in Mechanics and Mathematics, 39). Springer
• [121]  　Benson, A. & Gleich, D. (2018). Tensor eigenvectors and stochastic processes. SIAM ALA 2018, https://www.cs.cornell.edu/~arb/tesp/
• [122]  　Benson, A.R. & Gleich, D.F. & Lim, L.-H. (2016). The Spacey Random Walk: A Stochastic Process for Higher-Order Data. arXiv, 10.48550/arXiv.1602.02102
• [123]  　Kolda, T.G. & Mayo, J.R. (2011). Shifted Power Method for Computing Tensor Eigenpairs. arXiv, 10.48550/arXiv.1007.1267
• [124]  　Gleich, D.F. & Lim, L.-H. & Yu, Y. (2014). Multilinear PageRank, arXiv, 10.48550/arXiv.1409.1465
• [125]  　Cai, H. & Zheng, V.W. & Chang, K.C.-C. (2018). A Comprehensive Survey of Graph Embedding: Problems, Techniques and Applications, arXiv, 10.48550/arXiv.1709.07604
• [126]  　Xu, M. (2020). Understanding Graph Embedding Methods and Their Applications. arXiv, 10.48550/arXiv.2012.08019
• [127]  　Chen, Z.H. & You, Z.H. & Guo, Z.H. & Yi, H.C. & Luo, G.X. & Wang, Y.B. (2020). Prediction of Drug-Target Interactions From Multi-Molecular Network Based on Deep Walk Embedding Model. Frontiers in Bioengineering and Biotechnology. 8, 338. 10.3389/fbioe.2020.00338
• [128]  　Zhao, B.W. & You, Z.H. & Hu, L. & Guo, Z.H. & Wang, L. & Chen, Z.H. & Wong, L. (2021). A Novel Method to Predict Drug-Target Interactions Based on Large-Scale Graph Representation Learning. Cancers (Basel), 13(9), 2111. 10.3390/cancers13092111
• [129]  　Song, X.Y. & Liu, T. & Qiu, Z.-Y. & You, Z.-H. & Sun, Y. & Jin, L.-T. & Feng, X.-B. & Zhu, L. (2020). Prediction of lncRNA-Disease Associations from Heterogeneous Information Network Based on DeepWalk Embedding Model. In: Huang, DS., Premaratne, P. (eds) Intelligent Computing Methodologies. ICIC 2020. Lecture Notes in Computer Science, 2465. 10.1007/978-3-030-60796-8_25
• [130]  　Jindal, L. & Sharma, A. & Prasad, K.D. V. & Irshad, A. & Rivera, R. &Karimovna, A.D. (2023). A machine learning method for predicting disease-associated microRNA connections using network internal topology data, Healthcare Analytics, 4, 100215, 10.1016/j.health.2023.100215
• [131]  　Stassen, S.V. & Kobashi, M. & Huang, Y. & Ho, J.W.K. & Tsia, K.K. (2024). StaVia: Spatially and temporally aware cartography with higher order random walks for cell atlases. 10.1101/2024.01.29.577871
• [132]  　片山俊明＆川島秀一（2017/5/23）．生命医科学RDFデータの機械学習・人工知能への応用―Application of Machine Learning and Artificial Intelligence Methods for Biomedical RDF Data―，2017年度人工知能学会全国大会（第31回）
• [133]  　Wang, X. & Bo, D. & Shi, C. & Fan, S. & Ye, Y. & Yu, P.S. (2020). A Survey on Heterogeneous Graph Embedding: Methods, Techniques, Applications and Sources, arXiv, 10.48550/arXiv.2011.14867
• [134]  　Gonçalves, J.P. & Aires, R.S. & Francisco, A.P. & Madeira, S.C. (2012). Regulatory Snapshots: integrative mining of regulatory modules from expression time series and regulatory networks. PLoS One, 7(5), e35977. 10.1371/journal.pone.0035977
• [135]  　Qiu, J. & Dong, Y. & Ma, H. & Li, J. & Wang, K. & Tang, J. (2018/2/2). Network Embeddings as Matrix Factorization: Unifying DeepWalk, LINE, PTE, and node2vec, WSDM’18, 459-467. 10.1145/3159652.3159706
• [136]  　岩田具治．（015/4/8）．トピックモデル（機械学習プロフェッショナルシリーズ）．講談社
• [137]  　Ding, C. & He, X. & Simon, H, D. (2005). On the Equivalence of Nonnegative Matrix Factorization and Spectral Clustering. Proceedings of the 2005 SIAM International Conference on Data Mining (SDM). 2005, 606-610
• [138]  　Schubert, E. & Hess, S. & Morik, K. (2018). The relationship of DBSCAN to matrix factorization and spectral clustering. In LWDA 2018 - Lernen, Wissen, Daten, Analysen 2018: Proceedings of the conference Lernen, Wissen, Daten Analysen (pp. 330-334). (CEUR workshop proceedings; Vol. 2191). RWTH Aachen.
• [139]  　Vanluyten, B. & Willems, J.C. & Moor, B.D. (2008). Structured nonnegative matrix factorization with applications to hidden Markov realization and clustering, Linear Algebra and its Applications, 429(7), 1409-1424, 10.1016/j.laa.2008.03.010
• [140]  　Leby, O. & Goldberg, Y. (2014). Neural Word Embedding as Implicit Matrix Factorization, NIPS 2014
• [141]  　Liu, Z. & Liu, Q. & Zhang, H. & Zhu, J. (2023). Unifying Graph Convolutional Networks as Matrix Factorization. ICLR 2020 Conference

略語リスト

・EVD

Eigen Value Decomposition

・IRLBA

Augmented implicitly restarted Lanczos bidiagonalization methods

・IRAM

Implicitly Restarted Arnoldi Method

・PCA

Principal Component Analysis

・CCA

Canonical Correlation Analysis

・CA

Correspondence Analysis

・SVD

Singular Value Decomposition

・PPR

Personalized PageRank

・RWR

Random Walk with Restart

・MCL

Markov Clustering

・LEM

Laplacian Eigenmaps

・GBA

Guilt-By-Association

・PPI

Protein-Protein Interaction

・GRN

Gene Regulatory Network

・GWAS

Genome-wide Association Study

・HIN

Heterogenous Information Network

・RDF

Resource Description Framework

著者略歴

露崎 弘毅 2015年、東京理科大学生命創薬科学科博士後期課程終了。博士（薬科学）。同年より、理化学研究所（所属3）に在籍し、シングルセルオミックスのデータ解析や解析ツール開発に従事。現在は千葉大学（所属1、2）で医療データの解析を行なっている。パッケージングに特化したハッカソンBio“Pack”athonを主催。 ホームページ：https://researchmap.jp/kokitsuyuzaki