2014 年 30 巻 2 号 p. 132-140
2014 年 30 巻 2 号 p. 132-140
古来より、ギャンブル(賭博)は人間の生活とともにあり、遊戯・娯楽として、また近年では依存などの社会問題として、様々な領域や業界でしばしば話題に取り上げられてきている(帚木,2011)。従来、こうしたギャンブルについては、様々な心理学的研究が行われてきた。例えば、ギャンブル接触の実態調査を行った研究(Blinn-Pike, Worthy, & Jonkman, 2010; 品川,2010)をはじめ、パーソナリティ特性との関連を検討した研究(Bagby, Vachon, Bulmash, Toneatto, Quilty, & Costa, 2007; 高田・湯川,2011)、ギャンブル中の反応や行動に関する研究(高田・湯川,2012; Wölfling, Mörsen, Duven, Albrecht, Grüsser, & Flor, 2011)、あるいは、病的賭博(pathological gambling)に関する研究(Back, Lee, & Stinchfield, 2011; Lesieur & Custer, 1984)などである。これらの研究はそれぞれ、明らかにしようとしている側面(研究目的)という観点から、大きく三つのカテゴリーに分けることが可能である。すなわち、“ギャンブル以前(どのくらいの人が、あるいはどのような人がギャンブルをするのか)”、“ギャンブル過程(ギャンブルの最中にどのように反応あるいは行動するのか)”、“ギャンブル以後(なぜまたしたくなるのか、あるいはなぜやめられないのか)”の三つのカテゴリーである。本研究では、この中でも特に、ギャンブル中の反応や行動といった“ギャンブル過程”に焦点を当て、ギャンブルの基礎的行動メカニズムとその影響要因を実験的に検討することを目的とする。
一般に、賭博者の錯誤(gambler's fallacy)などの現象があるように、時として人はギャンブルに際して誤った推論に基づいた行動をすることが知られている。ギャンブルには、その不可欠な目的として“価値ある物(財物など)を獲得する”という目的があり、それなくしてはギャンブルと定義しえない(谷岡,1997)。確率的に考えれば、その目的を達成するためには、少しでも勝つ確率(あるいは期待値)が高い賭けをすることが要求され、損失を回避するためには、そもそもギャンブルをしない方が合理的であると考えられる。しかし、現実にギャンブルをする人は数多く存在し、勝つ確率(あるいは期待値)の低い大穴に賭けるギャンブラーも存在する。このように、なぜ人はギャンブルをするのか、そして、なぜ非合理的な賭けを行うのであろうか。
ギャンブル場面における非合理的な行動の最たるものとして、無謀なギャンブル行動(reckless gambling)が挙げられる。なお、本研究では、無謀なギャンブル行動を“ギャンブル場面において、結果的に損をする可能性がより大きい選択、すなわち期待値がより低い選択をすること”と定義する1)。無謀なギャンブル行動は、期待値が低いため、“価値ある物を獲得する”というギャンブルの目的に沿えば、本来避けられるべきものである。しかしながら、先述の定義に該当するような、度を越した賭けを行うギャンブラーの存在は広く知られており(Walker, 1992)、なぜこのような行動が生じるのか、いまだ十分に解明されていない。
これまでの先行研究の結果から、ギャンブルにおける勝敗とギャンブル中の感情状態が無謀なギャンブル行動と関連のあることが示されている(Cummins, Nadorff, & Kelly, 2009; 高田・湯川,2012)。Cummins et al.(2009)は、Acey–Deucey課題というトランプの出目に賭けるギャンブル課題を用いた実験研究を行った。実験では、30試行で構成される1セッションを2セッション行い(すなわち、前半後半に分け、計60試行行い)、前半で勝つ(負ける)試行数を操作することによって、前半の総合結果として勝ちが多い条件(80%の試行で勝ち)か負けが多い条件(20%の試行で勝ち)のいずれかを経験するようにした。また、Acey–Deucey課題では、勝つ確率が50%未満である試行と、勝つ確率が50%以上である試行とがあり、Cummins et al.(2009)では、勝つ確率が50%未満である試行で参加者が賭けた額を無謀な賭けの程度を示す指標とした。その結果、(前半の試行で)勝ちが多い条件の方が、(前半の試行で)負けが多い条件よりも、後半のセッション中、無謀な賭けを行っていたことが示された。さらに、Cummins et al.(2009)は、PANAS(Positive and Negative Affect Schedule; Watson, Clark, & Tellegen, 1988)を用いて、二つのセッションの間での参加者の感情状態についても測定した。その結果、(前半の試行で)勝ちが多い条件の方が、(前半の試行で)負けが多い条件よりも、有意に快感情を喚起していたことが示された。また、快感情と後半の課題における無謀な賭けの程度(勝つ確率が50%未満の試行での賭けの額)との間に有意な正の相関が見られ、逆に、手堅い賭けの程度(勝つ確率が50%以上の試行での賭けの額)との間に有意な負の相関が見られた。なお、前半の勝敗および快感情を説明変数とし、後半の課題における無謀な賭けの程度を目的変数とした重回帰分析を行ったところ、勝敗の効果は有意であったが、快感情は有意傾向にとどまった。
高田・湯川(2012)は、Game of Dice Task(Brand, Fujiwara, Borsutzky, Kalbe, Kessler, & Markowitsch, 2005)というサイコロの出目に賭けるギャンブル課題を用いて、大学生を対象とした実験研究を行った。実験は、18試行からなるセッションを2セッション行った。また、分析では、1試行ごとの勝敗が次の賭け行為に及ぼす影響の検討を行った。その結果、Cummins et al.(2009)によるセッション全体の総体的な分析結果と同様、1試行ごとの賭け行為においても、勝った後の方が負けた後よりも、後続する選択が相対的に無謀なものになりやすいということが示された。さらに、高田・湯川(2012)は、日本語版PANAS(佐藤・安田,2001)を用いて、ギャンブル課題のセッション前後およびセッション間の感情状態を測定し、無謀なギャンブル行動との関連を検討した。その結果、勝敗と感情状態との間に有意な関連は見られず、勝ちを経験することによって快感情が喚起されるというCummins et al.(2009)の結果とは一致しなかった。なお、各セッションでの無謀なギャンブル行動とセッション間の快感情との間には、有意な正の相関が見られた。
ここで、ギャンブル行動は、選択時に確率判断を要することから、リスク判断とも関連していると考えられる。感情状態とリスク判断の関連に関して、快感情によって、楽観的なリスク判断がされるという知見(Johnson & Tversky, 1983; Nygren, Isen, Taylor, & Dulin, 1996)がある一方、それとは逆に、快感情によってリスク回避的に、不快感情によってリスク愛好的になるという結果も報告されている(Leith & Baumeister, 1996; Mittal & Ross, 1998)。さらに、Isen & Patrick(1983)は、快感情が喚起されると、ローリスクの選択肢ではリスク愛好的になり、ハイリスクの選択肢ではリスク回避的になることを示し、選択肢のリスクの程度によって、感情状態の影響が異なるという可能性を示唆した。しかしながら、これらの研究では、人間のギャンブル行動のメカニズムの解明に焦点を当てておらず、必ずしも実験的にギャンブル行動を測定しているわけではない。ギャンブル行動と感情状態との関連を明らかにするため、より現実場面に即した形でギャンブル行動の測定を行った上で、これらの関連について、検討し直す必要があると考えられる。
また、Wohl & Enzle(2003)は、ギャンブル行動に影響を及ぼす要因として、自己の運の良し悪しの知覚(self-perceived personal luck;以下、運の知覚)を扱っている。Wohl & Enzle(2003)は、ギャンブル課題としてパソコン画面上でのルーレットを用い、大きな損失を回避した状況(near big loss)と大きな利得を逃した状況(near big win)のいずれかを参加者に経験させて自己の運の知覚の操作を行い、その後の試行でどちらの方が賭けるチップの額が多いかを検討した。その結果、運が良いと知覚している参加者、すなわち大きな損失を回避した状況(near big loss)の方が、後の試行で有意に多くの額を賭けていた。このWohl & Enzle(2003)の結果から、人は“自分は運が良い”と知覚しているときとそうでないときとで、ギャンブル場面における行動に差異があるということが示唆された。
さらに、運の知覚と賭博者の錯誤(gambler's fallacy)との関連について、自分は運が良いと知覚している人ほど良い結果が続く自信を持つのに対し、自分は運が悪いと知覚している人ほど良い結果が続く自信を持たないということが示唆されている(Darke & Freedman, 1997)。また、プロスペクト理論(Kahneman & Tversky, 1979; Tversky & Kahneman, 1992)の確率加重関数の考え方によれば、そもそも人は実際に起こる確率が非常に低い現象(例;宝くじの1等、競馬の大穴)に対して、それが生起する確率を実際の客観的な確率よりも過大に見積もる傾向があるという。それに加えて、運(の良さ)を知覚することによって、勝つ確率をより過大評価してしまい、合理的ではないギャンブル行動が引き起こされるという可能性が考えられる。
このように、ギャンブル行動、特に賭けの無謀さ・手堅さに影響を及ぼす要因として、勝敗、感情状態、運の知覚が挙げられる。しかし、それぞれの関連性を考えた場合、いずれの要因が無謀なギャンブル行動との関連が強いか、また、どのようなメカニズムが生じているのかなど、十分に検討されているとはいい難い。これまでの研究から、勝敗が感情状態・運の知覚の変化に影響すること、感情状態・運の知覚と無謀なギャンブル行動が関連することが示されている。その中で、Cummins et al.(2009)は、快感情よりも勝敗の方が後続する賭けを予測することを示し、Wohl & Enzle(2003)では、賭けの結果によって生じた運の知覚の上昇が、後続する賭けに影響していたことを示している。また、高田・湯川(2012)は、二つのセッションの間の快感情と後半のセッションの無謀なギャンブル行動との間に、有意な正の相関が見られたことを示している。ここから、勝敗によって生じる感情状態と運の知覚の変化が媒介し、無謀なギャンブル行動を予測するという過程が生じている可能性が考えられる。
このことを明らかにするため、本研究では、賭けを1試行行うごとに感情状態と運の知覚の測定を行い、勝敗およびギャンブル行動の無謀さ・手堅さとの関連の検討を行う。これまでの研究では、感情状態や運の知覚を、多数回の試行からなる課題の前後などでのみ測定しているため、1試行ごとの勝敗とそれに伴った感情状態と運の知覚の変化が及ぼす影響が、明確に検討されていない。そのような測定を行った場合、課題全体を通したギャンブル行動の結果との大枠での関連は検討することができるが、一つ一つの賭けが直接的に感情状態や運の知覚とどのように関連しているのかを知ることはできない。また、そのような大枠でのマクロな検討方法では、一つ一つの賭けの結果次第で動くミクロな変化を捉えきれない。これに対して、賭けの最小単位である1試行ごとに測定を行えば、実験参加者の賭けの結果(勝敗)に伴った状態の細かな変化まですくい取ることができ、勝敗、感情状態、運の知覚の影響についてより正確に検討することが可能となる。さらに、ギャンブル課題遂行中においては、実験参加者はそれぞれ様々な行動をとると考えられるが、1試行ごとの測定を行うことによって、それら全ての行動パターンにおける感情状態と運の知覚の変化を網羅的に検討できると考えられる。
また、ギャンブルにおける勝敗と感情状態との関連に関して、Cummins et al.(2009)では、勝つことによって快感情が喚起されることが示されたのに対し、高田・湯川(2012)では、勝敗と快感情との間に有意な関連は示されていない。この結果の不一致に関して、Cummins et al.(2009)では、感情状態の測定を二つのセッションの間に1回だけ行っており、高田・湯川(2012)では、二つのセッションの前後と間の計3回、感情状態を測定している。そこで、本研究では、1試行ごとに感情状態の測定を行うことで、勝敗と感情状態の測定の時間差を最小限とすることで、両者の関連性について、より正確に検討を行う。
以上より、本研究では、大学生を対象とした実験室実験を実施し、勝敗、感情状態、および運の知覚が、ギャンブル行動の無謀さ・手堅さにどのように影響を及ぼしているか、それぞれの関連性を踏まえ、検討することを目的とする。また、快感情が喚起されたとき、ローリスクの選択肢ではリスク愛好的になり、ハイリスクの選択肢ではリスク回避的になるというIsen & Patrick(1983)の知見を踏まえ、本研究では、直前の賭けの無謀さ・手堅さの程度を考慮した上で検討を行う。
実験参加者には、18試行からなる実験課題(ギャンブル課題)に取り組んでもらい、第1試行の前と各試行の後に、感情状態と運の知覚の測定を質問紙上で行った。したがって、感情状態と運の知覚の測定は、計19回行った。
実験参加者関東圏の国立大学に通う大学生42名(男性21名、女性21名、平均年齢19.67歳、SD=1.12)を対象とした。実験への参加は、大学の講義時間において募集を行うとともに、個別に協力を依頼した。
実験課題(Game of Dice Task: GDT)本研究では、ギャンブル課題として、Brand et al.(2005)のGame of Dice Task(以下、GDT)を用いた。本研究におけるGDTのプログラムは、Windows用プログラム言語HSP(Hot Soup Processor)を用いて、Brand et al.(2005)が開発したものと同様のものを製作した。Figure 1にGDTのサンプル画面を示した。
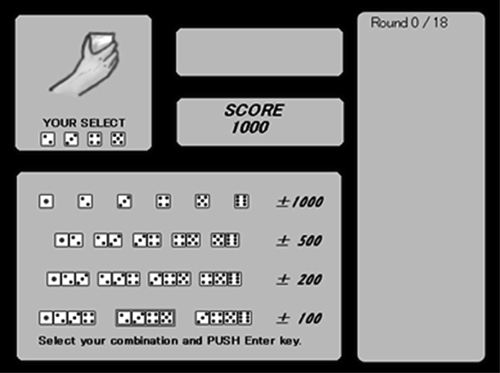
この課題は、コンピュータ画面上でサイコロの出る目を予想し、架空の元金1000点を最大化することが目的である。サイコロを振る各試行の前に、参加者はどの目が出るかを予想し、予想が当たったときには、画面上に“You Win”の文字が、外れたときには“You Lose”の文字が表示され、得点が加点あるいは減点された。この選択を1試行として、課題は18試行で構成された。課題遂行中、現時点での得点と残りの試行回数が常に画面上に表示された。また、選択時間に制限は設けなかった。GDTでは、選択肢の移動にカーソルキーを、決定にエンターキーを用いた。
各試行における予想の選択肢は以下のとおりであった。“1234”“2345”“3456”の四つの数字の組み合わせのいずれかを選択し、出た目が選択肢に含まれていた(すなわち、当たった、勝った)場合には+100、含まれていなかった(すなわち、外れた、負けた)場合には−100となる。“123”“234”“345”“456”の三つの数字の組み合わせのいずれかを選択し、当たった場合には+200、外れれば−200となる。“12”“23”“34”“45”“56”の二つの数字の組み合わせのいずれかを選択し、当たった場合には+500、外れれば−500となる。“1”“2”“3”“4”“5”“6”の一つの数字のいずれかを選択し、当たった場合には+1000、外れれば−1000となる。このように、当たる確率が低い選択肢ほど、加点あるいは減点される得点が大きくなる。したがって、GDTにおいては、各選択肢の期待値が33.3、0、−166.7、−666.7と幾何級数的に大きく異なっている。そのため、各選択肢を比較した場合、当たる確率が低い選択肢ほど、相対的に期待値が大幅に低くなる“無謀な”選択となっている。
このように、GDTは各選択肢の期待値が大きく異なっており、賭け行為の無謀さ・手堅さをより明確に測定することが可能である。さらに、GDTは客観的な勝つ確率と増減する得点が、18試行を通して選択肢ごとに固定されているため、1試行ごとの勝敗が次の選択に与える影響の検討に適していると考えられる。以上の理由から、本研究では実験課題としてGDTを用いた。
評定用紙ギャンブル課題中の参加者の感情状態、運の知覚の程度を測定するために、19枚からなる冊子体の評定用紙を参加者に渡し、GDTの第1試行前とGDTを1試行行うごとに、1枚ずつめくりながら手書きで回答するよう求めた。評定用紙は、以下の二つの項目で構成された。
感情状態の測定参加者の感情状態を測定するために、Affect Grid(Russell, Weiss, & Mendelsohn, 1989)を用いた。これは、9×9の81マスの正方形の格子を配置した空間上で、現在の感情状態を評価するものである。格子の横軸は快–不快(pleasure–displeasure)次元であり、9点が快(Pleasant)、1点が不快(Unpleasant)を意味する。格子の縦軸は活性–不活性(arousal–sleepiness)次元であり、9点が活性(High Arousal)、1点が不活性(Sleepiness)を意味する。Russell et al.(1989)にならい、本研究では、快–不快次元の得点を“快得点(pleasure score)”、活性–不活性次元の得点を“活性得点(arousal score)”と称する。快得点および活性得点ともに5点が普段の感情状態を表し、得点が高いほど“快”あるいは“活性”が高い状態であるということを意味する。Affect Gridでは、従来の質問紙法と比較して評定者の負担を軽減することが可能であるため、試行ごとの感情状態の測定に適していると考えられる。また、Affect Gridの信頼性、妥当性は十分に検討されている(Russell et al., 1989)。Affect Gridの回答方法に関して、参加者には、“あなたの現在の気分状態に当てはまるところに、×で記して評価して下さい”と教示した。
運の知覚の測定参加者の運の知覚の程度を測定するために、1項目の質問(今、あなたはどのくらい運がいいと思いますか?)を用いた。回答は11件法であり、得点が高いほど、自己の運を高く知覚しているということを意味した(−5:運が悪い、+5:運がいい)。以後、本研究では、この得点を“運得点”と称する。
手続き参加希望者が実験室に来室した際、はじめに、(a)実験内容、(b)心身への影響、(c)参加の自由、(d)参加の拒否・辞退、(e)個人情報の保護について十分に説明した上で、実験参加同意書への署名を得た。なお、同意を求める際、最終的に課題の得点がプラスであった場合には、その額に応じた分の謝礼が、マイナスであった場合には、その額に応じたペナルティがある、という架空の教示を行った。具体的には、得点がプラスの場合には点数分の額(日本円)の図書カードを謝礼として、マイナスの場合には時給1000円換算で点数分の額の時間、データ入力の手伝いをペナルティとして与えると説明した。例えば、ある参加者のGDTにおける最終的な得点が500点から900点であった場合、500円分の図書カードを謝礼とし、最終的な得点が−500点から−900点であった場合には、500円分すなわち30分相当のデータ入力をペナルティとして与えると教示した。
実験参加の同意が得られた後、評定用紙の回答方法について説明を行った。その後、GDTの操作方法について具体的に説明を行い、さらに練習試行としてGDTを2試行体験させることで、操作方法を十分に理解させた。練習試行終了後、参加者に評定用紙を渡し、本試行を開始した。課題遂行中、実験者は参加者から見えない位置に控え、課題が終了したら声をかけるよう、参加者に求めた。
課題後、実験は終了したことを参加者に告げ、実験に関するデブリーフィングを行った。なお、口頭で確認したところ、参加者全員が謝礼を期待あるいはペナルティを覚悟していたが(42名のうち、得点が最終的にプラスとなった者は33名、マイナスとなった者は9名であり、平均得点とその標準偏差は430.95±2323.00であった)、得点分の謝礼もしくはペナルティはないことを説明した。その際、補足説明として、研究の目的、個人情報の保護、データの拒否・辞退について不利益を生じないことを改めて説明した。この手続きに関して、不服を申し立てた参加者は一人もいなかった。最後に、データ使用に関する同意書への署名を求め、参加者全員から同意を得た。なお、本研究は、筑波大学人間系研究倫理委員会の承認を得て実施された。
分析に先立ち、GDTの各試行における選択を次のように得点化した。“1234”“2345”“3456”の組み合わせのいずれかを選択した場合は1点、“123”“234”“345”“456”の組み合わせのいずれかを選択した場合は2点、“12”“23”“34”“45”“56”の組み合わせのいずれかを選択した場合は3点、“1”“2”“3”“4”“5”“6”のいずれかを選択した場合は4点とした。本研究では、この得点が高いほど、相対的に期待値が低くなるという意味において、無謀な選択であることを示していることから、これをReckless Gambling得点(以下、RG得点)と称した。また、GDTにおける勝った試行数の平均値は、18回中10.07(SD=3.54)であった。
データの基礎的検討GDTの最終的なスコア(得点)、快得点、活性得点、運得点のそれぞれの平均値は、430.95(SD=2323.00)、5.03(SD=1.76)、5.75(SD=1.64)、−0.30(SD=2.15)であった。性差の検定を行ったところ、男性よりも女性の方がGDTの最終的なスコアが有意に高かったが(t(40)=2.64, p<.05, d=0.81)、その他の変数においては有意な差が見られなかったため、以下の分析は性別を区分せずに行った。
勝敗が感情状態、運の知覚、ギャンブル行動の無謀さ・手堅さに及ぼす影響はじめに、ある試行で勝ったときあるいは負けたとき、感情状態と運の知覚にどのような影響を与えるのかを検討した。従属変数は、快得点・活性得点・運得点のそれぞれの“(ある得点)−(一つ前の得点)”とし、この差(変化量)が正であれば、得点が上昇したことを意味し、逆に、負であれば、得点が下降したことを意味する。この変化量に着目することで、個々の試行の勝敗を通して、試行の直前の状態から各得点がどの程度増減したかについて、より正確に検討することができると考えられる。本分析は、直前の賭けの無謀さ・手堅さ(直前の試行のRG得点)を考慮せずに行った。756回分(18回×42名分)の素データに関して、勝った場合と負けた場合の各得点の変化量の平均値と標準偏差をTable 1に示した。勝敗を独立変数、各得点の平均変化量を従属変数としたt検定を行ったところ、いずれも有意な差が見られた(快:t(750)=14.87, p<.01, d=1.10;活性:t(750)=5.00, p<.01, d=0.36;運:t(744)=15.03, p<.01, d=1.13)。すなわち、勝った後の方が負けた後よりも各得点が相対的により上昇することが示された2)。
| 快得点 | 活性得点 | 運得点 | ||||
|---|---|---|---|---|---|---|
| 勝ち | 負け | 勝ち | 負け | 勝ち | 負け | |
| 平均値 | 0.62 | −0.85 | 0.20 | −0.18 | 0.48 | −0.66 |
| 標準偏差 | 1.18 | 1.52 | 0.88 | 1.24 | 0.93 | 1.11 |
次に、ある試行で勝ったときあるいは負けたとき、次の選択にどのような影響を与えるのかを検討した。714試行分(17試行×42名分)の素データに関して、直前の試行のRG得点ごとに3)、勝った場合と負けた場合の次の試行のRG得点をTable 2に示した。Table 2にあるとおり、RG得点全体の分布を見ると、1点が376試行、2点が243試行であり、3点や4点を選択した試行数(計95試行)よりも極めて多かった。ここで、直前の勝敗の影響に関して、直前の試行のRG得点が1点の場合と2点の場合は、勝った後の方が負けた後よりも、次の試行のRG得点が2点である割合が大きく、1点である割合が小さかった。直前の試行のRG得点が3点の場合、勝った場合でも負けた場合でも次の試行のRG得点に大きな差は見られなかった。直前の試行のRG得点が4点の場合、そもそも合計の試行数が16試行と少ないものの、負けた場合の次の試行のRG得点が4点である割合が92.86%(14試行)と極めて大きかった。
| 直前の試行のRG得点(714試行) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1(376試行) | 2(243試行) | 3(79試行) | 4(16試行) | |||||
| 勝ち | 負け | 勝ち | 負け | 勝ち | 負け | 勝ち | 負け | |
| 1 | 198 (75.29) | 93 (82.30) | 28 (23.72) | 50 (40.00) | 1 (5.88) | 4 (6.45) | 0 (0.00) | 1 (7.14) |
| 2 | 60 (22.81) | 20 (17.70) | 79 (66.95) | 64 (51.20) | 4 (23.52) | 13 (20.97) | 0 (0.00) | 0 (0.00) |
| 3 | 4 (1.52) | 0 (0.00) | 11 (9.32) | 10 (8.00) | 11 (64.71) | 41 (66.13) | 1 (50.00) | 0 (0.00) |
| 4 | 1 (0.38) | 0 (0.00) | 0 (0.00) | 1 (0.80) | 1 (5.88) | 4 (6.45) | 1 (50.00) | 13 (92.86) |
| 合計試行数 | 263 | 113 | 118 | 125 | 17 | 62 | 2 | 14 |
| 平均値 | 1.27 | 1.18 | 1.86 | 1.70 | 2.71 | 2.73 | 3.50 | 3.79 |
| 標準偏差 | 0.50 | 0.38 | 0.56 | 0.65 | 0.69 | 0.68 | 0.71 | 0.80 |
括弧内の数字は、勝った場合あるいは負けた場合におけるそれぞれの合計試行数に占める%を示す。
勝敗を独立変数、次の試行のRG得点を従属変数とし、直前の試行のRG得点ごとにt検定を行ったところ4)、直前の試行のRG得点が1点の場合、有意傾向であるが、勝った後の方が負けた後よりも次の試行のRG得点が高かった(t(374)=1.76, p<.10, d=0.20)。直前の試行のRG得点が2点の場合、勝った後の方が負けた後よりも次の試行のRG得点が有意に高かった(t(241)=2.05, p<.05, d=0.26)。なお、直前の試行のRG得点が3点の場合と4点の場合には、有意な差は見られなかった(t(77)=−0.11, p>.10, d=0.03; t(14)=−0.48, p>.10, d=1.16)。ここから、比較的勝つ確率(期待値)が高い選択(直前の試行のRG得点が1点あるいは2点)をした次の選択においては、勝った後の方が負けた後よりも次の選択が手堅くなりにくく、比較的勝つ確率(期待値)が低い選択(直前の試行のRG得点が3点あるいは4点)をした次の選択においては、勝敗の影響を受けにくいということが示された5)。
勝敗、感情状態、および運の知覚がギャンブル行動の無謀さ・手堅さに及ぼす影響勝敗とそれに伴う感情状態および運の知覚の変化がギャンブル行動の無謀さ・手堅さに及ぼす影響の程度を検討するために、重回帰分析(ステップワイズ法)を行った。本分析では、1試行ごとの変化を検討するため、714試行分(17試行×42名分)の素データを用いた。ここで、本研究の素データは、複数の試行のデータが一人の実験参加者から得られているが、村上・石黒(2005)にならい、Stata Ver.13のclusterオプションを用いて、推定される回帰係数の標準誤差の調整を行った。また、本分析も、勝敗が次の選択に及ぼす影響の分析同様、直前の試行のRG得点ごとに行ったが、直前の試行のRG得点が3点、4点の場合については、試行数が少なく、勝敗の有意な影響が見られなかったため、分析の対象としなかった。
直前の試行の勝敗、快得点・活性得点・運得点の変化量を説明変数、次の試行のRG得点を目的変数とした重回帰分析(ステップワイズ法)を行ったところ、直前の試行のRG得点が1点の場合、次の試行のRG得点は、どの変数からも有意には予測されなかった。また、直前の試行のRG得点が2点の場合、次の試行のRG得点は、有意傾向であるが、勝敗(β=.20, p<.05, R2=.03, p<.10)によってのみ予測された。すなわち、勝った後の方が、RG得点が高かったことが示された。ここから、次の試行のRG得点の変化に対しては、感情状態や運の知覚に比べて勝敗の影響が相対的に大きいものであるということが示唆された。
本研究では、大学生を対象に、勝敗、感情状態、および運の知覚が、ギャンブル行動の無謀さ・手堅さに及ぼす影響について、実験によって検討した。分析の結果から、以下のことが示された。第一に、勝った後の方が負けた後よりも、快感情、活性状態、運の知覚が高まるということが示された。第二に、比較的勝つ確率(期待値)が高い選択(直前の試行のRG得点が1点あるいは2点)をした次の選択においては、勝った後の方が負けた後よりも次の選択が手堅くなりにくい(無謀になりやすい)ということが示された。なお、比較的勝つ確率(期待値)が低い選択(直前の試行のRG得点が3点あるいは4点)をした次の選択においては、勝敗の有意な影響は示されなかった。第三に、勝つ確率が50%(期待値が0)の選択(直前の試行のRG得点が2点)をした次の選択において、無謀な選択へのシフトは快感情、活性状態、運の知覚の上昇からは有意に予測されず、直前の結果(勝敗)によってのみ有意に予測された。
勝敗と感情状態との関連に関して、Cummins et al.(2009)では、前半の勝ちとセッション間の快感情との間に関連が見られ、一方、高田・湯川(2012)では、勝敗と快感情の間には有意な関連が見られなかったが、本研究で行った、1試行ごとの結果(勝敗)が1試行ごとの感情状態の変化に及ぼす影響の分析結果からは、勝った後の方が負けた後よりも、快感情が高まるということが示された。したがって現時点では、勝つことによって快感情が喚起されるとする方が妥当な結論であると考えられる。
高田・湯川(2012)との結果の不一致が生じた原因として、感情状態の測定方法が異なっていたという点が挙げられる。高田・湯川(2012)では、感情状態の測定方法として、二つのセッションの前後と間の計3回、いずれも同様の16項目からなる質問紙(PANAS)への回答を求めた。このような粗い測定を行った場合、参加者の感情状態は、ギャンブルの勝敗のみならず、捉えきれない様々な要因の影響を受ける可能性があり、勝敗と感情状態の関連を厳密に検討しているとはいえないと考えられる。なお、Cummins et al.(2009)においては、高田・湯川(2012)と同様、二つのセッションの間に質問紙(PANAS)で感情状態の測定を行ったが、課題前半の結果の操作を行うことで、勝敗の影響を際立たせていたため、勝敗と快感情との間に有意な関連が見られたのではないかと考えられる。本研究は1試行ごとに細かく測定を行って分析しており、その点で他の要因の影響を受けにくいため、勝った後は快感情が喚起されるという結論の妥当性は相対的にも高いといえる。
次に、直前の結果が次の選択に及ぼす影響に関して、本研究の結果は、先行研究(Cummins et al., 2009;高田・湯川,2012)の結果と一致するものであり、この現象の頑健性が示された。すなわち、ギャンブル過程における人間一般の行動として、勝った後の方が負けた後よりも、後の選択が相対的に無謀になりやすい(手堅くなりにくい)傾向があるということが確認された。なお、本研究では、比較的勝つ確率(期待値)が高い選択(直前の試行のRG得点が1点あるいは2点)をした次の選択においてのみ、次の選択への勝敗の有意な影響が示され、比較的勝つ確率(期待値)が低い選択(直前の試行のRG得点が3点あるいは4点)をした次の選択においては、勝敗の有意な影響は示されなかった。本研究で用いたGDTでは、期待値が非常に低い選択肢が設けられており、それらは、勝っても負けても1試行で増減する得点が大きくなっていた。例えば、RG得点が4点の選択肢では、増減する得点が最初の持ち点と同額である1000点であった。そのような選択肢を選ぶことは、勝敗にかかわらず、状況(持ち点)の変化が著しいため、勝敗の影響が生じにくかったのではないかと考えられる。なお、この結果は、快感情が喚起されると、ローリスクの選択肢ではリスク愛好的になり、ハイリスクの選択肢ではリスク回避的になるというIsen & Patrick(1983)の知見とも一致したものである。ここから、人間一般の行動として、特に勝つ確率が高い選択で勝った後において、賭けが無謀(あるいはリスク愛好的)になりやすいという可能性が示唆された。
また、勝敗とそれに伴う感情状態および運の知覚の変化が、ギャンブル行動の無謀さ・手堅さに及ぼす影響の程度を検討したところ、勝つ確率が50%(期待値が0)の選択(直前の試行のRG得点が2点)をした次の選択において、勝敗の直接の影響が相対的に強く、感情状態および運の知覚の有意な効果は示されなかった。本研究では、1試行ごとに感情状態と運の知覚の測定を行い、より正確にメカニズムの検討を行ったが、ギャンブル行動の無謀さ・手堅さに及ぼす影響は、そのような感情状態や運の知覚の変化以上に、勝敗が重要であったことが考えられる。
無謀なギャンブル行動に代表される、人の合理的とはいえない行動は、プロスペクト理論(Kahneman & Tversky, 1979; Tversky & Kahneman, 1992)の観点から説明することが可能である(竹村,2009)。人は、生起確率の低い事象に関して、その確率を過大評価する傾向がある。そして、このような確率の過大評価(楽観的判断)は、快感情を喚起しているときに、より顕著になると考えられる(Schwarz & Clore, 1983)。また、このような行動は、Langer(1975)が提唱した制御幻想(illusion of control)とも深く関連している(増田,2002)。制御幻想とは、運や偶然によって結果が決まる場面において、結果を自分でコントロールできるかのような錯覚を抱くことである。この幻想によって、客観的な確率が保証している以上に、不適切に高く成功確率を期待してしまうため、合理的でない行動をとってしまう。この制御幻想は、“自分は運が良い”と知覚しているときほど、それが顕著になるだろうと推測される。なお、本研究では、直前の試行の勝敗によってその変化が大きく規定されていたためか、ギャンブル行動の無謀さ・手堅さに及ぼす感情状態と運の知覚の有意な影響は示されなかった。相対的には、ギャンブル行動の無謀さ・手堅さに及ぼす勝敗の影響が大きいと考えられるものの、感情状態と運の知覚の影響をより明確に理解するためには、その影響を勝敗と切り離し、ギャンブルとは無関連に喚起された場合にどう影響するかなど、さらなる検討を行う必要がある。さらに、“今、自分は運が良い”と知覚すると同時に、“楽しい”“嬉しい”といった感情を喚起することは、現実場面においても十分考えられる。そのため、感情状態と運の知覚の相互(相乗)効果についても、今後検討していくことが望まれる。
また、活性状態の変化に関しても、ギャンブル行動の無謀さ・手堅さとの間には有意な関連は示されなかった。そもそも、ギャンブル過程において、人の活性状態は平時よりも全般的に上昇すると考えられる。今後は、本研究で扱った主観的な活性(覚醒)に加えて生理的な覚醒の影響も踏まえて、感情状態や運の知覚の影響とともに実証データを積み重ねる必要があるだろう。
最後に、本研究の限界と今後の展望について述べる。まず、限界点として本研究における実験参加者がすべて一般の大学生であったことが挙げられる。本研究で得られた知見が、病的賭博といった臨床群や、一般のギャンブル愛好者についても該当するのかどうか、対象者を拡大して検討する必要があると考えられる。次に、感情状態の測定方法として、本研究では参加者の自己報告による主観的な判断に依存していたことが挙げられる。本研究のように、賭けの結果が目の前に見える状況下で感情の自己報告を求めた場合、実際に喚起されている以上に、賭けの結果の影響を受けて感情状態が評定されていた可能性が考えられる。今後、生理的指標や潜在的指標などの主観によらない測定を行うことが望まれる。また、本研究では、ギャンブル行動の中でも特に無謀な賭けに焦点を当てて検討を行ったが、ギャンブル行動のその他の側面(例えば、賭けのスピードやギャンブルの継続意思など)に関しても、今後検討する必要があると考えられる。同様に、ギャンブル行動に影響すると考えられる、感情状態や運の知覚以外の要因(例えば、最終的に選択の意思決定をする高次の認知的判断など)にも注目する必要がある。これらの検討を系統的に行うことで、ギャンブルの基礎的行動メカニズムとその影響要因の理解をより深めることができるだろう。