Grain-Size Effects on Mechanical Behavior and Failure of Dense Cohesive Granular Materials

Abstract

The grain sizes can significantly influence the granular mechano-morphology, and consequently, the macro-scale mechanical response. From a purely geometric viewpoint, changing grain size will affect the volumetric number density of grain-pair interactions as well as the neighborhood geometry. In addition, changing grain size can influence initial stiffness and damage behavior of grain-pair interactions. The granular micromechanics approach (GMA), which provides a paradigm for bridging the grain-scale to continuum models, has the capability of describing the grain size influence in terms of both geometric effects and grain-pair deformation/dissipation effects. Here the GMA based Cauchy-type continuum model is enhanced using simple power laws to simulate the effect of grain size upon the volumetric number density of grain-pair interactions, and the parameters governing grain-pair deformation and dissipation mechanisms. The enhanced model is applied to predict the macroscopic response of cohesive granular solids under conventional triaxial tests. The results show that decreasing grain-sizes can trigger brittle-to-ductile transition in failure. Grain size is found to affect the compression/dilatation behavior as well as the post-peak softening/hardening of granular materials. The macro-scale failure/yield stress is also found to have an inverse relationship with grain-sizes in consonance with what has been reported in the literature.

1. Introduction

The macro-scale behaviors of dense cohesive granular materials are directly linked to the grain-scale through their granular mechano-morphology, which is represented by their collective arrangements (microstructure) and their interaction mechanisms (micromechanics). The mathematical description of macro-scale response of granular materials must begin from the conception of grain-interactions. From this point of departure, either discrete or continuum descriptions can be elaborated. In discrete models, the macro-scale behavior is inferred by tracking the motion of each grain in response to the external action. Continuum models, in contrast, aim to describe behavior at a spatial scale in which the grains and their motions remain concealed within a material point of a continuous system. While discrete analysis schemes can provide results with detailed description of grain motions, inter-granular deformations, they are limited in their applicability to large-scale problems due to large computational cost, and the challenges of grain-scale verification and validation. On the other hand, classical continuum models, while computationally affordable, suffer from losing characteristic features due to neglecting grain scale phenomena (in terms of both the microstructure and its evolution, as well as the inter-granular mechanisms). In this regards, it is noteworthy that higher-gradient continuum models represent a way to capture the effect of microstructure and its evolution during loading (Placidi L. and Barchiesi E., 2018; Placidi L. et al., 2018a; 2018b), an approach that can be traced to the early development in continuum mechanics (dell’Isola F. et al., 2014; Eugster S.R. and dell’Isola F., 2017).

Granular micromechanics approach (GMA) provides a paradigm that bridges the grain-scale models to appropriate continuum model (Nejadsadeghi N. and Misra A., 2020; Poorsolhjouy P. and Misra A., 2019). In this approach, the constitutive relation for a continuum material point is derived by utilizing the directional average of variously oriented grain-pairs. In this way, GMA incorporates data from the microstructure and micromechanical phenomena at grain scale into the continuum model (Misra A. et al., 2020). It has been shown that by incorporating the grain-pair interactions in different directions, GMA is able to capture various behavior, that are difficult to attain with classical continuum models, using computational demand which is significantly lower than that associated with discrete models (Poorsolhjouy P. and Misra A., 2017). In a form of GMA that leads to Cauchy-type continuum model with coupled damage and plasticity, Helmholtz free energy density and dissipation potential functions for the continuum model are obtained as the volume averages of corresponding functions defined for the grain-pair. Grain scale constitutive equations are calibrated to ensure that the model replicates the observed behavior. Since the grain-pair behavior is nonlinear, the grain-pair oriented in different directions undergo different unique loading paths as a continuum material point experiences a macro-scale loading sequence. The consequence is that the response of the granular system is highly loading-path dependent. Indeed, when a macro-scale body is subjected to a loading-path, the variously oriented grain-pair can be in different loading stages including loading, unloading, or reloading. The material response, therefore, at any stage of loading is a function of the entire loading history rather than the current loading state.

Since grain-pair interactions are key in GMA-based continuum models, the grain size effect can be incorporated by considering its influence on the grain-pair behavior. Here, we enhance the non-linear damage-plasticity grain-pair interaction previously proposed for cementitious materials by incorporating the effects of grain sizes. We introduce simple scaling relationships, based on power laws, to describe the effect of grain size on grain-pair stiffness, grain-pair damage dissipation, grain-pair branch length, and the volumetric number density of grain-pair interactions in the granular material system. Using these relationships, size-effect relationships for macroscopic response of the material (macroscopic stiffness tensor and the Cauchy stress) are predicted. These results are calculated for parameters that are calibrated using experimental data available in the literature. The predicted results show that grain-sizes can influence brittle to ductile transition and softening-hardening behavior. The results also show that macro-scale failure stress under axisymmetric loading scales with grain-sizes as has been observed from experiments on cohesive granular materials.

2. Granular Micromechanics Approach (GMA)

GMA can be categorized as a meso-scale approach that bridges the gap between continuum models and discrete models as is seen in Fig. 1. At the smallest scales, atomic models can be utilized provided the composition and initial structures are known. Indeed, provided a faithful realization of the atomic structure, these models can yield results with high degree of exactness (i.e. fidelity). For examples of their application to atomically complex materials the reader is referred to (Misra A. and Ching W.Y., 2013; Qomi M.J.A. et al., 2014). These models however are computationally costly even with the present computation and memory capacities. Moreover, they are inapplicable to large systems with complex compositions, or disordered and defective structures given the difficulties associated with the characterization and specification of such materials. In larger scales, discrete models are utilized to investigate the material behavior by simulating the interaction of macro-particles that comprise granular system (Gonzalez M. and Cuitino A.M., 2012; Hentz S. et al., 2004; Misra A. et al., 2018; Tavarez F.A. and Plesha M.E., 2007; Turco E. et al., 2019). Discrete models consist of identifying the grains in the material, their interacting neighbors, and the behavior of the interaction. For these models one needs to be able to define grains in a given volume of interest, their shapes and sizes, their contacts with their neighbor grains, their surface properties, etc. Moreover, this identification needs to be done at any loading increment, considering the fact that during loading all properties of grains and their contacts will change due to the displacement, deformation, and rearrangement of grains. If the mechano-morphology of a given granular materials can be faithfully reproduced throughout a loading process, discrete models can be used to extract high-fidelity results as depicted in Fig. 1 about the micro-level response as well as the micro-macro correlation for the material (Gonzalez M. and Cuitino A.M., 2012; Misra A. and Poorsolhjouy P., 2015b).

Fig. 1

Modeling Scales: Schematic graph showing the evolution of computational demand needed for modeling material behavior in different scales, expanding from nanometers to centimeters.

GMA incorporates data from the material microstructure and micromechanics into the continuum model in a computationally affordable statistical manner. The antecedents of the granular micromechanics approach may be traced to second quarter of the 20th century in works related to the estimation of wave velocities in granular beds in which the Hertz solution for normal contact between elastic spheres was used to find equivalent elastic moduli of regularly arranged grain packing (see (Duffy J. and Mindlin R.D., 1957; Hara G., 1935) and for a brief review (Misra A. et al., 2019)). This analysis served as the inspiration for the development of stress-strain relations for random packing of grains including certain statistical representation of the packing geometry (Chang C.S. and Misra A., 1990; Digby P.J., 1981; Misra A. and Chang C.S., 1993; Walton K., 1987). In GMA, the exact evolution of grain trajectories within the material point are not investigated. Instead, the macroscopic behavior of the granular system is derived by averaging the behavior of grain-pair interactions in different directions. In our past works, we have presented a derivation of the GMA based model applicable to cementitious granular materials in the framework of thermo-mechanics (Misra A. and Poorsolhjouy P., 2015a; Poorsolhjouy P. and Misra A., 2017). Here, this thermomechanical derivation of GMA is enhanced to account for the effect of grain-sizes. The paper is structured as follows: In section 2.1, a brief review of the general derivation of GMA within a thermo-mechanical viewpoint is presented for completeness. Section 2.2 focuses on the specifics of coupled damage-plasticity laws at micro-scale for deriving the correct macroscopic behavior of the material (for a more complete description of the micro-scale laws, the reader is referred to (Misra A. and Poorsolhjouy P., 2015a; Poorsolhjouy P. and Misra A., 2017)). In Section 2.3, the relationship between grain sizes on one hand and model variables (including branch vector, density of grain-pair contacts, as well as stiffness and damage variables) on the other, have been discussed and size-effect laws are implemented within the model. Section 3 is devoted to results of simulations for samples of various grains sizes and under different confinements. Particularly, effects of changing grain sizes on failure and its type (brittle or ductile) has been discussed. Finally, a summary and conclusion, along with an outline of continued research is presented in Section 4.

2.1 Thermo-mechanical derivation

The GMA hypothesizes that the deformation energy of a volume of granular materials can be effectively expressed in terms of the deformation energies of all its grain-pair interactions. As a consequence, the macro-scale Helmholtz free energy density, W, and dissipation potential, ψ, can be obtained as volume averages of their grain-pair counterparts, which are expressed in terms of grain-scale variables as (Misra A. and Poorsolhjouy P., 2015a; Poorsolhjouy P. and Misra A., 2017)   

$$W=\frac{1}{V}\sum _{\alpha =1}^{N_{\text{c}}}{W}^{\alpha }\left({\delta }_j^{\alpha },{\delta }_j^p,D_j^{\alpha }\right)$$(1a)

  

$$\psi =\frac{1}{V}\sum _{\alpha =1}^{N_{\text{c}}}{\psi }^{\alpha }\left({\delta }_j^{\alpha },D_j^{\alpha },{\dot{D}}_j^{\alpha },{\delta }_j^{p\alpha },{\dot{\delta }}_j^{p\alpha }\right)$$(1b)

where the summations go over all grain-pair interactions, superscript α refers to the α^th grain-pair, total number of grain-pair interactions is N_c, and the superimposed dots imply time derivative. The grain scale kinematic variables consist of the relative displacement and the plastic relative displacement between neighbor grains, ${\delta }_j^{\alpha }$ and ${\delta }_j^{p\alpha }$. Here, we note that in this model, the relative displacements between grains represents the relative displacement between the centroids of each two neighboring grains. This relative displacement can have various sources including deformation of individual grains, or relative movement between grains centroids, or deformation concentrated at the contacts, e.g. in Hertzian contact. These phenomena are not addressed separately in this model and their collective effect is lumped into the relative displacement between grain centroids. The same is true for plastic relative displacement between grain centroids. In addition, the unitless grain-scale damage parameter, ${\mathit{D}}_j^{\alpha }$, is a vector variable which represents the loss of grain-pair stiffness coefficients. In the entire document, the summation convention over repeated indices is implied, unless explicitly noted otherwise.

In this analysis, we only account for the so-called macro-displacements and do not introduce any additional kinematic descriptors or higher-gradient terms and grain-spins/rotations that are necessary for complete description of the complex granular systems (Misra A. and Poorsolhjouy P., 2016a; 2016b; Nejadsadeghi N. and Misra A., 2020; Poorsolhjouy P. and Misra A., 2019). In this case, the grain-pair relative displacement, ${\delta }_j^{\alpha }$, is related only to the first gradient of macro-displacement field. With this in mind, the macro-scale Helmholtz free energy density, W, and dissipation potential, ψ, can also be defined as functions of macroscopic variables as follows   

$$W=W\left({\varepsilon }_{ij},{\varepsilon }_{ij}^p,D_{ij}\right)$$(2a)

  

$$\psi =\psi \hspace{0.17em}\left({\varepsilon }_{ij},D_{ij},{\dot{D}}_{ij},{\varepsilon }_{ij}^p,{\dot{\varepsilon }}_{ij}^p\right)$$(2b)

where the superscript p denote plastic, ɛ_ij is the independent kinematic variable (strain tensor), and D_ij is the damage tensor which for a given direction, n_j, yields the damage vector, D_i, i.e. D_i = D_ijn_j. As standard in classical continuum mechanics, the power density of internal forces is expressed as $p^i={\sigma }_{\mathit{ij}}{\dot{u}}_{\left(\mathit{ij}\right)}={\sigma }_{\mathit{ij}}{\dot{\varepsilon }}_{\mathit{ij}}$, where σ_ij is the Cauchy stress tensor. Using the Clausius-Duhem inequality and the above definitions, the following is obtained (Poorsolhjouy P. and Misra A., 2017)

  

$$\left({\sigma }_{ij}-\frac{\partial W}{\partial {\varepsilon }_{ij}}\right){\dot{\varepsilon }}_{ij}-\left(\frac{\partial W}{\partial D_{ij}}+\frac{\partial \psi }{\partial {\dot{D}}_{ij}}\right){\dot{D}}_{ij}-\left(\frac{\partial W}{\partial {\varepsilon }_{ij}^p}+\frac{\partial \psi }{\partial {\dot{\varepsilon }}_{ij}^p}\right){\dot{\varepsilon }}_{ij}^p=0$$(3)

Since the equality in Eq. 3 should be satisfied for any arbitrary set of kinematic variables, all three terms must simultaneously vanish. For the second and third terms, since the coefficients are functions of the same kinematic variables, the weaker orthogonality condition can be sufficient (Ziegler H., 1983). As a result, the following equations are obtained

  

$${\sigma }_{ij}-\frac{\partial W}{\partial {\varepsilon }_{ij}}=0$$(4a)

  

$$\left(\frac{\partial W}{\partial D_{ij}}+\frac{\partial \psi }{\partial {\dot{D}}_{ij}}\right){\dot{D}}_{ij}=0$$(4b)

  

$$\left(\frac{\partial W}{\partial {\varepsilon }_{ij}^p}+\frac{\partial \psi }{\partial {\dot{\varepsilon }}_{ij}^p}\right){\dot{\varepsilon }}_{ij}^p=0$$(4c)

Further substituting Eq. 1a into Eq. 4a and applying chain rule the following expression for the Cauchy stress can be obtained

  

$${\sigma }_{ij}=\frac{\partial W}{\partial {\varepsilon }_{ij}}=\frac{1}{V}\sum _{\alpha =1}^{N_{\text{c}}}\frac{\partial W^{\alpha }}{\partial {\delta }_k^{\alpha }}\frac{\partial {\delta }_k^{\alpha }}{\partial {\varepsilon }_{ij}}$$(5)

In Eq. 5 the derivative of grain-pair interaction energy with respect to the displacement is defined as the conjugate force measure in the grain-scale

  

$$f_k^{\alpha }=\frac{\partial W^{\alpha }}{\partial {\delta }_k^{\alpha }}$$(6)

Assuming that the macroscopic variables including strain, ɛ_ij, plastic strain, ${\varepsilon }_{ij}^p$, and damage tensor, D_ij, are distributed linearly in the material point, the corresponding local variables defining the relative kinematics of two neighbor grains, i.e. the relative displacement, δ_i, plastic relative displacement, ${\delta }_i^p$, and the damage vector specifying the loss of stiffness between the two grains, D_i, can be derived (Misra A. and Poorsolhjouy P., 2015a; Poorsolhjouy P. and Misra A., 2017). Approximating the displacement and plastic displacement of a grain using the Taylor series expansion of the displacement and plastic displacement of its neighbor grain, allows us to define the relative displacement and relative plastic displacement between two neighbor grains (δ_i and ${\delta }_i^p$) as the product of their macroscopic counterparts (ɛ_ij and ${\varepsilon }_{ij}^p$) with the branch vector. In other words, the displacements are written as the projections of their macroscopic counterparts, in the direction of the grain-pair interaction, and then scaled by the magnitude of the branch vector. In addition, based on the definition of the macroscopic damage tensor, D_ij, the grain-scale damage vector, D_i, is given, by definition, as the product of the damage tensor and the direction of grain-pair interaction (i.e. as the projection of tensor, D_ij, in the direction of the grain-pair).   

$${\delta }_i^{\alpha }={\epsilon }_{ij}{l}_j;\mathrm{\hspace{0.17em} }{\delta }_i^{p\alpha }={\epsilon }_{ij}^p{l}_j;\mathrm{\hspace{0.17em} }{D}_i^{\alpha }=D_{ij}{n}_j$$(7)

where l_j is the branch vector joining the centroids of two neighbor grains which is given as the product of the length of the branch vector, l, and the unit vector in the direction of the contact, n_j as l_j = ln_j. Substituting Eq. 6 and 7 into Eq. 5 the expression for Cauchy stress can be rewritten as

  

$${\sigma }_{ij}=\frac{1}{V}\sum _{\alpha =1}^{N_{\text{c}}}{f}_k^{\alpha }{\delta }_{ki}{\delta }_{lj}{l}_l=\frac{1}{V}\sum _{\alpha =1}^{N_{\text{c}}}{f}_i^{\alpha }{l}_j$$(8)

It is remarked here that the widely used Eq. 8 is valid under specific assumptions as outlined in Eq. 7. Further, we observe that based on the definition of the damage vector and damage tensor (see Eq. 7) the partial derivative of the damage vector with respect to the damage tensor is given as ∂D_k/∂D_ij = n_l∂D_kl/∂D_ij = δ_ikn_j. In the same way, the partial derivative of the rate of the damage vector with respect to the rate of the damage tensor can be derived as $\partial {\dot{D}}_k/\partial {\dot{D}}_{\mathit{ij}}=n_l\partial {\dot{D}}_{\mathit{kl}}/\partial {\dot{D}}_{\mathit{ij}}={\delta }_{\mathit{ik}}{n}_j$. The same relationships can be formulated for the partial derivative of plastic displacement with respect to plastic strain as, $\partial {\delta }_k^p/\partial {\varepsilon }_{ij}^p=l_l\hspace{0.17em}\partial {\varepsilon }_{kl}^p/\partial {\varepsilon }_{ij}^p={\delta }_{ik}{l}_j$, and for their time rates, $\partial {\dot{\delta }}_k^p/\partial {\dot{\varepsilon }}_{ij}^p=l_l\hspace{0.17em}\partial {\dot{\varepsilon }}_{kl}^p/\partial {\dot{\varepsilon }}_{ij}^p={\delta }_{ik}{l}_j$. It is therefore derived that $\partial D_k^{\alpha }/\partial D_{ij}=\partial {\dot{D}}_k^{\alpha }/\partial {\dot{D}}_{ij}$ and $\partial {\dot{\delta }}_k^{p\alpha }/\partial {\dot{\varepsilon }}_{ij}^p=\hspace{0.17em}\partial {\delta }_k^{p\alpha }/\partial {\varepsilon }_{ij}^p$. Substituting this assumption, as well as Eqs. 1a and 1b into Eqs. 4b and 4c, results in

  

$$\sum _{\alpha =1}^{N_{\text{c}}}\left(\left(\frac{\partial W^{\alpha }}{\partial D_i^{\alpha }}+\frac{\partial {\psi }^{\alpha }}{\partial {\dot{D}}_i^{\alpha }}\right){\dot{D}}_i^{\alpha }\right)=0$$(9a)

  

$$\sum _{\alpha =1}^{N_{\text{c}}}\left(\left(\frac{\partial W^{\alpha }}{\partial {\delta }_i^{p\alpha }}+\frac{\partial {\psi }^{\alpha }}{\partial {\dot{\delta }}_i^{p\alpha }}\right){\dot{\delta }}_i^{p\alpha }\right)=0$$(9b)

Now it should be noted that the summations in Eq. 9 should hold for any number of grain-pair interactions and thus, the equality should be satisfied in a term-by-term manner.

  

$$\left(\frac{\partial W^{\alpha }}{\partial D_i^{\alpha }}+\frac{\partial {\psi }^{\alpha }}{\partial {\dot{D}}_i^{\alpha }}\right){\dot{D}}_i^{\alpha }=0$$(10a)

  

$$\left(\frac{\partial W^{\alpha }}{\partial {\delta }_i^{\alpha }}+\frac{\partial {\psi }^{\alpha }}{\partial {\dot{\delta }}_i^{p\alpha }}\right){\dot{\delta }}_i^{p\alpha }=0$$(10b)

Combining Eq. 6 and 10 results in   

$$\left(f_j^{\alpha }-\frac{\partial W^{\alpha }}{\partial {\delta }_j^{\alpha }}\right){\dot{\delta }}_j^{\alpha }-\left(\frac{\partial W^{\alpha }}{\partial D_j^{\alpha }}+\frac{\partial {\psi }^{\alpha }}{\partial {\dot{D}}_j^{\alpha }}\right){\dot{D}}_j^{\alpha }-\left(\frac{\partial W^{\alpha }}{\partial {\delta }_j^{\alpha }}+\frac{\partial {\psi }^{\alpha }}{\partial {\dot{\delta }}_j^{p\alpha }}\right){\dot{\delta }}_j^{p\alpha }=0$$(11)

which leads to the following micro-scale Clausius-Duhem type inequality for the α^th inter-granular interaction:   

$$f_j^{\alpha }{\dot{\delta }}_j^{\alpha }-{\dot{W}}^{\alpha }=d^{\alpha }\ge 0$$(12)

where the grain-scale dissipation, d^α, is defined as   

$$d^{\alpha }=\frac{\partial {\psi }^{\alpha }}{\partial {\dot{D}}_j^{\alpha }}{\dot{D}}_j^{\alpha }+\frac{\partial {\psi }^{\alpha }}{\partial {\dot{\delta }}_j^{p\alpha }}{\dot{\delta }}_j^{p\alpha }\ge 0$$(13)

and the time derivative of micro-scale free energy, W^α, is

  

$${\dot{W}}^{\alpha }=\frac{\partial W^{\alpha }}{\partial {\delta }_j^{\alpha }}{\dot{\delta }}_j^{\alpha }+\frac{\partial W^{\alpha }}{\partial D_j^{\alpha }}{\dot{D}}_j^{\alpha }+\frac{\partial W^{\alpha }}{\partial {\delta }_j^{p\alpha }}{\dot{\delta }}_j^{p\alpha }$$(14)

Thus, employing appropriate formulation for the Helmholtz energy, W^α, and dissipation potential, ψ^α, we can completely describe the grain-pair force-displacement relationships (using Eq. 12) and in turn, the classical stress-strain behavior of a granular system (using Eq. 8).

2.2 Grain-scale coupled damage-plasticity relationships

At this juncture, it is useful to formulate the grain-pair energy and dissipation functions in terms of grain-pair displacement decomposed into two components, one along the vector connecting the two grain-centroids (branch vector), termed as normal component, and the other in the orthogonal direction, termed as the tangential component (as depicted in the inset in Fig. 2). Accordingly, a local Cartesian coordinate system, nst, is defined composed of three unit vectors: unit normal vector n_i in the direction of branch vector, l_i, and two orthogonal vectors lying in the tangential plane denoted as s_i and t_i. The direction cosines of these local coordinate axes are given as   

$$\begin{array}{l}{n}_i=⟨\text{cos\hspace{0.17em}}\theta ,\text{sin\hspace{0.17em}}\theta \hspace{0.17em}\text{cos\hspace{0.17em}}\phi ,\text{sin\hspace{0.17em}}\theta \hspace{0.17em}\text{sin\hspace{0.17em}}\phi ⟩\\ s_i=⟨-\text{sin\hspace{0.17em}}\theta ,\text{cos\hspace{0.17em}}\theta \hspace{0.17em}\text{cos\hspace{0.17em}}\phi ,\text{cos\hspace{0.17em}}\theta \hspace{0.17em}\text{sin\hspace{0.17em}}\phi ⟩\\ t_i=⟨0,-\text{sin\hspace{0.17em}}\phi ,\text{cos\hspace{0.17em}}\phi ⟩\end{array}$$(15)

using spherical coordinates (See Fig. 2). The normal and tangential components of a grain-pair are then given as   

$$\begin{array}{l}{\delta }_{\text{n}}={\delta }_i{n}_i\hfill \\ {\delta }_{\text{w}}=\sqrt{{({\delta }_i{s}_i)}^2+{({\delta }_i{t}_i)}^2}\hfill \end{array}\};\hspace{0.17em}\text{where\hspace{0.17em}}{\delta }_i={\varepsilon }_{ij}{l}_j$$(16)

Fig. 2

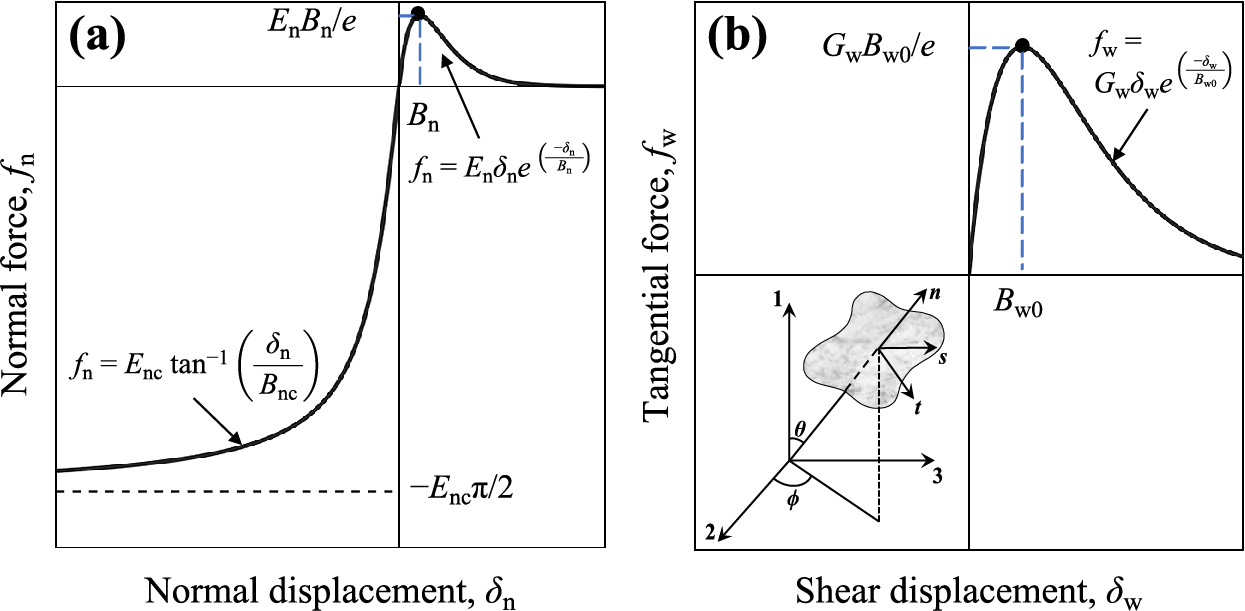
Intergranular Force-Laws: (a) Grain-pair force-displacement curve in normal direction showing the tension-compression asymmetry typical of cohesive grain interactions. (b) Grain-pair force-displacement curve in the tangential direction and inset schematic of an interface between two grains and the global and local coordinate axes. Damage and stiffness parameters defining the grain-pair interactions are displayed on the graphs.

It should be noted that the subscripts n and w, refer to normal and tangential components and they do not represent vector quantities. Summation convention, therefore, does not apply to them. The grain free energy and dissipation potential are written as the summations of their normal and tangential components, $W^{\alpha }=W_{\text{n}}^{\alpha }+W_{\text{w}}^{\alpha }$ and ${\psi }^{\alpha }={\psi }_{\text{n}}^{\alpha }+{\psi }_{\text{w}}^{\alpha }$. To account for damage and plasticity, the normal and tangential components of inter-granular free energy take the following form (Misra A. and Poorsolhjouy P., 2015a; Poorsolhjouy P. and Misra A., 2017)

  

$$\begin{array}{l}{W}_{\text{n}}^{\alpha }=\frac{1}{2}{E}_{\text{n}}^{\alpha }(1-D_{\text{n}}^{\alpha }){({\delta }_{\text{n}}^{\alpha })}^2-h_{\text{n}}^{\alpha }{\delta }_{\text{n}}^{p\alpha }\\ W_{\text{w}}^{\alpha }=\frac{1}{2}{G}_{\text{w}}^{\alpha }(1-D_{\text{w}}^{\alpha }){({\delta }_{\text{w}}^{\alpha })}^2-h_{\text{w}}^{\alpha }{\delta }_{\text{w}}^{p\alpha }\end{array}$$(17)

Where $E_{\text{n}}^{\alpha }$ and $G_{\text{w}}^{\alpha }$ are the grain-pair elastic stiffness, $h_{\text{n}}^{\alpha }$ and $h_{\text{w}}^{\alpha }$ are the grain-pair generalized forces, and ${\delta }_{\text{n}}^{p\alpha }$ and ${\delta }_{\text{w}}^{p\alpha }$ are the grain-pair plastic displacements in normal and tangential directions, respectively. Normal and tangential components of inter-granular dissipation potential are represented by the sum of the dissipations due to damage and plasticity   

$$\begin{array}{l}{\psi }_{\text{n}}^{\alpha }=Y_{\text{n}}^{\alpha }\left|{\dot{D}}_{\text{n}}^{\alpha }\right|+Z_{\text{n}}^{\alpha }\left|{\dot{\delta }}_{\text{n}}^{p\alpha }\right|\ge 0\\ {\psi }_{\text{w}}^{\alpha }=Y_{\text{w}}^{\alpha }\left|{\dot{D}}_{\text{w}}^{\alpha }\right|+Z_{\text{w}}^{\alpha }\left|{\dot{\delta }}_{\text{w}}^{p\alpha }\right|\ge 0\end{array}$$(18)

where dissipation coefficients Y and Z denote generalized forces that are conjugates of the inter-granular damage and plastic dissipation, respectively. The forms assumed in Eqs. 17 and 18 result in rate-independent form of damage and plasticity as opposed to rate-dependent form that are also relevant to certain granular systems (Giorgio I. and Scerrato D., 2017; Misra A. and Singh V., 2014a; 2014b). Substituting Eqs. 17 and 18 into Eqs. 10a and 10b rewritten for normal and tangential directions one can find the dissipation coefficients, Y and Z, duals of inter-granular damage and plastic displacements respectively.

  

$$Y_{\text{n}}^{\alpha }=\frac{1}{2}{E}_{\text{n}}^{\alpha }\hspace{0.17em}{\left({\delta }_{\text{n}}^{\alpha }\right)}^2\hspace{0.17em}\text{sign\hspace{0.17em}}\left({\dot{D}}_{\text{n}}^{\alpha }\right);\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{Y}_{\text{w}}^{\alpha }=\frac{1}{2}{G}_{\text{w}}^{\alpha }{\left({\delta }_{\text{w}}^{\alpha }\right)}^2\hspace{0.17em}\text{sign\hspace{0.17em}}\left({\dot{D}}_{\text{w}}^{\alpha }\right)$$(19a)

  

$$Z_{\text{n}}^{\alpha }=h_{\text{n}}^{\alpha }\text{sign\hspace{0.17em}}\left({\dot{\delta }}_{\text{n}}^{p\alpha }\right);\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }{Z}_{\text{w}}^{\alpha }=h_{\text{w}}^{\alpha }\text{sign\hspace{0.17em}}\left({\dot{\delta }}_{\text{w}}^{p\alpha }\right)$$(19b)

Further, normal and tangential components of grain-pair force vector can be found by substituting Eq. 17 into Eq. 7

  

$$\begin{array}{l}{f}_{\text{n}}^{\alpha }=\frac{\partial W^{\alpha }}{\partial {\delta }_{\text{n}}^{\alpha }}=k_{\text{n}}^{\alpha }{\delta }_{\text{n}}^{\alpha }=E_{\text{n}}^{\alpha }\hspace{0.17em}\left(1-D_{\text{n}}^{\alpha }\right)\hspace{0.17em}{\delta }_{\text{n}}^{\alpha }\\ f_{\text{w}}^{\alpha }=\frac{\partial W^{\alpha }}{\partial {\delta }_{\text{w}}^{\alpha }}=k_{\text{w}}^{\alpha }{\delta }_{\text{w}}^{\alpha }=G_{\text{w}}^{\alpha }\hspace{0.17em}\left(1-D_{\text{w}}^{\alpha }\right)\hspace{0.17em}{\delta }_{\text{w}}^{\alpha }\end{array}$$(20)

The details of particular forms of the damage functions D_n and D_w and related parameters that are applicable to cohesive granular materials have been described in details in our previous work and is therefore not repeated here (Poorsolhjouy P. and Misra A., 2017). Fig. 2 contains the force-displacement relationships, as well as schematic curves of the functional forms of the force-laws. Moreover, a selection of the major parameters used in the relationships and their role in the force-displacement curves are depicted in the Fig. 2. The tension-compression asymmetry of grain-pair behavior and the post peak softening due to damage under grain-pair tension and shear is clearly illustrated. The grain-pair tension-compression asymmetry is significant in induced anisotropy evolution in granular systems (Jia H. et al., 2017). Table 1 lists all the model parameters and their numerical values used in this study. For more details and implementation of loading-unloading-reloading criteria, ratio between failure force in normal compression to that in normal tension (captured in parameter R), effect of grain-scale relative normal displacement on the grain-scale damage parameter in shear direction (captured in parameters α₁, α₂, and α₃), the effect of confinement on the compressive behavior of grain-pair interactions (captured in the parameter α₄), as well as the incorporation of permanent deformation in grain-pair interactions (captured in parameters β_n and β_w), the reader is referred to (Misra A. and Poorsolhjouy P., 2015a; Poorsolhjouy P. and Misra A., 2017).

Table 1 Model parameters used in this study.

Model Parameters	Value
$E_{\text{no}}^T$	3.5 kN/m
R	17.5
Gw	1 kN/m
Bn	7E–10 m
Bnc	3E–9 m
Bwo	1.5E–9 m
α1	10.5
α2	7
α3	0.01
α4	0.05 MPa−1
βn	0.0
βw	0.6
l0	10E–6 m
ρc	1E18 mm−3

Substituting Eqs. 7 and 20 into the equation for Cauchy stress (Eq. 8) and taking the strain tensor out of the summation, the equation for the fourth rank stiffness tensor can be derived as   

$$C_{ijkl}=\frac{1}{V}\sum _{\alpha =1}^{N_{\text{c}}}{k}_{ik}{l}_j{l}_l$$(21)

where N_c is the total number of grain-pair interactions within the material point. Total number of grain-pair interactions can be calculated as half of the product of the total number of grains, N, and the mean coordination number, z. Using two new parameters, namely the volumetric number density of grain-pair interactions ρ^c = N_c/V and the directional density distribution of grain-pair contacts, ξ(θ,φ), this summation over all contacts can be transformed into an integration over all different orientations as   

$$C_{ijkl}=l^2{\rho }^c\underset{\theta =0}{\overset{\pi }{\int }}\underset{\phi =0}{\overset{2\pi }{\int }}\left(k_{ik}{n}_j{n}_l\right)\xi (\theta ,\phi )\text{sin\hspace{0.17em}}\theta \text{d}\theta \text{d}\phi$$(22)

where l is the average value of grain-pair branch length in the whole RVE. Using the same approach, the Cauchy stress will also be derived in the integral form as

  

$${\sigma }_{ij}=l{\rho }^c\underset{\theta =0}{\overset{\pi }{\int }}\underset{\phi =0}{\overset{2\pi }{\int }}\left(f_i{n}_j\right)\xi \hspace{0.17em}\text{sin\hspace{0.17em}}\theta \text{d}\theta \text{d}\phi$$(23)

For more detailed description of the procedure used to transform the summations into integration see (Misra A. and Poorsolhjouy P., 2016c).

2.3 Scaling laws for grain-size effect

Let us consider two different granular materials whose average grain sizes are d₁ and d₂, where without loss on generality say d₁ < d₂, and the subscripts refer to the material type 1 and type 2. A set of size scaling relationships are hypothesized, inspired by the principles of renormalization, to compare the two materials based upon physical arguments. For example, it is reasonable to expect that the average grain-pair branch length of material 2 is related to that of the material 1, through the following simple scaling (in the subsequent equations (Eqs. 24–28) the subscripts 1 and 2 will refer to the two granular materials and are not tensor quantities)

  

$$l_2=l_1\left(\frac{d_2}{d_1}\right)$$(24)

Similarly, the volumetric number density of grain-pair interactions, ρ^c, of the two types of granular materials can be related to each other through the following scaling relationship

  

$${{\rho }^{\text{c}}}_2={{\rho }^{\text{c}}}_1{\left(\frac{d_2}{d_1}\right)}^{\alpha }$$(25)

Where the exponent, α, can vary widely depending not only upon the average grain sizes but also the grain size distributions as well as the packing density. The exponent, α, will also depend upon the problem dimension (that is whether the granular material is a packing of 2D grains or 3D grains) and the grain geometry. For the ideal case of 3D packings of monodisperse spherical particles in a regular closed-pack assembly, the exponent, α, will reach the lower bound of −3 (negative 3). It is evident that the value of the exponent α should be negative since the volumetric number density of grain-pair interactions is inversely related to grain size. Calibrating the value will be complicated for random packings of cohesive particles with irregular geometries and complex particle size distributions. However, the exponent will be bound within the bound −3 < α < 0.

Further, the deformation behavior of grain-pair depends not only upon the grain-shape, its surface characteristics as well as the cohesive mechanisms, but also on the size of the grain. While the grain size dependence of grain-pair stiffness is complex, the following size scaling is expected even for grains of similar composition and shapes   

$${(E_{\text{n}})}_2={(E_{\text{n}})}_1{\left(\frac{d_2}{d_1}\right)}^{\beta }\hspace{0.17em}\text{and\hspace{0.17em}}{(G_{\text{w}})}_2={(G_{\text{w}})}_1{\left(\frac{d_2}{d_1}\right)}^{\beta }$$(26)

where parameter β determines the relative scaling of grain-pair initial (unloaded) stiffness coefficients depending on grain-size. Considering size-effect laws discussed in the literature (Cordero N.M. et al., 2010; 2012; Fredrich J.T. et al., 1990), the numerical value of parameter β is expected to be negative, that is the larger grains result in less stiff grain-pair in comparison to smaller grains.

In addition, the complete force-displacement behavior of a grain pair, particularly its failure behavior, will also be scaled with the change of grain size. The following scaling relationships are introduced for those model parameters that describe the relative displacement where the grain-pair forces reach their peak

  

$$\begin{array}{l}{(B_{\text{n}})}_2={(B_{\text{n}})}_1{\left(\frac{d_2}{d_1}\right)}^{\gamma };\mathrm{\hspace{0.17em} }{(B_{\text{nc}})}_2={(B_{\text{nc}})}_1{\left(\frac{d_2}{d_1}\right)}^{\gamma };\\ {(B_{\text{wo}})}_2={(B_{\text{wo}})}_1{\left(\frac{d_2}{d_1}\right)}^{\gamma };\end{array}$$(27)

Based on experimental results in the literature, it is evident that coarser grains show a more ductile behavior, which means they can store more energy. As a result, the damage parameter used in our model (in normal tension B_n, in normal compression, B_nc, and in tangential direction, B_wo) should be proportional to the grain size. That is, aggregates of larger sizes will fail at a larger displacement. This implies that the size-effect parameter should have a positive value, γ > 0.

Fig. 3 presents an illustrative parametric study to demonstrate how the size-effect parameters influence the grain-pair behavior. The schematic curves in Fig. 3 present force-displacement relationships for normal interaction of grain-pairs, under tension, for varying grain-sizes and for varying size-effect parameters. The effect of the size-effect laws on tangential interaction as well as the normal compressive interactions is similar and not presented here for brevity. It is seen in Fig. 3a that negative β values lead to stiffer behavior for smaller grains. It is also seen that by keeping β constant and increasing γ, smaller grains show smaller energy storage capacities and smaller failure stress. Inversely, keeping β constant and increasing γ results in larger grains showing a more ductile behavior.

Fig. 3

Parametric Studies: Investigating the effects of size-effect parameters on the behavior of contacts in normal tension. Force-displacement curves for constant grain size and varying model parameters (a) and force-displacement curves for varying grain sizes with constant model parameters, (a). Model parameters used in (b), β = −1 and γ = 1, are those used in the analysis. Normal interactions in tension are chosen as examples to show the effects of size effect parameters on stiffness and damage.

It is also observed (from both Figs. 3a and 3b) that for positive values of γ, if γ = −β, smaller grains show larger stiffness, however, they fail at the same force value and smaller displacement values compared to larger grains. Accordingly, larger grains have a more ductile behavior and a larger work of failure (more energy storage capacity) which is in agreement with typical empirical observations reported in the literature.

It is noted that here that the choice of parameter set for simulating the behavior of the specific material investigated in this paper, was done by considering the macroscopic behavior of the material. At the macroscopic level, combining (i) Eq. 20, which describes the mathematical form of the grain-pair stiffness coefficients as function of the stiffness and damage parameters, (ii) Eq. 24, which describes the effect of grain sizes on the magnitude of the branch vector, and (iii) Eq. 26, which describes the effect of grain sizes on the volumetric number density of grain-pair interactions and substituting them into Eq. 22 which derives the macroscopic stiffness tensor, we can derive the ratio between initial macroscopic stiffness tensor of a material with grain size of d₂ to that of a material with grain size of d₁ as follows   

$$\begin{array}{l}\frac{{\left(C_{ijkl}\right)}_2}{{\left(C_{ijkl}\right)}_1}=\frac{{\left(l_2\right)}^2{\rho }_2^{\text{c}}{\left(\underset{\theta =0}{\overset{\pi }{\int }}\underset{\phi =0}{\overset{2\pi }{\int }}\left(k_{ik}{n}_j{n}_l\right)\xi (\theta ,\phi )\hspace{0.17em}\text{sin\hspace{0.17em}}\theta \text{d}\theta \text{d}\phi \right)}_2}{{\left(l_1\right)}^2{\rho }_1^{\text{c}}{\left(\underset{\theta =0}{\overset{\pi }{\int }}\underset{\phi =0}{\overset{2\pi }{\int }}\left(k_{ik}{n}_j{n}_l\right)\xi (\theta ,\phi )\hspace{0.17em}\text{sin\hspace{0.17em}}\theta \text{d}\theta \text{d}\phi \right)}_1}\\ ={\left(\frac{d_2}{d_1}\right)}^2\hspace{0.17em}{\left(\frac{d_2}{d_1}\right)}^{\alpha }\hspace{0.17em}{\left(\frac{d_2}{d_1}\right)}^{\beta }\end{array}$$(28)

since the magnitude of the branch vector, l, is scaled linearly with size, volumetric number density of grain-pair interactions, ρ^c, scales with grain size through exponent α, and the initial stiffness coefficient of interacting grains at the unloaded state is scaled by β. Accordingly, the initial macroscopic stiffness tensor of a material with grain size d₂ can be derived as a function of the stiffness tensor of the material with grain size of d₁ as follows

  

$${\left(C_{ijkl}\right)}_2={\left(C_{ijkl}\right)}_1{\left(\frac{d_2}{d_1}\right)}^{2+\alpha +\beta }$$(29)

It should be noted that this simple close-form solution is only available for the components of stiffness tensor at the initial (virgin) state. Once the material is subjected to loading, every grain-pair will experience a unique history of relative displacements according to its direction and therefore its force-displacement relationship will be scaled in a nonlinear manner dictated by Eq. 27. As a result, the macroscopic behavior, represented by the evolution of macroscopic tangent stiffness tensor, will be scaled by grain size in a nonlinear fashion which depends on the loading path. In what follows, numerical results of the effects of changing grain size on the stress-strain behavior of a specific granular material is presented to demonstrate the effectiveness of the model and the scaling laws presented.

3. Results

Inspired by the experimental results presented in (Fredrich J.T. et al., 1990), the enhanced GMA based model described in section 2 was applied to simulate the conventional triaxial behavior of cohesive granular materials for a range of grain sizes. The nominal grain sizes of for these simulations ranged from 0.02 m to 0.00001 m. Furthermore, the confining pressure for these conventional triaxial simulations ranged from 0.0 MPa to 400.0 MPa. In these simulations, the parameter values used in our previous work on cohesive granular materials (Misra A. and Poorsolhjouy P., 2015a; Poorsolhjouy P. and Misra A., 2017) are used (See Table 1).

Calibration of size-effect parameters was done by investigating their combined effect on the grain-scale behavior as well as the macroscopic continuum level behavior. By considering the physical meaning of each of the exponents, as it was already discussed in Section 2.3, it is clear that α < 0, β < 0, and γ > 0. However, the choice of the exact value of the parameters is done based upon their combined effect in the overall behavior of the material and by mimicking experimental results. In this paper, we calibrate model parameters based on the experimental results presented in (Fredrich J.T. et al., 1990). We first observe that, for the material under consideration, the initial stiffness coefficients are inversely related to grain-sizes. Considering this and using Eq. 29, it is clear that for this material we need to confine the size-effect parameters such that 2 + α + β < 0. However, it is also seen in (Fredrich J.T. et al., 1990) that this inverse relationship is not very strong and therefore, |2 + α + β| should be a small number.

Once these the limits stated above are set, the calibration of the exact values of the parameters, is done by comparing the model results to the stress-strain curves for conventional triaxial test under different confining pressures for materials with different grain sizes. Just like in the grain-scale (as shown in the parametric studies in Fig. 3), the effect of size-effect parameters on the macroscopic behavior of the material is also complicated. Accordingly, the choice of the parameters used in this study and for the material under consideration (presented in Table 2) is done for deriving an overall fit between the results. A detailed investigation of the influence of the various parameters remains a topic for further research and investigation.

Table 2 Size effect parameters.

Size effect Parameters	Value (unitless)
α	−1.2
β	−1.0
γ	1.0

The simulated conventional triaxial compressive experiments are typically performed in two, sequential phases. In the first phase, termed as the confinement phase, the material specimen is subjected to an incrementally increasing hydrostatic confinement to the desired confining pressure, such that (σ₁₁ = σ₂₂ = σ₃₃ = σ_conf). In the second phase, the material specimen is subjected to deviatoric loading by incrementally increasing the stress in the vertical direction. In this deviatoric phase, the vertical strain, ɛ₁₁, is increased while the two horizontal stresses (σ₂₂ and σ₃₃) are kept constant.

It is well known for cohesive granular materials that increasing confinement results in increasing the material tangential stiffness as well as the failure stress under triaxial loading. The simulations described in this paper, show that reducing grain-size can also result in increasing stiffness and failure stress. For a clear visualization, the results of the triaxial compression simulations are categorized into two cases: Case 1 for small confinements (0.0, 5.0, and 20 MPa), and Case 2 for large confinements (50, 100, 200, and 400 MPa). This distinction has been made to highlight the significant change in the nature of stress-strain relationship as the confinement becomes larger than a value lying between 20 and 50 MPa. The different natures of the stress-strain relationship are clear from the plots given in Figs. 4 and 5 for the two cases. In Fig. 4, we give the evolution of the deviatoric stress, q = σ₁₁ −σ_conf, as the applied vertical strain, ɛ₁₁, is increased for granular materials of different grain sizes for the case of small confinements (< 20 MPa). Further, in Fig. 5, we show the same set of results for granular materials of different grain sizes for the case of large confinement (> 50 MPa). It is clear from Figs. 4 and 5, that both the stiffness and strength increase as the grain-sizes decrease. Moreover, this stiffening and strengthening effects are greater at the higher levels of confinements as seen from Fig. 5.

Fig. 4

Stress-Strain in Small Confinement: Evolution of the deviatoric stress, q = σ₁₁ − σ₂₂, during triaxial loading (application of ɛ₁₁) for initial confining pressures of 0.0, 5.0, and 20.0 MPa for all different grain sizes.

Fig. 5

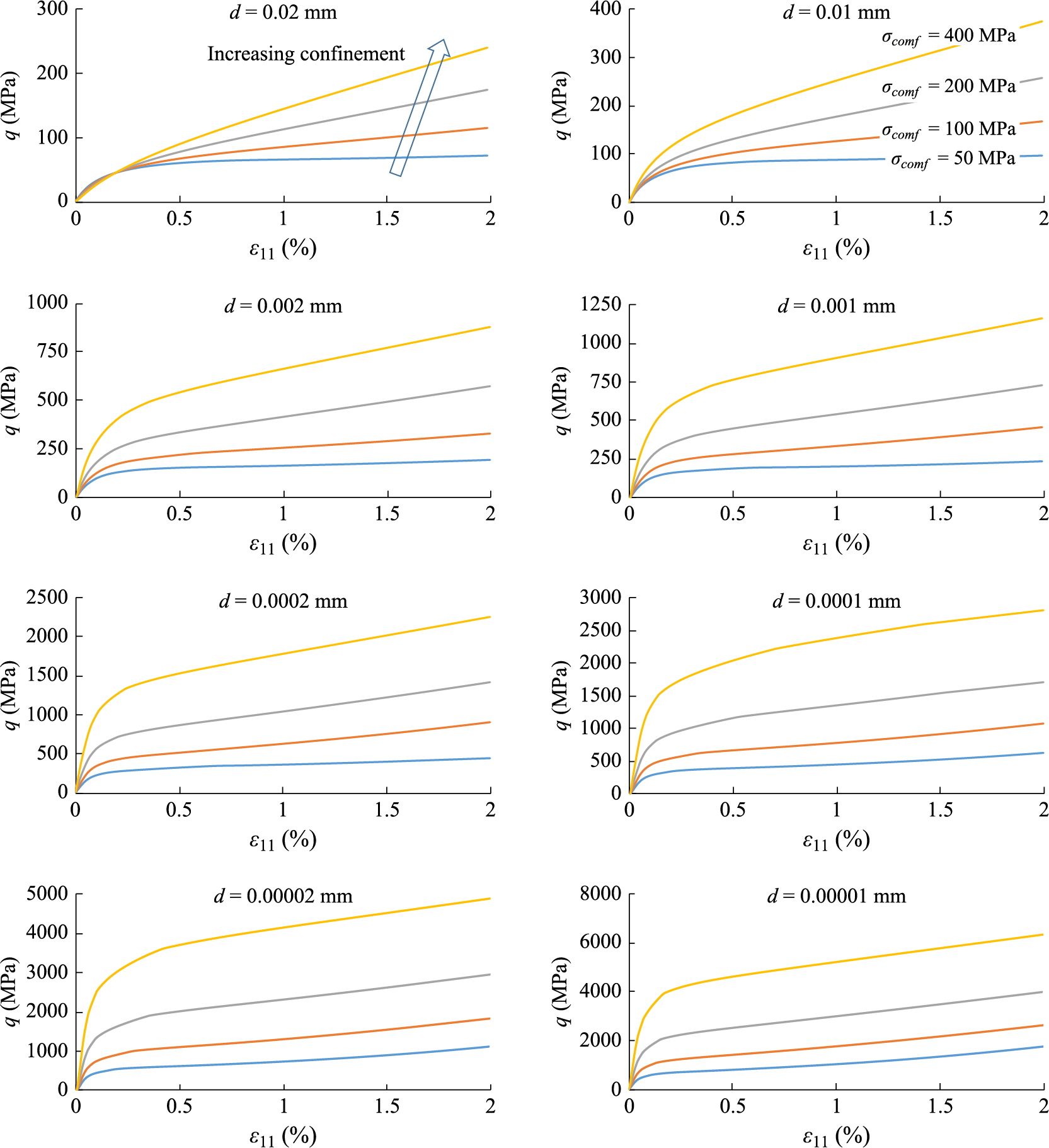
Stress-Strain in Large Confinement: Evolution of the deviatoric stress, q = σ₁₁ − σ₂₂, during triaxial loading (application of ɛ₁₁) for initial confining pressures of 50, 100, 200, and 400 MPa for all different grain sizes.

More importantly, the results in Figs. 4 and 5 illustrate the transition in the nature of stress-strain behavior from “brittle failure” to “ductile failure”. The observation that failure behavior transforms from brittle to ductile with increasing confinement is well-known from experiments (Bažant Z.P. et al., 1996; Mahboubi A. and Ajorloo A., 2005; Sfer D. et al., 2002) as well as from simulations using GMA that support the experimental results (Misra A. and Poorsolhjouy P., 2015a). A clear peak in the stress-strain relationship, defined by the point at which the stiffness (slope of the stress-strain curve) reaches zero, characterizes brittle failure. On the other hand, the lack of a peak but a clear change in slope of the stress-strain curve characterizes a ductile failure. Granular materials showing ductile response have a yield point (defined here as the stress and strain point at which there is a significant reduction in stiffness), followed by ideal plastic behavior or a hardening-type behavior.

As expected for a given grain size and changing confinement, the simulation results presented in Figs. 4 and 5 confirm the above observations. It is noteworthy, however, that the transition from brittle to ductile failure can also be affected by decreasing the grain size for a given confinement as explicated in both Figs. 4 and 5. Indeed, if we examine the behavior for different grain sizes at 20 MPa confinement given in Fig. 4, we can observe that for grain sizes d > 0.0001 mm, there is a clear peak in the stress-strain curves which implies a brittle failure. We note that in this context, the term “brittle failure” signifies a loss of ability of the material to support additional stress. The described “brittle failure” is distinct from the term “brittle behavior”, which, as opposed to “ductile behavior”, implies a low capacity to store energy (i.e. a low work of failure). In contrast, for the same confinement (20 MPa), a “ductile failure” can be observed in Fig. 5 characterized by a yield point followed by strain-hardening for the material. The transition between brittle and ductile failure happens for material with smaller grain sizes of d ≤ 0.0001 at a confining pressures between 5 MPa and 20 MPa (see Fig. 4 for d = 0.0001, 0.00002 mm and 0.00001 mm). For larger grains, this transition is observed at confinement between 20 MPa and 50 MPa as seen from comparison of results in Figs. 4 and 5. This transition from brittle to “ductile failure” is also observed experimentally as seen in (Fredrich J.T. et al., 1990).

The above observation can be further elucidated by investigating the evolution of failure stresses and yield stresses with the grain-sizes. For the case of small confinements, we can identify a failure point as the peak of the stress-strain curve. Fig. 6a gives a plot of the failure deviatoric stress versus grain sizes for small confinements. On the other hand, for large confinements, it is possible to identify a yield deviatoric stress as the point of rapid slope change of the stress-strain curve. In Fig. 6b, the yield deviatoric stress is plotted against grain sizes for large confinements.

Fig. 6

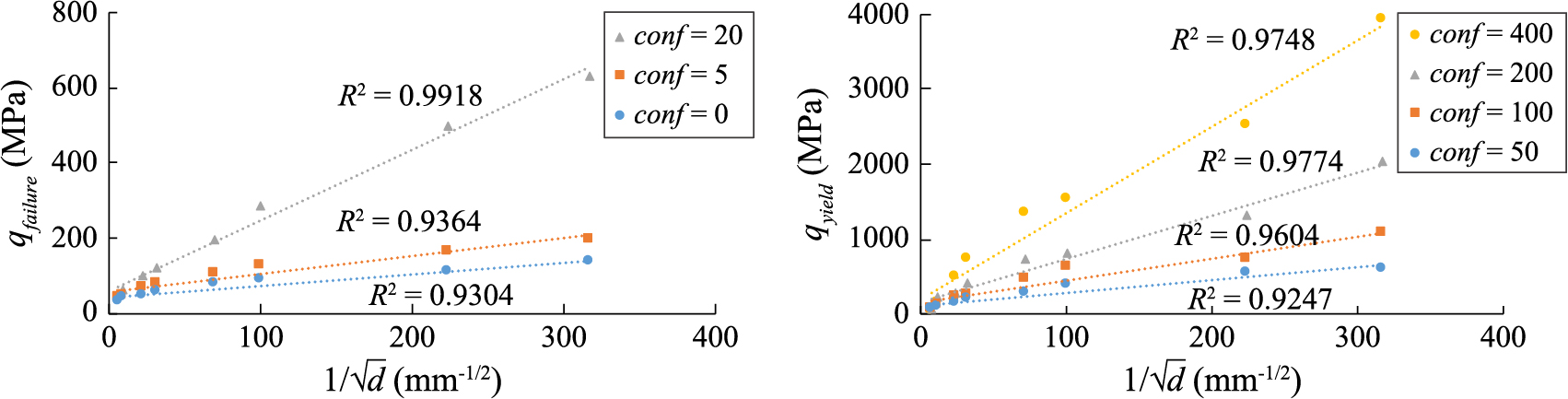
Failure/Yield Stress vs. Size: Change of failure stress for lowly confined cases, σ_conf ≤ 20 MPa, and yield stress for highly confined cases, σ_conf > 20 MPa by change of grain size.

For both the failure and yield stress we see a clear trend of inverse relationship with grain sizes from Figs. 6a and 6b. Interestingly, both failure stress and yield stress increase proportionally with increasing $1/\sqrt{d}$ as a good approximation (note the values of R-squared in the graphs). It is remarkable that the same linear patterns describing the dependency of the failure and yield values on $1/\sqrt{d}$ has been observed experimentally for granular geomaterials (Fredrich J.T. et al., 1990). The inverse relationship of yield stress with grain-size have been shown through finite element modeling using generalized continuum models (Cordero N.M. et al., 2012) as well as experiments (Jia D. et al., 2003).

Finally, it is interesting to investigate the effect of grain-sizes on the evolution of lateral deformations during triaxial tests. In Fig. 7, the evolution of volumetric strain (ɛ_v = ɛ_ii = ɛ₁₁ + ɛ₂₂ + ɛ₃₃) is plotted against the applied vertical strain, ɛ₁₁, during the deviatoric phase. In these plots, the compressive volumetric stress is shown as positive as is standard in granular mechanics. These results show that increasing grain size (as well as increasing confinement) result in a transition from dilation to compaction during triaxial testing. Triaxial tests with low confinement experience compaction (compressive volume strain) over a small interval of axial strain before transitioning to dilation (tensile volume strain). For larger confinement, however, the volumetric strain evolution tends towards compressive region. In fact, for very large confinement, no dilation is observed and the volume monotonically decreases as the loading progresses.

Fig. 7

Volumetric Strain Behavior: Evolution of volumetric strain during deviatoric loading for all different sizes and different initial confinements (0, 5, 20, 50, 100, 200, and 400 MPa). Curves for higher confinements (50 MPa to 400 MPa are too close to distinguish). Note that in these plots compression is taken as positive.

More importantly, these results show the clear effect of grain sizes on the volumetric strain evolution. As grain sizes decrease, the volumetric strain evolves increasingly to the tensile region. Indeed for the smallest grain size (d = 0.00001 mm) used in the simulations, the volumetric strain if found to be tensile for all the simulated confinement levels. These results predict that granular materials composed of small grains tend to be more dilative than those composed of large grains. Moreover, the dilative behavior of small-grained materials appears to have limited effect of confinement (particularly for the granular system simulated in this work). We note that in the present study, the focus upon dense cohesive granular materials such as rocks, concrete, and other cementitious materials, in which the effect of initial density variation on the volumetric strain is typically limited. It is noteworthy though that in the present model the effect of initial porosity is incorporated within the parameters of grain-pair interactions. Here, we have evaluated the effect of confining stress on volumetric strain for different grain sizes as shown in Fig. 7. The effect of initial porosity can also be evaluated for similar materials with varying initial porosities.

4. Summary and conclusions

The described work represents an effort to systematically investigate the influences that grain-sizes have upon the macro-scale or collective response of granular systems with very large number (> 10⁶) of grains. It was shown that the GMA based model for damage and plasticity of cohesive granular materials, which was previously derived and validated by the authors, can be enhanced to incorporate the effects of grain size. To this end, a micromechanical viewpoint is utilized to implement the grain-size effect. The set of scaling laws was incorporated into the GMA based model. These include scaling laws for: volume density of grain-pair interactions, grain-pair branch lengths, grain-pair elastic stiffness in normal and tangential directions, and the grain-pair damage parameters in normal and tangential directions. In the presented modeling approach, these microscopic (grain-scale) scaling laws are found to profoundly influence the macro-scale stress-strain response of a granular system.

The derived model is applied to simulate triaxial compressive tests for cohesive granular materials for a range of grain sizes and confinements. The simulation results demonstrate that reduction in grain size results in a stiffer stress-strain behavior, a transition from brittle to ductile type of failure characterized by peak or yield points in the stress-strain curves, and an increase in the failure and yield stresses. These effects, in some ways, mirror the behavior of granular materials for a given grain-size with change in confinement. It is remarkable, therefore, that change of grain-sizes show similar variation in the material macro-scale behavior. Furthermore, the volumetric behavior of the samples are also seen to depend, in addition to the amount of initial confinement, on the grain sizes. Samples of smaller grain sizes demonstrate more tendency towards dilation (tensile volume strain) compared to samples of larger grain sizes. At very small grain sizes, no amount of compaction is sufficient to keep the volumetric strain in compressive domain. Future work will consider further details of the effect of grain-size on deformation and failure mechanism of granular system, including the formation of shear, compression-tension or mixed-model localization bands and their orientation with respect to the loading directions.

Acknowledgements

This research is supported in part by the United States National Science Foundation grant CMMI-1068528 and CMMI-1727433

References

•  Bažant  Z.P.,  Xiang  Y.,  Adley  M.D.,  Prat  P.C.,  Akers  S.A., Microplane model for concrete: II: data delocalization and verification, Journal of Engineering Mechanics, 122 (1996) 255–262. DOI: 10.1061/(ASCE)0733-9399(1996)122:3(255)
•  Chang  C.S.,  Misra  A., Packing structure and mechanical-properties of granulates, Journal of Engineering Mechanics, 116 (1990) 1077–1093. DOI: 10.1061/(Asce)0733-9399(1990)116:5(1077)
•  Cordero  N.M.,  Forest  S.,  Busso  E.P., Generalised continuum modelling of grain size effects in polycrystals, Comptes Rendus Mécanique, 340 (2012) 261–274. DOI: 10.1016/j.crme.2012.02.009
•  Cordero  N.M.,  Gaubert  A.,  Forest  S.,  Busso  E.P.,  Gallerneau  F.,  Kruch  S., Size effects in generalised continuum crystal plasticity for two-phase laminates, Journal of the Mechanics and Physics of Solids, 58 (2010) 1963–1994. DOI: 10.1016/j.jmps.2010.06.012
•  dell’Isola  F.,  Maier  G.,  Perego  U.,  Andreaus  U.,  Esposito  R.,  Forest  S., The complete works of Gabrio Piola: Volume I: Commented English Translation-English and Italian Edition, Springer International Publishing, 2014, ISBN: 978-3-319-00262-0
•  Digby  P.J., The effective elastic-moduli of porous granular rocks, Journal of Applied Mechanics-Transactions of the ASME, 48 (1981) 803–808. DOI: 10.1115/1.3157738
•  Duffy  J.,  Mindlin  R.D., Stress-strain relations and vibrations of a granular medium, Journal of Applied Mechanics, 24 (1957) 585–593.
•  Eugster  S.R.,  dell’Isola  F., Exegesis of the introduction and Sect. I from “Fundamentals of the Mechanics of Continua” by E. Hellinger, ZAMM—Journal of Applied Mathematics and Mechanics, 97 (2017) 477–506. DOI: 10.1002/zamm.201600108
•  Fredrich  J.T.,  Evans  B.,  Wong  T.F., Effect of grain-size on brittle and semibrittle strength—implications for micromechanical modeling of failure in compression, Journal of Geophysical Research-Solid Earth and Planets, 95 (1990) 10907–10920. DOI: 10.1029/JB095iB07p10907
•  Giorgio  I.,  Scerrato  D., Multi-scale concrete model with rate-dependent internal friction, European Journal of Environmental and Civil Engineering, 21 (2017) 821–839. DOI: 10.1080/19648189.2016.1144539
•  Gonzalez  M.,  Cuitino  A.M., A nonlocal contact formulation for confined granular systems, Journal of the Mechanics and Physics of Solids, 60 (2012) 333–350. DOI: 10.1016/j.jmps.2011.10.004
•  Hara  G., Theorie der akustischen Schwingungsausbreitung in gekornten Substanzen und experimentelle Untersuchungen an Kohlepulver, Elektrische Nachrichten Technik, 12 (1935) 191–200.
•  Hentz  S.,  Daudeville  L.,  Donze  F.V., Identification and validation of a discrete element model for concrete, Journal of Engineering Mechanics-Asce, 130 (2004) 709–719. DOI: 10.1061/(Asce)0733-9399(2004)130:6(709)
•  Jia  D.,  Ramesh  K.T.,  Ma  E., Effects of nanocrystalline and ultrafine grain sizes on constitutive behavior and shear bands in iron, Acta Materialia, 51 (2003) 3495–3509. DOI: 10.1016/S1359-6454(03)00169-1
•  Jia  H.,  Misra  A.,  Poorsolhjouy  P.,  Liu  C., Optimal structural topology of materials with micro-scale tension-compression asymmetry simulated using granular micromechanics, Materials & Design, 115 (2017) 422–432. DOI: 10.1016/j.matdes.2016.11.059
•  Mahboubi  A.,  Ajorloo  A., Experimental study of the mechanical behavior of plastic concrete in triaxial compression, Cement and Concrete Research, 35 (2005) 412–419. DOI: 10.1016/j.cemconres.2004.09.011
•  Misra  A.,  Chang  C.S., Effective elastic-moduli of heterogeneous granular solids, International Journal of Solids and Structures, 30 (1993) 2547–2566. DOI: 10.1016/0020-7683(93)90165-4
•  Misra  A.,  Ching  W.Y., Theoretical nonlinear response of complex single crystal under multi-axial tensile loading, Scientific Reports, 3 (2013) 1488. DOI: 10.1038/srep01488
•  Misra  A.,  Nejadsadeghi  N.,  De Angelo  M.,  Placidi  L., Chiral metamaterial predicted by granular micromechanics: verified with 1D example synthesized using additive manufacturing, Continuum Mechanics and Thermodynamics, (2020) DOI: 10.1007/s00161-020-00862-8
•  Misra  A.,  Placidi  L.,  Turco  E., Variational methods for discrete models of granular materials, in:  Altenbach  H.,  Öchsner  A. (Eds.), Encyclopedia of Continuum Mechanics, Springer Berlin Heidelberg, Berlin, Heidelberg, 2018, pp. 1–14, ISBN: 978-3-662-53605-6. DOI: 10.1007/978-3-662-53605-6_172-1
•  Misra  A.,  Placidi  L.,  Turco  E., Variational methods for continuum models of granular materials, in:  Altenbach  H.,  Öchsner  A. (Eds.), Encyclopedia of Continuum Mechanics, Springer Berlin Heidelberg, Berlin, Heidelberg, 2019, pp. 1–11, ISBN: 978-3-662-53605-6. DOI: 10.1007/978-3-662-53605-6_343-1
•  Misra  A.,  Poorsolhjouy  P., Granular micromechanics model for damage and plasticity of cementitious materials based upon thermomechanics, Mathematics and Mechanics of Solids, (2015a) 1081286515576821. DOI: 10.1177/1081286515576821
•  Misra  A.,  Poorsolhjouy  P., Identification of higher-order elastic constants for grain assemblies based upon granular micromechanics, Mathematics and Mechanics of Complex Systems, 3 (2015b) 285–308. DOI: 10.2140/memocs.2015.3.285
•  Misra  A.,  Poorsolhjouy  P., Elastic behavior of 2D grain packing modeled as micromorphic media based on granular micromechanics, Journal of Engineering Mechanics, 143 (2016a) C4016005.DOI: 10.1061/(ASCE)EM.1943-7889.0001060
•  Misra  A.,  Poorsolhjouy  P., Granular micromechanics based micromorphic model predicts frequency band gaps, Continuum Mechanics and Thermodynamics, 28 (2016b) 215–234. DOI: 10.1007/s00161-015-0420-y
•  Misra  A.,  Poorsolhjouy  P., Granular micromechanics model of anisotropic elasticity derived from Gibbs potential, Acta Mechanica, 227 (2016c) 1393–1413. DOI: 10.1007/s00707-016-1560-2
•  Misra  A.,  Singh  V., Nonlinear granular micromechanics model for multi-axial rate-dependent behavior, International Journal of Solids and Structures, 51 (2014a) 2272–2282. DOI: 10.1016/j.ijsolstr.2014.02.034
•  Misra  A.,  Singh  V., Thermomechanics-based nonlinear rate-dependent coupled damage-plasticity granular micromechanics model, Continuum Mechanics and Thermodynamics, 27 (2014b) 787–817. DOI: 10.1007/s00161-014-0360-y
•  Nejadsadeghi  N.,  Misra  A., Extended granular micromechanics approach: a micromorphic theory of degree n, Mathematics and Mechanics of Solids, 25 (2020) 407–429. DOI: 10.1177/1081286519879479
•  Placidi  L.,  Barchiesi  E., Energy approach to brittle fracture in strain-gradient modelling, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 474 (2018) 20170878. DOI: 10.1098/rspa.2017.0878
•  Placidi  L.,  Barchiesi  E.,  Misra  A., A strain gradient variational approach to damage: a comparison with damage gradient models and numerical results, Mathematics and Mechanics of Complex Systems, 6 (2018a) 77–100. DOI: 10.2140/memocs.2018.6.77
•  Placidi  L.,  Misra  A.,  Barchiesi  E., Two-dimensional strain gradient damage modeling: a variational approach, Zeitschrift für angewandte Mathematik und Physik, 69 (2018b) 56. DOI: 10.1007/s00033-018-0947-4
•  Poorsolhjouy  P.,  Misra  A., Effect of intermediate principal stress and loading-path on failure of cementitious materials using granular micromechanics, International Journal of Solids and Structures, 108 (2017) 139–152. DOI: 10.1016/j.ijsolstr.2016.12.005
•  Poorsolhjouy  P.,  Misra  A., Granular micromechanics based continuum model for grain rotations and grain rotation waves, Journal of the Mechanics and Physics of Solids, 129 (2019) 244–260. DOI: 10.1016/j.jmps.2019.05.012
•  Qomi  M.J.A.,  Krakowiak  K.J.,  Bauchy  M.,  Stewart  K.L.,  Shahsavari  R.,  Jagannathan  D.,  Brommer  D.B.,  Baronnet  A.,  Buehler  M.J.,  Yip  S.,  Ulm  F.J.,  Van Vliet  K.J.,  Pellenq  R.J.M., Combinatorial molecular optimization of cement hydrates, Nature Communications, 5 (2014) 4960. DOI: 10.1038/ncomms5960
•  Sfer  D.,  Carol  I.,  Gettu  R.,  Etse  G., Study of the behavior of concrete under triaxial compression, Journal of Engineering Mechanics-Asce, 128 (2002) 156–163. DOI: 10.1061/(Asce)0733-9399(2002)128:2(156)
•  Tavarez  F.A.,  Plesha  M.E., Discrete element method for modelling solid and particulate materials, International Journal for Numerical Methods in Engineering, 70 (2007) 379–404. DOI: 10.1002/nme.1881
•  Turco  E.,  dell’Isola  F.,  Misra  A., A nonlinear Lagrangian particle model for grains assemblies including grain relative rotations, International Journal for Numerical and Analytical Methods in Geomechanics, 43 (2019) 1051–1079. DOI: 10.1002/nag.2915
•  Walton  K., The effective elastic-moduli of a random packing of spheres, Journal of the Mechanics and Physics of Solids, 35 (1987) 213–226. DOI: 10.1016/0022-5096(87)90036-6
•  Ziegler  H., An Introduction to Thermomechanics, 2nd edition, North-Holland, Amsterdam, 1983, ISBN: 9780444598936.

Nomenclature

B_n, B_w

damage parameters in the normal and tangential directions

C_ijkl

fourth rank stiffness tensor

d₁, d₂

grain-sizes

D_i, D_n, D_w

grain-pair damage vector and normal and tangential components

D_ij

continuum damage tensor

E_n

normal stiffness parameter

f_i, f_n, f_w

grain-pair force vector and normal and tangential components

G_w

tangential stiffness parameter

k_ij, k_n, k_w

grain-pair stiffness tensor and normal and tangential components

l_i, l

grain-pair branch vector and branch length

n_i

unit vector in the direction of grain-pair branch vector

N

total number of grain

N_c

total number of grain-pair interactions

R

compression-tension ratio

s_i

unit vector on the plane orthogonal to grain-pair branch vector forming

t_i

unit vector on the plane orthogonal to grain-pair branch vector forming

W, W_n, W_w

macro-scale, normal and tangential grain-pair Helmholtz free energy density

Y

generalized force conjugate to grain-pair damage

Z

generalized force conjugate to grain-pair plastic displacements

α

size scaling parameter for grain-pair volumetric number density

α₁, α₂, α₃, α₄

model parameters controlling damage

β

size scaling parameter for grain-pair initial stiffness

γ

size scaling parameter for grain-pair damage parameters

δ_i, δ_n, δ_w

grain-pair displacement vector and normal and tangential components

ɛ_ij

infinitesimal strain tensor

φ

spherical coordinate

σ_ij

Cauchy stress tensor

θ

spherical coordinate

ψ, ψ_n, ψ_w

macro-scale, normal and tangential grain-pair dissipation potential

Authors’ Short Biographies

Payam Poorsolhjouy

Payam Poorsolhjouy is an Assistant Professor in the Chair of Applied Mechanics at Eindhoven University of Technology. His research interest is multiscale modeling and design of materials with complicated microstructure. He received his PhD in Civil Engineering with honors and as the Outstanding PhD graduate of the School of Engineering, from University of Kansas in 2016. He then joined Purdue University as a PostDoc working on multiscale material modeling. Prior to joining TU/e he was a University Assistant at Graz University of Technology. He has co-authored multiple journal papers and presented his research in various national and international conferences.

Anil Misra

Anil Misra is Professor of Civil Engineering and Associate Director of the Bioengineering Research Center at the University of Kansas, Lawrence. He has more than 30 years of experience in the area of multi-scale modeling, constitutive behavior of interfaces, granular soils and cement/asphalt concrete, and multi-modal material characterization using high-resolution techniques. He has pioneered the method of granular micromechanics. He has co-edited four books, guest edited five journal special issue, and authored more than 300 papers in journals, edited books and conference proceedings. He serves as a reviewer for multiple journals, extramural funding agencies and provides consulting services to industry.