2023 Volume 64 Issue 9 Pages 2202-2205
2023 Volume 64 Issue 9 Pages 2202-2205
In the present study, we investigated a finite element simulation considering the martensite transformation and transformation-induced plasticity (TRIP) to predict the quench distortion of a cut-cylinder 4340 steel. The distortion predicted by the finite element simulation considering both the martensite transformation and TRIP showed good quantitative agreement with the measured results. We analyzed the effects of the martensite transformation and TRIP on the quench distortion separately and concluded that TRIP has a very critical impact on the quench distortion of cut-cylinder 4340 steel. In addition, the chemical composition and quenching condition were confirmed to be important factors influencing the quench distortion even though the same cut-cylinder sample was used.
Heat treatment of metals is an effective means to obtain desired physical and mechanical properties through the design of the microstructure. However, temperature changes due to a mass effect during rapid heating or rapid cooling frequently cause problems such as shape distortion, cracking, and fracture. In the case of steels in which phase transformation occurs during heat treatment, the volume change due to the phase transformation causes excessive distortion along with thermal stress. Consequently, cracks occur occasionally, and in severe cases, the steel part even breaks.
Several studies have conducted heat treatment simulations through finite element analysis of the phase transformation in steels.1–5) Inoue and Arimoto1) first reported a heat treatment simulation system based on metallo-thermo-mechanics by using the finite element method. Ferguson et al.2) introduced a commercial heat treatment simulation software package to simulate heat treatment processes including phase transformation kinetics in various steel processes. Lee and Lee3) proposed a finite element code to explain the relationship between the transformation kinetics and distortion during oil quenching of a cut-cylinder 5120 sample. Şimşir and Gür4) developed a framework based on the finite element method to predict the heat transfer, microstructure, and stress during heat treatment. Lee et al.5) compared a finite element subroutine code with the commercial heat treatment code DANTE for the carburizing process to predict the quench distortion, microstructure, and other properties.
Many studies have mostly focused on the importance of the phase transformation from a mechanics viewpoint. The phase transformation from high-temperature face-centered cubic (FCC) austenite to low-temperature body-centered cubic (BCC) ferrite or body-centered tetragonal (BCT) martensite during cooling results in a volume change owing to the difference in the density of each phase. At the same time, an additional plastic strain called transformation-induced plasticity (TRIP) occurs when an internal stress is applied during the phase transformation of austenite. However, few studies have performed quantitative comparisons between the effect of the phase transformation volume and the effect of TRIP on the final distortion after heat treatment of steels. To address this gap, in the present study, we simulated the heat treatment process of an asymmetric cut-cylinder sample to show the distortion due to martensite transformation during quenching through finite element analysis.
An FCC austenite phase existing at high temperature and a BCT martensite phase existing at low temperature were investigated in this study. This is because the applied cooling condition is fast enough to suppress the occurrence of diffusional transformations such as ferrite, pearlite, or bainite during cooling.
The kinetics model for austenite formation from martensite during heating was derived from the modified model proposed by Boyadjiev et al.6) They expressed the incubation time used in the Avrami-type diffusion equation under isothermal cooling conditions as the phase transformation start temperature and completion temperature. Here, the phase transformation start temperature and completion temperature are those measured at the given cooling rate. If this model is applied to the continuous heating condition, it can be expressed as follows:
| \begin{equation} V_{A} = 1 - \exp \left(-b \left(\frac{T - A_{c1}}{A_{c3} - A_{c1}}\right)^{m} \right) \end{equation} | (1) |
Lee and Van Tyne proposed the following kinetics model for martensite formation from austenite decomposition during cooling:7)
| \begin{equation} V_{M} = 1 - \exp (-k(M_{S} - T)^{n}) \end{equation} | (2) |
The strain that occurs during heat treatment is caused by elastic and plastic strains and by the thermal strain due to temperature change. When a phase transformation occurs during heat treatment, volume expansion or contraction occurs owing to the resulting change in the density of each phase. Additional plastic strain, namely, TRIP strain, occurs when a tensile or compressive stress is applied during the phase transformation. In most cases, an internal stress is low enough to satisfy the linear relationship between the TRIP strain and the stress level. For ease of calculation, the following simplified TRIP equation with a TRIP parameter (K) including unspecified properties such as the yield stress of the weaker phase has been widely used for the finite element simulation of heat treatment:10,11)
| \begin{equation} \varepsilon^{tr} = K \cdot \sigma \cdot f(V) \end{equation} | (3) |
The commercial software DEFORM-3D was used for the finite element simulation. Phase transformation analysis was performed simultaneously by using the HT-module. Figure 1 shows the cut-cylinder shape used in this study. It is cut in the length direction at one-fourth of the diameter of a cylinder rod with a length and diameter of 160 mm and 20 mm, respectively. For speeding up the calculation, only half of the symmetry plane was actually analyzed. A tetrahedral mesh with 6422 nodes and 27320 elements was used.

Shape and dimension of cut-cylinder sample.
AISI 4340 steel was used for verification; it is a medium-carbon and low-alloy steel that is widely used for heat treatments such as quenching and tempering. The chemical composition of the AISI 4340 steel used in this study is Fe–0.409C–0.230Si–0.695Mn–0.0094P–0.0137S–0.169Cu–1.652Ni–0.672Cr–0.154Mo–0.015Al (in mass%). A hot-forged bar sample was machined as shown in Fig. 1 and heated in a box furnace from ambient temperature to 900°C. After being held at 900°C for 10 min, it was immediately water-cooled.
The material property data for the simulation were generated using the commercial software JMatPro (v13.1, General Steel database). A surface heat transfer coefficient of 5000 kW/mK was used for water cooling as mentioned in the literature.12)
Figure 2 shows a comparison of the measured time-temperature curve and the one predicted during cooling. The temperature change was measured by attaching a thermocouple to the center of the cut surface of the cut-cylinder specimen. Initially, the temperature decreased rapidly owing to water cooling. The cooling rate decreased owing to the latent heat generated during the martensite transformation, and an exothermic effect was observed at around 276°C, where MS is calculated by the formula.8) This confirmed that the kinetics models used in the simulation for the martensite transformation are quite reliable. A rather slow cooling was followed by convection cooling below MS.13) The microstructure in Fig. 1 shows the fully martensite of the quenched sample, and only martensite transformation is seen to occur with rapid cooling.

Measured time-temperature curve (open circle) compared with predicted curve (solid line). Inset shows the martensite microstructure from the quenched sample.
Figure 3 shows a simulation result predicting the shape of the distorted cut-cylinder sample in the final cooled state. It was gradually bent in the cutting plane direction (-y direction) along the length direction, and maximum deformation occurred up to approximately 309 µm. This result is opposite that of similar results reported by Lee and Lee.3) They reported that performing oil quenching on a cut-cylinder sample of the same shape and made of AISI 5120 steel, a Cr-added low-carbon low-alloy steel, resulted in a similar distortion in the round plane direction but not in the cutting plane direction. The contrasting result is obtained because AISI 4340 steel has a 0.4 mass% carbon content that is two times the 0.2 mass% carbon content of AISI 5120 steel, and consequently, it has relatively high hardenability. Therefore, in the cut-cylinder sample of AISI 5120 steel, some amount of bainite was generated during oil cooling, and the martensite transformation started at a higher temperature than 276°C. This means that the strength of the parent phase, namely, austenite, is also relatively low, resulting in different mechanical behaviors. In addition, the lower carbon content causes less phase transformation strain even if martensite transformation occurs in the same fraction. Of course, the additionally generated TRIP strain also has a different value. Owing to these complex mechanisms, the quench distortion behavior may show the opposite result depending on the phase transformation characteristics during cooling owing to the differences in the chemical composition and cooling rate even though the cut-cylinder sample has the same shape and same dimension. Therefore, finding a perfect solution for the quenching distortion problem remains difficult.

Simulation result of distorted shape after quenching. The initial shape is overlapped.
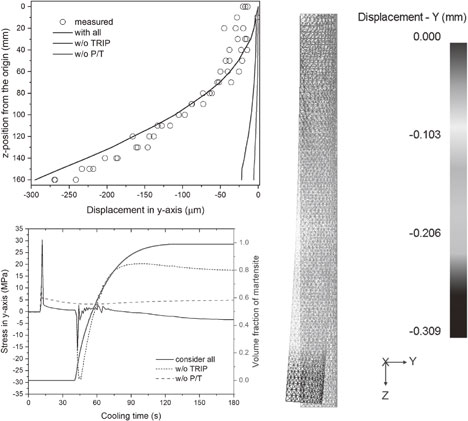
Figure 4 shows a comparison of the final deformation result of the cut-cylinder sample predicted by the simulation and obtained through actual measurements. The shape changes of the cut-cylinder sample before and after heat treatment were measured using a contact-type 3D measuring machine having a resolution of 100 nm. The simulation results considering both the density change due to martensite transformation during cooling and the additional strain due to the TRIP plasticity show very good agreement with the measured results. The red dashed line indicates the simulation result when only the density change due to martensite transformation is considered without considering the TRIP strain additionally generated during martensite transformation. The distortion direction toward the -y direction was predicted correctly; however, the predicted deformation level was very low, being around one-tenth the actual level. This reveals the critical effect of the TRIP strain on quench distortion. Several researchers have already reported on the importance of TRIP on deformation in steel heat treatment, and the results obtained in this study support these previous claims. If only the thermal stress due to elastoplasticity and thermal expansion/contraction are considered without even considering the martensite transformation, only a slight distortion, as indicated by the green dash dot line, is expected.
Effects of martensite transformation and transformation plasticity on quench distortion. Solid lines and open circles represent calculated and measured results, respectively.
Figure 5 shows the stress change when martensite transformation occurs during cooling. After 10 s of cooling, tensile stress is formed by thermal contraction. After approximately 40 s, martensite transformation starts and expansion occurs from FCC to BCT; therefore, compressive stress forms instantaneously. However, different stress change behaviors are seen subsequently depending on whether TRIP strain is considered. While a new phase (i.e., martensite) is generated during cooling, the TRIP strain occurs additionally depending on the stress type: tensile strain is generated under tensile stress, and compressive strain is generated under compressive stress. Therefore, it is affected by the stress change according to the generated TRIP, and it shows a serration as indicated by the black line. When TRIP is not considered, the stress simply changes in proportion to the increase in the martensite volume fraction. In this study, both the martensitic transformation and TRIP characteristics were investigated using relatively simple cut-cylinder samples.
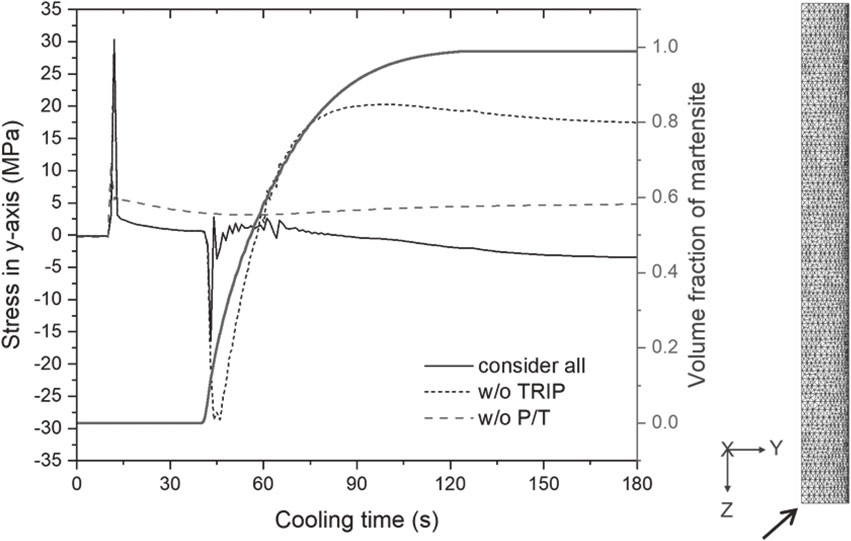
Variation of stress during quenching considering the effects of the martensite transformation and transformation plasticity. The arrow indicates the prediction edge point.
In this study, a finite element simulation was conducted to predict the quench distortion of a cut-cylinder 4340 specimen during rapid cooling by considering the phase transformation. Based on the simulation results, the following conclusions were obtained.