Representation of Nye’s Lattice Curvature Tensor by Log Angles

Abstract

The log angles of a rotation matrix are three independent elements of the logarithm of the rotation matrix. Nye’s lattice curvature tensor κ_ij is discussed by using the log angles. For the change in a crystal orientation ΔR with the change in a position Δx_i, it is shown that the elements of κ_ij are written as κ_ij = Δω_i/Δx_j using the log angles Δω_i of ΔR. The log angles for the crystal rotation given by the axis/angle pair are also discussed.

 

This Paper was Originally Published in Japanese in J. Japan Inst. Met. Mater. 82 (2018) 415–418.

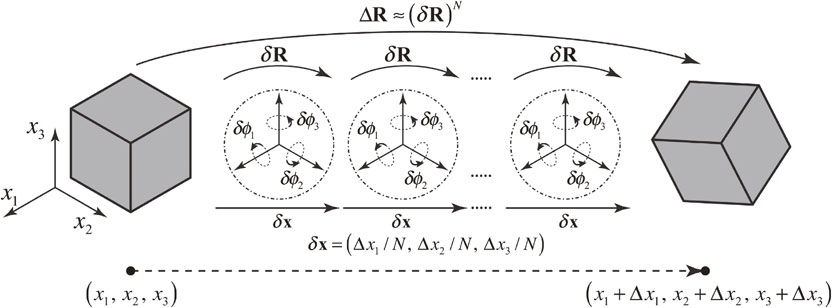
Fig. 2 The change in a crystal orientation as much as ΔR with the change in a position from (x₁, x₂, x₃) to (x₁ + Δx₁, x₂ + Δx₂, x₃ + Δx₃). δR is a small-angle rotation which satisfies ΔR ≈ (δR)^N where N is a sufficiently large positive integer. The relationship ΔR ≈ (δR)^N means that the N-times successive rotations of δR with an interval of δx = (Δx₁/N, Δx₂/N, Δx₃/N) is equivalent to ΔR. The angles δϕ_i are the small rotation angles of δR around the x_i axes.