分子動力学法を用いた熱輸送解析：後退接触線の冷却現象

概要

固体表面と気液界面の交線である接触線が移動する際，前進側と後退側で接触角が変化することが広く知られている．これに加えて，非平衡分子動力学解析（NEMD）により，前進接触線と後退接触線で生じる熱的な差が明らかになった．液体のバルクについては粘性散逸により発熱することが予想され，同様に前進接触線では温度が上昇する一方，後退接触線では予想に反して温度が低下することが示された．本文では，NEMDを用いた熱輸送解析手法，および，後退接触線での冷却メカニズムについて紹介する．

1　 はじめに

濡れ現象は我々人間の日常生活，自然，様々な科学・工学分野などの至る所に存在している．特に，濡れ性を決定するうえで重要な固体・気体・液体の三相が交わる接触線の振る舞いに対する理解とそれに基づく現象制御が重要視されてきている．マクロスケールの平衡状態の接触線にはたらく力のつり合い式として，1805年にYoungの式［1］が定式化されて以降，濡れ現象は広く研究の対象として扱われてきた．静的接触線においては，固液・固気・気液界面張力が壁面接線方向につりあうことで，気液界面と固体面のなす角である接触角が決定され，濡れ性の指標として用いられる．この平衡状態の濡れ現象について，1980年代以降の計算機による数値解析の発展とともに，分子動力学解析（MD）を用いたミクロスケールの解析も行われるようになった［2］．また，著者を含む研究によって，ミクロスケールの静的接触線を含む検査体積に対する力のつり合いが最終的には上述のYoungの式に帰結することがわかった［3］．

静的濡れに対して，固体壁面上を動的に移動する接触線は動的接触線と呼ばれる．動的な濡れ広がりやその接触線の移動の過程では，静的な場合とは異なり，前進側と後退側の接触角が異なるという前進・後退という効果が現れることが知られており，これまでに多くの理論的・数値的・実験的研究［4］がなされてきた．固液摩擦と粘性応力が前進・後退の接触角の差異を引き起こしていることがわかってきたが，その動的接触線の支配原理は未解明である．動的接触線の差異は，ナノスケールの力の不釣り合いに起因するものであり，連続体の保存則と整合する形でナノスケールの動的濡れ現象の解析を行うべきだが，そのような取り組みは少なく，この動的濡れ現象は流体力学の未解明問題のひとつであると言える．

本記事では，動的濡れ過程時に生じる接触角の差異に加えて，前進・後退接触線が各々加熱・冷却するという熱的な差異を示す．そして，その熱的な差異のメカニズムを解明するために，非平衡分子動力学法で連続体の保存則と整合する形で熱輸送現象を解析する手法を導出し，定量的に動的濡れ過程時に誘起される後退接触線の冷却という特異な熱輸送現象のメカニズムを定量的に解き明かす．なお，本記事は，ナノスケールの動的濡れ現象の解析手法・解析結果を示した著者による研究［5］の内容をまとめたものである．

2　 熱輸送解析手法

分子動力学法（MD）で巨視的な流れ場を解析する際，瞬間的には，連続体ではなく離散的に存在する分子の微視的（ミクロ）なふるまいを平均化する必要がある．また，平均化することで得られる巨視的（マクロ）な流れ場において，応力テンソルや熱流束の分布が重要な役割を担う．例えば連続体を仮定する流体力学では，構成方程式によって応力テンソルが決定され，流体の局所の加速度は，その応力の勾配を含むかたちで決定される．これに対してMDで取り扱うミクロな系では，分子の動きは分子間相互作用力によって決定され，応力テンソルや熱流束は分子の動きと分子間相互作用力により定義される．本章では，マクロの流体力学で用いられる保存則，すなわち，連続体の保存則に矛盾しない形で，非平衡分子動力学解析（NEMD）において熱輸送現象を解析する手法を紹介する．具体的には，検査面の方法（Method of Plane, MoP）［6–8］を用いて，ToddやDaivisら［9］による単一流体系で熱流を算出する手法を，壁面を含む多成分系に拡張することを考える．まず，外力ありの連続体のエネルギー保存則は次式で与えられる．

  

$$\frac{\partial \rho e}{\partial t}=-\nabla ·(\rho e\mathit{u}+{\mathit{J}}_Q-\mathit{\tau }·\mathit{u})+\rho F^{\mathrm{ext}}·\mathit{u}$$(1)

ここで$\rho ,e,\mathit{u}$は各々流体の密度，流体の持つ単位質量当たりのエネルギー，速度であり，${\mathit{J}}_{\mathrm{Q}},\mathit{\tau },{\mathit{F}}^{\mathrm{ext}}$は各々熱流束，応力テンソル，流体が受ける単位質量あたりの外力である．なお，本研究では，流体–流体間の相互作用力は応力テンソル$\mathit{\tau }$に寄与する一方，流体–固体間の相互作用力は（流体に対する）外力，すなわち，体積力$\rho {\mathit{F}}^{\mathrm{ext}}$として取り扱われる．この式(1)を任意の検査体積（CV）で体積積分しGaussの発散定理を適用することで，次式のCVに対するエネルギー保存則が得られる．

  

$$\begin{array}{cc}{\int }_{\mathrm{CV}}^{}\mathrm{d}V\frac{\partial \rho e}{\partial t}=& -{\int }_{\mathrm{CV}}^{}\mathrm{d}V\nabla ·{\mathit{J}}_{\mathrm{Q}}+{\int }_{\mathrm{CV}}^{}\mathrm{d}V\rho {\mathit{F}}^{\mathrm{ext}}·\mathit{u}\\ & -{\int }_{\mathrm{S}}^{}\mathrm{d}\mathit{S}·(\rho e\mathit{u}-\mathit{\tau }·\mathit{u})\hfill \end{array}$$(2)

これを変形することで

  

$$\begin{array}{cc}{\int }_{\mathrm{CV}}^{}\mathrm{d}V\nabla ·{\mathit{J}}_{\mathrm{Q}}=& -{\int }_{\mathrm{CV}}^{}\mathrm{d}V\frac{\partial \rho e}{\partial t}+{\int }_{\mathrm{CV}}^{}\mathrm{d}V\rho {\mathit{F}}^{\mathrm{ext}}·{\mathit{u}}^{\mathrm{VA}}\\ & -{\int }_{\mathrm{S}}^{}\mathrm{d}\mathit{S}·\rho e\mathit{u}+{\int }_{\mathrm{S}}^{}\mathrm{d}\mathit{S}·\mathit{\tau }·\mathit{u},\hfill \end{array}$$(3)

左辺のCVからの熱の流出，すなわちCV内での単位時間当たりの発熱量が，右辺第一項のCV内のエネルギーの時間変化，第二項のCV内の流体が受ける外力による仕事，第三項のCVの表面を通過する巨視的なエネルギーの移流の項，および第四項のCVの表面に作用する応力の仕事から求まることがわかる．ここで，外力は体積力$\rho {\mathit{F}}^{\mathrm{ext}}$として取り扱われるため，それと内積を取られる速度ベクトルには体積平均により求めたもの${\mathit{u}}^{\mathrm{VA}}$を採用する．NEMDにおいて，右辺第一項および第二項については体積平均の方法によって計算可能な一方，第三項および四項についてはMoP［8,10］で計算可能である．本研究では，これに基づいて流体の熱輸送解析を行う．

また，壁から十分遠い場所では，体積力である外力が作用しないため，検査面を通過するエネルギー流束は，検査面を通過する巨視的なエネルギーの移流項$\rho e\mathit{u}$，検査面に作用する応力仕事$\mathit{\tau }·\mathit{u}$，検査面を通過する熱流束$J_{\mathrm{Q}}$を用いて$\rho e\mathit{u}+{\mathit{J}}_{\mathrm{Q}}-\mathit{\tau }·\mathit{u}$と表される．検査面を通過するエネルギー流束はMoPを用いることで計算可能［11］で，これに基づくと，MoPを用いてエネルギー流束$\rho e\mathit{u}+{\mathit{J}}_{\mathrm{Q}}-\mathit{\tau }·\mathit{u}$，検査面を通過する巨視的なエネルギーの移流項$\rho e\mathit{u}$，検査面に作用する応力仕事$\mathit{\tau }·\mathit{u}$をすべて計算することで，検査面を通過する熱流束${\mathit{J}}_{\mathrm{Q}}$が逆算的に求まることになる．

3　 動的接触線の熱輸送現象

3.1　 計算系

本研究では，動的接触線近傍で誘起される熱輸送解析のために，図1上段に示すように，Arを模したLennard-Jones（LJ）液体をFCC構造のふたつの壁面ではさみ，さらに各々x軸正方向に10 m/sおよび−10 m/sで動かすことで，前進・後退接触線を有する定常の非平衡分子動力学系を実現した．せん断系の定常状態を保つためには，粘性散逸に起因する熱を適切に取り除く必要があり，固体壁の最外層から二層目の壁面原子をLangevin熱浴法を用いて85 Kに温度制御をした．なお，固体原子–流体分子間にもLJポテンシャルを作用させ，85 Kにおける静的接触角が約57度になるように，固体原子–流体分子間の相互作用パラメータを決定している．運動方程式の数値積分には速度Verlet法を用い，その時間刻みは$\mathrm{\Delta }t=5$ fsとした．本研究で行う熱輸送解析では400 nsの時間平均を用いており，式(3)の右辺第三項および第四項に含まれる応力テンソル，それと内積を取られる検査面上での速度ベクトル，エネルギーの移流の項はすべてMoPで計算をしており，zx平面上で$\mathrm{\Delta }z=0.149$ nmおよび$\mathrm{\Delta }x=0.150$ nm間隔に系を分割することで得られるx，z-方向に法線ベクトルを有する長方形の検査面を用いた．また，式(3)の右辺第一項および第二項に含まれる流体の持つエネルギーの時間変化の項，外力，および体積力と内積を施される速度ベクトルに関しては，同様の間隔で系を分割することで得られる検査体積を用いて体積平均の方法で計算した．

図1  （上段）：Lennard-Jones流体からなる動的接触線を有する準二次元非平衡分子動力学系．（中段）：密度および速度の分布．（下段）：温度分布．[Reprinted from Ref. [5]; licensed under Creative Commons CC-BY license.]

3.2　 計算結果

図1中段に体積平均の方法で求めた密度および速度分布を示す．壁によるせん断によって，液体内部では時計回りのキャタピラー型の流れ場が形成され，それによって見かけの接触角が異なる前進側（図中右下および左上）および後退側（図中右上および左下）の接触線が現れた．本研究では，この前進・後退の接触角の差異だけではなく，図1下段に示す温度分布に現れる熱的な差異，すなわち，前進接触線（図中右下および左上）では温度がバルクに対して上昇していることに対して，後退接触線（図中右上および左下）では温度が下降していることについて取り扱う．各界面から十分遠いバルク液体とみなせる領域は概ね86.5 Kであり，これは壁面の制御温度85 Kよりわずかに高く，粘性散逸が引き起こす発熱によるものである．一方，前進接触線ではバルクに対して2 Kほど高温で，後退接触線では2 Kほど低温であることが図中からわかる．通常せん断下のバルクにおいて生じる粘性散逸は発熱，すなわち，温度上昇しか引き起こさない一方で，後退接触線においては冷却が生じている点が直観に反しているため興味深く，動的接触線近傍の熱輸送現象には別のメカニズムが隠されていることが示唆される．

この動的接触線近傍で誘起されている特異な熱輸送現象を解き明かすために，本研究では，図2に示す熱輸送解析を行った．図2上段は温度分布および熱流束場を示したもので，発熱している前進接触線から後退接触線へ熱が流れ，そこで熱が吸収されていることが確認できる．なお，前章で述べた通り，固体壁面の影響が及ぶ範囲では，体積力による仕事が作用することで検査面上を通過する熱流束を求めることは難しくなるため，ここでは固体壁面近傍の熱流束を表示していない．

図2  マゼンタで示す3つの検査体積における（上段）：熱流束の発散，（中段）：応力テンソルと速度勾配テンソルの内積，（下段）：内部エネルギーのLagrange微分の体積積分値．さらに，（上段）温度と熱流束の分布を，（下段）内部エネルギーと速度の分布を示す．[Reprinted from Ref. [5]; licensed under Creative Commons CC-BY license.]

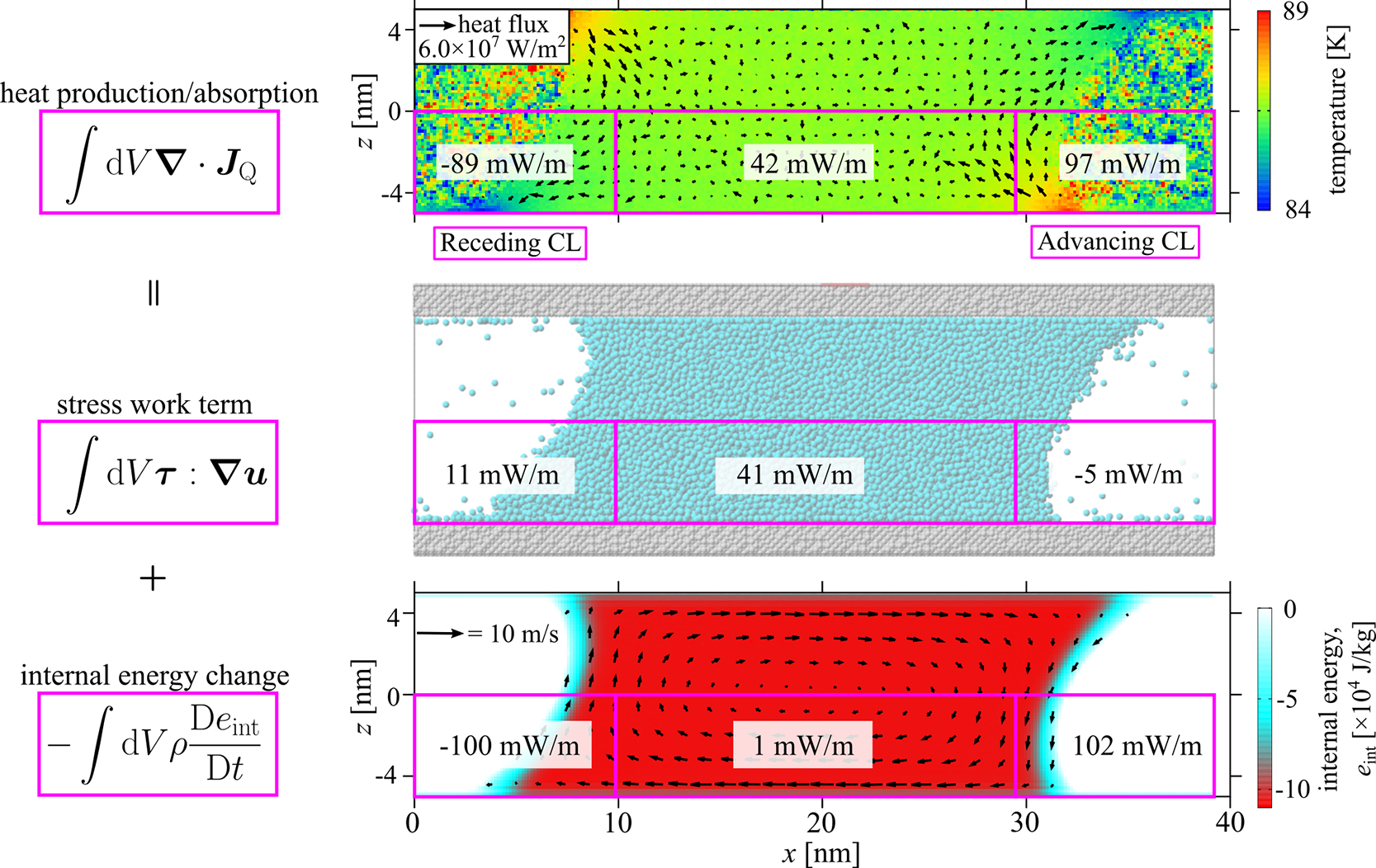
発熱・吸熱量を定量的に見積もるために，図2にマゼンタで示すように，各々前進接触線，後退接触線，液体バルクを含むような3つの検査体積を設定し，熱流束の発散の体積積分を式(3)を用いて計算し，その積分値を図中の検査体積内に示す．なお，単位は奥行き長さ当たり単位時間当たりの発熱量とし，mW/mで示している．図2上段から，前進接触線では熱が生成（97 mW/m）され，後退接触線では熱が吸収（−89 mW/m）されている一方で，前進・後退接触線を囲む検査体積の2倍程度の検査体積を設定した液体バルク部では42 mW/mほどしか発熱されていないことがわかる．これにより確かに動的接触線近傍の発熱・吸熱機構は粘性散逸によるものではないことがわかる．

より詳細にこの特異な発熱・吸熱機構を調べるため，式(1)に示したエネルギー保存則を，質量・運動量保存則を用いて変形する．

  

$$\mathbf{\nabla }·{\mathit{J}}_{\mathrm{Q}}=\mathit{\tau }:\mathbf{\nabla }\mathit{u}-\rho \frac{\mathrm{D}{e}_{\mathrm{int}}}{\mathrm{D}t}$$(4)

なお，$\mathrm{D}/\mathrm{D}t$および$:$は各々Lagrange微分および二階のテンソルの内積を意味する．また，$e_{\mathrm{int}}$は次式で定義される単位質量当たりの流体のエネルギーから移流による巨視的な運動エネルギーを取り除いた内部エネルギーを意味し，流体–流体間だけでなく流体–固体間の相互作用エネルギーも含められるものである．

  

$$e_{\mathrm{int}}=e-\frac{1}{2}{\left|\mathit{u}\right|}^2$$(5)

式(4)により，流体の発熱・吸熱は次のふたつのメカニズム

1.　応力テンソルと速度勾配テンソルの内積

2.　流跡線に沿った内部エネルギーの変化

に分けられ，バルクにおいては，前者は粘性散逸に，後者は相変化に伴う潜熱の内部エネルギー項に相当することがわかる．巨視的に定常であることを仮定すると，式(4)の右辺第一項は運動量保存則を代入することで

  

$$\begin{array}{ccc}\mathit{\tau }:\mathbf{\nabla }\mathit{u}& =\mathbf{\nabla }·(\mathit{\tau }·\mathit{u})\hfill & -\mathit{u}·(\nabla ·\mathit{\tau })\hfill \\ & =\mathbf{\nabla }·(\mathit{\tau }·\mathit{u})\hfill & -\frac{\partial }{\partial t}\frac{1}{2}\rho {\left|\mathit{u}\right|}^2\hfill \\ & & -\mathbf{\nabla }·\frac{1}{2}\rho {\left|\mathit{u}\right|}^2\mathit{u}+\rho {\mathit{F}}^{\mathrm{ext}}·\mathit{u}\\ & =\mathbf{\nabla }·(\mathit{\tau }·\mathit{u})\hfill & -\mathbf{\nabla }·\frac{1}{2}\rho {\left|\mathit{u}\right|}^2\mathit{u}+\rho {\mathit{F}}^{\mathrm{ext}}·\mathit{u}\end{array}$$(6)

と変形できる．この式の右辺第一項および第二項の体積積分は，Gaussの発散定理を適用することで，MoPで計算した各流束を面積積分することで求まる一方で，右辺第三項については外力（流体が固体壁面から受ける体積力）による仕事を体積積分することで求まる．図2中段に，式(6)の積分結果を示す．液体バルク部での発熱はこの応力仕事の項が主要である，すなわち粘性散逸が主要である一方で，動的接触線を囲む検査体積ではそうではないことがわかる．さて，発熱・吸熱のもうひとつのメカニズムである式(4)の右辺第二項の，流跡線に沿った内部エネルギー変化の項については質量保存則を代入することで

  

$$\begin{array}{cc}-\rho \frac{\mathrm{D}{e}_{\mathrm{int}}}{\mathrm{D}t}& =-\frac{\partial \rho e_{\mathrm{int}}}{\partial t}-\mathbf{\nabla }·\rho e_{\mathrm{int}}\mathit{u}\hfill \\ & =-\frac{\partial \rho e}{\partial t}+\frac{\partial }{\partial t}\frac{1}{2}\rho {\left|\mathit{u}\right|}^2-\mathbf{\nabla }·\rho e\mathit{u}+\mathbf{\nabla }·\frac{1}{2}\rho {\left|\mathit{u}\right|}^2\mathit{u}\hfill \\ & =-\frac{\partial \rho e}{\partial t}-\mathbf{\nabla }·\rho e\mathit{u}+\mathbf{\nabla }·\frac{1}{2}\rho {\left|\mathit{u}\right|}^2\mathit{u},\hfill \end{array}$$(7)

と変形できる．なお，ここでも式(6)と同様に巨視的には定常であることを仮定した一方で，右辺第一項については，MDで時間平均をする際にサンプリング開始時と終了時の微視的な分子の揺らぎにより無視できない値を持つためあえて残した［8］．また，右辺第二項および第三項の体積積分はGaussの発散定理によりMoPで計算した流束を面積積分することで求まる一方で，右辺第一項については直接体積積分することで求まる．さて，この式(7)を体積積分した結果を，内部エネルギーと速度の分布と合わせて図2下段に示す．動的接触線近傍では流線に沿って内部エネルギーが変化していて，式(7)の積分結果からも，動的接触線近傍での発熱・吸熱は流線に沿った内部エネルギー変化による項が主要であることがわかる．つまり，前進接触線近傍では，流体が気液界面と固気界面から固液界面に流れる過程で発熱し，逆に，後退接触線近傍では，流体が固液界面から気液界面と固気界面に流れる過程で吸熱（冷却）する．これらの過程において，流体の内部エネルギーは，周囲の密度の変化と固体表面によって誘起されるポテンシャル場によって変化し，接触線近傍での発熱と吸熱につながることがわかる．流跡線に沿って，すなわちLagrange的視点で動的濡れ現象を捉えると，この加熱・冷却現象は動的接触線近傍で界面が変化することで引き起こされていて，相変化に伴う発熱・吸熱を引き起こす潜熱に類似する現象と解釈できる．

4　 まとめ

本記事では，非平衡分子動力学法（NEMD）における熱輸送の解析手法を紹介し，それに基づく，定常な動的接触線近傍での熱輸送解析結果を示した．特に，巨視的なエネルギー保存則と整合するかたちで導出したことによって，発熱・吸熱のメカニズムを，応力テンソルと速度勾配テンソルの内積の項と，内部エネルギーのLagrange微分，すなわち，流跡線に沿った内部エネルギーの変化の項のふたつで定量的に評価出来た．本記事で紹介したNEMDを用いた分子スケールの熱輸送解析手法は，準二次元系に制限されるものではなく三次元系においても適用可能であるため，今後カーボンナノチューブ内の動的濡れ現象などの解析にも期待できる．また，さらに，本解析手法は巨視的なエネルギー保存則と整合するかたちで導出されたものであるため，定常状態に制限されるものではなく，適切なアンサンブル平均を取ることで非定常な問題にも適用可能であり，非定常な動的濡れ広がり過程などの解析にも期待できる．

 謝辞

本研究はJSPS科研費23KJ0090の助成を受けたものです．また，本研究の数値計算は，東北大学流体科学研究所未来流体情報創造センターの次世代融合研究システム（AFI-NITY）を用いて行ったものです．ここに謝意を示します．

参考文献

• [1]   T.  Young, Philos. Trans. R. Soc. London, 95, 65 (1805).
• [2]   M. J. P.  Nijmeijer,  C.  Bruin,  A. F.  Bakker and  J. M. J.  Van Leeuwen, Phys. Rev. A, 42, 6052 (1990).
• [3]   Y.  Yamaguchi,  H.  Kusudo,  D.  Surblys,  T.  Omori and  G.  Kikugawa, J. Chem. Phys., 150, 044701 (2019).
• [4]   J. H.  Snoeijer and  B.  Andreotti, Annu. Rev. Fluid. Mech., 45, 269 (2013).
• [5]   H.  Kusudo,  T.  Omori,  L.  Joly and  Y.  Yamaguchi, J. Chem. Phys., 159, 161102 (2023).
• [6]   B. D.  Todd,  D. J.  Evans and  P. J.  Daivis, Phys. Rev. E, 52, 1627 (1995).
• [7]   B. D.  Todd,  P. J.  Daivis and  D. J.  Evans, Phys. Rev. E, 51, 4362 (1995).
• [8]   H.  Kusudo,  T.  Omori and  Y.  Yamaguchi, J. Chem. Phys., 155, 184103 (2021).
• [9]   B. D.  Todd and  P. J.  Daivis, Nonequilibrium Molecular Dynamics: Theory, Algorithms and Applications, Cambridge University Press (2017).
• [10]   P. J.  Daivis,  K. P.  Travis and  B. D.  Todd, J. Chem. Phys., 104, 9651 (1996).
• [11]   T.  Ohara, J. Chem. Phys., 111, 6492 (1999).

著者紹介

楠戸 宏城（博士（工学））

〔経歴〕2022年大阪大学工学研究科博士課程修了，2023年東北大学流体科学研究所に入所．2024年から現所属．〔専門〕熱力学，濡れ．〔趣味〕釣り．