金融資産の価格リターンとオーダー・フロー・インバランスの相互作用についての分析

要旨

本研究では、構造型ベクトル自己回帰（structural vector autoregressive：SVAR）モデルを用いて、S&P 500 E-mini先物のベスト・ビッド（最高値での買い注文）とベスト・オファー（最安値での売り注文）のファイルから計算されたオーダー・フロー・インバランス（買い注文と売り注文の差、order flow imbalance：OFI）と価格リターンの間の相互作用を分析する。よく知られている注文の数量などの市場変数の日内変動は、SVARモデルを1日の短い区間ごとに適用することで考慮し、一定区間で集計することによる内生性は、分散不均一性による識別（identification through heteroskedasticity：ITH）によって構造パラメータを推定することで処理した。ITHによる推定の結果、有意な内生性が存在すること、推定されたパラメータと関連する変量（OFIによって引き起こされるリターンの分散など）は市場変数の変動を反映して時間とともに変化することが示された。

Abstract

The study examines the interaction between returns and order flow imbalances (differences between buy and sell orders), constructed from the best (highest) bid and best (lowest) offer files of S&P 500 E-mini futures contract, using a structural vector autoregressive (SVAR) model. The well-known intraday variation in market variables such as the number and size of orders is considered by applying the SVAR model for each short interval each day, whereas the endogeneity due to time aggregation is handled by estimating the structural parameters via identification through heteroskedasticity. The results show that significant endogeneity exists and that the estimated parameters and associated variates, such as the return variance driven by order flow imbalances, vary over time, reflecting the movements in market variables.

1.  はじめに

現代の金融市場では、様々な価格における注文を集めた指値注文板（limit order book：LOB）が導入されている¹。LOBは指値注文、成行注文、未決済の指値注文のキャンセルなどの新規注文の到着によって更新される。このような注文によって引き起こされる価格の変化は、プライス・インパクトと呼ばれ、市場の流動性の1側面を反映している。このような価格変化は、トレーダーが価格連動型の取引戦略を採用している場合には、成行注文や指値注文、キャンセルを誘発することもある。このように、価格と注文の間の相互作用は、現代の金融市場における価格形成メカニズムを理解する上で不可欠である。そこで、本研究では、S&P E-mini 500先物取引のベスト・ビッド（最高値での買い注文）とベスト・オファー（最安値での売り注文）を記録したベスト・ビッド・アンド・オファー（best bid and offer：BBO）ファイルを用いて、価格と注文の相互作用を分析する。

金融市場における価格変化の要因は、マーケット・マイクロストラクチャーに関する研究において重要な課題であった。例えば、Hasbrouck（1991）は、価格変化が現在および過去の価格だけでなく、取引の規模や符号、ビッド・アスク・スプレッド（ベスト・ビッドとベスト・アスクの価格の差で流動性の代理変数）に依存することを示している。理論的には、これらの現象は情報の非対称性に起因するとされている²。取引や情報の流れが価格変化に与える影響については、Jones et al.（1994a, b）やEasley et al.（1997a, b）などが分析している。

Dufour and Engle（2000）は、Hasbrouck（1991）の価格と取引に関するベクトル自己回帰（vector autoregressive：VAR）モデルを拡張し、取引間隔が短くなると、取引のプライス・インパクト、取引関連情報に対する価格調整のスピード、符号付き取引（買い取引をプラス、売り取引をマイナスとした指標）の正の自己相関のすべてが増加することを示している。さらに、Chung et al.（2005）は、プライス・インパクトが、Easley and O’Hara（1992）が導入しEasley et al.（1997b）が発展させた、情報に基づく取引の確率（probability of information-based trading：PIN）という概念と正の相関関係があることを示している。プライス・インパクトに関する他のさまざまな側面については、Bouchaud et al.（2002）、Bouchaud et al.（2004）、Bouchaud et al.（2006）、Bouchaud et al.（2009）などで広範に研究されている。

最も高い頻度では、単一の注文のプライス・インパクトは、機械的な価格変化として測定され、LOBのデプス（未決済の買い注文と売り注文の数量）、特にBBOにおけるデプスに依存する。Hautsch and Huang（2012）は、気配値とデプスの共和分VARモデルを用いて、単一の注文のプライス・インパクトを分析している。このような機械的な価格変化は、Cont et al.（2014）が導入した単純化LOBモデルでも示されている。各注文の到着時間に基づいたデータであれば、変数の内生性を引き起こす可能性のある時間集計を避けて、単純にプライス・インパクトを測定することができる。

しかし、現代市場では、高度な技術とアルゴリズム取引システムにより、トレーダーは毎秒数百件の注文を出すことができる³。このような超高頻度では、各注文によって引き起こされる機械的な価格変化を追跡するためには膨大なデータの取得と分析が必要となる。また、Boehmer et al.（2005）が示したように、多くの指値注文は発注後すぐにキャンセルされるため、LOBが頻繁に変化し、単一の注文による機械的な価格変化の影響は信頼できない。したがって、数秒から数分といった短い区間で集計された注文のプライス・インパクトを測定または推定することは、より現実的で賢明である。

Cont et al.（2014）は、オーダー・フロー・インバランス（買い注文と売り注文の差、order flow imbalance：OFI）の価格への影響を10秒区間で推定している。彼らは、30分毎に価格変化をOFIに回帰し、プライス・インパクトの推定値（OFIの係数のOLS推定値）が彼らの提案した単純化LOBモデルと整合的であることを示した。また、プライス・インパクトの推定値は、市場が開いた（寄り付き）直後に高く、市場が閉まる（大引け）直前に小さくなるという顕著な日内パターンを示している。このパターンは、ボラティリティや取引量などについて先行研究で広く観察されているU字型やJ字型のパターンとは異なる⁴。

しかし、短い区間で集計された注文のプライス・インパクトを、単純な回帰により推定できるかどうかは議論の余地がある。価格連動型の注文戦略では、価格変化がその後の注文を誘発する可能性がある⁵。Deuskar and Johnson（2011）は、この内生性を考慮して、Rigobon（2003）、Rigobon and Sack（2003, 2004）、Sentana and Fiorentini（2001）によって提案された、分散不均一性による識別（identification through heteroskedasticity：ITH）を用いて、リターンとネット・オーダー・フロー（買い注文から売り注文を引いたもの）を同時定式化しプライス・インパクトを推定している⁶。さらに、Eisler et al.（2012）とHautsch and Huang（2012）は、価格変化と注文の複雑な系列相関および相互相関の構造を示している。

本研究では、こうした価格変化と注文の間の内生的かつ動的な相互作用を考慮し、構造型ベクトル自己回帰（structural vecotr autoregressive：SVAR）モデルによってS&P500 E-mini先物のBBOファイルから計算した中値のリターンとOFIの関係を分析する。具体的には、1日（シカゴ時間8:30～15:00）の15分ごとにSVARモデルをITHを利用して推定することで、日中の変動と内生性の両方を考慮してリターンとOFIの相互作用を分析した。

実証分析の結果、提案された手法は、リターンとOFIの複雑な系列相関および相互相関の構造を捉えるのに有効であることが示され、先行研究で提示されたいくつかの知見が確認された。特に、この分析では、1秒区間で有意なプライス・インパクト（OFIからリターンへの影響）とフロー・インパクト（リターンからOFIへの影響）が示された。この結果は、Deuskar and Johnson（2011）の結果と整合的であり、内生性によるOLS推定値の上方バイアスを裏付けるものとなっている。また、内生性を考慮してITHにより推定したプライス・インパクトは、Cont et al.（2014）の単純化LOBモデルが示唆するものと整合的であった。インパルス応答からは、リターンとOFIへのショックの影響のほとんどは1秒以内に消え、瞬間的な影響と長期的な影響は概ね同じ日内パターンを示した。さらに、推定されたパラメータとそれらの関数として算出される変量は、LOBのデプス、成行・指値注文およびキャンセルの数、平均スプレッドなどの変動に関連して有意な日内変動を示した。

本稿の以下の構成は次の通りである。まず、第2節で、S&P 500 E-mini先物取引のデータと変数の計算方法を紹介し、それらの基本統計量および日内変動を示す。続く第3節で、モデルと推定方法を説明し、第4節では、推定結果とインパルス応答分析を示す。さらに、第5節では、推定パラメータと関連する変量の日内変動を説明する。最後に、本稿のまとめを行う。

2.  データ

本研究で使用するデータは、CME Groupから入手したS&P 500 E-mini先物のBBOファイルから作成したものである⁷。BBOファイルには、ベスト・ビッドとベスト・アスクの価格または数量（サイズ）を変更するすべてのイベントが含まれている。具体的には、成行注文によって引き起こされたすべての取引と、指値注文やキャンセルによって引き起こされたすべての気配値の修正が含まれている。データ項目は、日付、限月、時間（秒）、取引シーケンス番号、イベント分類番号（0：アスク、1：ビッド、2：取引）、価格、数量である。1秒以内に複数のイベントが発生した場合は、その日固有の取引シーケンス番号が到着順に記録される。

標本期間は、2008年1月2日から2013年12月31日までの1,490営業日である⁸。各日について、S&P 500の構成銘柄のほとんどが取引されているニューヨーク証券取引所の通常取引時間に対応して、シカゴ時間の8:30から15:00までの観測値を抽出した。以下では、標本に十分な観測値が含まれるように、最も活発な（一日の取引量が最も多い）限月に分析対象を限定する⁹。

2.1  変数と基本統計量

BBOデータから、中値リターンr_tを1秒ごとに計測し、Cont et al.（2014）が提案する方法で次のようにOFIを計算する。$P_n^a$と$q_n^a$をベスト・アスクの価格とサイズのn番目の観測値、$P_n^b$と$q_n^b$をベスト・ビッドの価格とサイズのn番目の観測値とし、オーダー・ブック・イベントを次のように定義する。

  

$$e_n=q_n^b{I}_{\{P_n^b\ge P_{n-1}^b\}}-q_{n-1}^b{I}_{\{P_n^b\le P_{n-1}^b\}}-q_n^a{I}_{\{P_n^a\le P_{n-1}^a\}}+q_{n-1}^a{I}_{\{P_n^a\ge P_{n-1}^a\}}$$

ここで、I_{A}はイベントAの指示関数を表す。各1秒区間でe_nを足し合わせOFIを計算する。以下では、OFIをf_tと表記する¹⁰。オーダー・ブック・イベントe_nは、成行注文、指値注文、キャンセルによって引き起こされるベスト・ビッドとベスト・アスクにおける注文板の変化を表していることから、f_tはベスト・ビッドとベスト・アスクにおける需要と供給の不均衡を表すと考えられる。

また、市場の状態を表す変数（以下では市場変数と呼ぶ）も計算する。オーダー・ブック・イベントの数とイベントの平均サイズはそれぞれ注文の活発さと積極性を反映し、平均スプレッドは取引コストを表す。市場の流動性の1側面を示すデプスは、Cont et al.（2014）によって提示された単純化LOBモデルにおける定義に従い、価格変化の前後におけるベスト・ビッドとベスト・アスクのサイズを平均することによって次のように推定する。

  

$$D_t=\frac{1}{2}\left[\frac{\sum _{n\in I_t}\left(q_n^b{I}_{\{P_n^b<P_{n-1}^b\}}+q_{n-1}^b{I}_{\{P_n^b>P_{n-1}^b\}}\right)}{\sum _{n\in I_t}{I}_{\{P_n^b\ne P_{n-1}^b\}}}\right.$$

  

$$+\left.\frac{\sum _{n\in I_i}\left(q_n^a{I}_{\{P_n^a>P_{n-1}^a\}}+q_{n-1}^a{I}_{\{P_n^a<P_{n-1}^a\}}\right)}{\sum _{n\in I_t}{I}_{\{P_n^a\ne P_{n-1}^a\}}}\right]$$（1）

ただし、I_tは変数が計算される1秒区間を表す。

表1には、上記の変数の基本統計量が計算されている。中値リターンとOFIはゼロを中心にほぼ対称で、平均値に比べて標準偏差が大きい。OFIのパーセンタイルからは、ビッドまたはアスクの片側に注文が集中する区間があることが示唆される。市場変数については、平均して45のイベントが発生し、イベントの平均サイズは15である。全1秒区間の5％以上（1,725,000区間以上）で、50以上のサイズで数百件の注文またはキャンセルが発生している。これらの変数の大きな変動に反して、平均スプレッドは最小ティックサイズの0.25とほぼ同じである。また、イベントの平均サイズに比べてデプスは大きい。したがって、S&P 500 E-mini先物市場は流動性が高く活発であることが示唆される。そのため、1秒以内に複数のイベントが発生し、計算された中値リターンとOFIに内生性が生じる可能性がある。内生性がプライス・インパクトの推定に及ぼす影響については、第3節で詳しく説明する。

表1 中値リターンとOFIおよび市場変数の基本統計量

	平均	SD	1％	5％	25％	50％	75％	95％	99％
中値リターン	0.00	0.91	−2.86	−1.78	0.00	0.00	0.00	1.78	2.87
OFI	−0.00	0.52	−1.60	−0.48	−0.03	0.00	0.03	0.47	1.59
イベント数	0.45	0.66	0.01	0.03	0.10	0.23	0.51	1.72	3.27
平均サイズ	0.15	0.36	0.01	0.01	0.03	0.06	0.13	0.59	1.43
平均スプレッド	0.25	0.01	0.25	0.25	0.25	0.25	0.25	0.26	0.30
デプス	0.63	0.43	0.07	0.12	0.33	0.55	0.84	1.43	2.05

（注）リターン、OFI、イベントの数と平均サイズ、平均スプレッドは1秒区間で計算された34,512,298個の標本から、デプスは1秒区間で計算された5,874,016個の標本から計算された統計量を表す。SDは標準偏差を表す。リターンはベーシス・ポイント（10,000倍）、OFIとデプスは1,000倍、イベントの数と平均サイズは100倍した数値を示している。

（出所）筆者作成。

2.2  日内変動

図1は、リターンの標準偏差とOFIの日内変動、および市場変数の平均値を示したものである。この2つの系列の標準偏差、およびイベントの数と平均サイズの平均値は、ほぼU字型のパターンを示しており、市場の寄り付き後と大引け前に活発で（価格変化を伴うような）積極的な注文が出されていることを示唆している。このような現象は、多くの先行研究で観察されている（脚注4参照）。

図1 中値リターンとOFIの標準偏差、および、イベント数の平均値、イベントの平均サイズ、平均スプレッド、デプスの平均値の日内変動

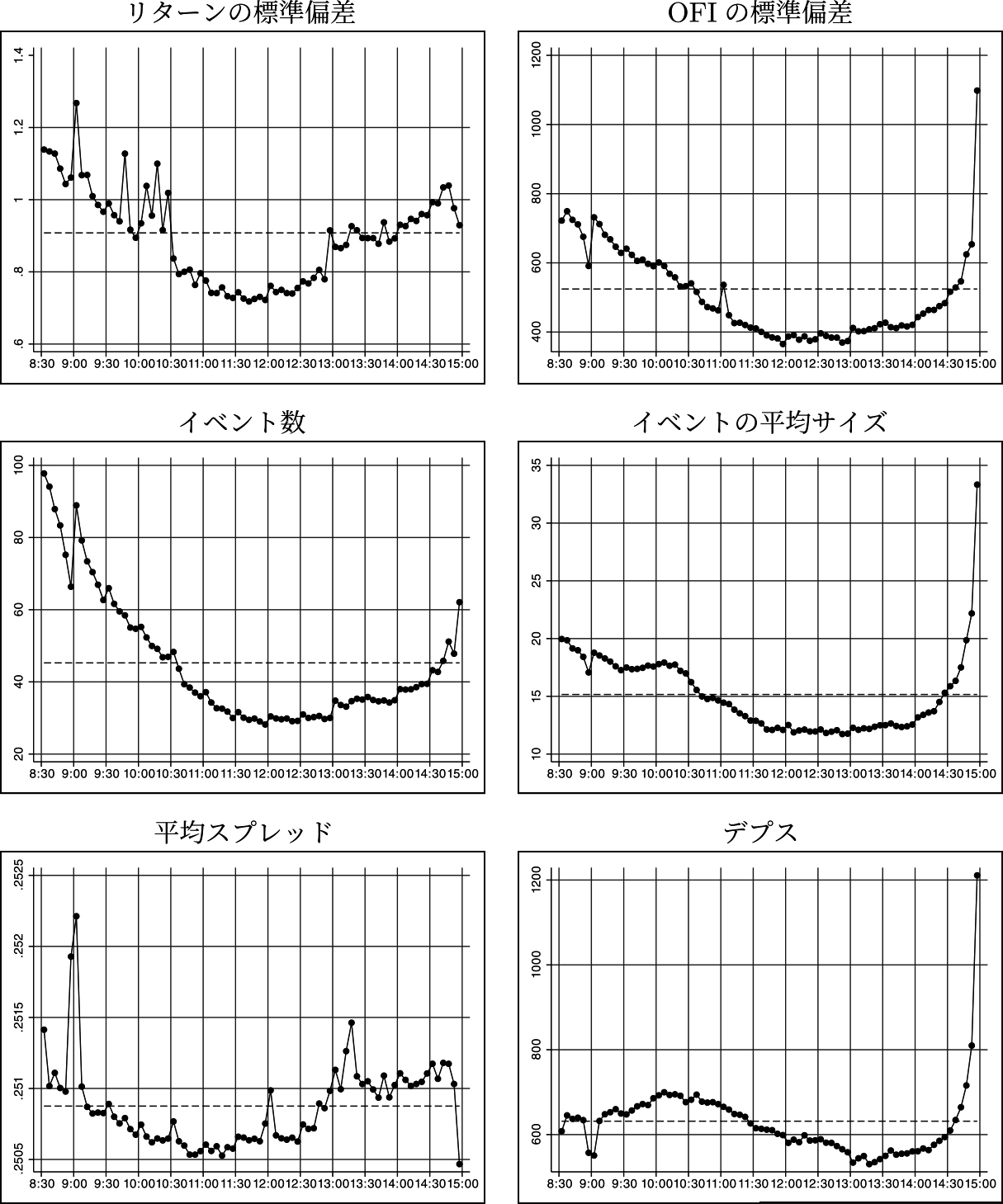
（注）8:30から15:00までの5分区間ごとに計算した値を表す。破線はすべての標本から計算した値を示す。

（出所）筆者作成。

注目すべきは、最後の5分間14:55～15:00において、OFIの標準偏差、イベントの平均サイズの平均値、デプスの平均値が大きく上昇しているのに対し、リターンの標準偏差と平均スプレッドの平均値は低下していることである。これは、ビッドとアスクの片側にはより頻繁でより大きな注文があるものの、大引け前の市場は流動性が高いため、リターンは変動しにくいことを示唆している。また、9時前後に、リターンの標準偏差と平均スプレッドの平均値が急上昇するのに対し、他の4つの系列は低下している。これは、この時間帯の市場は流動性が低く、市場参加者が注文を出すのを控えていることを示唆している。

3.  モデルと推定方法

本節では、リターンとOFIの間の相互作用を分析するために、Deuskar and Johnson（2011）に基づいたモデルとその推定方法について説明する。まず、単純な2変量モデルを導入し、内生性の問題を説明する。次に、簡単な設定の下、ITHを利用した推定手法を説明する。さらに、リターンとOFIの間の内生性と動的相互作用を考慮したSVARモデルを提示し、瞬間的な影響（瞬時インパクト）と長期的な影響（ロングラン・インパクト）を定義する。最後に、SVARモデルが完全に識別されたことを所与として、OFIのショックによるリスクの割合を示すフロー・ドリブン・リスク（flow driven risk：FDR）を導入する。

3.1  2変量モデル

OFI f_tから同時点のリターンr_tへの影響は以下の式で表される。

  

$$r_t=b_r{f}_t+{ϵ}_{r,t},\hspace{1em}{ϵ}_{r,t}\sim (0,{\omega }_r^2)$$（2）

ここで、ϵ_r,tは平均ゼロ、分散${\omega }_r^2$のリターンの撹乱項である。係数b_rはプライス・インパクトで、OFIのリターンへの影響を反映する。つまり、b_rは市場の非流動性を表し、b_rの値が大きいほど市場の流動性が低いことを示す。したがって、市場が完全に流動的な場合、b_rはゼロとなる。

最も高い頻度では、1つの注文のプライス・インパクトは、LOBの形状に応じた機械的な価格変化となる。具体的には、Cont et al.（2014）が導入した単純化LOBモデルの下で、Dを市場のデプスとすると、プライス・インパクトは近似的に1/2Dとなる。Cont et al.（2014）は、ニューヨーク証券取引所の取引・気配データを用いてOFIを計算し、OFIのプライス・インパクトは単純化LOBモデルが示唆するものに近いことを示した。

しかし、リターンとOFIは、通常、複数の注文を含む区間で計算される。そのため、必然的に内生性が発生する（リターンが区間内の追加注文を誘発する）可能性がある¹¹。Deuskar and Johnson（2011）は、内生性を考慮して、リターン方程式（2）に加えて、リターンがOFIに与える影響を次のように定式化した。

  

$$f_t=b_f{r}_t+{ϵ}_{f,t},\hspace{1em}{ϵ}_{f,t}\sim (0,{\omega }_f^2)$$（3）

ここで、ϵ_f,tは平均ゼロ、分散${\omega }_f^2$のOFIの撹乱項であり、任意のsについてϵ_r,sと無相関であると仮定される。係数b_fは、リターンが同区間のOFIに与える影響を表し、以下ではフロー・インパクトと呼ぶ。フロー・インパクトb_fは、内生性の強さを表しており、内生性がない場合はゼロとなる。

リターン方程式（2）とフロー方程式（3）は、以下の2変量モデルとしてまとめられる。

  

$$B{y}_t={ϵ}_t,\hspace{1em}{ϵ}_t\sim (0,\mathrm{\Omega })$$（4）

ただし、y_t=(r_t, f_t)'、ϵ_t=(ϵ_r,t, ϵ_f,t)'とし、行列BとΩは次のように定義される。

  

$$B=\left(\begin{array}{cc}1& -b_r\\ -b_f& 1\end{array}\right),\hspace{1em}\mathrm{\Omega }=\left(\begin{array}{cc}{\omega }_r^2& 0\\ 0& {\omega }_f^2\end{array}\right)$$（5）

この2変量モデルは、次のように書き換えることができる。

  

$$r_t=\frac{1}{1-b_r{b}_f}{ϵ}_{r,t}+\frac{b_r}{1-b_r{b}_f}{ϵ}_{f,t},\hspace{1em}{ϵ}_{r,t}\sim N(0,{\omega }_r^2),$$

  

$$f_t=\frac{b_f}{1-b_r{b}_f}{ϵ}_{r,t}+\frac{1}{1-b_r{b}_f}{ϵ}_{f,t},\hspace{1em}{ϵ}_{f,t}\sim N(0,{\omega }_f^2)$$

f_tとϵ_r,tは明らかに相関しており、リターン方程式（2）のb_rの最小2乗推定量${\widehat{b}}_r$は以下に示すように一致推定量とはならない。

  

$${\widehat{b}}_r-b_r ⟶ \frac{\mathrm{Cov}(f_t,{ϵ}_{r,t})}{\mathrm{Var}\left(f_t\right)}=\frac{(1-b_r{b}_f)b_f{\omega }_r^2}{b_f^2{\omega }_r^2+{\omega }_f^2}={\delta }_{br}$$（6）

ここで、δ_brは${\widehat{b}}_r$の漸近バイアスを表す。このように、内生性が存在する場合、つまりb_f≠0の場合、OLSを用いてb_rを一致推定することはできないため、次節で説明するITHを用いてパラメータを推定する。

3.2  ITH

y_tの分散共分散行列Σを次のように定義する。

  

$$\mathrm{\Sigma }=\mathrm{Var}(y_t)=\left(\begin{array}{cc}{\sigma }_r^2& {\sigma }_{rf}\\ {\sigma }_{rf}& {\sigma }_f^2\end{array}\right)$$（7）

（4）の両辺の分散を取ると、BΣB'=Ωとなり、次の3つの式が得られる。

  

$${\sigma }_r^2-2b_r{\sigma }_{rf}+b_r^2{\sigma }_f^2-{\omega }_r^2=0$$（8）

  

$${\sigma }_f^2-2b_f{\sigma }_{rf}+b_f^2{\sigma }_r^2-{\omega }_f^2=0$$（9）

  

$$b_f{\sigma }_r^2-(1+b_r{b}_f){\sigma }_{rf}+b_r{\sigma }_f^2=0$$（10）

分散${\sigma }_r^2$と${\sigma }_f^2$および共分散σ_rfは、y_tの標本分散と標本共分散として推定できる。したがって、この3つの式には4つの未知パラメータ（b_r, b_f, ω_r, ω_f）があり、追加の制約なしにはパラメータを識別できない。

この識別問題を解決するために、ITHでは、（7）で与えられる分散共分散行列Σの不均一性を利用する。分散${\sigma }_r^2$と${\sigma }_f^2$および共分散σ_rfが変化する一方で、行列Bのプライス・インパクトb_rおよびフロー・インパクトb_fが変わらない状態がS個あるとする。すなわち、各状態s=1, 2, ..., Sについて分散共分散方程式（8）、（9）、（10）があり、b_rとb_fは各状態で同じままであるが、ω_r,sとω_f,sはsによって異なる。

この場合、3S個の式に2+2S個のパラメータが存在することになる。状態s=1, 2, ..., Sについての${\sigma }_r^2$、${\sigma }_f^2$、σ_rfの推定値を${\sigma }_{r,s}^2$、${\sigma }_{f,s}^2$、σ_rf,sとすると、パラメータが識別されるための条件は次のようになる¹²。

オーダー条件：S≥2

ランク条件：任意のペアs'≠s"について　${\sigma }_{r,s^{\mathrm{\text{'}}}}^2{\sigma }_{rf,s^{\mathrm{\text{'}}\mathrm{\text{'}}}}-{\sigma }_{r,s^{\mathrm{\text{'}}\mathrm{\text{'}}}}^2{\sigma }_{rf,s^{\mathrm{\text{'}}}}\ne 0$　（11）

具体的には、オーダー条件とランク条件が満たされている場合、S個の状態の分散共分散方程式（8）–（10）から得られる3S個のモーメント条件を利用して、一般化モーメント法（generalized method of moments：GMM）によってパラメータを推定することができる。

Deuskar and Johnson（2011）は、b_rとb_fがサンプル期間中一定であるのに対し、分散${\omega }_r^2$と${\omega }_f^2$は1日または数日で変化すると仮定して、2変量モデルを推定した。彼らは、b_rとb_fがともに有意に正であること、つまり、OFIに有意な内生性があり、それがプライス・インパクトの同時性バイアスの原因になっていることを示した¹³。

3.3  SVARモデル

2変量モデル（4）はOFIの内生性を考慮しているが、リターンとOFIの系列相関を無視している。リターンとOFIの間の内生性と系列相関の両方を考慮したSVARモデルは次のようになる。

  

$$B{y}_t=c+{\mathrm{\Phi }}_1{y}_{t-1}+{\mathrm{\Phi }}_2{y}_{t-2}+\cdots +{\mathrm{\Phi }}_p{y}_{t-p}+{ϵ}_t,\hspace{1em}{ϵ}_t\sim (0,\mathrm{\Omega })$$（12）

ここで、BとΩは（5）で定義された行列で、Φ_jは自己相関を捉える2×2行列である。

SVARモデル（12）は、次のような誘導型VARモデルとして書くことができる。

  

$$y_t=\tilde{c}+{\tilde{\mathrm{\Phi }}}_1{y}_{t-1}+{\tilde{\mathrm{\Phi }}}_2{y}_{t-2}+\cdots +{\tilde{\mathrm{\Phi }}}_p{y}_{t-p}+{\eta }_t$$（13）

ただし、

  

$$\tilde{c}=B^{-1}c,\hspace{1em}{\tilde{\mathrm{\Phi }}}_j=B^{-1}{\mathrm{\Phi }}_j (j=\mathrm{1,2},\dots ,p),\hspace{1em}{\eta }_t=B^{-1}{ϵ}_t$$

である。

Bη_t=ϵ_tの両辺の分散を取ると、再び分散共分散方程式（8）–（10）を得る。したがって、SVARモデルは2段階で推定することができる。まず、誘導型VARモデル（13）を推定する。次に、残差${\widehat{\eta }}_t$にITHを適用して、プライス・インパクトb_rとフロー・インパクトb_fおよび標準偏差ω_rとω_fを推定する。

SVARモデルが完全に識別されると、リターンとOFIの撹乱項に対するインパルス応答関数を通常の方法で計算できる。IRF_ij(k)をk次のラグにおけるjの撹乱項1単位のショックに対するiの応答とする。ただし、i,j∈{1,2}={r,f}である。例えば、IRF₁₂(k)またはIRF_rf(k)は、ラグkのプライス・インパクトである。累積インパルス応答は次のように計算される。

  

$$I_{ij}(K)=\sum _{k=0}^{K}IR{F}_{ij}(k)$$

以下では、ラグk=0のインパルス応答I_ij(0)=IRF_ij(0)を瞬時インパクトと呼ぶ。また、ロングラン・インパクトは次のように定義される。

  

$$I_{ij}(\infty )=\sum _{k=0}^{\infty }IR{F}_{ij}(k)={\left[(I_2-{\tilde{\mathrm{\Phi }}}_1-{\tilde{\mathrm{\Phi }}}_2-\cdots -{\tilde{\mathrm{\Phi }}}_p{)}^{-1}{B}^{-1}\right]}_{ij}$$（14）

ここで、I₂は2×2の単位行列、[A]_ijは行列Aの（i, j）要素を表す。

3.4  FDR

パラメータが識別されると、誘導型VARモデルのリターンの残差η_r,tを、次のように表すことができる。

  

$${\eta }_{r,t}=\frac{1}{1-b_r{b}_f}{ϵ}_{r,t}+\frac{b_r}{1-b_r{b}_f}{ϵ}_{f,t}$$

ここで、1/(1−b_rb_f)とb_r/(1−b_rb_f)は、直交する撹乱項ϵ_rとϵ_fの1単位のショックの影響を示しており、それぞれ瞬時インパクトI_rr(0)とI_rf(0)に対応する。また、過去のリターンとOFIを条件としたリターンの分散は次のように計算される。

  

$${\tau }^2=\mathrm{Var}[{\eta }_{r,t}]={\tau }_r^2+{\tau }_f^2,\hspace{1em}{\tau }_r^2=\frac{{\omega }_r^2}{(1-b_r{b}_f{)}^2},\hspace{1em}{\tau }_f^2=\frac{b_r^2{\omega }_f^2}{(1-b_r{b}_f{)}^2}$$（15）

ここで、${\tau }_r^2$と${\tau }_f^2$は、リターンとOFIの撹乱項ϵ_rとϵ_fへのショック（以下では、それぞれリターン・ショックとフロー・ショックと呼ぶ）による条件付き分散である。

Deuskar and Johnson（2011）は、FDRをフロー・ショックによる条件付き分散の全分散に対する比率として次のように定義している。

  

$$\mathrm{FDR}=\frac{{\tau }_f^2}{{\tau }_r^2+{\tau }_f^2}=\frac{b_r^2{\omega }_f^2}{{\omega }_r^2+b_r^2{\omega }_f^2}$$（16）

FDRは、${\omega }_f^2$で重み付けされたプライス・インパクトによるリスク$b_r^2{\omega }_f^2$がリスク全体に占める割合を表す。${\omega }_r^2$が固定されている場合、プライス・インパクトb_fが高いか、フローの標準偏差${\omega }_f^2$がより高いか、あるいはその両方である場合に、FDRは大きくなる。したがって、FDRはOFIがどれだけ価格変化に寄与するか、すなわち価格についての情報量を反映する変量である。

4.  推定結果

本節では、SVARモデル（12）の推定結果と関連する分析結果を示す。まず、誘導型VARモデル（13）の推定結果をまとめる。次に、ITHによるパラメータおよび関連する変量の推定結果を示す。さらに、インパルス応答分析を用いて、リターンとOFIの間の動的な相互作用を分析する。

4.1  誘導型VARモデルの推定結果

表2には、1秒区間のリターンr_tとOFI f_tについての誘導型VARモデル（13）を各日の15分区間ごとに計38,740個の区間で推定した結果がまとめられている。赤池情報量規準（Akaike information criterion：AIC）を用いて選択したラグの数pは、38,740個のうち38,725個の区間でゼロより大きかった。

表2 誘導型VARモデル（13）の推定結果

	平均	SD	1％	5％	25％	50％	75％	95％	99％	t+	t−
p	5.568	4.703	1	2	3	4	7	14	26	—	—
${\tilde{\varphi }}_{1,rr}$	−0.312	0.132	−0.604	−0.520	−0.402	−0.314	−0.223	0.091	−0.000	0.00	0.94
${\tilde{\varphi }}_{1,rf}$	0.464	0.541	−0.187	0.018	0.183	0.319	0.548	1.437	2.766	0.83	0.01
${\tilde{\varphi }}_{1,fr}$	0.003	0.095	−0.241	−0.142	−0.045	−0.001	0.048	0.161	0.276	0.22	0.15
${\tilde{\varphi }}_{1,ff}$	0.041	0.177	−0.490	−0.318	−0.038	0.074	0.152	0.276	0.372	0.43	0.18
$R_r^2$	0.087	0.058	0.008	0.019	0.044	0.074	0.119	0.195	0.264	—	—
$R_f^2$	0.046	0.045	0.002	0.006	0.018	0.032	0.057	0.130	0.227	—	—

（注）モデルは38,740個の15分区間それぞれで推定された。AICを用いて選択したラグの数pは、38,725個の区間でゼロより大きかった。${\tilde{\varphi }}_{1,rr}$、${\tilde{\varphi }}_{1,rf}$、${\tilde{\varphi }}_{1,fr}$、${\tilde{\varphi }}_{1,ff}$は、それぞれ${\tilde{\mathrm{\Phi }}}_1$の第（1,1）、（1,2）、（2,1）、（2,2）要素を表す。SDは標準偏差を表す。t⁺は推定値が有意に正（t値が2より大）の割合を示し、t⁻は推定値が有意に負（t値が−2より小）の割合を示す。$R_r^2$と$R_f^2$は、それぞれリターンとOFIについての決定係数である。パラメータの統計量と決定係数は、AICによりp=0が選択された15個の区間を除く38,725個の標本から計算した。

（出所）筆者作成。

リターンについては、1次のラグ・リターンr_t−1の係数${\tilde{\varphi }}_{1,rr}$は、94％の区間で有意に負（t値が−2より小）であり、1秒区間という短時間でもリターン・リバーサル（逆張り現象）が見られた。対照的に、1次のラグOFI f_t−1の係数${\tilde{\varphi }}_{1,rf}$は、83％の区間で有意に正（t値は2より大）であり、OFIのリターンへの影響が数秒間続くことが示唆された。

OFIについては、1次のラグ・リターンr_t−1の係数${\tilde{\varphi }}_{1,fr}$は、22％の区間で有意に正であり、15％の区間で有意に負である。この結果から、リターンが後続のOFIに有意な影響を与えていることが示された。また、1次のラグOFI f_t−1の係数${\tilde{\varphi }}_{1,ff}$は、43％の区間で有意に正であり、18％の区間で有意に負であることから、リターンのOFIへの影響は数秒間続くことが示唆された。つまり、リターンとOFIが数秒の区間で計算される場合には、内生性が存在することが確認された。

リターンとOFIのラグは、平均して、リターンの変動の8.7％を、OFIの変動の4.6％を説明する。また、決定係数の値が20％を超えた区間も1％以上ある。これらの推定結果から、リターンとOFIには有意な系列相関と相互相関があることが確認された。このような相関構造は、ITHを用いて構造パラメータを推定した後、インパルス応答分析によってさらに詳細に検討することができる。

4.2  ITHによる推定結果

誘導型VARモデルの推定から得られた残差を用いてITHにより構造パラメータ（b_r, b_f, ω_r, ω_f）を次のように推定した。まず、残差の分散と共分散を各日の各5分区間で計算した。次に、38,740個の15分区間について、3つの状態のすべてのペアについて、ランク条件（11）を満たすか検証した。最後に、ランク条件を満たした37,029個の15分区間それぞれについて、残差${\widehat{\eta }}_t$にITHを利用したGMMにより構造パラメータを推定した。具体的には、プライス・インパクトb_rとフロー・インパクトb_fは正で、各15分区間で固定されていると仮定し、標準偏差ω_rとω_fは15分区間の3つの5分区間で変化すると仮定した。すなわち、15分区間ごとに1組の（b_r, b_f）と3組の（ω_r, ω_f）を推定した。すべての組み合わせでランク条件を満たす状態が3つあるので、GMMのモーメント条件は9個であり過剰識別となる。

ITHによる推定結果が表3にまとめられている。プライス・インパクトb_rはほぼゼロ（0.0005より小さい）から5近くまで大きく変動し、64％の区間で統計的に有意であった。平均値は0.834で、8:30から15:00までの1分区間のリターンとOFIを用いたDeuskar and Johnson（2011）の結果から示唆される条件付きプライス・インパクトの平均値0.474の1.76倍である¹⁴。この結果は、リターンやOFIの測定間隔が短くなると、プライス・インパクトが上昇することを示唆している¹⁵。

表3 ITHによる推定結果

	平均	SD	1％	5％	25％	50％	75％	95％	99％	*
br	0.834	0.999	0.000	0.000	0.242	0.556	1.065	2.576	4.950	0.64
bf	0.301	0.242	0.000	0.000	0.133	0.246	0.419	0.772	1.088	0.71
ωr,1	0.574	0.408	0.123	0.198	0.335	0.475	0.682	1.282	2.135	0.98
ωr,2	0.554	0.382	0.121	0.191	0.326	0.463	0.659	1.227	2.049	0.98
ωr,3	0.552	0.393	0.122	0.192	0.324	0.459	0.654	1.227	2.069	0.98
ωf,1	0.344	0.242	0.068	0.105	0.188	0.280	0.424	0.814	1.223	0.96
ωf,2	0.339	0.234	0.068	0.104	0.186	0.278	0.419	0.788	1.228	0.96
ωf,3	0.344	0.245	0.066	0.102	0.185	0.278	0.425	0.814	1.252	0.96
J	1.098	1.409	0.000	0.006	0.146	0.575	1.516	3.977	6.432	0.99
${\widehat{b}}_r$	1.529	1.566	0.197	0.291	0.569	1.0052	1.902	4.393	8.372	1.00
${\widehat{b}}_r$−br	0.695	0.940	−0.072	−0.013	0.173	0.408	0.865	2.326	4.673	—
δbr	0.732	0.962	0.000	0.000	0.192	0.438	0.906	2.398	4.808	—
${\tau }_r^2$	0.644	1.737	0.019	0.049	0.140	0.286	0.609	2.211	6.132	—
${\tau }_f^2$	0.125	0.361	0.000	0.000	0.008	0.036	0.112	0.495	1.404	—
FDR	0.176	0.187	0.000	0.000	0.027	0.109	0.274	0.576	0.740	—

（注）ランク条件（11）を満たす15分区間それぞれについて、プライス・インパクトとフロー・インパクト（b_r, b_f）と3組の標準偏差（ω_r,1, ω_r,2, ω_r,3, ω_f,1, ω_f,2, ω_f,3）を推定した。JはHansen（1982）の過剰識別検定のJ統計量である。${\widehat{b}}_r$はb_rのOLS推定値を表し、δ_brは（6）で定義された${\widehat{b}}_r$の漸近バイアスである。また、${\tau }_r^2$と${\tau }_f^2$は（15）で定義されたリターンとOFIの条件付き分散を表し、$FDR={\tau }_f^2/({\tau }_r^2+{\tau }_f^2)$である。b_rとb_fの統計量は37,029個の推定値から、その他の統計量は116,220個の推定値から計算した。SDは標準偏差を表す。最後の列＊はパラメータの推定値については係数が有意（t値の絶対値が2より大）の区間の割合を示し、J統計量については有意水準5％で棄却されなかった区間の割合を表す。

（出所）筆者作成。

対照的に、フロー・インパクトb_fの変化は緩やかで、ほとんどの区間で0から1の間である。また、71％の区間で統計的に有意であり、1秒区間でも内生性が確認された。平均値は0.301で、Deuskar and Johnson（2011）で報告された推定値0.55の約0.55倍である。この結果は、時間間隔が短くなるとb_fが減少することを示唆しており、リターンとOFIがイベントごとに計算される場合には内生性が存在しないことと整合的である。

標準偏差ω_rとω_fは、96％以上の区間で統計的に有意であり、大きな変動を示した。統計量は3つの5分区間で類似しているが、ランク条件（11）は満たしており、有意水準5％でのHansen（1982）の過剰識別検定は99％の区間で棄却されない。また、表1に示したリターンとOFIの標準偏差と同様に、すべての5分区間でω_rの平均値はω_fの平均値よりも高い。

表3には、OLS推定値${\widehat{b}}_r$、OLS推定値とITH推定値の差${\widehat{b}}_r$−b_r、および（6）で定義された漸近バイアスδ_brの統計量も示されている。${\widehat{b}}_r$はITH推定値よりも有意に大きく、OLS推定値には内生性による上方バイアスがあることが確認された。また、${\widehat{b}}_r$はITH推定値より大きな標準偏差を示した。これらの結果は、Deuskar and Johnson（2011）の結果と整合的である。

構造パラメータ（b_r, b_f, ω_r, ω_f）の推定値から、（15）で定義された条件付き分散${\tau }_r^2$と${\tau }_f^2$、および（16）で定義されたFDRを5分区間ごとに計算し、表3にそれらの統計量を示した。${\tau }_r^2$と${\tau }_f^2$はどちらも大きな変動を示したが、${\tau }_f^2$は5％以上の区間でほぼゼロとなっており、トレーダーが注文を控えた期間があることが示唆された。FDRは、平均して全リスク（過去のリターンとOFIを条件としたリターンの条件付き分散）の17.6％を占めた。これは、Deuskar and Johnson（2011）が報告した無条件のプライス・インパクトから計算されたFDRの値0.12–0.13よりもわずかに大きい。また、75％以上の区間で0.3未満であるものの、ほぼゼロから0.74まで大きく変動しており、Deuskar and Johnson（2011）で観測されたFDRの範囲0.41–0.72も含まれている。この結果から、OFIが価格変化に大きく寄与した（価格についての情報量が多い）区間があることが示唆された。

4.3  インパルス応答

各日の15分区間ごとに、リターン・ショックとフロー・ショックによって引き起こされるインパルス応答を計算した。図2には、10次のラグまでのインパルス応答の37,029個の推定値の中央値と、その5％点から95％点の範囲が示されている。1次のラグ以降のインパルス応答はすべて無視できるほど小さく、ショックの影響はほとんど1秒以内に消えていることが示唆された。このようなショックに対する迅速な調整は、ビッドまたはアスクが（表1で示した1秒区間の平均イベント数の半分以下である）約20イベント後に新しいレベルに達することを示したHautsch and Huang（2012）の結果と整合的である。

図2 1単位のリターン・ショックまたはフロー・ショックによるインパルス応答

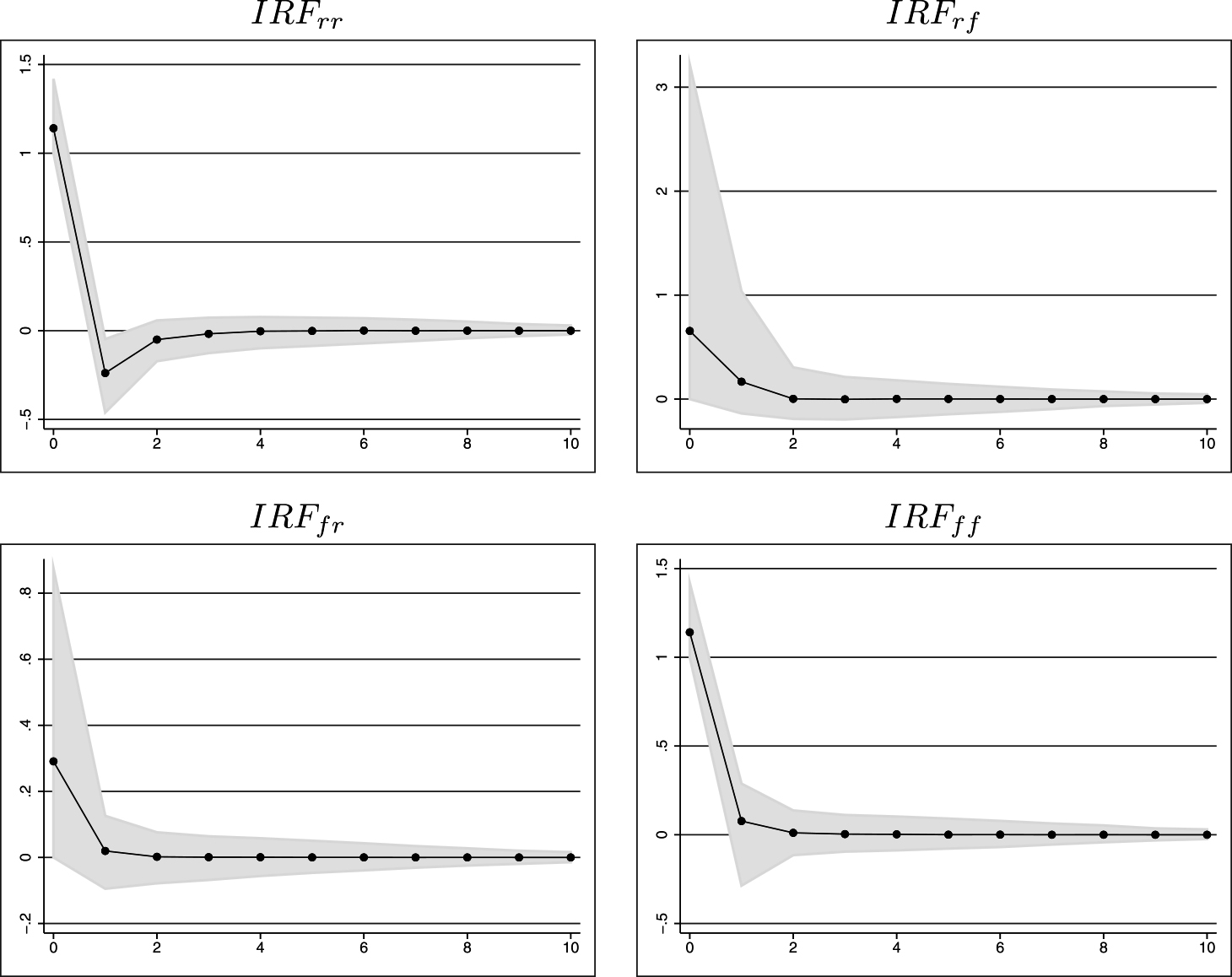
（注）IRF_ijはjへのショックに対するiの応答を表す。例えば、IRF_rfはフロー・ショックによるリターンの変化を表す。黒点は37,029個の推定値の中央値を示し、灰色の領域は5％点から95％点の範囲を表す。

（出所）筆者作成。

表4には、ラグ0と1でのインパルス応答と、（14）で定義されたロングラン・インパクトの基本統計量が示されている。瞬時インパクトIRF_ij(0)はほとんどが正であり、1単位のリターン・ショックおよびフロー・ショックの同じ1秒区間における瞬間的な影響が大きいことが確認された。リターン・ショックによる1次ラグのインパルス応答IRF_rr(1)は95％以上が負であり、表2の誘導型VARモデルの推定結果で観察されたリターン・リバーサルと整合的である。1次ラグの他のインパルス応答は、ゼロ付近で変化しており、符号は明確に決定されない。

表4 37,029個のインパルス応答の推定値の基本統計量

	平均	SD	1％	5％	25％	50％	75％	95％	99％
IRFrr(0)	1.165	0.139	1.000	1.000	1.051	1.141	1.259	1.419	1.545
IRFrr(1)	−0.245	0.129	−0.558	−0.461	−0.328	−0.239	−0.157	−0.047	0.036
Irr(∞)	0.843	0.283	0.338	0.499	0.702	0.834	0.980	1.220	1.399
IRFrf(0)	1.022	1.263	0.000	0.000	0.268	0.655	1.317	3.218	6.329
IRFrf(1)	0.270	0.475	−0.391	−0.138	0.049	0.167	0.342	1.037	2.301
Irf(∞)	1.423	16.688	0.038	0.180	0.454	0.817	1.580	4.122	8.464
IRFfr(0)	0.349	0.275	0.000	0.000	0.161	0.291	0.487	0.875	1.242
IRFfr(1)	0.018	0.071	−0.177	−0.095	−0.015	0.020	0.053	0.126	0.218
Ifr(∞)	0.372	0.721	−0.212	−0.037	0.171	0.320	0.523	0.977	1.455
IRFff(0)	1.165	0.139	1.000	1.000	1.051	1.141	1.259	1.419	1.545
IRFff(1)	0.052	0.169	−0.470	−0.287	−0.019	0.077	0.151	0.288	0.398
Iff(∞)	1.304	6.925	0.514	0.735	1.056	1.224	1.448	1.861	2.226

（注）IRF_ijはjへのショックに対するiの応答を表す。例えば、IRF_rfはフロー・ショックによるリターンの変化を表す。I_ij(∞)は（14）で定義されたロングラン・インパクトを表す。SDは標準偏差を表す。

（出所）筆者作成。

ロングラン・インパクトは、I_fr(∞)のわずかな割合を除いてすべて正である。平均して、1単位のフロー・ショックは、1秒間にビッドまたはアスクのどちらかで1,000件の注文が予想外に増加することに対応し、同じ1秒区間での応答IRF_rf (0)が1.022ベーシス・ポイント、ロングラン・インパクトI_rf (∞)は1.423ベーシス・ポイント、リターンを増加させることが示された。表3のITHによる推定結果から、OFIの撹乱項の標準偏差ω_fの平均値は0.34で、表1に示されたデプスの平均値の約半分である。したがって、デプスの半分のフロー・ショックがもたらすロングラン・インパクトは、およそ0.48（=0.34×1.423）となる。この値は、Hautsch and Huang（2012）で報告されたデプスの半分の指値注文の永続的なプライス・インパクト0.5–0.6ベーシス・ポイントと同等である。

5.  日内変動と市場変数

本節では、推定されたパラメータと関連する変量の日内変動を示し、その変動の原因のいくつかについて議論する。まず、日内変動を図示し、市場変数との関連を例示する。次に、推定されたパラメータと関連する変量を被説明変数とした回帰によって、変動の要因を検証する。

5.1  日内変動

(1)  誘導型VARモデルのパラメータ

図3には、8:30から15:00までの15分区間ごとの誘導型VARモデル（13）の1次のラグ係数の推定値の平均値が示されている。リターンr_tについて、1次のラグ・リターンr_t−1の係数${\tilde{\varphi }}_{1,rr}$は、8:30～8:45に最小値から始まり、9:00～9:15に急激に上昇した後に低下する。その後11:30まで上昇し、残りの時間は平均値より高い水準で穏やかに変動する。この結果から、リターン・リバーサルが寄り付き後の30分間でより顕著であることが示された。一方、1次のラグOFI f_t−1の係数${\tilde{\varphi }}_{1,rf}$は、10:15まで減少し、その後増加して13:30～13:45にピークを迎える。最後の区間14:45～15:00には大幅に低下しており、大引け前にはr_tに対するf_t−1の影響が小さいことが示唆された。

図3 誘導型VARモデル（13）の1次のラグ係数の推定値の日内変動

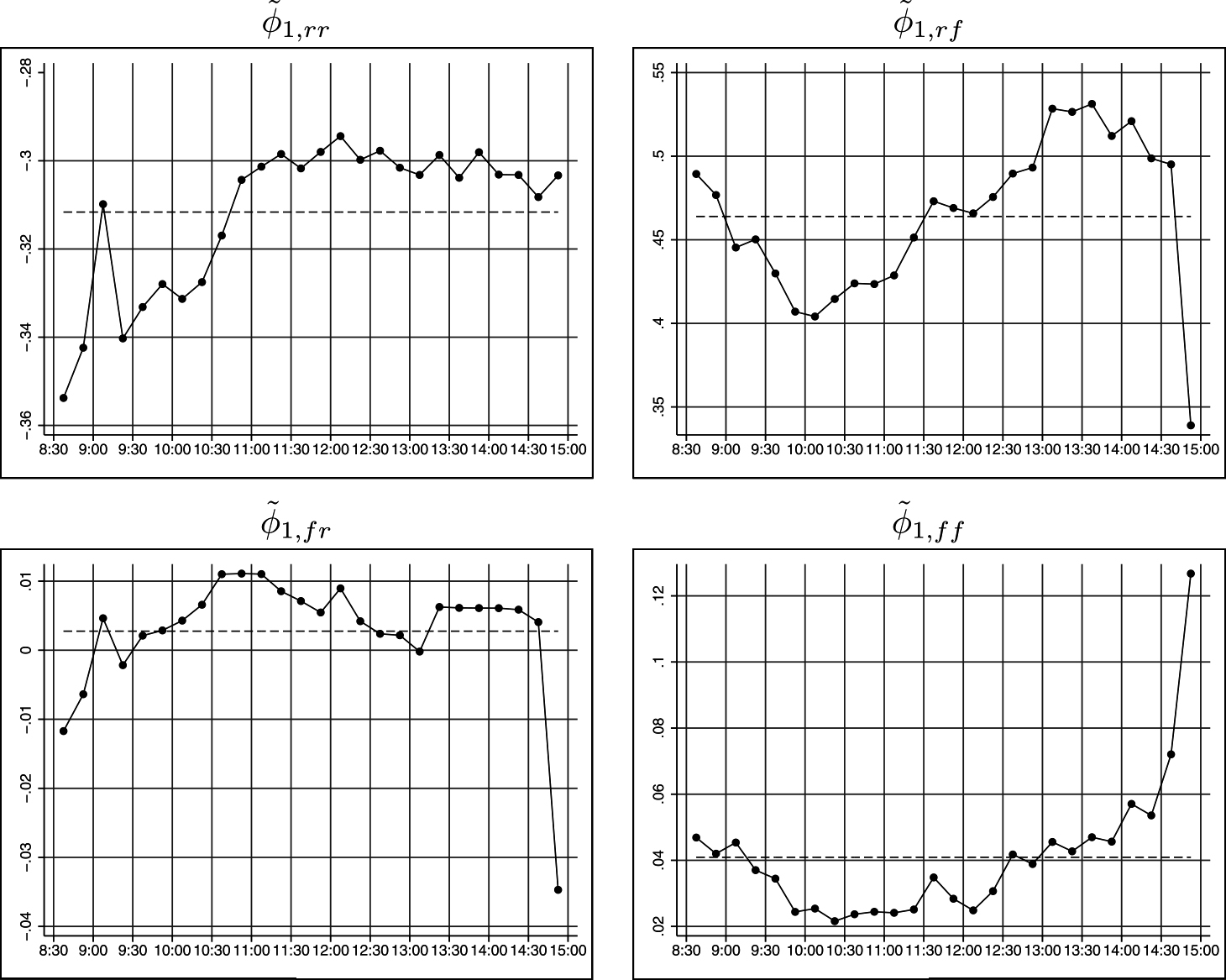
（注）8:30から15:00までの15分区間ごとに38,740個の推定値から計算した平均値を表す。${\tilde{\varphi }}_{1,rr}$、${\tilde{\varphi }}_{1,rf}$、${\tilde{\varphi }}_{1,fr}$、${\tilde{\varphi }}_{1,ff}$は、それぞれ${\tilde{\mathrm{\Phi }}}_1$の第（1,1）、（1,2）、（2,1）、（2,2）要素を示す。破線はすべての標本から計算した平均値を示す。

（出所）筆者作成。

OFIについてのr_t−1の係数${\tilde{\varphi }}_{1,fr}$は、比較的低い値から始まり、14:45まで平均値付近で変動し、その後大幅に低下する。これは、${\tilde{\varphi }}_{1,rf}$と同様に、最後の区間14:45～15:00においてf_tがr_t−1に対してあまり反応しないことを示している。対照的に、f_t−1の係数${\tilde{\varphi }}_{1,ff}$は、14:45～15:00に顕著な増加を伴うJ字型のパターンを示した。この結果は、OFIの自己相関が高く、最後の区間でより多くの持続的（後追い）注文が発生することを示唆しており、図1に示された大引け前に観測される活発で積極的な注文と整合的である。

(2)  構造パラメータ

図4には、8:30から15:00までの15分区間ごとのプライス・インパクトb_rとフロー・インパクトb_fの平均値が示されている。b_rは、8:30～9:15に高い値で始まり、9:15～9:30に低下し、9:45以降に徐々に上昇する。その後、13:00～13:15にピークを迎え、最後の区間14:45～15:00で大幅に低下して最低となる。これは${\tilde{\varphi }}_{1,rf}$と同様の日内変動であり、同区間のOFIと過去のOFIが同じようにリターンに影響を与えていることが示唆された。逆に、b_fは8:45～9:15に増加し、12:00まで徐々に減少する。b_fは12:45～13:00に最低となり、最後の区間で最高値まで急上昇する。これらの結果から、最後の区間14:45～15:00では、リターンはOFIにあまり影響を受けないのに対し、OFIはリターンにより大きく依存することが示唆された。これは、図1で示されたように、大引け前には流動性が高く注文が活発となることと整合的である。

図4 構造パラメータ（b_r, b_f, ω_r, ω_f）の日内変動

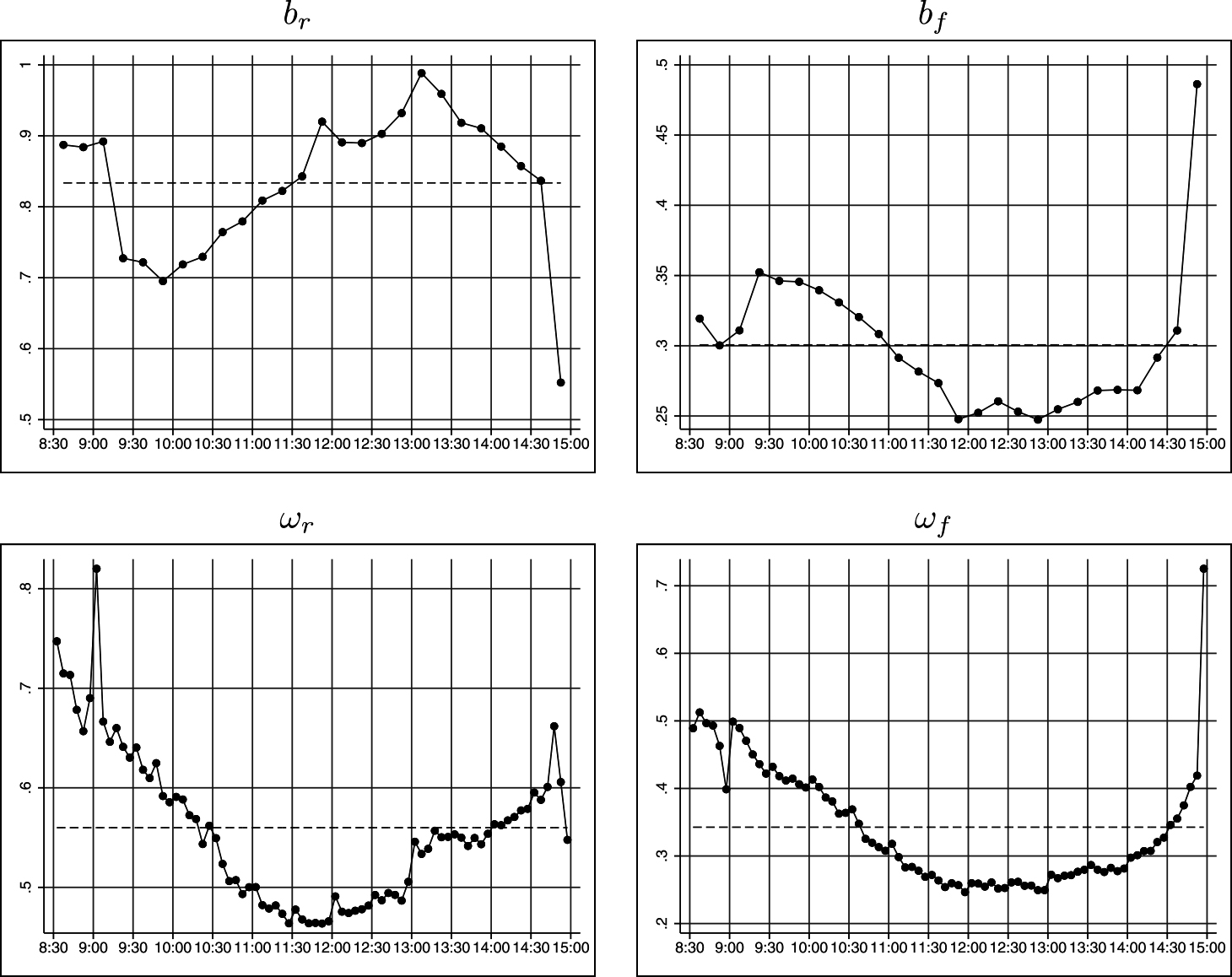
（注）8:30から15:00までの各区間ごとに37,029個の推定値から計算した平均値を表す。プライス・インパクトb_rとフロー・インパクトb_fは15分区間ごとに、標準偏差ω_rとω_fは5分区間ごとに計算した。破線はすべての標本から計算した平均値を示す。

（出所）筆者作成。

図4には、8:30から15:00までの各5分区間のリターンとフローの撹乱項の標準偏差ω_rとω_fの平均値も示されている。概して、ω_rとω_fは、それぞれ図1のリターンとOFIの標準偏差の日内変動を反映している。注目すべきは、最後の5分区間14:55～15:00でω_fが大きく増加していることである。この結果は、図1のOFIの標準偏差とイベントの平均サイズの平均値の急激な上昇と一致しており、この区間での活発で積極的な注文を反映している。また、図1で観察されたように、ω_rは9:00～9:05に急上昇する一方、ω_fは8:55～9:00に低下している。これは、9:00に重要なマクロ経済指標が発表されることと関係していると考えられるが、本稿では扱わない。

(3)  瞬時インパクトとロングラン・インパクト

図5には、各15分区間の瞬時インパクトI_ij(0)とロングラン・インパクトI_ij(∞)の中央値を示した。OFIからリターンへのインパクトであるI_rf(0)とI_rf(∞)は、どちらもプライス・インパクトb_rの日内変動と同様のパターンを示している。一方、フローからリターンへのインパクトであるI_fr(0)とI_fr(∞)は、フローインパクトb_fに似たパターンを示した。したがって、瞬時インパクトとロングラン・インパクトを調べるためには、プライス・インパクトとフロー・インパクトを適切に推定することが重要であることが示唆された。

図5 瞬時インパクトI_ij(0)とロングラン・インパクトI_ij(∞)の日内変動

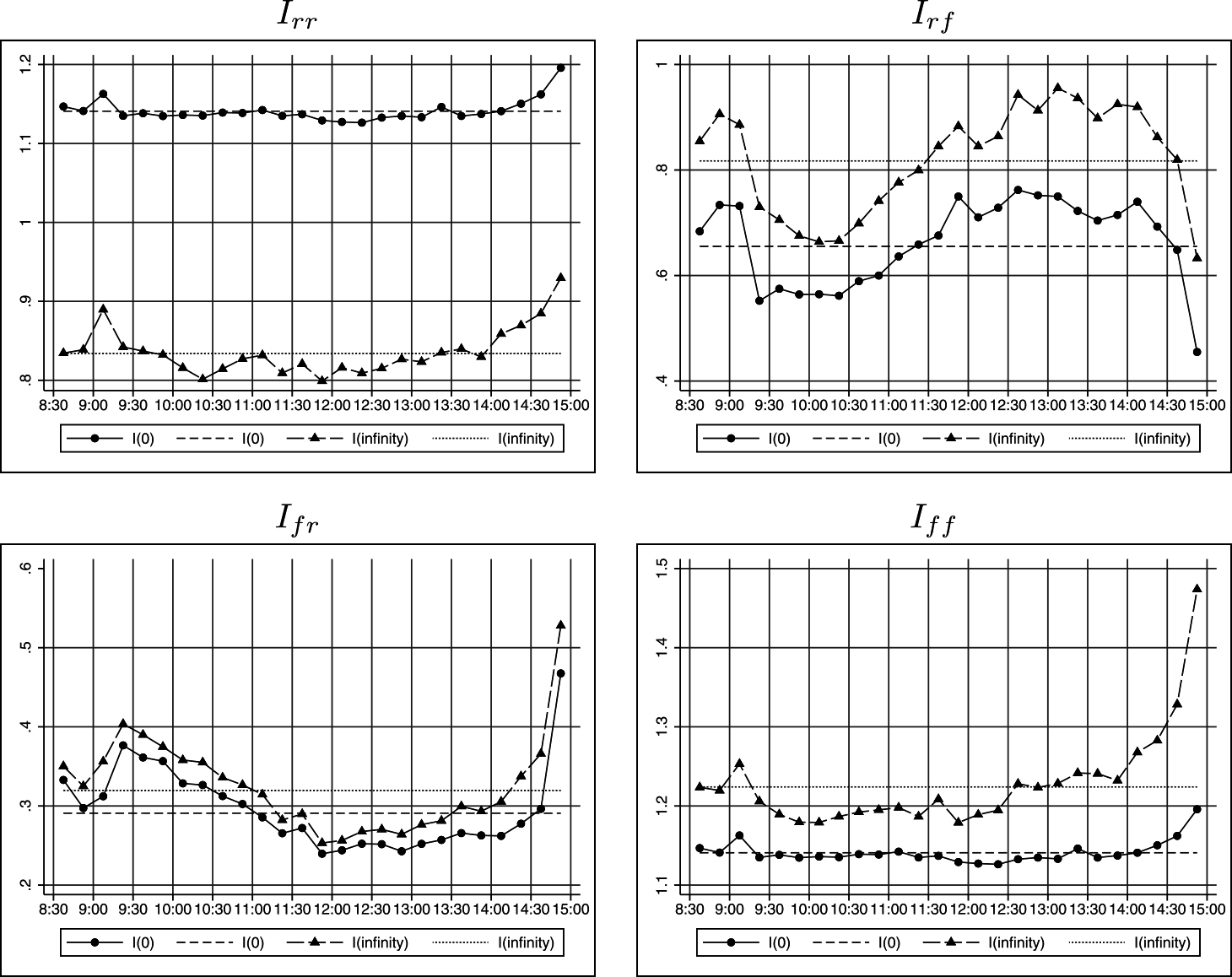
（注）8:30から15:00までの各区間ごとに37,029個の推定値から計算した中央値を表す。I_ijはjへのショックに対するiの応答を表す。例えば、I_rfはフロー・ショックによるリターンの変化を表す。破線はすべての標本から計算した中央値を示す。

（出所）筆者作成。

リターンからリターンへのインパクトであるI_rr(0)とI_rr(∞)は、同様の日内変動を示した。9:00～9:15に急上昇し、最後の数区間で上昇している。瞬時インパクトとロングラン・インパクトの差は、表4で示された有意な負の1次ラグの応答IRF_rr(1)を反映している。フローからフローへのインパクトであるI_ff (0)とI_ff (∞)にも同様の日内変動が観察されたが、瞬時インパクトとロングラン・インパクトの差は、14:45～15:00に大きくなっている。この結果は、フロー・ショックの影響が、特に大引け前の区間に長く続くことを示唆している。これは、図1に示したように、最後の5分区間に観測される活発で積極的な注文を反映している。

(4)  条件付き分散とFDR

図6には、8:30から15:00までの各5分区間の、リターンとOFIの条件付き分散${\tau }_r^2$と${\tau }_f^2$および$FDR={\tau }_f^2/({\tau }_r^2+{\tau }_f^2)$の平均値が示されている。${\tau }_r^2$は、図4に示したω_rと同様の日内変動を示した。一方、τ²_fは独特の日内変動を示し、8:30～9:30に高く、8:55～9:00に大きく低下し、9:30～14:45にほぼU字型に推移した後、14:45～14:50に急落し、14:55～15:00に急上昇した。

図6 リターンとOFIの撹乱項による条件付き分散とFDRの日内変動

（注）8:30から15:00までの各5分区間ごとに37,029個の推定値から計算した平均値を表す。破線はすべての標本から計算した値を示す。

（出所）筆者作成。

FDRについては、14:45～15:00に${\tau }_r^2$と${\tau }_f^2$が逆方向に動くことにより、14:45～14:50に急低下し、14:55～15:00に急上昇している。${\tau }_r^2$の増加と${\tau }_f^2$の大幅な減少を反映して、14:45～14:50にはFDRが10％以下に低下し、その区間ではOFIが価格変化にあまり寄与しないことが示唆された。逆に、${\tau }_r^2$の減少と${\tau }_f^2$の大幅な増加により、FDRは14:55～15:00に25％以上に上昇し、最後の区間ではOFIが価格変化に大きく寄与することが示された。

5.2  変動の要因

図3～6から、推定されたパラメータと関連する変量が日内に大きく変動することが示された。いくつかの日内変動は、デプスやイベント数などの市場変数の変動を反映しているようである。この小節では、推定されたパラメータと関連する変量のそれぞれを市場変数に回帰することで、変動の要因を検証する。

説明変数として、（1）で定義されたデプスの逆数D⁻¹、イベント数NE、イベントの平均サイズASE、平均スプレッドSPRを、被説明変数に応じて5分区間または15分区間で計算した。これらの変数は、市場の状態のいくつかの側面を反映しており、D⁻¹が大きければ市場の流動性は低く、NEが大きければ注文は活発であり、ASEが大きければ積極的な注文が多いことを示し、SPRが大きければ取引コストが高いことになる。以下の回帰分析では、これらの市場変数に加えて、5分区間または15分区間のダミー変数と年のダミー変数を説明変数に用いて、時間効果をコントロールしている。

(1)  15分区間での回帰分析

表5には、15分区間の変数を用いた回帰結果が示されている。プライス・インパクトb_rについては、D⁻¹の係数が有意に正であり、市場の流動性が低い場合にOFIがリターンに及ぼす影響が強くなることが示された。この結果は、Deuskar and Johnson（2011）と整合的であり、彼らの非流動性指標ILOBSが期待プライス・インパクトの良い代理変数であることを示唆する。また、D⁻¹の係数はおよそ0.5で、Cont et al.（2014）の単純化LOBモデルが示唆するプライス・インパクトと整合的である。NEとASEの係数はともに有意に負であり、注文が活発で積極的な場合、OFIが同区間のリターンに与える影響は小さくなることが示された。さらに、SPRが大きくなる（取引コストが上昇する）と、プライス・インパクトb_rが小さくなる。b_rの変動の約54％が、市場変数とダミー変数により説明された。

表5 15分区間での回帰結果

	br	bf	${\widehat{b}}_r$−br	δbr	Irr(0)	Irf(0)	Ifr(0)
D−1	0.553***	−0.066***	0.540***	0.560***	0.002	0.697***	−0.079***
	（0.017）	（0.004）	（0.019）	（0.019）	（0.002）	（0.022）	（0.005）
NE	−1.628***	0.009	−0.536*	−0.591*	0.314***	−1.431***	−0.056
	（0.429）	（0.095）	（0.324）	（0.331）	（0.071）	（0.536）	（0.118）
ASE	−3.421***	1.502***	−3.156***	−3.295***	−1.040***	−5.019***	1.256***
	（0.834）	（0.266）	（0.738）	（0.757）	（0.202）	（1.090）	（0.264）
SPR	−7.510***	3.173***	−3.478*	−3.878**	−2.370***	−12.975***	2.735***
	（2.868）	（0.413）	（1.913）	（1.969）	（0.462）	（4.016）	（0.460）
N	37,029	37,029	37,029	37,029	37,029	37,029	37,029
${\bar{R}}^2$	0.541	0.268	0.571	0.586	0.246	0.542	0.257

（注）第1行は被説明変数を表す。b_rはプライス・インパクト、b_fはフロー・インパクト、${\widehat{b}}_r$−b_rはITH法によるプライス・インパクトの推定値とOLS推定値との差、δ_brは（6）で定義された漸近バイアス、I_ij(0)は瞬時インパクトで、jへのショックに対するiの同区間での応答を表し、I_rr(0)=I_ff(0)=1/(1−b_rb_f)である。第1列は説明変数を表し、単位はデプスの逆数D⁻¹が1000、イベント数NEが100万、イベントの平均サイズASEが1000、平均スプレッドSPRが1である。定数項と15分区間のダミー変数および年のダミー変数は簡潔さのため割愛した。Nは推定に用いたサンプルサイズ、${\bar{R}}^2$は自由度修正済み決定係数を表す。括弧内の数値はロバスト標準誤差であり、*、**、***は、係数がそれぞれ10％、5％、1％の有意水準で有意であることを示す。

（出所）筆者作成。

フロー・インパクトb_fについては、対照的な結果が得られた。D⁻¹とSPRの係数は、それぞれ有意に負と正であり、市場の流動性が低く、取引コストが高い場合にリターンがOFIに与える影響が強くなることが示唆された。NEの係数は有意ではないが、ASEの係数は有意に正であることから、OFIは、積極的な注文が多い場合に、リターンに対してより大きく反応することが示された。決定係数は約27％でb_rの半分程度であり、フロー・インパクトの変動を説明する他の変数の存在が示唆された。

${\widehat{b}}_r$−b_rとδ_brの回帰結果は、どちらもb_rの回帰結果と同様である。すなわち、OLS推定値のバイアスは市場の流動性が低いときに大きくなることが示された。逆に、より活発で積極的な注文があり、取引コストが高い場合には、バイアスは小さくなる。したがって、スプレッドは小さいがデプスが小さいために積極的な注文が少ない場合には、OLS推定値の上方バイアスは大きくなる傾向があるので、プライス・インパクトの推定において内生性を適切に処理することが重要となることが示唆された。

瞬時インパクトI_rf(0)とI_fr(0)は、それぞれb_rとb_fと同様の結果を示した。一方、I_rr(0)=I_ff(0)は、注文が多い場合に増加するが、積極的な注文があり取引コストが高い場合は減少する。I_fr(0)とI_rr(0)=I_ff(0)についての決定係数は25％前後であることから、b_fの結果と同様に、変動を説明する他の要因の存在が示唆された。

(2)  5分区間での回帰分析

表6には、5分区間の変数を用いた回帰結果が示されている。標準偏差ω_rとω_fの結果は、D⁻¹の係数を除いて定性的には同じであった。D⁻¹の係数は、ω_rでは有意に正であるのに対し、ω_fでは有意に負であり、市場の流動性が低い場合には、ω_rが増加し、ω_fが減少することが示された。他の変数の係数は有意に正であり、注文が活発で積極的であり、取引コストが高い場合にω_rとω_fが増加することを示している。これらの変数とダミー変数により、ω_rの変動の約68％が、ω_fの変動の約51％が説明された。条件付き分散${\tau }_r^2$と${\tau }_f^2$についての結果は、決定係数は低いがω_rについての結果と同様である。

表6 5分区間での回帰結果

	ωr	ωf	${\tau }_r^2$	${\tau }_f^2$	FDR
D−1	0.204***	−0.049***	0.783***	0.118***	−0.016***
	（0.007）	（0.002）	（0.070）	（0.009）	（0.002）
NE	12.357***	9.423***	19.273***	6.413***	−0.277
	（0.434）	（0.449）	（2.065）	（0.509）	（0.177）
ASE	1.799***	4.471***	6.631***	0.433**	−0.173
	（0.279）	（0.640）	（2.001）	（0.213）	（0.112）
SPR	7.302***	8.833***	27.102***	3.326***	−0.503*
	（0.732）	（0.914）	（5.967）	（0.636）	（0.282）
N	111,087	111,087	111,087	111,087	111,087
${\bar{R}}^2$	0.681	0.509	0.363	0.247	0.036

（注）第1行は被説明変数を表す。ω_rとω_fはそれぞれリターンとOFIの撹乱項の標準偏差、${\tau }_r^2$と${\tau }_f^2$はそれぞれリターン・ショックとフロー・ショックによる条件付き分散、$FDR={\tau }_f^2/({\tau }_r^2+{\tau }_f^2)$である。第1列は説明変数を表し、単位はデプスの逆数D⁻¹が1,000、イベント数NEが100万、イベントの平均サイズASEが1,000、平均スプレッドSPRが1である。定数項と5分区間のダミー変数および年のダミー変数は簡潔さのため割愛した。Nは推定に用いたサンプルサイズ、${\bar{R}}^2$は自由度修正済み決定係数を表す。括弧内の数値はロバスト標準誤差であり、*、**、***は、係数がそれぞれ10％、5％、1％の有意水準で有意であることを示す。

（出所）筆者作成。

一方、FDRについての回帰結果は特徴的であった。D⁻¹とSPRの係数は有意に負であり、市場の流動性が低く取引コストが高いときにFDRが減少することが示された。決定係数は他の変数に比べて著しく低く、図6で示されたように、FDRが他の変数とは大きく異なる変動をすることと整合的である。

6.  おわりに

本研究では、S&P 500 E-mini先物のBBOファイルから計算したリターンとOFIとの間の相互作用を、日内変動と内生性を考慮したSVARモデルを用いて分析した。具体的には、各日の15分区間ごとにSVARモデルを適用することで日内変動を考慮し、内生性はITHを利用して構造パラメータを推定することで処理した。

実証分析の結果、本稿で用いた手法は、リターンとOFIの系列相関および相互相関を捉えるのに有効であることが示され、先行研究で提示されたいくつかの知見が確認された。特に、本研究では、1秒区間で有意なプライス・インパクトとフロー・インパクトが示された。この結果は、Deuskar and Johnson（2011）の結果と整合的であり、内生性とOLS推定値の上方バイアスが確認された。また、内生性を考慮したITHによって推定したプライス・インパクトは、Cont et al.（2014）の単純化LOBモデルで示唆されたものと整合的であった。加えて、インパルス応答から、リターン・ショックとフロー・ショックの影響はどちらも1秒以内にほとんど消滅し、瞬時インパクトとロングラン・インパクトの日内変動がほぼ同じことが示された。さらに、推定されたパラメータと関連する変量は有意な日内変動を示し、市場の状態を反映するデプス、イベントの数、平均スプレッドなどの変数の変動と関連していることが示された。

今後の研究として、本稿で用いた手法を多変量に拡張することが考えられる。多変量SVARモデルでは、Eisler et al.（2012）やHautsch and Huang（2012）で行われているように、異なるオーダー・ブック・イベントをそれぞれ別々に扱うことができる。また、多変量モデルを用いることで、複数の市場における価格変化と注文の相互作用を分析することができる。Budish et al.（2015）は、S&P E-mini 500先物取引とS&P 500の上場投資信託（exchange traded fund）が、1日を通じてほぼ完全に相関していることを指摘している。複数の金融商品の価格変化と注文の関係を定式化することは、それらの市場における価格発見過程を考察するのに有効であると考えられるので、今後の研究課題として取り組みたい。

謝辞

本研究は、法政大学イノベーション・マネジメント研究センター、一橋大学経済研究所 共同利用・共同研究センター、JSPS 科研費 JP15K17037、16H036050、19H00588の助成を受けている。

1  ニューヨーク証券取引所や東京証券取引所などの主要取引所を含むほとんどの金融市場では、電子LOBシステムが採用されている。

2  Bagehot（1971）は、異質な情報を持つトレーダーを考慮したいわゆる非対称情報モデルの最初の研究であり、このアプローチはその後、Copeland and Galai（1983）、Kyle（1985）、Glosten and Milgrom（1985）、Easley and O’Hara（1987）、Admati and Pfleiderer（1988）、Foster and Viswanathan（1990）などの研究によって分析され、発展してきた。こうした研究のレビューについては、例えば、O’Hara（1995）やHasbrouck（2007）などを参照。

3  近年、ニューヨーク-シカゴ間の往復通信時間は8.1ミリ秒に短縮された。その詳細や高頻度取引の競争が引き起こす問題点については、Budish et al.（2015）を参照。

4  多くの先行研究で、市場の活発さを表す変数は取引時間帯にU字型のパターンを示すことが観察されている。そのような変数は、寄り付き後に比較的高く、徐々に減少し、日の中頃に最低になり、その後、大引けまで増加する。また、寄り付き直後の値が大引け直前の値よりも低い、もしくは高いという非対称な形状になることもある。このような非対称なパターンは、J字型や逆J字型と呼ばれることもある。例えば、Wood et al.（1985）は、ニューヨーク証券取引所に上場している株式を分析し、分単位の平均リターンではU字型、リターンの変動では逆J字型のパターンを報告している。また、McInish and Wood（1992）は、分単位のビッド・アスク・スプレッドについてJ字型に近いパターンを報告し、Lee et al.（1993）は、30分ごとの出来高とビッド・アスク・スプレッドについてU字型のパターンを報告している。さらに、Andersen and Bollerslev（1997）は、S&P 500株価指数先物の5分間のリターンの絶対値について、大引け前に急激な低下や上昇があるものの、概ねU字型のパターンを報告している。

5  LOB市場における最適な取引戦略については、例えば、Obizhaeva（2008）やObizhaeva and Wang（2013）を参照。

6  ITHは、VAR分析におけるショックの識別によく用いられる。例えば、Rigobon and Sack（2003, 2004）やLanne and Lütkepohl（2008）では、金融政策のショックを特定するために残差分散の外生的変化を利用している。さまざまな分散不均一性の構造を利用したモデルについては、Lütkepohl and Netšunajev（2017）を参照。

7  S&P 500 E-mini先物は流動性の高い資産であり、S&P 500の価格発見のほとんどはE-mini市場で行われる（例えば、Hasbrouck（2003）を参照）。最小取引単位は先物価格の50倍、最小ティックサイズは0.25指数ポイントで、12.5ドル（=50×0.25）に相当する。月曜から金曜まで、ほぼ24時間取引されている。通常の取引は、シカゴ時間（夏時間）の8:30に始まり、15:15に終わる。15分間の休憩後、15:30から8:30まで電子取引が可能だが、16:30～17:00はメンテナンスで取引できない。限月は3月、6月、9月、12月で、最新の5限月が取引可能で、限月の第3金曜日の8:30まで取引できる。

8  観測データが不十分な日（主に休日の前後、祝日の前後、年末近くなど）は、標本から除外した。

9  典型的には、最も活発な限月は、直近の限月の最終取引日の約1週間前に直近の限月から次の限月に切り替わる。

10  注文の種類が利用可能な場合、つまり、注文がビッドまたはアスクの成行注文、指値注文、キャンセルに分類されている場合、ftを次のように計算することができる。

  

$$f_t=L_t^b-C_t^b-M_t^b-L_t^a+C_t^a+M_t^a$$

ここで、$M_t^b$, $M_t^a$, $L_t^b$, $L_t^a$, $C_t^b$, $C_t^a$は、ベスト・ビッドとベスト・アスクの価格での成行注文、指値注文、キャンセルを、それぞれt番目の1秒区間で足し合わせたものである。

11  Deuskar and Johnson（2011）は、内生性の原因を、Obizhaeva（2008）やObizhaeva and Wang（2013）で議論されているような、未処理のまま放置された指値注文や価格連動型の取引戦略の存在に求めている。

12  より一般的な設定での推定手順と識別条件については、Rigobon（2003）を参照。

13  Deuskar and Johnson（2011）は、推定されたプライス・インパクトを無条件のプライス・インパクトと呼んでいる。時変的な条件付きプライス・インパクトを調べるために、彼らは、いくつかのレベル（BBOよりも深いレベル）のデプスを通る直線の傾きとして計算されるILOBS（inverse slope of the limit order book）と呼ばれる指標を提案した。ILOBSは、取引に伴う価格変化を捉えるように設計されているため、潜在的な取引のプライス・インパクトの尺度となる。彼らは、ILOBSを用いて、時変的なプライス・インパクトをb_r,t=b₀+b₁ILOBS_tとして計算した。

14  Deuskar and Johnson（2011）は、条件付プライス・インパクトをb₀+b₁ILOBSと推定している。ここで、ILOBSは1分区間で計算された非流動性指標である。彼らの表2と表4によると、2008年2月から2009年1月までのILOBSの平均値は0.52、b₀=0.11、b₁=0.70である。したがって、条件付きプライス・インパクトの平均値は、0.11+0.70×0.52=0.474と近似的に計算される。

15  脚注14で条件付きプライス・インパクトを計算した期間に相当する2008年2月から2009年1月にかけて、ITHによるb_rの推定値はより高くより大きな変動を示し、平均値は0.834から1.769に、標準偏差は0.999から1.669に増加した。したがって、サンプル期間の違いは、プライス・インパクトの差の主な原因ではない。

参考文献

•  Admati,  A. R., &  Pfleiderer,  P. (1988). A theory of intraday patterns: Volume and price variability. Review of Financial Studies, 1(1): 3–40.
•  Andersen,  T. G., &  Bollerslev,  T. (1997). Intraday periodicity and volatility persistence in financial markets. Journal of Empirical Finance, 4(2–3): 115–158.
•  Andersen,  T. G., &  Bollerslev,  T. (1998). Deutsche mark-dollar volatility: Intraday activity patterns, macroeconomic announcements, and longer run dependencies. Journal of Finance, 53(1): 219–265.
•  Bagehot,  W. (1971). The only game in town. Financial Analysts Journal, 27(2): 12–14.
•  Boehmer,  E.,  Saar,  G., &  Yu,  L. (2005). Lifting the Veil: An Analysis of Pre-trade Transparency at the NYSE. Journal of Finance, 60(2): 783–815.
• Bouchaud, J.-P., Farmer, J. D., & Lillo, F. (2009). How markets slowly digest changes in supply and demand. In Hens, T. and Schenk-Hopp´e, K. R., editors, Handbook of Financial Markets: Dynamics and Evolution, chapter 2, pages 57–160. Elsevier, 1st edition.
•  Bouchaud,  J.-P.,  Gefen,  Y.,  Potters,  M., &  Wyart,  M. (2004). Fluctuations and response in financial markets: the suble nature of ‘random’ price changes. Quantitative Finance, 4(2): 176–190.
•  Bouchaud,  J.-P.,  Kockelkoren,  J., &  Potters,  M. (2006). Random walks, liquidity molasses and critical response in financial markets. Quantitative Finance, 6(2): 115– 123.
•  Bouchaud,  J.-P.,  Mézard,  M., &  Potters,  M. (2002). Statistical properties of stock order books: empirical results and models. Quantitative Finance, 2(4): 251–256.
•  Budish,  E.,  Cramton,  P., &  Shim,  J. (2015). The high-frequency trading arms race: Frequent batch auctions as a market design response. Quarterly Journal of Economics, 130(4): 1547–1621.
•  Chung,  K. H.,  Li,  M., &  McInish,  T. H. (2005). Information-based trading, price impact of trades, and trade autocorrelation. Journal of Banking & Finance, 29(7): 1645–1669.
•  Cont,  R.,  Kukanov,  A., &  Stoikov,  S. (2014). The price impact of order book events. Journal of Financial Econometrics, 12(1): 47–88.
•  Copeland,  T. E., &  Galai,  D. (1983). Information effects on the bid-ask spread. Journal of Finance, 38(5): 1457–1469.
•  Deuskar,  P., &  Johnson,  T. C. (2011). Market Liquidity and Flow-driven Risk. Review of Financial Studies, 24(3): 721–753.
•  Dufour,  A., &  Engle,  R. F. (2000). Time and the price impact of a trade. Journal of Finance, 55(6): 2467–2498.
•  Easley,  D.,  Kiefer,  N. M., &  O’Hara,  M. (1997a). The informaiton content of the trading process. Journal of Empirical Finance, 4(2–3): 159–186.
•  Easley,  D.,  Kiefer,  N. M., &  O’Hara,  M. (1997b). One day in the life of a very common stock. Review of Financial Studies, 10: 805–835.
•  Easley,  D., &  O’Hara,  M. (1987). Price, trade size, and information in securities markets. Journal of Financial Economics, 19(1): 69–90.
•  Easley,  D., &  O’Hara,  M. (1992). Time and the Process of Security Price Adjustment. Journal of Finance, 47(2): 577–605.
•  Eisler,  Z.,  Bouchaud,  J.-P., &  Kockelkoren,  J. (2012). The price impact of order book events: Market orders, limit orders and cancellations. Quantitative Finance, 12(9): 1395–1419.
•  Foster,  F. D., &  Viswanathan,  S. (1990). A theory of the interday variations in volume, variance, and trading costs in securities markets. Review of Financial Studies, 3(4): 593–624.
•  Glosten,  L. R., &  Milgrom,  P. R. (1985). Bid, ask and transaction prices in a special- ist market with heterogeneously informed traders. Journal of Financial Economics, 14(1): 71–100.
•  Hansen,  L. P. (1982). Large sample properties of generalized method of mements estimators. Econometrica, 50(4): 1029–1054.
•  Hasbrouck,  J. (1991). Measuring the Information Content of Stock Trades. Journal of Finance, 46(1): 179–207.
•  Hasbrouck,  J. (2003). Intraday price formation in u.s. equity index markets. Journal of Finance, 58(6): 2375–2399.
• Hasbrouck, J. (2007). Empirical Market Microstructure: The Institutions, Economics and Econometrics of Securities Trading. Oxford University Press, New York.
•  Hautsch,  N.,  Hess,  D., &  Veredas,  D. (2011). The impact of macroeconomic news on quote adjustments, noise, and informational volatility. Journal of Banking & Finance, 35(10): 2733–2746.
•  Hautsch,  N., &  Huang,  R. (2012). The market impact of a limit order. Journal of Economic Dynamics and Control, 36(4): 501–522.
•  Jones,  C. M.,  Kaul,  G., &  Lipson,  M. L. (1994a). Information, trading, and volatil- ity. Journal of Financial Economics, 36(1): 127–154.
•  Jones,  C. M.,  Kaul,  G., &  Lipson,  M. L. (1994b). Transactions, volume, and volatility. Review of Financial Studies, 7(4): 631–651.
•  Kyle,  A. S. (1985). Continuous Auctions and Insider Trading. Econometrica, 53(6): 1315–1335.
•  Lanne,  M., &  Lütkepohl,  H. (2008). Indentifying monetary policy shocks via changes in volatility. Journal of Money, Credit and Banking, 40(6): 1131–1149.
•  Lee,  C. M. C.,  Mucklow,  B., &  Ready,  M. J. (1993). Spreads, depths, and the impact of earnings information: An intraday analysis. Review of Financial Studies, 6(2): 345–374.
•  Lütkepohl,  H., &  Netšunajev,  A. (2017). Structural vector autoregressions with het- eroskedasticity: A review of different volatility models. Econometrics and Statistics, 1: 2–18.
•  McInish,  T. H., &  Wood,  R. A. (1992). An Analysis of Intraday Patterns in Bid/Ask Spreads for NYSE Stocks. The Journal of Finance, 47(2): 753.
• Obizhaeva, A. (2008). Price Impact and Spread: Application of Bias-Free Estimation Methodology to Portfolio Transitions. Working Paper.
•  Obizhaeva,  A. A., &  Wang,  J. (2013). Optimal trading strategy and supply/demand dynamics. Journal of Financial Markets, 16(1): 1–32.
• O’Hara, M. (1995). Market Microstructure Theory. Blackwell, Oxford.
•  Rigobon,  R. (2003). Identification through heteroskedasticity. Review of Economics and Statistics, 85(4): 777–792.
•  Rigobon,  R., &  Sack,  B. (2003). Measuring the reaction of monetary policy to the stock market. The Quarterly Journal of Economics, 118: 639–669.
•  Rigobon,  R., &  Sack,  B. (2004). The impact of monetary policy on asset prices. Journal of Monetary Economics, 51: 1553–1575.
•  Sentana,  E., &  Fiorentini,  G. (2001). Identification, estimation and testing of conditionally heteroskedastic factor models. Journal of Econometrics, 102(2): 143–164.
•  Wood,  R. A.,  McInish,  T. H., &  Ord,  J. K. (1985). An Investigation of Transactions Data for NYSE Stocks. The Journal of Finance, 40(3): 723–739.