Predicting Method for the Human Plasma Concentration–Time Profile of a Monoclonal Antibody from the Half-life of Non-human Primates

Abstract

Efficiency (speed and cost) and animal welfare are important factors in the development of new drugs. A novel method (the half-life method) was developed to predict the human plasma concentration–time profile of a monoclonal antibody (mAb) after intravenous (i.v.) administration using less data compared to the conventional approach; moreover, predicted results were comparable to conventional method. This new method use human geometric means of pharmacokinetics (PK) parameters and the non-human primates (NHP) half-life of each mAb. PK data on mAbs in humans and NHPs were collected from literature focusing on linear elimination, and the two-compartment model was used for analysis. The following features were revealed in humans: 1) the coefficient of variation in the distribution volume of the central compartment and at steady state of mAbs was small (22.6 and 23.8%, respectively) and 2) half-life at the elimination phase (t1/2_β) was the main contributor to plasma clearance. Moreover, distribution volume showed no significant correlation between humans and NHPs, and human t1/2_β showed a good correlation with allometrically scaled t1/2_β of NHP. Based on the features revealed in this study, we propose a new method for predicting the human plasma concentration–time profile of mAbs after i.v. dosing. When tested, this half-life method showed reasonable human prediction compared with a conventional empirical approach. The half-life method only requires t1/2_β to predict human PK, and is therefore able to improve animal welfare and potentially accelerate the drug development process.

INTRODUCTION

Non-clinical pharmacokinetic studies are conducted to predict human pharmacokinetics (PK) for drug development.¹⁾ In addition to efficiency, such as speed and cost, animal welfare is another important aspect in recent circumstances.²⁾ Unfortunately, blood must be drawn and sampled more than 10 times in non-human primates (NHP) studies for PK analysis.^3,4) A method of predicting human PK that requires less data would be preferable, both in terms of efficiency and animal welfare.⁵⁾

Progress in technology related to recombinant DNA and hybridomas for monoclonal antibodies (mAbs) has increased the use of active peptides, proteins, and mAbs for therapeutic purposes.^6,7) A significant feature of these biologics is that their interactions with a specific receptor or antigen mediate their distribution and elimination.⁸⁾ Active peptides, such as erythropoietin (EPO) and granulocyte-colony stimulating factor (G-CSF), are cleared from circulating blood not only by receptor-mediated (non-linear) elimination but also by linear elimination, for which the linear clearance (CL) can be predicted by allometric scaling.^9,10) In recent years, numerous therapeutic mAbs have come on the market, and new candidates are continuously being developed for cancer, autoimmune disorders, and other diseases.^11,12) As well as binding to other biologics, mAbs can also bind to membrane antigen, in which case their elimination processes are both non-linear and linear.¹³⁾ Antibodies can avoid cellular degradation by recycling the mechanisms of human neonatal Fc receptor (FcRn) and, therefore, have a long circulating half-life in healthy humans (7–21 d).¹⁴⁾ The prediction of a human plasma concentration–time profile with non-linear elimination is difficult and complex, requiring the inclusion of numerous factors, e.g., the target antigen and mAb-target complex turn-over rate, the antigen synthesis rate, and mAb affinity to the target antigen.¹⁵⁾ For these reasons, we focused on predicting linear elimination in this report.

In a report by Dirks and Meibohm that reviewed the human population PK parameters of therapeutic mAbs, the PK data exhibited a bi-exponential decay pattern of linear elimination after intravenous (i.v.) administration, and a number of mAbs were analyzed by the two-compartment model.¹⁶⁾ Their report indicated that, because the distribution of mAbs is restricted by their large molecular weight and high hydrophilicity, the distribution volume at central (V1) and at peripheral (V2) were typically small in humans.

This similarity in the PK features suggests that some values for PK parameters of mAbs may be common in humans. If so, these parameters would not need to be extrapolated from NHP values. Therefore, in this study, the human PK parameters of mAbs in published data were collected and analyzed to determine whether parameters extrapolated from NHPs are needed to predict the human plasma concentration–time profile after i.v. dosing.

Predictions about human CL and plasma concentration–time profile are an important part of drug development, especially prior to first-in-human clinical studies.¹⁷⁾ Predicting human CL by allometry has been reported using multiple species,^18,19) including cynomolgus monkeys,^20–23) transgenic mice expressing human FcRn,^24,25) and minipigs.²⁶⁾ Of these species, the cynomolgus monkey is the most frequently selected for preclinical studies to predict human CL. In addition to human CL, human plasma concentration–time profiles have also been predicted, both empirically and mechanistically. As shown in Fig. 1, examples of empirical approaches are allometric scaling of two-compartment model parameters,^13,27) and Dedrick plot^28,29) while an example of the mechanistic approach is the physiologically based pharmacokinetics model (PBPK).^30–32) However, an empirical approach based on human PK for predicting human plasma concentration–time profile of mAbs after i.v. dosing has not been reported. This report proposes the half-life method of prediction in humans, using human geometric means and the allometric scaled t1/2_β of NHP.

Fig. 1. Current Schematic for Predicting Human PK Parameters and Profiles That Exhibit Linear PK

MATERIALS AND METHODS

Data Collection

The main search objectives were therapeutic mAbs approved by the FDA (Food and Drug Administration, U.S.A.) or PMDA (Pharmaceutical and Medical Devices Agency, Japan) before the end of 2015. Moreover, some agents under clinical development were also added to the dataset, which consisted of data on human PK after i.v. administration (24 mAbs),^33–55) cynomolgus monkey PK after i.v. administration (15 mAbs),^{4,33,39,42,44,49,51,55–61)} and rhesus monkey PK after i.v. administration (4 mAbs).^3,52,62,63) The PK of mAbs with linear PK in both humans and NHPs were analyzed and the parameter values of the selected mAbs are listed in the table in Supplementary 1. When two-compartment model parameters could not be obtained from literature, two-compartment model analysis was conducted on the data captured for serum/plasma mean concentration versus time using digitizer software UnGraph Version 5.0 (HULINKS, Tokyo, Japan).

Pharmacokinetic Data Analysis

The serum/plasma mean concentration–time profiles after i.v. administration were analyzed by the two-compartment open model using Phoenix WinNonlin version 6.0 (Certara Inc., Princeton NJ, U.S.A.). The serum/plasma concentration (C) declined in a bi-exponential fashion using first macro-constant (A), second macro-constant (B), first rate constant (α), and second rate constant (β).

  

(1)

Central elimination rate (K10), central to peripheral distribution rate (K12), and peripheral to central distribution rate (K21) were obtained according to the following equations:

  

(2)

  

(3)

  

(4)

  

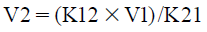(5)

The distribution volume in central compartment (V1) was calculated as Dose/(A + B); the distribution volume at steady state (V_dss) was calculated as V1 + V2; t1/2_β was calculated as Ln (2)/β.

The AUC was calculated by the following equations:

  

(6)

  

(7)

  

(8)

The total body CL was estimated as Dose/AUC_inf, and the distribution volume at the elimination phase (V_dβ) was calculated as CL/β.

Prediction of Human Elimination Rate Constants in the Elimination Phase Using Allometric Scaling

The human β of mAbs was predicted based on NHP data using the simple allometric equation:

  

(9)

β_human and β_NHP are elimination rates at the distribution phase in humans and NHPs, respectively. BW_human is the human body weight and BW_NHP is the cynomolgus monkey or rhesus monkey body weight. If no specific body weight information was found in literature, a weight of 70 kg for humans, 3.75 kg for cynomolgus monkeys, or 6.0 kg for rhesus monkeys was used.²⁰⁾ X is the scaling exponent for rate constant (−0.15).²¹⁾

Predicting Human Plasma Concentration–Time Profiles by the Half-life Method

The human plasma concentration–time profiles after i.v. dosing were predicted from NHP t1/2_β. For the half-life method, the human geometric mean values for V1_human, V_dsshuman, K12_human, K21_human were set as 45.1, 81.0 mL/kg, 0.275, 0.355 d⁻¹, respectively (Table 1). K10_human was approximated by the following equation:

  

(10)

Table 1. Geometric Mean and CV of Two-Compartment Model Parameters and Distribution Volume at Steady State in Humans (24 mAb)

Parameters	K10 d−1	K12 d−1	K21 d−1	V1 mL/kg	Vdss mL/kg
Geometric mean	0.0832	0.275	0.355	45.1	81.0
Geometric CV (%)	57.8	92.9	96.1	22.6	23.8

β_human was calculated by Eq. 9 and V_dsshuman was taken to be 81.0 mL/kg, as above.

To simulate the human plasma concentration–time profile after i.v., the two-compartment model described in Eq. 1 was used.

  

(11)

  

(12)

  

(13)

  

(14)

Prediction of Human Plasma Concentration–Time Profiles by Allometric Scaling

The human plasma concentration–time profiles after i.v. dosing were predicted using allometrically scaled NHP parameters in the two-compartment model.^13,27) Scaling was conducted following Eq. 9, and scaling exponents were 1.0 and −0.15 for V1 and rate constants (K10, K12, and K21), respectively. To simulate the human plasma concentration–time profile after i.v. dosing, the two-compartment model described in Eqs. 1 and 11–14 was adopted.

RESULTS

Human Two-Compartment Model Parameters after i.v. Administration

Table 1 lists the human geometric mean values from 24 mAbs for two-compartment model parameters. Although, K12 and K21 had large coefficients of variation (CV) with 92.9 and 96.1%, the CV of V1 and V_dss were small at 22.6 and 23.8%, respectively. Therefore, the ratio between K12 and K21 would be constant.

Two-Compartment Model Analysis of Human mAb PK after i.v. Administration

Using the two-compartment model parameters for the collected human PK data of 24 mAbs, the PK features in humans were analyzed. The human serum/plasma concentration–time profile consisted of the distribution phase with a short half-life and the elimination phase with a long half-life. In the simulated human PK profile using human geometric means for the two-compartment model parameters, the distribution phase ceased to contribute from 2.24 d after i.v. dosing because the elimination phase accounted for over 80% of serum/plasma concentration from that time. In the dose-normalized PK profile, the differences in serum/plasma concentration within the distribution phase were small, and the difference in PK between mAbs emerged in the elimination phase (Fig. 2A). Raxibacumab shows a human PK profile that is typical of two-compartment model analysis after i.v. (Fig. 2B). AUC_inf was mainly covered by AUC_β in human after i.v. dosing, and the contribution percentage to AUC_inf exceeded 90% (Fig. 2C). Therefore, CL could be evaluated by AUC_β. Additionally, V_dss showed approximately comparable values with V_dβ, and t1/2_β showed an inverse correlation with CL (R² = 0.824) (Figs. 2D, 2E). These features indicate that prediction of human t1/2_β is needed for predicting the human plasma concentration–time profile.

Fig. 2. Two-Compartment Model Analysis of Monoclonal Antibodies after Intravenous (i.v.) Administration in Human

(A) Dose-normalized human PK profile for 24 mAbs analyzed by the two-compartment model (dotted lines) and simulated human PK profile using human geometric mean values (solid line). (B) A typical concentration–time profile found by the two-compartment model (raxibacumab). (C) Fraction percentages of exposure in human for the distribution phase (AUC_α) and elimination phase (AUC_β), respectively. (D) Relationship between distribution volume at steady state (V_dss) and distribution volume at elimination phase (V_dβ) in human. Solid diagonal line represents line of unity. The dotted lines represent two-fold range above and below the line of unity. (E) Relationship between human clearance (CL) and half-life at elimination phase (t1/2_β) in human. The dotted line is the regression (exponential regression) line.

Distribution-Related PK Parameters

Distribution volume was analyzed using data from 24 mAbs for humans and 19 mAbs for NHPs. There was no correlation in V1 and V_dss between humans and NHPs (Figs. 3A, 3B) and furthermore, the scatter plots of V1 and V_dss in both species showed the values centralized to a geometric mean; therefore, each species had specific values for the distribution parameters of mAbs, and the geometric mean values (CV%) of V_dss in humans and NHPs were 81.0 mL/kg (23.8) and 71.1 mL/kg (35.3), respectively. The relationship between human K12 and K21 was represented by the equation K21 = 1.32 × K12 (R² = 0.665) (Fig. 3C), and this correlation indicated that the ratio was constant between V1 and V2. Moreover, these results corresponded to the small CV of V_dss among mAbs.

Fig. 3. Distribution Related PK Parameters after i.v. Administration

(A) Human distribution volume of central compartment (V1) is plotted against NHP V1. (B) Human distribution volume at steady state (V_dss) is plotted against NHP V_dss. (C) Relationship between human central to peripheral distribution rate (K12) and human peripheral to central distribution rate (K21). The dotted line is the regression (linear regression) line.

Prediction of Human t1/2_β from t1/2_β of NHP by Allometric Scaling

As explained earlier, predicting the human t1/2_β was important for predicting the human plasma concentration–time profile, so allometric scaling for predicting human t1/2_β from the NHP t1/2_β was calculated. Allometric scaling was conducted for NHP data on 19 mAbs, and the scaled values were plotted against human values (Fig. 4). Allometric scaling by 78.9 and 89.5% of the NHP t1/2_β gave predictions that were within 2- and 3-fold of actual human t1/2_β, respectively. Therefore, human t1/2_β could be predicted from NHP t1/2_β with allometric scaling.

Fig. 4. Correlation between Reported Human t1/2_β and Predicted Human t1/2_β

Predicted values for human t1/2_β were plotted against observed values for human t1/2_β. Human t1/2_β was predicted from NHP data using simple allometry with the exponent of −0.15. When body weight was not reported, it was calculated using 70 kg in human, 6 kg in rhesus monkey, and 3.75 kg in cynomolgus monkey . Solid, dotted, and dashed gray lines indicate 100%, 50–200%, and 33–300% prediction, respectively. Solid diagonal line represents line of unity. The dotted lines represent two-fold range above and below the line of unity. The dashed lines represent three-fold range above and below the line of unity.

The Half-life Method for Predicting Human Plasma Concentration–Time Profile after i.v. Administration

To predict the human plasma concentration–time profile after i.v. dosing, we propose the half-life method, which only requires data on t1/2_β from NHP (Fig. 5). Based on the above findings on human PK, it was not necessary to extrapolate values from non-clinical data to predict human V1, K12, K21, which mainly contribute to the distribution phase for the human plasma concentration–time profile of mAbs. In the half-life method, human geometric mean values were applied to V1, K12, and K21. Finally, K10 was estimated using allometrically scaled β of NHP and the human geometric means of V1 and V_dss.

Fig. 5. Proposed Half-life Method Using Only Data on t1/2_β from NHP to Predict mAb Human PK

NHP, non-human primate; PK, pharmacokinetics; V1, distribution volume of central compartment; K12, central to peripheral distribution rate; K21, peripheral to central distribution rate; β, elimination rate constant at elimination phase; BW, body weight; K10, central elimination rate; V_dss, distribution volume at steady state.

Human t1/2_β Predicted by the Half-life Method Using Only NHP t1/2_β

The half-life method was verified for 19 mAbs for which PK data after i.v. dosing both in humans and NHPs were available. With the proposed method, all of the values predicted for human K10 of mAbs were within 2-fold of the predicted value using allometric scaling (Fig. 6). The difference in the parameter values predicted with allometric scaling exceeds 2-fold in about 20% of mAbs (Fig. 4). Therefore, when predicting the human plasma concentration–time profile, the half-life method using only NHP t1/2_β successfully obtained estimations comparable to those from a two-compartment model analysis with allometric scaling.

Fig. 6. Comparison of Predicted Human K10 Using Half-life Method and Allometric Scaling Method

Predicted human K10 by half-life method were plotted against predicted values using allometric scaling method. Solid diagonal line represents line of unity. The dotted lines represent two-fold range above and below the line of unity.

DISCUSSION

In this study, a novel prediction method (the half-life method), which uses only t1/2_β from NHP data, was developed to predict the human plasma concentration–time profile of mAbs after i.v. administration (Fig. 5). The half-life method is based on features of human and NHP PK revealed in this report. Moreover, the results from this new approach were comparable with those from conventional approaches, such as the allometric scaling and Dedrick methods.

According to the data we collected, mAbs exhibit bi-phased elimination decay after i.v. dosing in humans (Fig. 2A), so a two-compartment model analysis was also conducted, giving CV values for human V1 and V_dss of about 20% (Table 1). The margin of error for these CV values is comparable with quantification methods; for example, in guidelines for a ligand-binding assay generally used to quantify mAbs, precision and accuracy are defined as within 20%.⁶⁴⁾ Additionally, the geometric mean of V1 was comparable to the plasma volume in humans and NHPs.⁶⁵⁾ These small differences in CV supported the idea that distribution of mAbs would be strictly limited by their large molecular weight and high hydrophilicity. Almost all AUC_inf consisted of AUC_β in human, and CL could be evaluated by plasma concentration at the elimination phase (Fig. 2C). The values of V_dβ were similar among mAbs, and t1/2_β had inverse correlation to CL (Fig. 2E). Moreover, these PK features were common in humans and NHPs, so CL also showed an inverse correlation to t1/2_β in NHPs (data not shown). Generally, human CL is predicted from the CL of NHP by allometric scaling using 0.85 as the scaling exponent; therefore, human t1/2_β could be predicted from t1/2_β of NHP using the same scaling exponent²¹⁾ (−0.15 as rate)²¹⁾ (Fig. 4). These results indicated that to predict the human plasma concentration–time profile, V1, V_dss parameters did not need to be extrapolated from NHP values.

We proposed the half-life method for predicting the human plasma concentration–time profile of mAbs after i.v. dosing based on features revealed in the data collected from literature. A human geometric mean value was applied to predict V1 because the CV value among mAbs was small. Although human K12 and K21 showed large differences between the 24 mAbs, the ratios between K12 and K21 were similar (Fig. 3C). Moreover, the contribution of the distribution phase to AUC_inf in humans was small. Therefore, the human geometric means were adopted for K12 and K21. In human PK of mAbs, AUC_β was a main contributor to exposure, and V_dss was approximated as V_dβ (Figs. 2C, 2D), which led to the following approximations: CL = K10 × V1 = β × V_dβ ≈ β × V_dss, and K10 were calculated following Eq. 9. The same relationship was confirmed in NHP, and human β (β = Ln(2)/t1/2_β) could be predicted from the t1/2_β of NHP. Therefore, human β was predicted by extrapolating from NHP data, using a scaling exponent of −0.15. A human geometric mean value was applied to calculate V_dss because of the small variation among mAbs. Accordingly, human K10 could be predicted from the t1/2_β of NHP. The values for predicted human t1/2_β were comparable between the half-life method and a conventional method (Fig. 6, Supplementary 2).

The half-life method predicted similar values for human t1/2_β compared with two empirical methods commonly used to predict the human plasma concentration–time profile of mAbs: the two-compartment model with allometric scaling and the Dedrick plot.^13,27–29) The values for human t1/2_β predicted by the half-life method and this two-compartment model are comparable because: 1) distribution parameters showed little variation both in humans and NHPs; 2) AUC_β was the main contributor to AUC_inf in both species; and 3) human CL could be predicted from NHP CL. Although there was a less than 2-fold difference in the predicted human K10 for all mAbs, cetuximab, nivolumab, and humicade showed a different PK profile (Supplementary 2). A mAb with a distribution phase of less than a day and another with a phase lasting close to one week could show two different predicted PK profiles, depending on whether the half-life or allometric method was used; this is because the half-life method only considers the elimination phase. Therefore, in vitro tools for evaluating the distribution phase are needed to improve efficiency in the prediction of human plasma concentration–time profiles. A Dedrick plot would predict similar results in humans as the half-life method, but the Dedrick plot is not model-based and could not be expanded to predict mAbs with non-linear elimination. For these reasons, the half-life method is simpler and more useful than conventional approaches. We found that, in the half-life method, a scaling exponent of −0.15 for t1/2_β was more accurate than a scaling exponent of −0.25; that is, 84.2 and 73.7% of estimates were within 2-fold of the actual values, respectively (data not shown). Therefore, the scaling exponent for the half-life method was determined as −0.15. Although only one example was tested, a satisfactory result was observed for motavizumab-YTE, a mAb mutated to have longer half-life in plasma, which suggests that the half-life method would be useful for predicting the PK of mutated mAbs.

A feature of EPO and G-CSF is their specific binding to a receptor, which means that receptor-mediated endocytosis contributes to the non-linear CL of these peptides.^9,10) Several mAbs exhibited non-linear PK because of the binding to membrane antigen, which is a biological mechanism of action. Therefore, predicting the plasma concentration–time profile of mAbs that have non-linear PK is important not only for PK but also for pharmacology and toxicology. Although several studies have been conducted to predict the PK in humans for mAbs that showed non-linearity, many of the mechanisms of non-linear PK still need to be thoroughly understood.^15,22) The models needed to predict non-linear PK in humans consist of non-linear and linear elimination processes.^13,27,32) The half-life method can elucidate the human plasma concentration–time profile for linear elimination, which may then contribute to predicting the non-linear elimination of a mAb.

The half-life method can contribute to the principle of Refinement as part of the 3Rs (Refinement, Reduction and Replacement) initiative. Avoiding unnecessary injections and blood draws palliates the pain suffered by animals and is important to animal welfare.⁵⁾ Unfortunately, blood must be drawn more than 10 times for PK analysis in NHP studies; it is drawn frequently in a short span of days after i.v. administration to evaluate the distribution phase. The conventional prediction method requires evaluating every PK profile after i.v. administration, whereas the half-life method does not need the distribution phase for NHPs, but only the t1/2_β (Refinement), and this value can be derived from plasma concentration data with just three time points in the elimination phase. Conventional PK studies utilizing frequent blood draws could be classified as category C according the SCAW system, however a lesser frequency of only three blood draws once a week frequency falls into Category B according to some institutional animal care and use committees (IACUCs).⁶⁶⁾

Furthermore, to improve animal welfare, it is also important to reduce the total number of animals used in such experiments. While the half-life method on its own does not fulfill the 3R initiative’s Reduction principle, it only requires NHP t1/2_β to predict the human plasma concentration-time profile, and this could already be provided by a related pharmacology or toxicology study.^67–69) Therefore, by using the half-life method to avoid an NHP PK study, we may indirectly reduce the number of animals involved in overall mAb development. This study was able to elucidate the features of human PK, and the human profile could be predicted using just the t1/2_β obtained from NHP. The half-life method uses just one parameter obtained from NHPs to predict human t1/2_β. Therefore, an in vitro assay system which evaluates human t1/2_β could replace an NHP study intended for the human plasma concentration–time profile prediction. Single PK parameters such as t1/2 have been evaluated in vitro, but there are no reports of in vitro systems able to evaluate all four parameters in two-compartment model for human PK prediction.^70–72) The comparable value of t1/2 can be substituted for t1/2_β in cases of mAbs with linear elimination. The combination of the half-life method and the in vitro evaluation of human t1/2 could further improve both efficiency and animal welfare in mAb development. In particular, speed would improve, because the evaluation of in vivo PK takes a long time due to the slow elimination from circulation. Replacing an NHP study performed for human PK profile prediction with an in vitro assay system would also reduce the number of NHPs involved.

In conclusion, to increase the efficiency of mAb development and in consideration for animal welfare, we have developed a half-life method that uses only the t1/2_β of NHPs to predict the human plasma concentration-time profile of mAbs. Moreover, the accuracy of this half-life method is comparable to that of conventional methods.

Acknowledgment

The authors thank Sally Matsuura and Jacob Davis for an advice in the preparation and the language editing of this paper.

Conflict of Interest

The authors declare no conflict of interest.

Supplementary Materials

The online version of this article contains supplementary materials.

REFERENCES

• 1) Iwasaki K, Uno Y, Utoh M, Yamazaki H. Importance of cynomolgus monkeys in development of monoclonal antibody drugs. Drug Metab. Pharmacokinet., 34, 55–63 (2019).
• 2) Raje AA, Mahajan V, Pathade VV, Joshi K, Gavali A, Gaur A, Kandikere V. Capillary microsampling in mice: effective way to move from sparse sampling to serial sampling in pharmacokinetics profiling. Xenobiotica, 1, 1–7 (2019).
• 3) Che J, Wang H, Chen Z, Li X, Hou Y, Shan C, Cheng Y. A new approach for pharmacokinetics of single-dose cetuximab in rhesus monkeys by surface plasmon resonance biosensor. J. Pharm. Biomed. Anal., 50, 183–188 (2009).
• 4) Nnane IP, Xu Z, Zhou H, Davis HM. Non-clinical pharmacokinetics, prediction of human pharmacokinetics and first-in-human dose selection for CNTO 5825, an anti-interleukin-13 monoclonal antibody. Basic Clin. Pharmacol. Toxicol., 117, 219–225 (2015).
• 5) Diehl KH, Hull R, Morton D, Pfister R, Rabemampianina Y, Smith D, Vidal JM, van de Vorstenbosch C. A good practice guide to the administration of substances and removal of blood, including routes and volumes. J. Appl. Toxicol., 21, 15–23 (2001).
• 6) Köhler G, Milstein C. Continuous cultures of fused cells secreting antibody of predefined specificity. Nature, 256, 495–497 (1975).
• 7) Whitcomb DC, O’Dorisio TM, Cataland S, Shetzline MA, Nishikawara MT. Identification of tissue insulin receptors: use of a unique in vivo radioreceptor assay. Am. J. Physiol., 249, 561–567 (1985).
• 8) Sugiyama Y, Hanano M. Receptor-mediated transport of peptide hormones and its importance in the overall hormone disposition in the body. Pharm. Res., 6, 192–202 (1989).
• 9) Kuwabara T, Kato Y, Kobayashi S, Suzuki H, Sugiyama Y. Nonlinear pharmacokinetics of a recombinant human granulocyte colony-stimulating factor derivative (nartograstim): species differences among rats, monkeys and humans. J. Pharmacol. Exp. Ther., 271, 1535–1543 (1994).
• 10) Kato M, Kamiyama H, Okazaki A, Kumaki K, Kato Y, Sugiyama Y. Mechanism for the nonlinear pharmacokinetics of erythropoietin in rats. J. Pharmacol. Exp. Ther., 283, 520–527 (1997).
• 11) Kaplon H, Reichert JM. Antibodies to watch in 2019. MAbs, 11, 219–238 (2019).
• 12) Ecker DM, Jones SD, Levine HL. The therapeutic monoclonal antibody market. MAbs, 7, 9–14 (2015).
• 13) Vugmeyster Y, Rohde C, Perreault M, Gimeno RE, Singh P. Agonistic TAM-163 antibody targeting tyrosine kinase receptor-B: applying mechanistic modeling to enable preclinical to clinical translation and guide clinical trial design. MAbs, 5, 373–383 (2013).
• 14) Tabrizi MA, Tseng CM, Roskos LK. Elimination mechanisms of therapeutic monoclonal antibodies. Drug Discov. Today, 11, 81–88 (2006).
• 15) Singh AP, Krzyzanski W, Martin SW, Weber G, Betts A, Ahmad A, Abraham A, Zutshi A, Lin J, Singh P. Quantitative prediction of human pharmacokinetics for mAbs exhibiting target-mediated disposition. AAPS J., 17, 389–399 (2015).
• 16) Dirks NL, Meibohm B. Population pharmacokinetics of therapeutic monoclonal antibodies. Clin. Pharmacokinet., 49, 633–659 (2010).
• 17) Wang J, Iyer S, Fielder PJ, Davis JD, Deng R. Projecting human pharmacokinetics of monoclonal antibodies from nonclinical data: comparative evaluation of prediction approaches in early drug development. Biopharm. Drug Dispos., 37, 51–65 (2016).
• 18) Mahmood I. Interspecies scaling of protein drugs: prediction of clearance from animals to humans. J. Pharm. Sci., 93, 177–185 (2004).
• 19) Wang W, Prueksaritanont T. Prediction of human clearance of therapeutic proteins: simple allometric scaling method revisited. Biopharm. Drug Dispos., 31, 253–263 (2010).
• 20) Ling J, Zhou H, Jiao Q, Davis HM. Interspecies scaling of therapeutic monoclonal antibodies: initial look. J. Clin. Pharmacol., 49, 1382–1402 (2009).
• 21) Deng R, Iyer S, Theil FP, Mortensen DL, Fielder PJ, Prabhu S. Projecting human pharmacokinetics of therapeutic antibodies from nonclinical data: what have we learned? MAbs, 3, 61–66 (2011).
• 22) Dong JQ, Salinger DH, Endres CJ, Gibbs JP, Hsu CP, Stouch BJ, Hurh E, Gibbs MA. Quantitative prediction of human pharmacokinetics for monoclonal antibodies: retrospective analysis of monkey as a single species for first-in-human prediction. Clin. Pharmacokinet., 50, 131–142 (2011).
• 23) Oitate M, Masubuchi N, Ito T, Yabe Y, Karibe T, Aoki T, Murayama N, Kurihara A, Okudaira N, Izumi T. Prediction of human pharmacokinetics of therapeutic monoclonal antibodies from simple allometry of monkey data. Drug Metab. Pharmacokinet., 26, 423–430 (2011).
• 24) Tam SH, McCarthy SG, Brosnan K, Goldberg KM, Scallon BJ. Correlations between pharmacokinetics of IgG antibodies in primates vs. FcRn-transgenic mice reveal a rodent model with predictive capabilities. MAbs, 5, 397–405 (2013).
• 25) Avery LB, Wang M, Kavosi MS, Joyce A, Kurz JC, Fan YY, Dowty ME, Zhang M, Zhang Y, Cheng A, Hua F, Jones HM, Neubert H, Polzer RJ, O’Hara DM. Utility of a human FcRn transgenic mouse model in drug discovery for early assessment and prediction of human pharmacokinetics of monoclonal antibodies. MAbs, 8, 1064–1078 (2016).
• 26) Zheng Y, Tesar DB, Benincosa L, et al. Minipig as a potential translatable model for monoclonal antibody pharmacokinetics after intravenous and subcutaneous administration. MAbs, 4, 243–255 (2012).
• 27) Li H, Kock K, Wisler JA, Rees WA, Prince PJ, Reynhardt KO, Hsu H, Yu Z, Borie DC, Salinger DH, Pan WJ. Prediction of clinical pharmacokinetics of AMG 181, a human anti-α 4 β 7 monoclonal antibody for treating inflammatory bowel diseases. Pharmacol. Res. Perspect., 3, e00098 (2015).
• 28) Oitate M, Nakayama S, Ito T, Kurihara A, Okudaira N, Izumi T. Prediction of human plasma concentration–time profiles of monoclonal antibodies from monkey data by a species–invariant time method. Drug Metab. Pharmacokinet., 27, 354–359 (2012).
• 29) Xiang H, Bender BC, Reyes AE 2nd, Merchant M, Jumbe NL, Romero M, Davancaze T, Nijem I, Mai E, Young J, Peterson A, Damico-Beyer LA. Onartuzumab (MetMAb): using nonclinical pharmacokinetic and concentration–effect data to support clinical development. Clin. Cancer Res., 19, 5068–5078 (2013).
• 30) Baxter LT, Zhu H, Mackensen DG, Butler WF, Jain RK. Biodistribution of monoclonal antibodies: scale-up from mouse to human using a physiologically based pharmacokinetic model. Cancer Res., 55, 4611–4622 (1995).
• 31) Davda JP, Jain M, Batra SK, Gwilt PR, Robinson DH. A physiologically based pharmacokinetic (PBPK) model to characterize and predict the disposition of monoclonal antibody CC49 and its single chain Fv constructs. Int. Immunopharmacol., 8, 401–413 (2008).
• 32) Glassman PM, Balthasar JP. Physiologically-based pharmacokinetic modeling to predict the clinical pharmacokinetics of monoclonal antibodies. J. Pharmacokinet. Pharmacodyn., 43, 427–446 (2016).
• 33) FDA. 2009. “Raxibacumab.”: ‹http://www.fda.gov/downloads/AdvisoryCommittees/CommitteesMeetingMaterials/Drugs/Anti-InfectiveDrugsAdvisoryCommittee/UCM187312.pdf#search=%27raxibacumab+fda+hgs1021%27›, accessed 5 January, 2017.
• 34) Fracasso PM, Burris H 3rd, Arquette MA, Govindan R, Gao F, Wright LP, Goodner SA, Greco FA, Jones SF, Willcut N, Chodkiewicz C, Pathak A, Springett GM, Simon GR, Sullivan DM, Marcelpoil R, Mayfield SD, Mauro D, Garrett CR. A phase 1 escalating single-dose and weekly fixed-dose study of cetuximab: pharmacokinetic and pharmacodynamic rationale for dosing. Clin. Cancer Res., 13, 986–993 (2007).
• 35) Mentré F, Kovarik J, Gerbeau C. Constructing a prediction interval for time to reach a threshold concentration based on a population pharmacokinetic analysis: an application to basiliximab in renal transplantation. J. Pharmacokinet. Biopharm., 27, 213–230 (1999).
• 36) Puchalski T, Prabhakar U, Jiao Q, Berns B, Davis HM. Pharmacokinetic and pharmacodynamic modeling of an anti-interleukin-6 chimeric monoclonal antibody (siltuximab) in patients with metastatic renal cell carcinoma. Clin. Cancer Res., 16, 1652–1661 (2010).
• 37) Xu Z, Seitz K, Fasanmade A, Ford J, Williamson P, Xu W, Davis HM, Zhou H. Population pharmacokinetics of infliximab in patients with ankylosing spondylitis. J. Clin. Pharmacol., 48, 681–695 (2008).
• 38) van Hartingsveldt B, Nnane IP, Bouman-Thio E, Loza MJ, Piantone A, Davis HM, Petty KJ. Safety, tolerability and pharmacokinetics of a human anti-interleukin-13 monoclonal antibody (CNTO 5825) in an ascending single-dose first-in-human study. Br. J. Clin. Pharmacol., 75, 1289–1298 (2013).
• 39) PMDA. 2015. “Ramucirumab (Cyramza).”: ‹http://www.pmda.go.jp/drugs/2015/P201500028/index.html›, accessed 5 January, 2017.
• 40) Agus DB, Gordon MS, Taylor C, Natale RB, Karlan B, Mendelson DS, Press MF, Allison DE, Sliwkowski MX, Lieberman G, Kelsey SM, Fyfe G. Phase I clinical study of pertuzumab, a novel HER dimerization inhibitor, in patients with advanced cancer. J. Clin. Oncol., 23, 2534–2543 (2005).
• 41) Tokuda Y, Watanabe T, Omuro Y, Ando M, Katsumata N, Okumura A, Ohta M, Fujii H, Sasaki Y, Niwa T, Tajima T. Dose escalation and pharmacokinetic study of a humanized anti-HER2 monoclonal antibody in patients with HER2/neu-overexpressing metastatic breast cancer. Br. J. Cancer, 81, 1419–1425 (1999).
• 42) PMDA. 2007. “Bevacizumab (Avastin).”: ‹http://www.pmda.go.jp/drugs/2007/P200700027/index.html›, accessed 5 January, 2017.
• 43) FDA. 2011. “Belimumab (Benlysta).”: ‹http://www.accessdata.fda.gov/drugsatfda_docs/nda/2011/125370Orig1s000TOC.cfm›, accessed 5 January, 2017.
• 44) PMDA. 2014. “Nivolumab (Opdivo).”: ‹http://www.pmda.go.jp/drugs/2014/P201400114/index.html›, accessed 5 January, 2017.
• 45) FDA. 2004. “Natalizumab (Tysabri).”: ‹http://www.accessdata.fda.gov/drugsatfda_docs/nda/2004/125104s000_Natalizumab.cfm›, accessed 5 January, 2017.
• 46) Smith DA, Minthorn EA, Beerahee M. Pharmacokinetics and pharmacodynamics of mepolizumab, an anti-interleukin-5 monoclonal antibody. Clin. Pharmacokinet., 50, 215–227 (2011).
• 47) Robbie GJ, Criste R, Dall’acqua WF, Jensen K, Patel NK, Losonsky GA, Griffin MP. A novel investigational Fc-modified humanized monoclonal antibody, motavizumab-YTE, has an extended half-life in healthy adults. Antimicrob. Agents Chemother., 57, 6147–6153 (2013).
• 48) Rowinsky EK, Schwartz GH, Gollob JA, Thompson JA, Vogelzang NJ, Figlin R, Bukowski R, Haas N, Lockbaum P, Li YP, Arends R, Foon KA, Schwab G, Dutcher J. Safety, pharmacokinetics, and activity of ABX-EGF, a fully human anti-epidermal growth factor receptor monoclonal antibody in patients with metastatic renal cell cancer. J. Clin. Oncol., 22, 3003–3015 (2004).
• 49) PMDA. 2002. “Palivizumab (Synagis).”: ‹http://www.pmda.go.jp/drugs/2002/P200200010/index.html›, accessed 5 January, 2017.
• 50) Bauer RJ, Dedrick RL, White ML, Murray MJ, Garovoy MR. Population pharmacokinetics and pharmacodynamics of the anti-CD11a antibody hu1124 in human subjects with psoriasis. J. Pharmacokinet. Biopharm., 27, 397–420 (1999).
• 51) Stephens S, Emtage S, Vetterlein O, Chaplin L, Bebbington C, Nesbitt A, Sopwith M, Athwal D, Novak C, Bodmer M. Comprehensive pharmacokinetics of a humanized antibody and analysis of residual anti-idiotypic responses. Immunology, 85, 668–674 (1995).
• 52) Chakraborty A, Tannenbaum S, Rordorf C, Lowe PJ, Floch D, Gram H, Roy S. Pharmacokinetic and pharmacodynamic properties of canakinumab, a human anti-interleukin-1β monoclonal antibody. Clin. Pharmacokinet., 51, e1–e18 (2012).
• 53) FDA. 2013. “Vedolizumab (Entyvio).”: ‹http://www.accessdata.fda.gov/drugsatfda_docs/nda/2011/125370Orig1s000TOC.cfm›, accessed 5 January, 2017.
• 54) Ribas A, Camacho LH, Lopez-Berestein G, Pavlov D, Bulanhagui CA, Millham R, Comin-Anduix B, Reuben JM, Seja E, Parker CA, Sharma A, Glaspy JA, Gomez-Navarro J. Antitumor activity in melanoma and anti-self responses in a phase I trial with the anti-cytotoxic T lymphocyte-associated antigen 4 monoclonal antibody CP-675,206. J. Clin. Oncol., 23, 8968–8977 (2005).
• 55) PMDA. 2008. Adalimumab (Humira). ‹http://www.pmda.go.jp/drugs/2008/P200800019/index.html›, accessed 5 January, 2017.
• 56) Wang W, Wang X, Doddareddy R, Fink D, McIntosh T, Davis HM, Zhou H. Mechanistic pharmacokinetic/target engagement/pharmacodynamic (PK/TE/PD) modeling in deciphering interplay between a monoclonal antibody and its soluble target in cynomolgus monkeys. AAPS J., 16, 129–139 (2014).
• 57) PMDA. 2013. “Pertuzumab (Perjeta).”: ‹http://www.pmda.go.jp/drugs/2013/P201300075/index.html›, accessed 5 January, 2017.
• 58) Halpern WG, Lappin P, Zanardi T, Cai W, Corcoran M, Zhong J, Baker KP. Chronic administration of belimumab, a BLyS antagonist, decreases tissue and peripheral blood B-lymphocyte populations in cynomolgus monkeys: pharmacokinetic, pharmacodynamic, and toxicologic effects. Toxicol. Sci., 91, 586–599 (2006).
• 59) Zia-Amirhosseini P, Minthorn E, Benincosa LJ, Hart TK, Hottenstein CS, Tobia LA, Davis CB. Pharmacokinetics and pharmacodynamics of SB-240563, a humanized monoclonal antibody directed to human interleukin-5, in monkeys. J. Pharmacol. Exp. Ther., 291, 1060–1067 (1999).
• 60) Dall’Acqua WF, Kiener PA, Wu H. Properties of human IgG1s engineered for enhanced binding to the neonatal Fc receptor (FcRn). J. Biol. Chem., 281, 23514–23524 (2006).
• 61) PMDA. 2010. “Panitumumab (Vectibix).”: ‹http://www.pmda.go.jp/drugs/2010/P201000024/index.html›, accessed 5 January, 2017.
• 62) PMDA. 2002. “Basiliximab (Simulect).”: ‹http://www.pmda.go.jp/drugs/2002/P200200005/index.html›, accessed 5 January, 2017.
• 63) PMDA. 2001. “Trastuzumab (Herceptin). ‹http://www.pmda.go.jp/drugs/2001/P200100003/index.html›, accessed 5 January, 2017.
• 64) “Guideline on bioanalytical method validation. 2011.”: ‹http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2011/08/WC500109686.pdf#search=%27guideline+bioanalytical+validation+july+2011%27›.
• 65) Davies B, Morris T. Physiological parameters in laboratory animals and humans. Pharm. Res., 10, 1093–1095 (1993).
• 66) Canadian Council on Animal Care. “Categories of Invasiveness in Animal Experiments.”: ‹https://www.ccac.ca/Documents/Standards/Policies/Categories_of_invasiveness.pdf›, accessed 16 January, 2020.
• 67) Julg B, Sok D, Schmidt SD, Abbink P, Newman RM, Broge T, Linde C, Nkolola J, Le K, Su D, Torabi J, Pack M, Pegu A, Allen MT, Mascola RJ, Burton RD, Barouch HD. Protective efficacy of broadly neutralizing antibodies with incomplete neutralization activity against simian-human immunodeficiency virus in rhesus monkeys. J. Virol., 91, e01187–e17 (2017).
• 68) Komocsar WJ, Blackbourne JL, Halstead CA, Winstead CJ, Wierda D. Fully human anti-BAFF inhibitory monoclonal antibody tabalumab does not adversely affect T-dependent antibody responses in cynomolgus monkey (Macaca fasicularis): A summary of three pre-clinical immunotoxicology evaluations. J. Immunotoxicol., 13, 7–19 (2016).
• 69) Pai R, Ma N, Connor AV, Danilenko DM, Tarrant JM, Salvail D, Wong L, Hartley PD, Misner D, Stefanich E, Wu Y, Chen Y, Wang H, Dambach MD. Therapeutic antibody-induced vascular toxicity due to off-target activation of nitric oxide in cynomolgus monkeys. Toxicol. Sci., 151, 245–260 (2016).
• 70) Schlothauer T, Rueger P, Stracke JO, Hertenberger H, Fingas F, Kling L, Emrich T, Drabner G, Seeber S, Auer J, Koch S, Papadimitriou A. Analytical FcRn affinity chromatography for functional characterization of monoclonal antibodies. MAbs, 5, 576–586 (2013).
• 71) Schoch A, Kettenberger H, Mundigl O, Winter G, Engert J, Heinrich J, Emrich T. Charge-mediated influence of the antibody variable domain on FcRn-dependent pharmacokinetics. Proc. Natl. Acad. Sci. U.S.A., 112, 5997–6002 (2015).
• 72) Kraft TE, Richter WF, Emrich T, Knaupp A, Schuster M, Wolfert A, Kettenberger H. Heparin chromatography as an in vitro predictor for antibody clearance rate through pinocytosis. MAbs, 12, e1683432 (2020).