2015 Volume 21 Issue 3 Pages 291-295
Steam infusion is a pasteurization method used for liquid food such as milk. As the first step in the optimization of the flow rate of milk in the steam infusion chamber, two computational fluid dynamics (CFD) simulations predicted droplet generation from injection water into air and an experiment was carried out. Model 1 only consisted of a nozzle and a region of air. Model 2 consisted of a nozzle, a stainless steel pipe and a region of air. These results were evaluated by the breakup length and projected area. The breakup lengths in the experiment, Model 1 and Model 2 were 94.0 mm, 254.6 mm and 92.1 mm, respectively. The breakup length in Model 1 differed from the experimental data. The projected area in the experiment and Model 2 was 524.5 mm2 and 536.6 mm2, respectively. Both results for Model 2 agreed with the experimental results. Model 2 successfully expressed droplet generation.
Sterilization is one of the most important processes in the food processing industry. The long time low temperature method (LTLT method), the high temperature short time method (HTST method) and the ultra-high temperature method (UHT method) are mainly used in pasteurization processes for liquid food such as milk. LTLT, HTST and UHT methods heat the food for 30 min at about 65°C, for 15 seconds at about 75°C and for 1 – 3 seconds at about 120 – 150°C, respectively. Recently, the UHT method has become popular and can be grouped into indirect and direct heating methods (Uenogawa et al., 2009). There are two methods for direct heating: steam injection, which directly injects steam into liquid food and steam infusion, in which liquid food falls through steam. We focused on milk and steam infusion, which is mainly used in Japan.
The steam applied for steam infusion is heated to 135°C and the temperature of the milk is raised by condensation heat transfer between the steam and milk. This method can pasteurize continuously as well as process a large quantity of milk. This can inhibit heating-related decreases in milk quality because the treatment time is about 1 – 3 seconds (Hayashi et al., 2004). By optimizing the flow rate of milk in the steam infusion chamber, pasteurization efficiency increases.
To optimize the flow rate in the chamber, we have to determine the heat transfer between milk and steam. However, it is difficult to measure the heat transfer by experimental methods and it is almost impossible to measure under various experimental conditions. In recent years, high-performance software has been developed to predict heat transfer and fluid flow correctly. Adachi et al. (2005) predicted the heat transfer and free boundary of a heat exchanger using a computational fluid dynamics (CFD) approach. Piscia et al. (2012) predicted the condensation heat transfer of a greenhouse at night by CFD modeling. Yamamoto et al. (2007) predicted droplet formation by the breakdown of a two-phase jet ejected into air using the volume of fluid (VOF) method. In previous research into steam infusion chambers, Otsuji et al. (2007) predicted the heat transfer and mass transfer between milk and steam, considering that milk falls through the chamber as cylinders and spheres. However, the form did not emulate a real liquid drop precisely. The milk droplet form affects the heat transfer between milk and steam (Isshiki et al., 1984). Therefore, in order to predict correctly the phenomenon of heat transfer in a steam infusion chamber, it is important to identify the precise form of milk. As the first step to identify changes of milk form in the steam, the simulation of droplet generation from injected water into air was carried out.
Experimental apparatus Figure 1(a) shows the outline of the experimental apparatus. Water pooled in a balance tank (F) was raised through a stainless steel pipe (B) by a centrifugal pump (YFP-S177MF1-145; YASUDA FINETECH, Chiba, Japan) (E) and passed through a one-hole nozzle (A). The flow rate of water was adjusted by a needle valve (UN3-BP; KITZ, Chiba, Japan) (C) and measured by a flow meter (FD-SS20A; KEYENCE, Osaka, Japan) (D). Figure 1(b) shows a cross section of the one-hole nozzle. The diameter of the stainless steel nozzle (2.3 mm) was the same as that of the existing equipment.
Outline of the experimental apparatus
Cross section of the one-hole nozzle
Experimental method Water flowed through the nozzle into air at a rate of 50 L h−1 and the appearance of the flow was recorded by a high-speed digital camera (FASTCAM SA5; Photron Inc., Tokyo, Japan). The high-speed camera was placed in front of the water flowing from the nozzle and the water was lit from behind a white screen to unify the background. The distance between the camera and water was 50 mm. The shutter speed was set to 1.0 × 10−4 s and the pixel size was 0.03 × 0.03 mm. From the pictures obtained, changes of the column and droplet shape were analyzed and the breakup length was measured using image-processing software (FASTCAM viewer 3; Photron Inc.). The breakup length is the distance between the nozzle and the head of the liquid column.
Volume of fluid method CFD analysis was carried out using CFD software (ANSYS Fluent 13.0; ANSYS Inc., Canonsburg, PA, USA). The VOF method (Hirt et al., 1981) was used to solve the two-phase flow consisting of water and air. The interface between water and air is tracked by solving a momentum equation, a continuity equation and a volume fraction equation. If the volume fraction of water in the computational cell is denoted as α, these three conditions are possible:
The properties of each cell are determined by the volume fraction of water and air.
Governing equation One momentum equation is solved and shared between two phases as follows:
 |
is the velocity vector, p is pressure, µ is the volume fraction averaged viscosity, 
is the vector of gravitational acceleration and 
is the source term considering surface tension.
Surface tension maintains the balance of the interface and acts only on the surface of the liquid. Namely, the force balances the radially inward molecular attractive force with the radially outward pressure gradient. In regions where two fluids are separated, but one fluid is not in the form of spherical bubbles, the surface tension acts to minimize free energy by decreasing the area of the interface (Fluent Inc., 2006). The continuous surface force (CSF) model (Brackbill et al., 1992) was used as a surface tension model and considered as F in the momentum equation:
 |
To track the interface between liquid food and air, the volume fraction in each cell is determined by solving the volume fraction equation as follows:
 |
 |
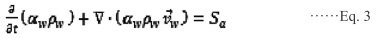The density and viscosity of each control volume are determined by volume fraction. For example, density is defined as:
 |
Geometry Figure 2 shows the outline of the geometry. Two-dimensional geometry was proposed for CFD analysis. Geometry with the exact dimensions of the experimental equipment was created using the ANSYS Design Modeler. Two models were proposed. Model 1 consisted of a nozzle and a region of air and Model 2 consisted of a nozzle, a region of air and a stainless steel pipe. These models show the interior channel of the experimental equipment.
Outline of the geometry used in the simulation
Properties The properties of water and air at 20°C were used for CFD analysis. The density and viscosity of water are 998.2 kg m−3 and 1.003 × 10−3 Pa s, respectively, whereas those of air are 1.225 kg m−3 and 1.789 × 10−5 Pa s, respectively. The coefficient of the surface tension between water and air is set at 7.35 × 10−2 N m−1.
Analysis condition The water flow rate from the inlet and the contact angle were set to 50 L h−1 and 63o, respectively. Gravity acceleration of 9.8 m s−2 was used for all analysis domains in a downward direction. The outlet was defined as an open boundary and static pressure at the outlet was set at 0 Pa. Atmospheric pressure of 1.013 × 105 Pa was set for air. These models were calculated under transient conditions. The time step size for calculation was 1.0 × 10−5 s. The mesh in Model 1 and Model 2 was 99867 and 185348, respectively. First, all the geometry of Model 1 was assembled to be filled with air and the nozzle and stainless steel pipe in Model 2 were filled with water and other regions were filled with air. The computer system employed in the CFD analysis was an Intel (R) Core (TM) i7-2600 (3.40 GHz and 32.0 GB RAM) running Windows 7 Professional SP1 64 bit.
Figure 3 shows images of water flowing from the nozzle used in the experiment. After flowing from the nozzle, the water formed a liquid column. Subsequently, the surface of the liquid column rippled and pinched off. The large droplets pinched off from the liquid column underwent a similar process, forming small droplets. The average breakup length from 20 replications at arbitrary times was 94.0 mm.
Images of water flowing down from the nozzle
Figure 4 shows the results obtained from Model 1. The figure shows the region of air under the nozzle and time passing toward the right. Water formed a liquid column as in the images. The surface of the liquid column then rippled and pinched off. The large droplets pinched off from the liquid column were gradually divided into small droplets. The average breakup length collected from 30 replicates at arbitrary times was 254.6 mm.
Results of simulation of droplet generation in Model 1
Figure 5 shows the results obtained from Model 2. Water droplets were generated similarly to Model 1. Notably, the pattern of water breakup obtained from Model 2 was more precise. The average breakup length collected from 30 replicates at arbitrary times was 92.1 mm.
Results of simulation of droplet generation in Model 2
Comparing the breakup length, Model 1 and the experimental outcome differed by about 160.6 mm, while Model 2 and the experimental outcome differed by only about 1.9 mm. The breakup length of Model 2 agreed well with the experimental outcome. Homma (2003) reported that the breakup length was sensitively affected by the Weber number, as follows:
 |
Next, the projected area of the liquid column and droplets in Model 2 were compared to the area obtained from images in the experiment. These values were the average of 5 replicates at arbitrary times. A region of 50 × 300 mm under the nozzle was cut out and the interface between water and air was extracted by hand. The figures were then uploaded to image processing software (Image J 1.45s; NIH, Bethesda, MD, USA) and processed to black and white binary images. Finally, the projected area was determined by measuring the black area.
The projected area in the experiment and Model 2 was 524.5 mm2 and 536.6 mm2, respectively. The difference in the projected area was 12.1 mm2. As well as the breakup length, the projected area in the experiment and Model 2 agreed well. From these results, Model 2 successfully expressed the appearance of water breakdown from the nozzle.
To predict droplet generation from liquid food flowing from a nozzle, CFD analysis was compared to an experiment. These results were evaluated by the breakup length and projected area. The breakup length in Model 1 differed from that in the experiment. Because of the difference in flow channel geometry, it caused a difference in the distribution of velocity at the inlet and affected the breakup length. On the other hand, the breakup length in Model 2 agreed with the result of the experiment. In addition, the projected area in Model 2 and the experiment agreed well. From these results, Model 2 successfully expressed the shape of water flowing from the nozzle. We expect that by combining a condensation heat transfer model with this CFD model, it will be capable of predicting heat transfer correctly between liquid food and steam. Considering changes in shape, the condensation heat transfer model will make it possible to propose efficient pasteurization conditions.
