2025 年 23 巻 p. 22-65
2025 年 23 巻 p. 22-65
2次ガウシアンモデルに基づく金利期間構造モデルは,下限金利を持つショートレートモデルであり,債券価格のボラティリティ変動を表現するだけでなく,金融危機後に先進国でみられた超低金利イールドカーブを表現する柔軟性を備えている.本研究では,2次ガウシアンモデルを債券と株式に適用し,多通貨市場での債券・株式の同時価格付けモデルを構築する.そのうえで,投資期間に応じた債券や株式のリスクプレミアムと解釈される債券のタームプレミアムと株式のフォワードイールドの解析表現を導出する.また,日米の市場データを用いたモデルの推定を行い,推定値が観測値と高い適合度を示すことを確認するほか,債券のタームプレミアムや株式のフォワードイールドの計測値と景気循環との関係が,先行研究で得られている性質と整合的であることを示す.さらに,日米の金融資産価格に影響を与える共通変数と各国の資産価格のみに影響を与える固有変数が,債券や株式のリスクプレミアムにどのような影響を与えているのかを定量的に明らかにする.
金融資産のリスクプレミアムは,投資家がリスクを取る対価として追加的に要求する収益率を指す.投資期間に応じたリスクプレミアムを計測することは,資産のリスク特性をより深く理解するうえで重要である.本研究では,債券と株式のリスクプレミアムの期間構造を分析するための無裁定価格付けモデルを構築し,市場データに基づくモデルの推定値から,債券や株式のリスクプレミアムの期間構造を計測し,その性質を明らかにする.
債券の投資期間に応じたリスクプレミアムは,一般に「タームプレミアム」として認識される.タームプレミアムは,特定の年限の割引債を購入し満期まで保有することで得られる投資利回りと,短期割引債を繰り返し投資して得られる投資利回りの期待値の差として定義される.
先行研究では,Duffie and Kan (1996)により提案されたアフィンガウシアン金利期間構造モデル(以下,AGモデル)が,タームプレミアムの推定に多く用いられている(例えば,Kim and Wright (2005), Kim and Orphanides (2012), Adrian et al. (2013a), Adrian et al. (2013b), Joslin et al. (2014)).しかし,標準的なAGモデルは金利のボラティリティが一定であると仮定されているため,現実の金利の確率変動を十分に捉えられない.また,先行きの金利が従う確率分布が正規分布と仮定されるため,2008年の世界金融危機以降の先進国のマイナス金利やゼロ金利を含むイールドカーブの表現には限界がある.そこで,近年ではAGモデルに代わるモデルが使われるようになってきている.例えば,Black (1995)が提案し,Gorovoi and Linetsky (2004)により理論が整理された「シャドーレートモデル」,Dai and Singleton (2000)による平方根過程に基づく「平方根過程モデル1」,Ahn et al. (2002)やLeippold and Wu (2003)による「2次ガウシアンモデル」などである.
シャドーレートモデルにより債券のタームプレミアムの推定を行った研究として,Christensen and Rudebusch (2016)やPriebsch (2017)がある.Christensen and Rudebusch (2016)は,米国債金利のゼロ制約が,シャドーレートモデルに基づくタームプレミアムの推定に影響があるか否かを検証している.Priebsch (2017)は,米国の短期の年限のタームプレミアムの変動が比較的大きなことや,1990年以降低下トレンドにあることなどを明らかにしている.Berardi (2023)は,平方根過程モデルを用いて,欧州各国の国債金利のタームプレミアムがグローバルな期待インフレやGDP成長率の正のショックに対して低下することを示している.Chung et al. (2017)は,2次ガウシアンモデルを用いて,米国金利のタームプレミアムが反景気循環的な動きを示すことを明らかにしている.
株式のリスクプレミアムの期間構造に関する研究は,比較的新しい分野である.関連する先行研究では,「配当ストリップス」と呼ばれる仮想的な証券を考え,その現在価値に基づき「株式のゼロクーポンイールド」を定義している.Binsbergen et al. (2012),Binsbergen et al. (2013),Binsbergen and Koijen (2017)は,配当ストリップスの満期までの期間に対応するリスクプレミアムを,株式のゼロクーポンイールドと配当の成長率の期待値の和から実質債券のゼロクーポンイールドを控除した値と定義している.そのうえで,市場データを用いて株式のリスクプレミアムの期間構造を計測し,短期のリスクプレミアムが長期のリスクプレミアムよりも高い値を取ることを明らかにしている.投資期間が長期になると価格変動の不確実性が増すため,長期のリスクプレミアムが短期よりも大きくなることが予想されるが,Binsbergenらの一連の研究はこれを否定する「パズル」として注目され,この分野の研究を活発化させている2.
株式のリスクプレミアムの期間構造に関する先行研究は,Binsbergenらの研究の他,Belo et al. (2015),Breugem and Marf´e (2020), Bansal et al. (2021),Gon¸calves (2021),Gormsen (2021), Takamizawa (2022), Breugem et al. (2023),Hasler and Khapko (2023),Giglio et al. (2024),Suzuki (2024)などが挙げられるが,その多くは代表的個人の効用関数に基づく均衡アプローチを取っている3.例えば,Bansal et al. (2021)は,Bansal and Yaron (2004)の長期リスクモデルに,経済状態に応じてドリフト項が変化する配当成長率の確率過程を組み込んだ拡張を行ったモデルを提案し,当該モデルによって株式のフォワードイールド(株式と債券のゼロクーポンイールドの差)の長短スプレッドが景気後退時に負になることなどを明らかにしている.
株式リスクプレミアムの期間構造の研究で主に採用されている均衡アプローチの利点は,経済理論と直接的に紐づいた形で結果の解釈ができる点にある.一方で,現実の資産価格の特性を単純化した仮定が置かれる場合が多く,モデルの市場価格への適合度が十分とはいえない場合がある.その点,誘導型モデルは市場価格の特性を柔軟に表現できる利点がある.本研究では,市場価格の特性を捉える誘導型の資産価格モデルにより,債券と株式のリスクプレミアムの期間構造を計測する.
債券と株式の価格を統一的な枠組みで評価する誘導型モデルとして,Mamaysky (2002),Lettau and Wachter (2007),Lettau and Wachter (2011)があるが,いずれもAGモデルに基づいている.AGモデルは計算上取り扱いやすいものの,世界金融危機の後に一時期みられた超低金利のイールドカーブを捉えるには限界がある.Kikuchi (2016)は,2次ガウシアンモデルに基づき,債券と株式の同時価格付けモデルを構築し,市場データを用いた実証分析を行っている.同研究では,下限金利を持つ金利期間構造モデルの下,株式指数の配当額を状態変数のある種の関数に設定することで,金利期間構造モデルと整合的な株価の解析表現を得ている4.超低金利環境および資産価格のボラティリティ変動を捉えることができるため,本研究の問題意識に適っている.そこで,Kikuchi (2016)で提案されたモデルを本研究の資産価格モデル構築の軸に据える.
ただし,Kikuchi (2016)のモデルは2次ガウシアンモデルに基づくものであるため,価格や金利が状態変数の非線形関数となる.そのため,結果の解釈が容易ではないという問題がある.この点を改善するため,本研究では,リスクプレミアムが国内市場のみならず国際的な市場連動性に伴い変動する点に着目したモデル化を図る.具体的には,複数通貨を同時に扱うモデルを想定し,資産価格を決定する状態変数を各国の資産価格に共通に影響を与える「国内外共通要因」と1国の資産価格のみに影響を与える「国固有要因」に峻別する.これにより,債券や株式のリスクプレミアムの計測値を「国内外共通要因」からの寄与と「国固有要因」からの寄与に分解して解釈できるようになる.
本研究のモデル構築にあたって,単一通貨モデルであるKikuchi (2016)に,2次ガウシアンモデルに基づき複数通貨の金利と為替の同時モデルを構築しているLeippold and Wu (2007)の設定を組み込む.それにより,2次ガウシアンモデルに基づく多通貨の債券と株式価格の同時モデルを構築する.このように構築されるモデルは,Leippold and Wu (2007)で提案されたモデルから為替レートを取り除き,各国の株価や配当を組み込んだ枠組みとみることができる.
本研究の貢献をあらかじめまとめると,次の3点が挙げられる.まず,本研究は,2次ガウシアンモデルに基づき,多通貨建ての債券・株式の同時価格付けモデルを構築し,その下で配当ストリップスの価格付け公式を導出している点である.2次ガウシアンモデルに基づく配当ストリップスの価格付け公式はこれまでの研究では得られていない新たな成果であり,この公式により,株式リスクプレミアムの期間構造を現実の市場価格の特性に即して分析することが可能になる.第2に,本研究では,提案モデルを推定し,債券のタームプレミアムや株式のリスクプレミアムの期間構造において先行研究で得られている知見と整合的な結果を得た点であり,実証面での貢献の1つである.第3に,本研究は,資産価格を決定する状態変数を「国内外共通要因」と「各国固有要因」に分けてモデルに導入し,債券および株式のリスクプレミアムに対するこれらの要因の寄与を定量化している点である.この方法は,非線形モデルに基づく実証研究で生じうる解釈の困難性を克服する方法論の一例を提示するものである.
本論文の構成は次の通りである.2節では債券と株式の価格,ならびに債券のタームプレミアムや株式のリスクプレミアムについての解析表現を得るための理論を説明する.3節ではモデルの推定に向けた様々な設定を示す.4節では,モデルの推定結果,推定値に基づく債券のタームプレミアム,株式のゼロクーポンイールドやリスクプレミアムの計測や要因分解の結果を示す.5節では,本論文のまとめと今後の課題を記す.
本小節で,モデルの準備をする.フィルター付き確率空間を$(\Omega, \mathcal{F}, (\mathcal{F}_t)_{0 \leqq t}, \mathbb{P})$とし,フィルター$(\mathcal{F}_t)_{0 \leqq t}$は完備で右連続な通常の条件を満たすとする.ここで,$\mathbb{P}$は現実確率を表すとする.$m$か国の金融市場が存在し,各国は自身の通貨と債券を発行しているとする.各国金融市場は完備と仮定する.この仮定により,第$j$国の金融市場について,$\mathbb{P}$と同値なリスク中立確率測度$\mathbb{Q}^j$が唯一つ存在する.$W_{t} \in \mathbb{R}^{\ell}$は,$\mathcal{F}_t$に適合する$\mathbb{P}$上の標準ブラウン運動とする.なお,以下では,行列(ベクトル)$A'$は$A$の転置行列(ベクトル)を表すこととする.また,正方行列$A$に対して,$\mathrm{Tr}(A)$は$A$の対角和を表すこととする.
各国の金利や株価に影響を与える状態変数$X_{t}$を導入する.$X_{t} \in \mathbb{R}^{\ell}$は,次のオルンシュタイン=ウーレンベック過程に従うとする.
| $$dX_{t} = K (\theta-X_{t})dt + \Sigma dW_{t}. $$ | (1) |
ここで,$K \in \mathbb{R}^{\ell \times \ell}$,$\theta \in \mathbb{R}^{\ell}$,$\Sigma \in \mathbb{R}^{\ell \times \ell}$である.$K$については,全ての固有値が正の値を取ると仮定する.この仮定により,$X_{t}$は定常過程となる.また,$\Sigma \Sigma'$は正定値行列であると仮定する.以上の仮定の下,$X_{t}$が市場で直接観測されない潜在変数である場合に付録Dで説明する「不変変換」が適用できる.$X_{t}$が潜在変数の場合,不変変換により式(1)の$K$は対角成分が全て正である下三角行列,$\theta$は零ベクトル,$\Sigma$は単位行列に変換できる.
第$j$国のショートレート$r_{t}^{j}$は,次のように$X_t$の2次関数で定義されるとする.
| $$r_{t}^{j}=X_{t}' \Psi^{j} X_{t} + \varphi^{j \prime} X_t + \eta^{j}, $$ | (2) |
ここで,$\Psi^{j} \in \mathbb{R}^{\ell \times \ell}$,$\varphi^{j} \in \mathbb{R}^{\ell}$,$\eta^{j} \in \mathbb{R}$である.また,$\Psi^{j}$は正定値対称行列と仮定する.この仮定により$r_{t}^{j}$は下限を持つ.以上の設定は,Ahn et al. (2002)やLeippold and Wu (2003)で研究された「2次ガウシアン金利期間構造モデル」の基本的な設定である.
第$j$国のリスク中立確率測度の現実確率に対するラドン=ニコディム微分を$\mathcal{R}^{j} = \displaystyle \frac{d \mathbb{Q}^{j}}{d \mathbb{P}}$と置く.$\mathcal{R}^{j}$について,ノビコフ条件を満たす適合過程$\Lambda_{t}^{j} \in \mathbb{R}^{\ell}$が存在して,次式を満たすとする.
| $$\mathcal{R}_{t}^{j} = \exp \left(- \int_{0}^{t} \Lambda_{u}^{j \prime} dW_{u} - \displaystyle \frac{1}{2} \int_{0}^{t} ||\Lambda_{u}^{j}||^{2} du \right).$$ | (3) |
式(3)を用いると,第$j$国の確率割引ファクター$\mathcal{M}_{t}^{j}$は次のようになる.
| $$\mathcal{M}_{t}^{j} = \exp \left(- \int_{0}^{t} r_{s}^{j} ds \right) \mathcal{R}_{t}^{j}.$$ | (4) |
ギルサノフの定理より,第$j$国のリスク中立確率測度$\mathbb{Q}^{j}$の下で標準ブラウン運動$W_{t}^{j} \in \mathbb{R}^{\ell}$が存在し,
| $$W_{t}^{j} = W_{t} + \int_{0}^{t} \Lambda_{u}^{j} du,$$ | (5) |
である.ここで,式(5)の$\Lambda_{t}^{j}$は,Duffee (2002)により導入された「本質的アフィン」に従うと仮定する.すなわち,
| $$\Lambda_{t}^{j}=\lambda^{j} + \Lambda^{j} X_{t},$$ | (6) |
と仮定する.ここで,$\lambda^{j} \in \mathbb{R}^{\ell}$,$\Lambda^{j} \in \mathbb{R}^{\ell \times \ell}$である.
$X_{t}$の$\mathbb{Q}^j$の下での確率過程は,式(1), (5), (6)から次式で表される.
| $$\begin{split} dX_{t} &= K^{j} (\theta^{j}-X_{t}) dt+ \Sigma dW_{t}^{j}, \\ K^{j} &= K + \Sigma \Lambda^{j}, \ \ K^{j} \theta^{j} =K \theta - \Sigma \lambda^{j}. \end{split}$$ | (7) |
2,1節での設定に基づく割引債価格の解析表現はAhn et al. (2002),Leippold and Wu (2002),Leippold and Wu (2003),Leippold and Wu (2007)で既に与えられている.本小節では,2.3節以降に必要な記法の準備として割引債価格の解析式を表す.
現在の時刻を$t$,割引債の満期時点を$T$とする.割引債の残存年数を$\tau=T-t$と置く.第$j$国が発行する,残存年数が$\tau$年,額面が第$j$国通貨$1$単位の割引債の時刻$t$での価格を$P_{t}^{\tau, j}$と置く.$P_{t}^{\tau, j}$は次式により計算される.
| $$P_{t}^{\tau, j}=E_{t}^{\mathbb{Q}^j} \left[\exp \left(- \int_{t}^{T} r_{u}^{j} du \right) \right].$$ | (8) |
ここで,$E_{t}^{\mathbb{Q}^{j}}[\ ]$は,$\mathbb{Q}^{j}$の下での時刻$t$における条件付期待値オペレータを表す.
$P_{t}^{\tau, j}$は次の解析表現を持つ.証明の概要は付録Aで示す.
| $$P_{t}^{\tau, j}=\exp \left(X_{t}' A_{\tau}^{j} X_{t} + b_{\tau}^{j \prime} X_{t} + c_{\tau}^{j} \right).$$ | (9) |
ここで,式(9)の各係数は次の連立微分方程式の解である.
| $$\begin{split} \displaystyle \frac{d A_{\tau}^{j} }{ d \tau } &= -{K^{j \prime}} A_{\tau}^{j} - A_{\tau}^{j} {K^{j}} + \displaystyle 2 A_{\tau}^{j} \Sigma \Sigma' A_{\tau}^{j} - \Psi^{j}, \ A_{0}^{j}=0_{\ell \times \ell}, \\ \displaystyle \frac{d b_{\tau}^{j}}{ d \tau } &= 2A_{\tau}^{j} K^{j} \theta^{j} - K^{j \prime} b_{\tau}^{j} + 2A_{\tau}^{j} \Sigma \Sigma' b_{\tau}^{j} - \varphi^{j}, \ b_{0}^{j}=0_{\ell \times 1}, \\ \displaystyle \frac{d c_{\tau}^{j} }{d \tau } &= (K^{j} \theta^{j})' b_{\tau}^{j} + \displaystyle \frac{1}{2} \mathrm{Tr} (\Sigma \Sigma^{'} (2A_{\tau}^{j} + b_{\tau}^{j} b_{\tau}^{j \prime})) -\eta^{j}, \ c_{0}^{j}=0. \end{split}$$ | (10) |
式(9)に伊藤の公式を適用すると,$P_{t}^{\tau, j}$は現実確率測度$\mathbb{P}$の下で次の確率過程に従うことが分かる.
| $$\dfrac{dP_{t}^{\tau, j}}{P_{t}^{\tau, j}} = \left( r_{t}^{j} + (2A_{\tau}^{j} X_{t} + b_{\tau}^{j})' \Sigma (\Lambda^{j} X_t + \lambda^{j}) \right) dt + (2A_{\tau}^{j} X_{t} + b_{\tau}^{j})' \Sigma dW_{t}.$$ | (11) |
本小節では,債券のゼロクーポンイールドとタームプレミアムの解析表現を導出する.
まず,第$j$国が発行する債券の残存年数$\tau$年ゼロクーポンイールド$by_{t}^{\tau, j}$は,式(9)より,
| $$by_{t}^{\tau, j} = - \dfrac{1}{\tau} \log P_{t}^{\tau, j}=-\dfrac{1}{\tau} \left(X_{t}' A_{\tau}^{j} X_{t} + b_{\tau}^{j \prime} X_{t} + c_{\tau}^{j} \right),$$ | (12) |
と表される.
$\tau$年のタームプレミアムは,$\tau$年ゼロクーポンイールド$by_{t}^{\tau, j}$と,$j$国通貨1単位を銀行預金に$\tau$年預けて運用する際に得られる複利最終利回りの確率測度$\mathbb{P}$での期待値の差として定義される.後者を数式で表すと,
| $$-\dfrac{1}{\tau} \log E_{t}^{\mathbb{P}} \left[\exp \left(- \int_{t}^{T} r_{u}^{j} du \right) \right],$$ | (13) |
である.式(8)の期待値が式(7)の確率過程を用いることにより式(9)(10)のように解析的に表現できることと同様に,式(1)の確率過程を用いることにより式(13)の解析表現を以下のように導出することができる.
| $$-\dfrac{1}{\tau} \log E_{t}^{\mathbb{P}} \left[\exp \left(- \int_{t}^{T} r_{u}^{j} du \right) \right]=-\dfrac{1}{\tau} \left( X_{t}' \tilde{A}_{\tau}^{j} X_{t} + \tilde{b}_{\tau}^{j \prime} X_{t} + \tilde{c}_{\tau}^{j} \right).$$ | (14) |
ここで,$\tilde{A}_{\tau}^{j}$,$\tilde{b}_{\tau}^{j}$,$\tilde{c}_{\tau}^{j}$は次の連立常微分方程式の解である.
| $$\begin{split} \displaystyle \frac{d \tilde{A}_{\tau}^{j} }{ d \tau } &= -K' \tilde{A}_{\tau}^{j} - \tilde{A}_{\tau}^{j} K + \displaystyle 2 \tilde{A}_{\tau}^{j} \Sigma \Sigma' \tilde{A}_{\tau}^{j} - \Psi^{j}, \ \tilde{A}_{0}^{j}=0_{\ell \times \ell}, \\ \displaystyle \frac{d \tilde{b}_{\tau}^{j}}{ d \tau } &= 2 \tilde{A}_{\tau}^{j} K \theta - K' \tilde{b}_{\tau}^{j} + 2 \tilde{A}_{\tau}^{j} \Sigma \Sigma' \tilde{b}_{\tau}^{j} - \varphi^{j}, \ \tilde{b}_{0}^{j}=0_{\ell \times 1}, \\ \displaystyle \frac{d \tilde{c}_{\tau}^{j} }{d \tau } &= (K \theta)' \tilde{b}_{\tau}^{j} + \displaystyle \frac{1}{2} \mathrm{Tr} (\Sigma \Sigma^{'} (2 \tilde{A}_{\tau}^{j} + \tilde{b}_{\tau}^{j} \tilde{b}_{\tau}^{j \prime})) -\eta^{j}, \ \tilde{c}_{0}^{j}=0. \end{split}$$ | (15) |
式(12)(14)より,第$j$国債券の$\tau$年のタームプレミアム$btp_{\tau}^{j}$は,
| $$btp_{\tau}^{j} = \dfrac{1}{\tau} \left( X_{t}' (\tilde{A}_{\tau}^{j} - A_{\tau}^{j}) X_{t} + (\tilde{b}_{\tau}^{j}- b_{\tau}^{j})' X_{t} + \tilde{c}_{\tau}^{j} -c_{\tau}^{j} \right),$$ | (16) |
と表される.
2.4 株価のモデリング本研究において,株価のモデリングはKikuchi (2016)が提案したモデルに従う.本小節では,Kikuchi (2016)により与えられた2次ガウシアンモデルに基づく株価の解析表現に係る定理を示す.同定理の証明の概要は付録Bで説明する.
第$j$国の株式指数は連続的に配当を投資家に支払うものとする. 時刻$t$における瞬間的な配当額$D_{t}^{j}$は次式の関数形を想定する.
| $$D_{t}^{j} = (X_{t}' \Delta^{j} X_{t} + \delta^{j \prime} X_{t} +\delta_{0}^{j}) \exp \left( X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t \right).$$ | (17) |
ここで,$\Delta^{j}$は正定値対称行列と仮定する.
第$j$国の株式指数を$S_{t}^{j}$とする.無裁定条件より,$S_{t}^{j}$は将来の配当流列の$\mathbb{Q}^{j}$の下での期待割引現在価値として定まる.すなわち,以下の式(18)が成り立つ.
| $$S_{t}^{j} = E_{t}^{\mathbb{Q}^j} \left[\int_{t}^{\infty} \exp \left( -\int_{t}^{s} r_{u}^{j} du \right) D_{s}^{j} ds \right].$$ | (18) |
付録Bで示す議論により,式(17)で想定した瞬間的な配当額を定めるパラメータ$E^{j}$,$f^{j}$,$g^{j}$は,以下の連立代数方程式の解として定まることになる.
| $$\begin{split} &2E^{j} \Sigma \Sigma^{\prime} E^{j} - K^{j \prime} E^{j} - E^{j} K^{j} + \Delta^{j} - \Psi^{j} = 0, \\ &-f^{j \prime}(K^{j} - 2 \Sigma\Sigma' E^{j}) + 2 \theta^{j \prime} K^{j \prime} E^{j} + \delta^{j} - \varphi^{j} = 0, \\ &g^{j} + \frac{1}{2} \mathrm{Tr} (\Sigma \Sigma'(2E^{j} + f^{j} f^{j \prime}))+ f^{j \prime} K^{j} \theta^{j} + \delta_{0}^{j} -\eta^{j} =0. \label{eq:algebra} \end{split}$$ | (19) |
式(18)における$S_{t}^{j}$の解析表現に関して,以下の定理が成り立つ.
定理1.$\Delta^j$,$\Psi^j - \Delta^j$は正定値対称行列とする.また,$\delta_{0}^{j} = \frac{1}{4} \delta^{j \prime} {\Delta^{j}}^{-1} \delta^{j}$とする.ここで,連続的な支払いを行う株式の瞬間的な配当額が式(17)の関数形で与えられる場合,式(18)の右辺で定義される株価$S_{t}^{j}$は次の形に定まる.
| $$S_{t}^{j} = \exp \left( X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t \right).$$ | (20) |
ここで,式(20)の$E^{j}$,$f^{j}$,$g^{j}$は式(19)の連立代数方程式の解である.式(20)において$E^{j}$を正定値対称行列とする株価の解析表現が存在し,一意に定まる.
定理1の証明の概略は付録Bに記す.
モデルのパラメータが定理1の条件を満たすとする.このとき,$\delta_{0}^{j} = \frac{1}{4} \delta^{j \prime} {\Delta^{j}}^{-1} \delta^{j}$より,配当利回りは,
| $$\dfrac{D_{t}^{j}}{S_{t}^{j}} = X_{t}' \Delta^{j} X_{t} + \delta^{j \prime} X_{t} +\delta_{0}^{j}= \left(X_{t}+\dfrac{1}{2} {\Delta^{j}}^{-1} \delta^{j} \right)' \Delta^{j} \left(X_{t}+\dfrac{1}{2} {\Delta^{j}}^{-1} \delta^{j} \right),$$ | (21) |
となる.今,$\Delta^{j}$は正定値対称行列と仮定しているので,配当利回りは常に非負である.
株式指数の現実確率測度$\mathbb{P}$の下での確率過程は,
| $$\dfrac{dS_{t}^{j} + D_{t}^{j} dt}{S_{t}^{j}} = \left( r_{t}^{j} + (2E^{j} X_{t} + f^{j})' \Sigma (\Lambda^{j} X_t + \lambda^{j}) \right) dt + (2E^{j} X_{t} + f^{j})' \Sigma dW_{t},$$ | (22) |
となる.
2.5 株式のゼロクーポンイールド/リスクプレミアムBinsbergen et al. (2012)のほか,株式の利回りやリスクプレミアムの期間構造に関する先行研究では,配当ストリップスと呼ばれる金融契約の現在価値が大きな役割を果たす.本小節では,配当ストリップスの現在価値の解析表現を与える定理を導き, 株式の利回りやリスクプレミアムの期間構造に係る解析式を示す.
満期を$T$とする配当ストリップスは,$T$で配当$D_{T}$を受け取る金融契約である. 第$j$国の株式指数の配当を対象とする残存年数$\tau$年の配当ストリップスの時刻$t$での価格を$DSS_{t}^{\tau, j}$とすると,$DSS_{t}^{\tau, j}$は次式で与えられる.
| $$DSS_{t}^{\tau, j} = E_{t}^{\mathbb{Q}^j} \left[\exp\left(-\int_{t}^{t+\tau}r_{u}^{j} du \right) D_{t+\tau}^{j} \right].$$ | (23) |
株式の瞬間的な配当額が式(17)に従う場合,$DSS_{t}^{\tau, j}$の解析表現に関して次の定理が成り立つ.
定理2. 株式の瞬間的な配当額が式(17)に従うとする.また,パラメータは定理1の条件を満たすとする.このとき,$DSS_{t}^{\tau, j}$は次の解析表現を持つ.
| $$DSS_{t}^{\tau,j} =- \left(X_{t}' \dfrac{d E_{\tau}^{j}}{d \tau} X_{t} + {\dfrac{d f_{\tau}^{j \prime}}{d \tau}} X_{t} + \dfrac{d h_{\tau}^{j}}{d \tau} \right) \exp(X_{t}' E_{\tau}^{j} X_{t} + {f_{\tau}^{j \prime}} X_{t} + g_{\tau}^{j} t + h_{\tau}^{j}).$$ | (24) |
ここで,右辺の係数は下の連立微分方程式(25)の解である.
| $$\begin{split} \displaystyle \frac{d E_{\tau}^{j} }{ d \tau } &= -K^{j \prime} E_{\tau}^{j} - E_{\tau}^{j} K^{j} + \displaystyle 2 E_{\tau}^{j} \Sigma \Sigma' E_{\tau}^{j} - \Psi^{j}, \ E_{0}^{j}=E^{j}, \\ \displaystyle \frac{d f_{\tau}^{j}}{ d \tau } &= 2E_{\tau}^{j} K^{j} \theta^{j} - {K^{j \prime}} f_{\tau}^{j} + 2E_{\tau}^{j} \Sigma \Sigma' f_{\tau}^{j} - \varphi^{j}, \ f_{0}^{j} = f^{j}, \\ \displaystyle \frac{d h_{\tau}^{j} }{d \tau } &= (K^{j} \theta^{j})' f_{\tau}^{j} + \displaystyle \frac{1}{2} \mathrm{Tr} (\Sigma \Sigma' (2E_{\tau}^{j} + f_{\tau}^{j} f_{\tau}^{j \prime})) +g_{\tau}^{j} - \eta^{j}, \ h_{0}^{j} = 0, \\ g_{\tau}^{j} &=g^{j}. \end{split}$$ | (25) |
ここで,$E^{j}$,$f^{j}$,$g^{j}$は株価を定める式(20)の係数であり,式(19)の解である.
定理2の証明の概略は付録Cで与える.
残存年数$\tau$年,第$j$国株式のゼロクーポンイールド$ey_{t}^{\tau, j}$は,$DSS_{t}^{\tau, j}$を用いて次のように定義される.
| $$ey_{t}^{\tau, j} = -\dfrac{1}{\tau} \log \left( \dfrac{DSS_{t}^{\tau, j}}{D_{t}^{j}} \right).$$ | (26) |
式(26)の$ey_{t}^{\tau, j}$は,配当ストリップスの価格の支払い配当額に対する割引率を表している.
仮に,$\tau$年間の配当の成長率,国債の金利が一定と仮定し,それぞれ年率$gr^{\tau,j}$,$by^{\tau,j}$と置くと,配当ストリップスの価格$DSS_{t}^{\tau,j}$は,リスクプレミアムの年率平均$erp^{\tau,j}$を用いて
| $$DSS_{t}^{\tau,j} = D_{t}^{j} \exp(gr^{\tau,j}\tau)\exp(-(by^{\tau,j}+erp^{\tau,j})\tau),$$ |
となる.この式と式(26)より,
| $$erp^{\tau,j} = ey^{\tau,j} -by^{\tau,j} + gr^{\tau,j},$$ |
となる.
配当の成長率や国債の金利が確率変動する本研究の本来の設定に立ち返っても,上と同様の考え方が適用できる.したがって,株式の$\tau$年のリスクプレミアム$erp_{t}^{\tau, j}$は,次式で与えられる.
| $$erp_{t}^{\tau, j} = ey_{t}^{\tau, j} - by_{t}^{\tau, j} + gr_{t}^{\tau, j}.$$ | (27) |
ここで,$gr_{t}^{\tau, j}$は,時刻$t$から$\tau$年間の配当成長率の期待値の年率平均を表しており,
| $$gr_{t}^{\tau, j} = \dfrac{1}{\tau} E_{t}^{\mathbb{P}} \left[ \log \left( \dfrac{D_{t+\tau}^{j}}{D_{t}^{j}} \right) \right],$$ | (28) |
である.なお,式(27)のリスクプレミアムの定義は,Binsbergen et al. (2013)やBansal et al. (2021)などで広く用いられているものである5.
式(27)のリスクプレミアム$erp_{t}^{\tau, j}$を求める際,$ey_{t}^{\tau,j}$は式(26),$by_{t}^{\tau,j}$は式(12)によって与えられるが,$gr_{t}^{\tau, j}$は式(28)の期待値計算が必要となる.この期待値を計算するにあたり,式(17)の$D_{t}^{j}$の定義に立ち返ると,$E_{t}^{\mathbb{P}}[\log(X_{t+\tau}' \Delta^{j} X_{t+\tau} + \delta^{j \prime} X_{t+\tau} + \delta_{0})]$という解析表現を得ることが難しい項が含まれていることが分かる.ただし,式(28)は解析的に求めることは難しいが,モンテカルロ・シミュレーションを用いることで計算が可能である.3.2節では,パラメータ推定上の識別性を確保するため「不変変換」によってパラメータに一定の制約を課す.この不変変換を適用すると,$\theta$を零ベクトルに,$\Sigma$を単位行列に変換できる.この変換の結果として,
| $$X_{t+\tau} |_{\mathcal{F}_{t}} \sim N\left( e^{-K \tau}X_{t}, \displaystyle \int_{0}^{\tau} e^{-Ks}e^{-K's} ds \right),$$ |
が得られることは,3.3節の式(39)によって示される.この関係式に基づき$X_{t+\tau}$の値を正規乱数によりシミュレーションすることで,$E_{t}^{\mathbb{P}}[\log(X_{t+\tau}' \Delta^{j} X_{t+\tau} + \delta^{j \prime} X_{t+\tau} + \delta_{0})]$など,解析表現を得ることが難しい項も計算することができる.その結果,式(28)の右辺も計算可能であり,得られた結果を式(27)に代入すると$erp_{t}^{\tau,j}$を計算することができる.
以上のように,モンテカルロ・シミュレーションに頼れば,株式リスクプレミアム$erp_{t}^{\tau,j}$を計測することは可能である.しかし,本研究の目的の1つであるリスクプレミアムを「国内外の共通要因」や「国固有の要因」に分解して捉えるには,煩雑な計算が必要になる.そこで,本研究の実証分析においては,株式と債券の同年限のゼロクーポンイールドの差として定義される株式のフォワードイールドを,株式リスクプレミアムの代替指標として計測することにする.すなわち,$\tau$年の株式フォワードイールド$efy_{t}^{\tau,j}$は,
| $$efy_{t}^{\tau, j} = ey_{t}^{\tau, j} - by_{t}^{\tau, j},$$ | (29) |
である.$efy_{t}^{\tau,j}$は,式(27)と(29)より$erp_{t}^{\tau,j}-gr_{t}^{\tau,j}$と等しいことから,フォワードイールドは「配当の成長率を加味しない場合のリスクプレミアム」と解釈できる.
本研究における実証分析において,$efy_{t}^{\tau,j}$に対する「国内外の共通要因」や「国固有の要因」の寄与度を定量化する.そのために,式(26)に式(17),(24)を代入し,式(12)を用いて,$efy_{t}^{\tau,j}$を次のような形で表しておく.
| $$\begin{split} efy_{t}^{\tau, j} &= ey_{t}^{\tau, j} - by_{t}^{\tau, j} \\ &= \dfrac{1}{\tau} \left( X_{t}' (A_{\tau}^{j} - E_{\tau}^{j} +E^{j}) X_{t} + (b_{\tau}^{j}-f_{\tau}^{j} + f^{j})^{\prime} X_{t} + c_{\tau}^{j} - h_{\tau}^{j} \right) \\ &\ \ - \dfrac{1}{\tau} \log \left(- \left(X_{t}' \dfrac{d E_{\tau}^{j}}{d \tau} X_{t} + {\dfrac{d f_{\tau}^{j \prime}}{d \tau}} X_{t} + \dfrac{d h_{\tau}^{j}}{d \tau} \right) \right) + \dfrac{1}{\tau} \log \left(X_{t}' \Delta^{j} X_{t} + \delta^{j \prime} X_{t} + \delta_{0}^{j} \right) \\ &=\dfrac{1}{\tau} \left( X_{t}' (A_{\tau}^{j} - E_{\tau}^{j} +E^{j}) X_{t} + (b_{\tau}^{j}-f_{\tau}^{j} + f^{j})^{\prime} X_{t} \right) \\ &\ \ \ -\dfrac{1}{\tau} \left(X_{t}' \dfrac{\dfrac{d E_{\tau}^{j}}{d \tau}}{\dfrac{d h_{\tau}^{j}}{d \tau}} X_{t} + \dfrac{\dfrac{d f_{\tau}^{j \prime}}{d \tau}}{\dfrac{d h_{\tau}^{j}}{d \tau}} X_{t} \right) +\dfrac{1}{\tau} \left(X_{t}' \dfrac{\Delta^{j}}{\delta_{0}^{j}} X_{t} + \dfrac{\delta^{j \prime}}{\delta_{0}^{j}} X_{t} \right)\\ &\ \ \ + \dfrac{1}{\tau} \left(c_{\tau}^{j} - h_{\tau}^{j} -\log \left( -\dfrac{d h_{\tau}^{j}}{d \tau} \right) + \log \delta_{0}^{j}\right) + error_{t}^{\tau,j}. \end{split}$$ | (30) |
ここで,3つ目の等号では2つ目の等号の右辺に現れる自然対数の項を線形近似している.さらに,3つ目の等号右辺の$error_{t}^{\tau,j}$は自然対数の線形近似に伴う誤差を集約した値を表している.式(30)により,株式フォワードイールドを国内外共通要因と国内固有要因へ分解して捉えることが可能になる.4.3節では,推定値を用いた株式フォワードイールドの要因分解の計測結果を示す.
日本と米国の2か国の金融時系列データに対してモデルの推定を行う.サンプル期間は2000年1月~2019年12月の月次データとする.
金利のデータについては,債券の特定の残存年数のゼロクーポンイールドを用いる.日米とも国債の市場価格から推定された残存年数$0.5$年,$2$年,$5$年,$7$年,$10$年,$20$年のゼロクーポンイールドである.月末最終営業日の債券の市場価格から計算された値を用いる.米国債のゼロクーポンイールドのデータは,“U.S. Treasury Discount Bond Database”(https://www.discount-bond-data.org/home)から取得した.これらの金利データは,Filipovi´c et al. (2022)の研究に基づき,その著者らがカーネルリッジ回帰法を用いて推定したものである.日本国債のゼロクーポンイールドは,日経NEEDS-FinancialQUESTから入手した日本の固定利付国債の価格データから,Steeley (1991)に則りBスプライン基底関数を用いて推定したものを用いる.
株価については,米国はS&P500,日本はTOPIXの月末最終営業日の終値を用いる.S&P500はInvesting.comから,TOPIXはYahoo!ファイナンスから取得した.これらの株式指数の配当利回りの月次データも推定に用いる.TOPIXは日本取引所グループのホームページから,S&P500については,ロバート・シラー教授のホームページ(http://www.econ.yale.edu/~shiller/data.htm)から取得した.
モデルの推定は,金利,株式指数,配当利回りだけでなく,S&P500とTOPIXの月次収益率の分散の時系列値も含めた形で行う.これは,金利期間構造モデルにおける推定において,イールドカーブの時系列データに10年金利のボラティリティを加えて推定を行ったBerardi (2023)の方法を参考にした.株式の収益率の分散のデータとして,株式オプションの価格から得られるインプライド分散のデータが入手可能であればそれを利用することが望ましいが,20年近くの長期にわたるインプライド分散のデータを公開データから入手することは難しい6.そこで本研究では,株価のヒストリカルボラティリティにインプライドボラティリティに関する情報がある程度反映しているとの仮定のもと,日米株式指数の月次収益率のヒストリカル分散をインプライド分散の代替指標として観測値に含めることにする.なお,ヒストリカル分散は,株価の月次変化率の過去12か月分の不偏分散の年率換算値を用いることにする.
モデルの推定に用いる米国のデータの記述統計量を表1に,日本のデータの記述統計量を表2にまとめた.
| 金利 | 株式 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.5年 | 2年 | 5年 | 7年 | 10年 | 20年 | 指数 | 配当利回り | 分散 | |
| 平均値 | 0.0172 | 0.0206 | 0.0275 | 0.0312 | 0.0353 | 0.0413 | 0.00876 | 0.0189 | 0.0209 |
| 標準偏差 | 0.0180 | 0.0169 | 0.0144 | 0.0133 | 0.0126 | 0.0123 | 0.346 | 0.00371 | 0.0181 |
| 最大値 | 0.0627 | 0.0663 | 0.0665 | 0.0663 | 0.0661 | 0.0657 | 0.788 | 0.0360 | 0.0987 |
| 最小値 | 0000340 | 0.00198 | 0.00596 | 0.00962 | 0.0149 | 0.0185 | -0.692 | 0.0111 | 0.0014 |
金利と配当利回りは原計数をもとに計算.株式指数は1999年12月末の指数に対する相対価格の対数変換値.
分散は月次変化率について後方12か月の分散を年率変換した値.
| 金利 | 株式 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.5年 | 2年 | 5年 | 7年 | 10年 | 20年 | 指数 | 配当利回り | 分散 | |
| 平均値 | 0.000679 | 0.00174 | 0.00446 | 0.00667 | 0.00988 | 0.0166 | -0.350 | 0.0159 | 0.0287 |
| 標準偏差 | 0.00209 | 0.00294 | 0.00458 | 0.00549 | 0.00633 | 0.00660 | 0.2711 | 0.00592 | 0.0184 |
| 最大値 | 0.00717 | 0.00998 | 0.0147 | 0.0172 | 0.0198 | 0.0257 | 0.0644 | 0.0301 | 0.0986 |
| 最小値 | -000373 | -0.00317 | -0.00375 | -0.00382 | -0.00284 | 0.000740 | -0.873 | 0.00620 | 0.00369 |
金利と配当利回りは原計数をもとに計算.株式指数は1999年12月末の指数に対する相対価格の対数変換値.
分散は月次変化率について後方12か月の分散を年率変換した値.
米国を「第1国」,日本を「第2国」とする.これ以降,パラメータに付される添え字の$1$は米国に関するものを表し,$2$は日本に関するものを表す場合がある.
本研究のモデルの推定において,状態変数$X_{t}$は市場で直接観測されない潜在変数であると仮定する.Dai and Singleton (2000)は,潜在変数を状態変数に持つアフィン型金利期間構造モデルにおいて,同一の債券価格を導く状態変数とモデルパラメータの組の間の変換を明らかにし,それを「不変変換(invariant transformation)」と呼んだ7.Ahn et al. (2002),Leippold and Wu (2002)は,2次ガウシアン期間構造モデルにおいて,同一の債券価格を導く状態変数とモデルパラメータの組の間の不変変換を論じている.あらかじめ不変変換を施したモデルを考えると,モデルの枠組みは維持したまま,幾つかのパラメータに制約を課すことができ,パラメータ推定における識別可能性を確保することができる.付録Dに,本研究の債券価格と株価を同時に扱う2次ガウシアンモデルにおける不変変換についてまとめた.
付録Dで示す通り,式(1)の$K$は不変変換により,対角成分が正の値を持つ下三角行列に変換することができる.また,$\theta$は零ベクトルに変換することができる.さらに,状態変数$X_{t}$のボラティリティ行列$\Sigma$を単位行列に変換することができる.そこで,$K$を対角成分の値が正の値を持つ下三角行列,$\theta$を零ベクトル,$\Sigma$を単位行列と仮定する.
2か国の金融市場を同時に扱うモデルを推定することになるため,推定すべきモデルのパラメータの数は多くなる.この点を踏まえ,あらかじめパラメータに幾つかの制約を課しておく.
まず,配当利回りを定める式(21)において,定理1の条件を踏まえて,
| $$\delta_{0}^{j} = \frac{1}{4} \delta^{j \prime} {\Delta^{j}}^{-1} \delta^{j} \ \ (j =1, 2),$$ |
と仮定する.この仮定により,配当利回りは常に非負となる.
本研究のモデルは非線形モデルであるため,推定後の解釈性に乏しいという欠点がある.そこで,日米の資産価格に共通の影響を与える共通変数をモデルに導入し,解釈性を向上させる.状態変数$X_{t}$の次元$\ell$について,$\ell = p + q + r$とするとき,$X_{t}'=(X_{t,1}', X_{t,2}', X_{t,3}')$と置き,$X_{t,1}$は$p$次元ベクトルの「日米共通要因」,$X_{t,2}$は$q$次元ベクトルの「米国固有要因」,$X_{t,3}$は$r$次元ベクトルの「日本固有要因」とみなすことができるようなパラメータの設定を以下で与える.
第$j$国のショートレート$r_{t}^{j}$を定める式(2)の係数行列$\Psi^{j}$は下記の形を取ると仮定する.
| $$\Psi^{1} = \left( \begin{array}{ccc} \begin{matrix} \Psi_{1}^{1} & \large{0} & \large{0} \\ \large{0} & \Psi_{2}^{1} & \large{0} \\ \large{0} & \large{0} & \large{0} \end{matrix} \end{array} \right), \ \ \Psi^{2} = \left( \begin{array}{ccc} \begin{matrix} \Psi_{1}^{2} & \large{0} & \large{0} \\ \large{0} & \large{0} & \large{0} \\ \large{0} & \large{0} & \Psi_{3}^{2} \\ \end{matrix} \end{array} \right).$$ | (31) |
ここで,$\Psi_{1}^{1} \in \mathbb{R}^{p \times p}$,$\Psi_{1}^{2} \in \mathbb{R}^{p \times p}$,$\Psi_{2}^{1} \in \mathbb{R}^{q \times q}$,$\Psi_{3}^{2} \in \mathbb{R}^{r \times r}$とする.なお,それぞれ正定値対称行列とする.式(2)では,$\Psi^{j}$を正定値対称行列としていたが,式(31)では,$\Psi^{1}$と$\Psi^{2}$の小行列
| $$\left( \begin{array}{cc} \begin{matrix} \Psi_{1}^{1} & \large{0} \\ \large{0} & \Psi_{2}^{1} \\ \end{matrix} \end{array} \right), \ \ \ \left( \begin{array}{cc} \begin{matrix} \Psi_{1}^{2} & \large{0} \\ \large{0} & \Psi_{3}^{2} \\ \end{matrix} \end{array} \right),$$ |
が正定値対称行列である.
ショートレート$r_{t}^{j}$を定める式(2)の係数ベクトル$\varphi^{j}$は下記の形を取ると仮定する.
| $$\varphi^{1 \prime} = (\varphi^{11 \prime}, \varphi^{12 \prime}, 0_{1 \times r}), \ \ \varphi^{2 \prime} = (\varphi^{21 \prime}, 0_{1 \times q}, \varphi^{22 \prime}).$$ | (32) |
ここで,$\varphi^{1} \in \mathbb{R}^{\ell}$,$\varphi^{2} \in \mathbb{R}^{\ell}$,$\varphi^{11} \in \mathbb{R}^{p}$,$\varphi^{12} \in \mathbb{R}^{q}$,$\varphi^{21} \in \mathbb{R}^{p}$,$\varphi^{22} \in \mathbb{R}^{r}$とする.
第$j$国の株式の配当$D_{t}^{j}$を定める式(17)の係数行列$\Delta^{j}$は下記の形を取ると仮定する.
| $$\Delta^{1} = \left( \begin{array}{ccc} \begin{matrix} \Delta_{1}^{1} & \large{0} & \large{0} \\ \large{0} & \Delta_{2}^{1} & \large{0} \\ \large{0} & \large{0} & \large{0} \end{matrix} \end{array} \right), \ \ \Delta^{2} = \left( \begin{array}{ccc} \begin{matrix} \Delta_{1}^{2} & \large{0} & \large{0} \\ \large{0} & \large{0} & \large{0} \\ \large{0} & \large{0} & \Delta_{3}^{2} \\ \end{matrix} \end{array} \right).$$ | (33) |
ここで,$\Delta_{1}^{1} \in \mathbb{R}^{p \times p}$,$\Delta_{1}^{2} \in \mathbb{R}^{p \times p}$,$\Delta_{2}^{1} \in \mathbb{R}^{q \times q}$,$\Delta_{3}^{2} \in \mathbb{R}^{r \times r}$とする.なお,それぞれ正定値対称行列とする.式(17)では,$\Delta^{j}$を正定値対称行列と仮定したが,式(33)では,$\Delta^{j}$から全ての成分が零である行と列を取り除いた小行列が正定値対称行列である.また,定理1の条件の1つに関連して,$\Psi_{1}^{1}-\Delta_{1}^{1}$,$\Psi_{2}^{1}-\Delta_{2}^{1}$,$\Psi_{1}^{2}-\Delta_{1}^{2}$,$\Psi_{3}^{2}-\Delta_{3}^{2}$は,それぞれ正定値対称行列と仮定する.
$D_{t}^{j}$を定める式(17)の係数ベクトル$\delta^{j}$は下記の形を取ると仮定する.
| $$\delta^{1 \prime} = (\delta^{11 \prime}, \delta^{12 \prime}, 0_{1 \times r}), \ \ \delta^{2 \prime} = (\delta^{21 \prime}, 0_{1 \times q}, \delta^{22 \prime}).$$ | (34) |
ここで,$\delta^{1} \in \mathbb{R}^{\ell}$,$\delta^{2} \in \mathbb{R}^{\ell}$,$\delta^{11} \in \mathbb{R}^{p}$,$\delta^{12} \in \mathbb{R}^{q}$,$\delta^{21} \in \mathbb{R}^{p}$,$\delta^{22} \in \mathbb{R}^{r}$とする.
以上のショートレートと株式の配当に係るパラメータの設定から,状態変数$X_{t,1}$は,時刻$t$における日米両国のショートレートと配当に影響を与え,$X_{t,2}$は米国のショートレートと配当に,$X_{t,3}$は日本のショートレートと配当に影響を与えることが分かる.
式(7)の係数行列$K^{1}$,$K^{2}$は,下記のブロック行列の形を取るという仮定を課す.
| $$K^{1} = \left( \begin{array}{ccc} \begin{matrix} K_{11}^{1} & \large{0} & \large{0} \\ K_{21}^{1} & K_{22}^{1} & \large{0} \\ \large{0} & \large{0} & \large{0} \end{matrix} \end{array} \right), \ \ K^{2} = \left( \begin{array}{ccc} \begin{matrix} K_{11}^{2} & \large{0} & \large{0} \\ \large{0} & \large{0} & \large{0} \\ K_{31}^{2} & \large{0} & K_{33}^{2} \\ \end{matrix} \end{array} \right).$$ | (35) |
ここで,$K_{11}^{1} \in \mathbb{R}^{p \times p}$,$K_{11}^{2} \in \mathbb{R}^{p \times p}$,$K_{21}^{1} \in \mathbb{R}^{q \times p}$,$K_{22}^{1} \in \mathbb{R}^{q \times q}$,$K_{31}^{2} \in \mathbb{R}^{r \times p}$,$K_{33}^{2} \in \mathbb{R}^{r \times r}$とし,$K_{11}^{1}$,$K_{11}^{2}$,$K_{22}^{1}$,$K_{33}^{2}$は対角成分が正の値を取る下三角行列と仮定する.
式(7)の係数ベクトル$\theta^{1}$,$\theta^{2}$は次の形を取ると仮定する.
| $$\theta^{1 \prime} = (\theta^{11 \prime}, \theta^{12 \prime}, 0_{1 \times r}), \ \ \theta^{2 \prime} = (\theta^{21 \prime}, 0_{1 \times q}, \theta^{22 \prime}).$$ | (36) |
ここで,$\theta^{1} \in \mathbb{R}^{\ell}$,$\theta^{2} \in \mathbb{R}^{\ell}$,$\theta^{11} \in \mathbb{R}^{p}$,$\theta^{12} \in \mathbb{R}^{q}$,$\theta^{21} \in \mathbb{R}^{p}$,$\theta^{22} \in \mathbb{R}^{r}$とする.
債券の価格は,式(9)および式(10)から計算されるが,式(31),(32),(35),(36)の仮定から,時刻$t$における米国の債券の価格は$X_{t,1}$と$X_{t,2}$に依存して,$X_{t,3}$に依存しないことが分かる.また,時刻$t$における日本の債券の価格は$X_{t,1}$と$X_{t,3}$に依存して,$X_{t,2}$に依存しないことが分かる.株価は,式(19),(20)から計算されるが,式(31),(32),(33),(34),(35),(36)の仮定から,時刻$t$における米国の株価は$X_{t,1}$と$X_{t,2}$に依存して,$X_{t,3}$に依存しないことが分かる.また,時刻$t$における日本の株価は$X_{t,1}$と$X_{t,3}$に依存して,$X_{t,2}$に依存しないことが分かる.
定理1では,株価の解析表現を定めるためのパラメータに関する十分条件が与えられていた.本小節での仮定が定理1における条件を満たしているかどうかを確認する.まず,$j=1$については,$\Delta^{1}$,$\Psi^{1}-\Delta^{1}$を$1\text{行目} \sim (p+q)\text{行目}$,$1\text{列目} \sim (p+q)\text{列目}$に制限した行列は,いずれも上で置いた仮定により正定値対称行列である.また,上で仮定した通り,$\delta_{0}^{1} = \frac{1}{4} \delta^{1 \prime} {\Delta^{1}}^{-1} \delta^{1}$である.以上より,$j=1$について,定理1におけるパラメータの条件を満たす.$j=2$については,$\Delta^{2}$,$\Psi^{2}-\Delta^{2}$を$1\text{行目} \sim p\text{行目}$,$1\text{列目} \sim p\text{列目}$と$(p+q+1)\text{行目} \sim (p+q+r)\text{行目}$,$(p+q+1)\text{列目} \sim (p+q+r)\text{列目}$に制限した行列はいずれも上で置いた仮定により正定値対称行列である.また,$\delta_{0}^{2} = \frac{1}{4} \delta^{2 \prime} {\Delta^{2}}^{-1} \delta^{2}$である.以上より,$j=2$についても定理1におけるパラメータの条件を満たす.
上述の通り,式(1)の係数行列$K$は,対角成分が全て正である下三角行列とする.この仮定を維持しつつ,$K$が下記のブロック行列の形を取るという仮定を課す.
| $$K = \left( \begin{array}{ccc} \begin{matrix} K_{11} & \large{0} & \large{0} \\ K_{21} & K_{22} & \large{0} \\ K_{31} & \large{0} & K_{33} \end{matrix} \end{array} \right).$$ | (37) |
ここで,$K_{11} \in \mathbb{R}^{p \times p}$,$K_{22} \in \mathbb{R}^{q \times q}$,$K_{33} \in \mathbb{R}^{r \times r}$,$K_{21} \in \mathbb{R}^{q \times p}$,$K_{31} \in \mathbb{R}^{r \times p}$とし,$K_{11}$,$K_{22}$,$K_{33}$は対角成分が正の値を取る下三角行列とする.$K$の第1行第2列目および第1行第3列目のブロックは零行列と仮定したことにより,共通成分$X_{t,1}$の時刻$t$における微小時間での変化は,$X_{t,2}$や$X_{t,3}$には依存せず,$X_{t,1}$のみに依存する.さらに,$K$の第2行第3列目のブロックを零行列と仮定したことにより,$X_{t,2}$の時刻$t$における微小時間での変化は$X_{t,1}$と$X_{t,2}$に依存し,$X_{t,3}$には影響されないことが分かる.同様に,$K$の第3行第2列目のブロックを零行列と仮定したことにより,$X_{t,3}$の時刻$t$における微小時間での変化は$X_{t,1}$と$X_{t,3}$に依存し,$X_{t,2}$には依存しないことが分かる.
上述のパラメータの設定により,$X_{t,1}$が日米共通要因,$X_{t,2}$が米国固有要因,$X_{t,3}$が日本固有要因と「ほぼ」みなせる.ここで,「ほぼ」と記したのは,$X_{t}$の$\mathbb{P}$,$\mathbb{Q}^{1}$,$\mathbb{Q}^{2}$の下での確率過程を定める行列$K$,$K^1$,$K^2$の非対角ブロック成分(例えば式(37)の$K_{21}$)を零行列と仮定していないためである.
以上より,式(16)で与えられる債券のタームプレミアム$btp_{t}^{\tau,j}$と式(30)で与えられる株式のフォワードイールド$efy_{t}^{\tau,j}$は,次のような形式で表現される.
| $$\begin{split} btp_{t}^{\tau,j} &= F_{1}^{\tau j}(X_{t,1})+F_{2}^{\tau j}(X_{t,j+1}) + F_{3}^{\tau j}(X_{t,1},X_{t,j+1}) + C_{b}^{\tau,j}, \\ efp_{t}^{\tau,j} &= G_{1}^{\tau j}(X_{t,1})+G_{2}^{\tau j}(X_{t,j+1}) + G_{3}^{\tau j}(X_{t,1},X_{t,j+1}) + C_{e}^{\tau,j}+ Error_{t}^{\tau,j} . \end{split}$$ | (38) |
式(38)の第1式,第2式の右辺第1項が,債券のタームプレミアムと株式のフォワードイールドへの日米共通変数の寄与を表す項である.第2項は第$j$国の固有要因の寄与を表す項,第3項は共通要因と固有要因の交差からの寄与を表す項である.第4項は定数項,第2式第5項は式(30)における対数関数の線形近似に伴う誤差項$Error_{t}^{\tau,j}$を表す.
以下では,共通要因の次元を$p$,米国固有要因の次元を$q$,日本固有要因の次元を$r$とする設定を$(p,q,r)$モデルと呼ぶことにする.4節では,$(2,2,2)$モデル,$(1,3,3)$モデル,$(2,3,3)$モデルの推定を行う.
3.3 推定法本研究のモデルは,状態空間モデルとみなすことができる.状態変数$X_t$は3,2節で言及した通り,市場で直接観測されない潜在変数と仮定する.状態変数が潜在変数である状態空間モデルは,カルマンフィルタか非線形フィルタにより推定できることが知られている.カルマンフィルタは,状態の遷移を表す状態方程式と状態の関数として観測値を定める観測方程式が線形・ガウス型である場合に適用できる.それ以外の場合は,カルマンフィルタをそのまま適用することができず,非線形フィルタを適用することになる.
本研究では観測方程式が状態変数の非線形関数となるため,非線形フィルタの1種である拡張カルマンフィルタを適用する8.拡張カルマンフィルタは,ファイナンス分野の研究において潜在変数の推定にしばしば利用されている(例えば,Kim and Singleton (2012),Christensen and Rudebusch (2015)).
まず,本研究のモデルの状態方程式は式(1)に対応するものである.前小節での不変変換の仮定($\theta = 0_{\ell \times 1}$かつ$\Sigma$は単位行列$I$)を踏まえると,式(1)は,
| $$d (e^{Kt} X_{t}) = e^{Kt} dW_{t},$$ | (39) |
となる.したがって,状態方程式は,時間間隔を$\Delta t$とすると下記式となる.
| $$X_{t + \Delta t} = e^{-K \Delta t} X_{t} + \varepsilon_{t + \Delta t}.$$ | (40) |
ここで,$\varepsilon_{t + \Delta t} \sim N \left(0, \int_{0}^{\Delta t} e^{K(s - \Delta t)} e^{K'(s - \Delta t)}ds \right)$である.
時刻$t$での$j$国国債のゼロクーポンイールドの観測値を$by_{t}^{\tau,j,o}$,$j$国の株式指数の観測値を$S_{t}^{j,o}$,配当額の観測値を$D_{t}^{j,o}$,株式投資に伴う収益率の分散の観測値を$var_{t}^{j,o}$とする.このとき,観測方程式は以下の式(41)で与えられる.
| $$\begin{split} by_{t}^{\tau,j,o}&=by_{t}^{\tau, j}+ \tilde{\epsilon}_{t}^{j, \tau} = -\dfrac{1}{\tau} \left(X_{t}' A_{\tau}^{j} X_{t} + b_{\tau}^{j \prime} X_{t} + c_{\tau}^{j} \right) + \tilde{\epsilon}_{t}^{j, \tau}, \\ \log \dfrac{S_{t}^{j,o}}{S_{0}^{j,o}} &= \log \dfrac{S_{t}^{j}}{S_{0}^{j}}+\tilde{\epsilon}_{t}^{j, s}=X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t + \tilde{\epsilon}_{t}^{j, s}, \\ \dfrac{D_{t}^{j,o}}{S_{t}^{j,o}} &= \dfrac{D_{t}^{j}}{S_{t}^{j}}+\tilde{\epsilon}_{t}^{j, d}=X_{t}' \Delta^{j} X_{t} + \delta^{j \prime} X_{t} +\delta_{0}^{j} + \tilde{\epsilon}_{t}^{j, d}, \\ var_{t}^{j,o}&=Var\left( \dfrac{dS_{t}^{j} + D_{t}^{j} dt}{S_{t}^{j}} \right)+ \tilde{\epsilon}_{t}^{j, v}= (2E^{j} X_{t} + f^{j})' \Sigma \Sigma' (2E^{j} X_{t} + f^{j}) + \tilde{\epsilon}_{t}^{j, v}. \end{split}$$ | (41) |
式(41)の最左辺は観測値である.なお,$var_{t}^{j,o}$については,3.1節で記した通り,株式指数の月次変化率の過去12か月分の不偏分散を年率換算した値を用いる.具体的には,$\Delta=\frac{1}{12}$年,時刻$t$の$i$か月前の時刻$t-i\Delta$から$t-(i-1)\Delta$の期間に対応する月次対数収益率$\log\left(S_{t-(i-1)\Delta}^{j,o}/S_{t-i\Delta}^{j,o}\right)$を$r_{t-i+1}^{j,o}$と定義すると,$var_{t}^{j,o}$は次式で表される.
| $$var_{t}^{j,o} = \dfrac{12}{11} \sum_{i=1}^{12} \left(r_{t-12+i}^{j,o} - \dfrac{1}{12} \sum_{i=1}^{12} r_{t-12+i}^{j,o} \right)^{2}.$$ | (42) |
式(41)の1つ目の等号の右辺の式と最右辺の式の第1項はそれぞれ,モデルから得られる理論式を表しており,1つ目の式は式(12),2つ目の式は式(20),3つ目の式は式(21)で表されている,また,4つ目の$Var\left( \dfrac{dS_{t}^{j} + D_{t}^{j} dt}{S_{t}^{j}} \right)$は株式投資に係る収益率の理論分散を表しており,式(22)によって式(41)の4つ目の式の最右辺第1項で与えられる.式(41)の$\tilde{\epsilon}_{t}^{j, \ell}$($j=1,2, \ \ell = \tau, s, d, v$)は,観測誤差を表す確率変数であり,期待値$0$,分散$\sigma_{j, \ell}^2$の正規分布に従うと仮定する.また,互いに独立であると仮定する.
式(41)の観測方程式の左辺における時点$t$での観測ベクトルを$\boldsymbol{z}_{t}$と置くと,対数尤度は,
| $$-\dfrac{Tg}{2}\log(2\pi)-\dfrac{T}{2}\log|F_{t|t-1}| -\dfrac{1}{2} \displaystyle \sum_{t=1}^{T} (\boldsymbol{z}_{t} - \boldsymbol{z}_{t|t-1})' F_{t|t-1} (\boldsymbol{z}_{t} - \boldsymbol{z}_{t|t-1}),$$ |
と表される.ここで,$\boldsymbol{z}_{t|t-1}$は観測変数ベクトルの1期先予測,$F_{t|t-1}$は観測変数ベクトルの1期先分散共分散行列であり,両者とも拡張カルマンフィルタにより推定する.また,本研究の推定で用いるサンプルは2000年1月~2019年12月の240か月の月次データであることから$T=240$である.さらに,$g$は観測ベクトル$\boldsymbol{z}_{t}$の次元とし,$g=18$である.上記の対数尤度はモデルのパラメータの関数となっており,拡張カルマンフィルタで$\boldsymbol{z}_{t|t-1}$と$F_{t|t-1}$を推定しながら,対数尤度が最大となるパラメータを探索する.
本小節では,$(2,2,2)$モデル,$(1,3,3)$モデル,$(2,3,3)$モデルの推定結果を示す.
観測値への適合度を,株式指数以外の指標についてはRMSE(Root Mean Squared Error: 平均平方二乗誤差)によって,株式指数についてはRMSPE(Root Mean Squared Percentage Error: 平均平方二乗誤差率)によって評価する.3つのモデルの適合度の結果を,米国は表3に,日本は表4にまとめた.
| モデル | $0.5$ | $2$ | $5$ | $7$ | $10$ | $20$ | S&P500 | 配当利回り | 分散の平方根 |
|---|---|---|---|---|---|---|---|---|---|
| $(2,2,2)$ | $54.1$ | $30.0$ | $3.94$ | $5.06$ | $1.95$ | $24.0$ | $0.798$ | $29.6$ | $7.73$ |
| $(1,3,3)$ | $50.8$ | $30.1$ | $10.7$ | $9.65$ | $9.94$ | $30.5$ | $0.362$ | $0.532$ | $14.5$ |
| $(2,3,3)$ | $54.6$ | $30.2$ | $5.75$ | $3.47$ | $3.69$ | $28.4$ | $0.583$ | $0.437$ | $11.3$ |
| モデル | $0.5$ | $2$ | $5$ | $7$ | $10$ | $20$ | TOPIX | 配当利回り | 分散の平方根 |
|---|---|---|---|---|---|---|---|---|---|
| $(2,2,2)$ | $11.2$ | $0.407$ | $8.52$ | $7.55$ | $0.558$ | $17.2$ | $0.371$ | $53.1$ | $5.31$ |
| $(1,3,3)$ | $24.2$ | $14.7$ | $6.86$ | $2.53$ | $7.63$ | $24.1$ | $0.323$ | $50.8$ | $17.0$ |
| $(2,3,3)$ | $21.8$ | $11.8$ | $0.538$ | $2.79$ | $2.07$ | $16.5$ | $0.704$ | $48.6$ | $1.91$ |
いずれのモデルも$0.5$年金利の適合度が良くない.本研究では,短期ゾーン(0.5年,2年),中期ゾーン(5年,7年),長期・超長期ゾーン(10年,20年)の金利を満遍なく観測金利に配置している.これにより,短期金利の推定値が中長期ゾーンの金利からの影響を強く受けてしまい,その結果,適合度が悪化している可能性が考えられる.短期金利の適合度を向上させるためには,短期の年限の金利の観測値を長期の年限の金利の数に比べて増やして配置し,推定を行うことが考えられる.しかし,本研究は,投資期間が長期のリスクプレミアムを分析対象とするため,短期ゾーンに観測値を偏らせることなく分析を行っている.
| モデル | $(2,2,2)$ | $(1,3,3)$ | $(2,3,3)$ |
|---|---|---|---|
| 次元 | $6$ | $7$ | $8$ |
| 対数尤度 | $21369.1$ | $20976.3$ | $21463.2$ |
| BIC | $-41879.3$ | $-41023.4$ | $-41729.4$ |
表5は,3つのモデルの対数尤度とベイジアン情報量規準(Bayesian Information Criterion; BIC)を示している.$(2,2,2)$モデルのBIC値が最小であることから,以下では$(2,2,2)$モデルの結果に焦点を当てる.
表6は,$(2,2,2)$モデルのパラメータの推定値を示している.図1は,$(2,2,2)$モデルの状態変数$X_{t}$の拡張カルマンフィルタに基づく推定値を示している.第1変数と第2変数が日米共通変数であり,第3変数と第4変数が米国固有変数であり,第5変数と第6変数が日本固有変数である.第4変数の推定値の水準のスケールが他の5つの変数の推定値の水準のスケールと異なるため,図1では,第4変数とそれ以外の変数を分けて図示している.

| 行番号 | 列番号 | 推定値 | 行番号 | 列番号 | 推定値 | 行番号 | 列番号 | 推定値 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| $K_{11}^{1}$ | 1 | 1 | $0.0192$ | $K_{11}^{2}$ | 1 | 1 | $5.50 \times 10^{-8}$ | $K_{11}$ | 1 | 1 | $4.13$ |
| 2 | 1 | $-0.214$ | 2 | 1 | $0.0116$ | 2 | 1 | $-0.119$ | |||
| 2 | 2 | $2.44 \times 10^{-12}$ | 2 | 2 | $8.89 \times 10^{-8}$ | 2 | 2 | $0.183$ | |||
| $K_{21}^{1}$ | 1 | 1 | $0.155$ | $K_{31}^{2}$ | 1 | 1 | $-0.256$ | $K_{21}$ | 1 | 1 | $3.41 \times 10^{-5}$ |
| 1 | 2 | $-0.106$ | 1 | 2 | $-0.00309$ | 1 | 2 | $-5.67 \times 10^{-5}$ | |||
| 2 | 1 | $0.293$ | 2 | 1 | $-0.517$ | 2 | 1 | $1.85 \times 10^{-5}$ | |||
| 2 | 2 | $-0.109$ | 2 | 2 | $-0.00159$ | 2 | 2 | $6.13 \times 10^{-6}$ | |||
| $K_{22}^{1}$ | 1 | 1 | $0.0918$ | $K_{33}^{2}$ | 1 | 1 | $0.0281$ | $K_{22}$ | 1 | 1 | $9.10 \times 10^{-5}$ |
| 2 | 1 | $0.0425$ | 2 | 1 | $0.0816$ | 2 | 1 | $5.42 \times 10^{-6}$ | |||
| 2 | 2 | $0.00160$ | 2 | 2 | $0.0277$ | 2 | 2 | $3.00 \times 10^{-5}$ | |||
| $\theta^{1}$ | 1 | 1 | $2.29$ | $\theta^{2}$ | 1 | 1 | $0.492$ | $K_{31}$ | 1 | 1 | $1.76 \times 10^{-4}$ |
| 2 | 1 | $0.0198$ | 2 | 1 | $-3.37$ | 1 | 2 | $-5.11 \times 10^{-4}$ | |||
| 3 | 1 | $-3.63$ | 5 | 1 | $-2.01$ | 2 | 1 | $-9.87 \times 10^{-6}$ | |||
| 4 | 1 | $-3.01$ | 6 | 1 | $-3.13$ | 2 | 2 | $5.37 \times 10^{-5}$ | |||
| $\Psi^{1}$ | 1 | 1 | $9.85 \times 10^{-5}$ | $\Psi^{2}$ | 1 | 1 | $1.75 \times 10^{-5}$ | $K_{33}$ | 1 | 1 | $6.88 \times 10^{-4}$ |
| 2 | 1 | $-1.10 \times 10^{-5}$ | 2 | 1 | $3.34 \times 10^{-5}$ | 2 | 1 | $1.20 \times 10^{-4}$ | |||
| 2 | 2 | $6.84 \times 10^{-5}$ | 2 | 2 | $1.09 \times 10^{-4}$ | 2 | 2 | $1.84 \times 10^{-4}$ | |||
| 3 | 3 | $9.16 \times 10^{-4}$ | 5 | 5 | $2.76 \times 10^{-5}$ | $\delta^{1}$ | 1 | 1 | $-0.00173$ | ||
| 4 | 3 | $1.27 \times 10^{-4}$ | 6 | 5 | $1.07 \times 10^{-5}$ | 2 | 1 | $0.00148$ | |||
| 4 | 4 | $2.36 \times 10^{-5}$ | 6 | 6 | $1.47 \times 10^{-4}$ | 3 | 1 | $6.40 \times 10^{-4}$ | |||
| $\Delta^{1}$ | 1 | 1 | $9.85 \times 10^{-5}$ | $\Delta^{2}$ | 1 | 1 | $1.75 \times 10^{-5}$ | 4 | 1 | $1.95 \times 10^{-4}$ | |
| 2 | 1 | $-1.10 \times 10^{-5}$ | 2 | 1 | $3.34 \times 10^{-5}$ | $\delta^{2}$ | 1 | 1 | $4.91 \times 10^{-4}$ | ||
| 2 | 2 | $6.84 \times 10^{-5}$ | 2 | 2 | $1.09 \times 10^{-4}$ | 2 | 1 | $0.00171$ | |||
| 3 | 3 | $5.78 \times 10^{-4}$ | 5 | 5 | $2.70 \times 10^{-5}$ | 5 | 1 | $-6.83 \times 10^{-4}$ | |||
| 4 | 3 | $1.13 \times 10^{-4}$ | 6 | 5 | $1.03 \times 10^{-5}$ | 6 | 1 | $-1.67 \times 10^{-4}$ | |||
| 4 | 4 | $2.30\times 10^{-5}$ | 6 | 6 | $4.58 \times 10^{-5}$ | $\eta^{1}$ | 1 | 1 | $0.0338$ | ||
| $\varphi^{1}$ | 1 | 1 | $-2.49 \times 10^{-4}$ | $\varphi^{2}$ | 1 | 1 | $3.52 \times 10^{-4}$ | $\eta^{2}$ | 1 | 1 | $0.0133$ |
| 2 | 1 | $-0.00227$ | 2 | 1 | $0.00139$ | $\sigma_{1,S}$ | 1 | 1 | $0.0145$ | ||
| 3 | 1 | $0.0102$ | 5 | 1 | $-0.00218$ | $\sigma_{2,S}$ | 1 | 1 | $8.22 \times 10^{-5}$ | ||
| 4 | 1 | $6.54 \times 10^{-4}$ | 6 | 1 | $-0.00443$ | $\sigma_{1,d}$ | 1 | 1 | $0.00295$ | ||
| $\sigma_{1,0.5}$ | 1 | 1 | $0.00563$ | $\sigma_{2,0.5}$ | 1 | 1 | $0.00110$ | $\sigma_{2,d}$ | 1 | 1 | $0.00361$ |
| $\sigma_{1,2}$ | 1 | 1 | $0.00319$ | $\sigma_{2,2}$ | 1 | 1 | $2.69 \times 10^{-6}$ | $\sigma_{1,v}$ | 1 | 1 | $0.0243$ |
| $\sigma_{1,5}$ | 1 | 1 | $5.36 \times 10^{-4}$ | $\sigma_{2,5}$ | 1 | 1 | $8.41 \times 10^{-4}$ | $\sigma_{2,v}$ | 1 | 1 | $0.0192$ |
| $\sigma_{1,7}$ | 1 | 1 | $5.33 \times 10^{-4}$ | $\sigma_{2,7}$ | 1 | 1 | $7.51 \times 10^{-4}$ | ||||
| $\sigma_{1,10}$ | 1 | 1 | $2.37 \times 10^{-4}$ | $\sigma_{2,10}$ | 1 | 1 | $1.98 \times 10^{-8}$ | ||||
| $\sigma_{1,20}$ | 1 | 1 | $0.00237$ | $\sigma_{2,20}$ | 1 | 1 | $0.00168$ |
図2から図5は,$(2,2,2)$モデルに基づく米国の金利,株式,配当利回りの推定値と観測値の時系列方向のフィットを示したものである.5年,7年,10年金利,株式指数が高い精度を示していることが確認できるほか,20年金利も乖離が一時的に大きくなる場合はあるものの,サンプル期間を通じたフィットは概ね良好といえる.ただし,図2をみると,金利の短期ゾーン,特に0.5年金利は推定値と観測値の間に乖離がみられる.




図6から図9は,$(2,2,2)$モデルに基づく,日本の金利,株式,配当利回りの推定値と観測値の時系列方向のフィットを示したものである.$2$年金利,10年金利,株式指数は高い精度を示していることが確認できる.一方,$0.5$年金利や$20$年金利において,観測値と推定値の間に乖離が生じる時期があることが見て取れる.
また,図9の右図の通り,日本の配当利回りの推定値と観測値の間にずれがみられ,最大で$1\%$をやや上回る誤差が生じている時期がある.これは,株式指数と配当利回りの実際の値が,無裁定価格理論に照らし整合が取れない時期があることを示唆している.




図2~図9によって,株式指数の収益率の分散以外について,$(2,2,2)$モデルから得られる推定値の観測値に対するフィットを確認した.以上の$(2,2,2)$モデルの推定結果をまとめると,米国の短期ゾーンの金利,日本の$0.5$年金利,$20$年金利,配当利回りの適合度が悪化する時期がみられるものの,総じて良好なフィットを示すパラメータ推定値を得ることができたと考えられる.

図10は,S&P500およびTOPIXの収益率について,式(42)で定義したヒストリカル分散$var_{t}^{1,o}$, $var_{t}^{2,o}$の平方根(以下,ヒストリカルボラティリティ)と,$(2,2,2)$モデルから推定されたインプライドボラティリティを比較したプロットである.S&P500,TOPIXの双方とも,モデルのインプライドボラティリティは,観測値であるヒストリカルボラティリティと水準に差異が生じている時期がある.
この点を評価するため,$(2,2,2)$モデルの枠組みを仮定しつつ,状態空間モデルの観測方程式(式(41))から株式指数の収益率の分散に係る式(式(41)の4つ目の式)を取り除いた形で推定を行い,今までみてきた$(2,2,2)$モデルの推定結果との比較を行うことにする.この$(2,2,2)$モデルの枠組みで式(41)の観測方程式の第4式を取り除いた観測方程式を持つ形の設定を「分散無し$(2,2,2)$モデル」と呼ぶことにする.なお,「分散無し$(2,2,2)$モデル」は,観測方程式に株式指数の収益率の分散を含まない点が「$(2,2,2)モデル$」と異なるだけで,得られるパラメータと状態変数の推定値からインプライド分散の理論値を計算することができる点には注意が必要である.また,以下では,「分散無し$(2,2,2)$モデル」との混同を避けるため,$(2,2,2)$モデルを「通常の$(2,2,2)$モデル」と呼ぶ場合がある.
| 米国 | $0.5$ | $2$ | $5$ | $7$ | $10$ | $20$ | S&P500 | 配当利回り | 分散の平方根 |
|---|---|---|---|---|---|---|---|---|---|
| $(2,2,2)$ | $54.1$ | $30.0$ | $3.94$ | $5.06$ | $1.95$ | $24.0$ | $0.798$ | $29.6$ | $7.73$ |
| 分散無し$(2,2,2)$ | $50.9$ | $27.7$ | $3.00$ | $4.20$ | $3.92$ | $19.6$ | $0.931$ | $26.7$ | -- |
| 日本 | $0.5$ | $2$ | $5$ | $7$ | $10$ | $20$ | TOPIX | 配当利回り | 分散の平方根 |
|---|---|---|---|---|---|---|---|---|---|
| $(2,2,2)$ | $11.2$ | $0.407$ | $8.52$ | $7.55$ | $0.558$ | $17.2$ | $0.371$ | $53.1$ | $5.31$ |
| 分散無し$(2,2,2)$ | $24.5$ | $15.5$ | $0.644$ | $3.31$ | $0.767$ | $11.8$ | $0.800$ | $54.4$ | -- |
表7は,2つのモデルの適合度を比較した結果を示している.通常の$(2,2,2)$モデルの結果は,表3,表4に記載した内容と同じである.分散無し$(2,2,2)$モデルの結果は,通常の$(2,2,2)$モデルの結果に比べ,米国の短中期ゾーンの金利や日米20年金利の適合度に改善がみられる.米国の株式指数,配当利回り,日本の短期ゾーンの金利の適合度は通常の$(2,2,2)$モデルと比べて悪い結果を示しているのものもあるが,通常の$(2,2,2)$モデルと遜色ない市場適合度を示しているといえる.

図11は,分散無し$(2,2,2)$モデルおよび通常の$(2,2,2)$モデルのパラメータと状態変数の推定値から得られるそれぞれの株式指数の収益率のインプライドボラティリティと,ヒストリカルボラティリティを図示したものである.日米の株式指数の両方において,分散無し$(2,2,2)$モデルによるインプライドボラティリティと他の2つのボラティリティ(通常の$(2,2,2)$モデルとヒストリカルボラティリティ)との水準には,多くの時期で差異が見られる.

株式指数のインプライドボラティリティの時系列データには,本研究の分析対象期間である2000年初から2019年末の全期間をカバーするものは存在しない.しかし,脚注6で触れたように,米国の株式指数については「CBOE S&P500 3-Month Volatility Index」が2007年12月から,日本の株式指数については「日経ボラティリティインデックス」が2014年1月から利用できる.これらのインプライドボラティリティの市場データと,通常の$(2,2,2)$モデルおよび分散無し$(2,2,2)$モデルの推定値から得られるインプライドボラティリティを比較したものが図12である.
図12をみると,分散無し$(2,2,2)$モデルのインプライドボラティリティよりも,通常の$(2,2,2)$モデルのインプライドボラティリティの方が市場で観測されるインプライドボラティリティとの差が小さいことが分かる.分散無し$(2,2,2)$モデルは,ゼロクーポンイールド,株式,配当利回りへの適合度では通常の$(2,2,2)$モデルとほぼ同等の精度を示していたが,株式指数の収益率のボラティリティに関しては,市場データが入手可能な期間において,通常の$(2,2,2)$モデルよりも精度が劣ることが確認された.
したがって,次節以降では,通常の$(2,2,2)$モデルに基づき,債券と株式のリスクプレミアムの計測を行うことにする.なお,$(2,2,2)$モデルのゼロクーポンイールド,株式,配当利回りへの適合度を維持しつつ,株式指数の収益率の分散(ボラティリティ)への適合度を高めるには,状態変数の次元を増やしたモデルが必要と考えられる.そのようなモデルの模索は今後の課題とする.
4.2 債券のリスクプレミアムの計測4.1節で得られたモデルのパラメータおよび状態変数の推定値をもとに,日米の債券のリスクプレミアムを計測する.本研究では,式(16)で定義したタームプレミアムの形で債券のリスクプレミアムを計測する.
まず,米国債のタームプレミアムの計測結果を示す.図13の左の図は,米国債の各年限のタームプレミアムの計測結果を示している.右の図は10年タームプレミアムと2年タームプレミアムの差(長短スプレッド)を図示している.
Adrian et al. (2013a),Chung et al. (2017),Berardi (2023)は,債券のタームプレミアムは反景気循環的(countercyclical)に推移する,すなわち,タームプレミアムは景気後退期に上昇し,景気拡張期に低下すると指摘している.NBER(全米経済研究所)の米国の景気判断によると,推定のサンプル期間中の2001年3月~2001年11月と2007年12月~2009年6月が景気後退期に当たり,2000年1月~2001年3月,2001年11月~2007年12月,2009年6月~2019年12月が景気拡張期に当たる9.
図13をみると,特に10年タームプレミアムが景気拡張期に低下傾向を示し,景気後退期に上昇傾向を示しているようにみえる.また,10年と2年のタームプレミアムの長短スプレッドは反景気循環的であるようにみえる.

これらの点を明確にするため,2001年3月~2001年11月,2001年11月~2007年12月,2007年12月~2009年6月,2009年6月~2019年12月に,2年と10年のタームプレミアム,それらの長短スプレッドがどの程度変化したのかを表8にまとめた.
表8をみると,10年のタームプレミアムと10年と2年の長短スプレッドは,景気拡張期に低下し,景気後退期に上昇しており,反景気循環的な動きを示していることが分かる.
| 2001年3月~2001年11月 景気後退期 |
2001年11月~2007年12月 景気拡張期 |
2007年12月~2009年6月 景気後退期 |
2009年6月~2019年12月 景気拡張期 |
|
|---|---|---|---|---|
| 2年 | $0.122$ | $0.034$ | $0.063$ | $-0.383$ |
| 10年 | $0.736$ | $-0.119$ | $0.858$ | $-2.128$ |
| 10年2年 スプレッド |
$0.614$ | $-0.153$ | $0.794$ | $-1.745$ |
図14は,米国債のタームプレミアムへの日米共通要因,米国固有要因,交差要因の寄与度を示したものである.図14の左図は2年タームプレミアムへの寄与度,右図は10年タームプレミアムへの寄与度を示している.

2年タームプレミアム,10年タームプレミアムの双方とも,その変動は,日米共通要因の寄与から主に生じていることが見て取れる.なお,米国固有要因は主要因ではないが,2年タームプレミアムをみると,2008年末~2013年末に固有要因が負の値を示している.米国金融政策の量的緩和政策第1弾~第3弾(QE1,QE2,QE3)の時期と重なっており,これらの政策が2年のタームプレミアムの押し下げ要因として寄与した可能性が考えられる.
10年タームプレミアムを定める各種要因が景気拡張期・後退期にどのような変化を示したのかを表9にまとめた.表からは,どの期間においても日米共通要因が反景気循環的にタームプレミアムの変動を主導していることが分かる.
| 2001年3月~2001年11月 景気後退期 |
2001年11月~2007年12月 景気拡張期 |
2007年12月~2009年6月 景気後退期 |
2009年6月~2019年12月 景気拡張期 |
|
|---|---|---|---|---|
| 共通要因 | $0.763$ | $-0.193$ | $1.258$ | $-2.701$ |
| 固有要因 | $-0.007$ | $0.145$ | $-0.139$ | $0.438$ |
| 交差要因 | $-0.019$ | $0.029$ | $-0.262$ | $0.135$ |
次に,日本国債のタームプレミアムの計測結果を示していく.図15は,日本国債の各年限のタームプレミアムの計測結果を示している.

日本国債のタームプレミアムが反景気循環的かどうかを以下で確認する.内閣府が定める景気基準日付によれば,本研究の推定のサンプル期間中,2000年1月~2000年11月,2002年1月~2008年2月,2009年3月~2012年3月,2012年11月~2018年10月が景気拡張期に当たり,2000年11月~2002年1月,2008年2月~2009年3月,2012年3月~2012年11月,2018年10月~2019年12月が景気後退期に相当する10.
| 2000年1月~2000年11月 景気拡張期 |
2002年1月~2008年2月 景気拡張期 |
2009年3月~2012年3月 景気拡張期 |
2012年11月~2018年10月 景気拡張期 |
|
|---|---|---|---|---|
| 2年 | $-0.042$ | $-0.183$ | $-0.081$ | $-0.190$ |
| 10年 | $-0.232$ | $-0.865$ | $-0.250$ | $-0.749$ |
| 10年2年 スプレッド |
$-0.189$ | $-0.682$ | $-0.168$ | $-0.560$ |
| 2000年11月~2002年1月 景気後退期 |
2008年2月~2009年3月 景気後退期 |
2012年3月~2012年11月 景気後退期 |
2018年10月~2019年12月 景気後退期 |
|
|---|---|---|---|---|
| 2年 | $0.135$ | $0.090$ | $-0.063$ | $-0.040$ |
| 10年 | $0.657$ | $0.333$ | $-0.329$ | $-0.199$ |
| 10年2年 スプレッド |
$0.522$ | $0.243$ | $-0.267$ | $-0.158$ |
表10は,日本の景気拡張期・後退期の2年と10年タームプレミアムのそれぞれの変化とタームプレミアムの長短スプレッドの変化を示したものである.景気拡張期においては,いずれも負の値を示しており,タームプレミアムやその長短スプレッドが低下したことを示している.日本の景気後退期のタームプレミアムと長短スプレッドの変化については,2000年11月~2002年1月と2008年2月~2009年3月には上昇を示し反景気循環的な動きとなる一方,2012年3月~2012年11月と2018年10月~2019年12月はタームプレミアムや長短スプレッドが低下していることが分かる.
図16は,日本国債のタームプレミアムへの日米共通要因,日本固有要因,交差要因の寄与度を示したものである.図16の左図は2年タームプレミアムへの寄与度,右図は10年タームプレミアムへの寄与度を示している.米国債のタームプレミアムと同様,共通要因の変動の方が固有要因の変動より大きいことが分かる.

| 2000年1月~2000年11月 景気後退期 |
2002年1月~2008年2月 景気後退期 |
2009年3月~2012年3月 景気後退期 |
2012年11月~2018年10月 景気後退期 |
|
|---|---|---|---|---|
| 共通要因 | $-0.381$ | $0.374$ | $0.117$ | $-0.193$ |
| 固有要因 | $0.140$ | $-1.149$ | $-0.268$ | $-0.550$ |
| 交差要因 | $0.009$ | $-0.089$ | $-0.098$ | $-0.006$ |
| 2000年11月~2002年1月 景気後退期 |
2008年2月~2009年3月 景気後退期 |
2012年3月~2012年11月 景気後退期 |
2018年10月~2019年12月 景気後退期 |
|
|---|---|---|---|---|
| 共通要因 | $0.488$ | $-0.059$ | $-0.468$ | $-0.684$ |
| 固有要因 | $0.174$ | $0.329$ | $-0.005$ | $-0.027$ |
| 交差要因 | $-0.005$ | $0.063$ | $0.144$ | $0.513$ |
表11に,10年タームプレミアムを定める各種要因が景気拡張期・後退期にどのような変化を示したのかをまとめた.同表をみると,景気拡張期の寄与は2000年1月~2000年11月を除けば共通要因に比べて固有要因の低下の寄与が大きいことが見て取れる.景気後退期は,2000年11月~2002年1月は共通要因の上昇寄与が固有要因より大きく,2008年2月~2009年3月は固有要因の上昇の寄与が大きかった.また,2012年3月~2012年11月,2018年10月~2019年12月の景気後退期は,共通要因の低下がタームプレミアムの変動を主導したことが分かる.
4.3 株式のリスクプレミアムの計測本小節では,日米株式のゼロクーポンイールドとリスクプレミアムの代替指標である株式のフォワードイールドの計測結果を示す.
4.3.1 株式のゼロクーポンイールドまず,米国株式指数(S&P500)のゼロクーポンイールドの計測結果を示していく.図17の左の図は,S&P500における年限別のゼロクーポンイールドの推移を図示したものである.サンプル期間の多くの期間で,短期の年限のゼロクーポンイールドが長期の年限のイールドの水準を上回って推移していることが分かる.一方で,10年の年限を除く全てのイールドが同程度の水準を取る時期が存在することも分かる.さらに,サンプル期間の後半で,5年や7年のイールドが0.5年のイールドを上回って推移していることも見て取れる.
図17の右の図は,株式ゼロクーポンイールドの年限毎の期間平均値を期間構造の形で図示したものである.サンプル期間全体の平均イールドカーブは,短期が長期のイールドを上回る逆イールドの形状となっている.なお,株式のゼロクーポンイールドカーブが逆イールドの形状を取ることが多い点は,Binsbergen et al. (2013),Binsbergen and Koijen (2017)などで指摘されている.

図17の右の図は,サンプル期間全体の期間平均値だけではなく,2015年1月以降の期間平均値の期間構造も示している.同期間の期間構造は,年限が5年(60か月)程度までは右上がりとなり,それ以上に年限が伸びると右下がりの形状となっている.
続いて,日本株(TOPIX)のゼロクーポンイールドの計測結果を示す.図18の左の図は,日本の株式指数の年限別ゼロクーポンイールドの推移を図示したものである.サンプル期間中,短期の年限のゼロクーポンイールドは,長期の年限のイールドに比べて高い水準で推移している.米国の株式ゼロクーポンイールドでは,長期の年限のイールドが短期の年限のイールドと同水準を取る,もしくは上回る時期がみられたが,日本ではそのような年限間のイールドの水準の逆転は生じていない.
図18の右の図は,株式ゼロクーポンイールドの年限毎の期間平均値を期間構造の形で図示したものである.サンプル期間全体の平均のイールドカーブは,短期が長期のイールドを上回る逆イールドの形状となっている.

株式のフォワードイールドは,株式と債券のゼロクーポンイールドの差として定義されるものである(式(30)参照).この4.3.2節では,日米の株式のフォワードイールドの計測結果を示す.
はじめに米国の結果を示す.図19は,S&P500の年限別フォワードイールドの計測値の推移を示したものである.株式の年限別ゼロクーポンイールドの推移と同様,サンプル期間の多くで,短期の年限のフォワードイールドが長期の年限のイールドを上回る水準で推移している.ただし,図19は,7年フォワードイールドが短期の年限のフォワードイールドと同程度か,上回って推移している時期が存在していることも示している.

Breugem et al. (2023)は,経済成長のボラティリティ指標(Expected Growth Volatility; EGV)が上昇する時,すなわち,経済環境の不確実性が高まる時に株式のフォワードイールドが上昇することを示している.図19の0.5年,2年,5年の年限のイールドをみると,2000年代初め,2008年の世界金融危機が発生した時期,2011年後半の欧州債務危機が深刻化した時期などに水準を大きく上昇させている.このことは,Breugem et al. (2023)の結果と整合性がとれている.
図20は,特定の日における株式フォワードイールドの期間構造を示したものである.同図の2008年12月と2013年12月のイールドカーブは,逆イールドの形状を示している.逆イールドは,他の多くの日にみられる典型的な形状である.一方,図中の2006年12月,2016年12月,2018年12月のイールドカーブでは,短期の年限から年限5・6年にかけて緩やかにフォワードイールドの水準が高くなり,より長期の年限になると水準が低下していく形状となっている.

図21は,フォワードイールドの長短スプレッド(7年と2年のスプレッドと5年と6か月のスプレッド)の推移を示したものである.

フォワードイールドの長短スプレッドと景気循環との関係は,Binsbergen et al. (2013)やBreugem et al. (2023)で調べられており,いずれの研究でも株式のフォワードイールドの長短スプレッドは順景気循環的(procyclical)であるとしている.図21をNBERの景気後退期・拡張期と照らし合わせてみると,フォワードイールドの長短スプレッドが順景気循環的であることが分かる.表12に,景気拡張期と後退期における長短スプレッドの変化幅をまとめた.以上の結果は,米国株のフォワードイールドの長短スプレッドが順景気循環的であることを示しており,先行研究の結果と整合的である.
| 2001年3月~2001年11月 景気後退期 |
2001年11月~2007年12月 景気拡張期 |
2007年12月~2009年6月 景気後退期 |
2009年6月~2019年12月 景気拡張期 |
|
|---|---|---|---|---|
| 5年6か月 スプレッド |
$-2.072$ | $2.164$ | $-5.215$ | $8.174$ |
| 7年2年 スプレッド |
$-0.533$ | $2.094$ | $-4.167$ | $4.339$ |
図22は,米国株式のフォワードイールドに対する日米共通要因,米国固有要因,交差要因の寄与度の推移を図示したものである.左の図は,2年フォワードイールド,右の図は7年フォワードイールドへの各種要因の寄与度を示している.なお,図中の「近似誤差」は式(30)における$error$項を表しており,対数関数を線形近似した際に生じた誤差の値である.

図22の左の図の2年イールドの要因分解をみると,固有要因の変動が同イールドの変動の主要因であることが分かる.一方,図22の右の図の7年のイールドの変動要因をみると,共通要因の変動の寄与が大きいことが分かる.
7年イールドと2年イールドの長短スプレッドの変動要因毎の寄与度の推移を図23に図示した.
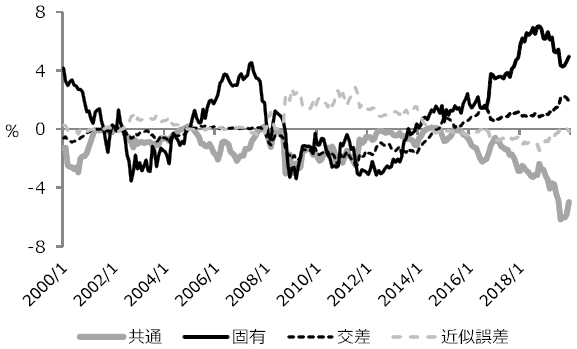
フォワードイールドの長短スプレッドの各種要因と景気循環との関係を明らかにするため,各種要因が景気拡張期・後退期でどのように変化しているのかを表13にまとめた.
| 2001年3月~2001年11月 景気後退期 |
2001年11月~2007年12月 景気拡張期 |
2007年12月~2009年6月 景気後退期 |
2009年6月~2019年12月 景気拡張期 |
|
|---|---|---|---|---|
| 共通要因 | $0.144$ | $0.362$ | $-1.765$ | $-3.394$ |
| 固有要因 | $-0.710$ | $2.141$ | $-2.966$ | $6.126$ |
| 交差要因 | $-0.054$ | $-0.0182$ | $-1.260$ | $3.262$ |
| 近似誤差 | $0.086$ | $-0.390$ | $1.824$ | $-1.654$ |
表13をみると,固有要因の寄与度の絶対値がどの局面においても大きく,さらに当該要因が順景気循環的であることが分かる.
次に,日本株のフォワードイールドの計測結果を示していく.図24の左の図は,日本の年限別株式フォワードイールドの計測値の推移を示している.年限の短いフォワードイールドほど高水準であることが分かる.年限間の水準の逆転はみられない.

図24の右の図は,株式フォワードイールドの年限別期間平均の期間構造を示したものである.短期の年限から約15年の年限にかけ,年限の伸びとともにイールドの水準が低下していく逆イールドの形状を示している.

図25は,日本株のフォワードイールドの5年と6か月の長短スプレッドと7年と2年の長短スプレッドの推移を図示したものである.米国株式のフォワードイールドの長短スプレッドが順景気循環的であることは上で確認した通りだが,日本について成立しているのかどうかを以下で確認する.
表14は,日本の景気拡張・後退期におけるフォワードイールドの長短スプレッドの変化幅を示したものである.景気拡張期では,2009年3月~2012年3月以外は,長短スプレッドは上昇し,順景気循環的な変動を示していることが分かる.景気後退期では,長短スプレッドが上昇する時期も存在していたことが分かる.
| 2000年1月~2000年11月 景気拡張期 |
2002年1月~2008年2月 景気拡張期 |
2009年3月~2012年3月 景気拡張期 |
2012年11月~2018年10月 景気拡張期 |
|
|---|---|---|---|---|
| 5年6か月 スプレッド |
$0.716$ | $2.550$ | $-0.783$ | $0.788$ |
| 7年2年 スプレッド |
$0.573$ | $2.960$ | $-0.208$ | $0.992$ |
| 2000年11月~2002年1月 景気後退期 |
2008年2月~2009年3月 景気後退期 |
2012年3月~2012年11月 景気後退期 |
2018年10月~2019年12月 景気後退期 |
|
|---|---|---|---|---|
| 5年6か月 スプレッド |
$-1.078$ | $-0.214$ | $0.445$ | $0.089$ |
| 7年2年 スプレッド |
$-1.205$ | $-0.251$ | $0.524$ | $0.267$ |
図26は,日本株式のフォワードイールドへの日米共通要因,日本固有要因,交差要因の寄与の推移を図示したものである.左の図は,2年フォワードイールド,右の図は7年フォワードイールドへの各種要因の寄与度を示している.

図27は,7年イールドと2年イールドの長短スプレッドへの各種要因の寄与度の推移を図示したものである.

日本株のフォワードイールドの長短スプレッドの各種要因と景気との関係を明らかにするため,各種要因が景気拡張期・後退期でどのように変化しているのかを表15にまとめた.
| 2000年1月~2000年11月 景気拡張期 |
2002年1月~2008年2月 景気拡張期 |
2009年3月~2012年3月 景気拡張期 |
2012年11月~2018年10月 景気拡張期 |
|
|---|---|---|---|---|
| 共通要因 | $0.370$ | $-0.255$ | $-0.723$ | $-0.646$ |
| 固有要因 | $-0.141$ | $2.850$ | $0.523$ | $2.015$ |
| 交差要因 | $0.305$ | $0.043$ | $-0.065$ | $-0.093$ |
| 近似誤差 | $0.039$ | $0.322$ | $0.058$ | $-0.284$ |
| 2000年11月~2002年1月 景気後退期 |
2008年2月~2009年3月 景気後退期 |
2012年3月~2012年11月 景気後退期 |
2018年10月~2019年12月 景気後退期 |
|
|---|---|---|---|---|
| 共通要因 | $0.201$ | $0.617$ | $0.480$ | $0.323$ |
| 固有要因 | $-1.493$ | $-0.969$ | $0.084$ | $0.321$ |
| 交差要因 | $-0.266$ | $-0.082$ | $0.143$ | $-0.017$ |
| 近似誤差 | $0.354$ | $0.183$ | $-0.183$ | $-0.360$ |
表15からは,景気拡張期と景気後退期の多くで,フォワードイールドの長短スプレッドに対して,日本固有要因が景気循環と同じ方向に作用していることが分かる.一方,共通要因は景気循環と逆の方向に作用していることが分かる.共通要因の寄与と固有要因の寄与を絶対値で比較してみると,2002年1月~2008年2月,2012年11月~2018年10月の景気拡張期と2000年11月~2002年1月,2008年2月~2009年3月の景気後退期に固有要因の寄与が共通要因を上回り,それ以外の期間は共通要因が上回ることが分かった.
本研究では,2次ガウシアンモデルに基づき,多通貨建ての債券と株式の無裁定同時価格付けモデルを構築し,モデルの応用として債券と株式のリスクプレミアムの期間構造に関する実証分析を行った.
株式のリスクプレミアムの期間構造に関する多くの先行研究で,代表的個人の効用最大化に基づく均衡アプローチが採用されている.一方,本研究は,誘導型モデルに基づくアプローチを採用し,市場価格への適合性の高さを維持しながら,世界金融危機以降の先進国の超低金利イールドカーブや株価・金利のボラティリティの確率変動を表現可能な柔軟なモデルを構築し,そのようなモデルを用いてリスクプレミアムの期間構造を計測し,その性質を調べた.
本研究の理論面での新しさは,2次ガウシアンモデルの枠組みで配当ストリップスの価格表現を導出した点にある.従来の誘導型モデルに基づく研究では,アフィンガウシアンモデルによる配当ストリップスの解析表現を得るまでにとどまっていたが,本研究の結果は,金融市場のより現実的な状況を反映した形で株式のリスクプレミアムの期間構造を分析することを可能にするものである.
また,本研究では,日米の金融市場の時系列データを用いてモデルの推定を行い,観測値に高い適合性を示すパラメータと状態変数を得た.これらの推定値をもとに,日米の債券のタームプレミアムや株式のフォワードイールドを計測し,(i)債券のタームプレミアムが反景気循環的であること,(ii)株式のフォワードイールドの長短スプレッドが順景気循環的であること,という先行研究で指摘されてきたリスクプレミアムに関する性質が,日米の多くの期間で成り立っていることを本研究で得たパラメータの下で確認することができた.
本研究では,金利,株式指数,債券および株式のリスクプレミアムの解析表現を状態変数の非線形関数として得たが,非線形モデルの推定結果は線形モデルと異なり解釈が難しい場合がある.この点を改善するため,金利や株価を決定する複数の状態変数を「国内外共通要因」と「各国固有要因」に分けるようなパラメータと状態変数の設定を組み込み,その下で推定を行った.これにより,債券のタームプレミアムや株式のフォワードイールドに対して,国内外要因や国固有要因の寄与度を定量的に把握することができるようになった.本研究の実証分析では,(i)米国債券のタームプレミアムの変動は日米共通要因が主導していること,(ii)日本国債のタームプレミアムは景気拡張期に固有要因の低下方向への寄与が大きいこと,(iii)米国株式のフォワードイールドの長短スプレッドには,固有要因の順景気循環的な変動が大きく寄与していること,(iv)日本株のフォワードイールドの長短スプレッドは固有要因が順景気循環的な寄与を示す一方で,共通要因は反景気循環的な寄与を示すこと,などが明らかになった.
本研究には幾つか課題が残されている.まず,本研究では,2019年末までのデータを用いて実証分析を行ったが,2020年初から最近にかけての約5年間で,日米の経済・金融動向には,両国のインフレ率の上昇や,それに伴う中央銀行の金融政策変更など,顕著な変化がみられている.本研究では,理論構築および実証分析において実体経済の変数を考慮していないが,これらの変数をモデルに組み込むことができれば,債券や株式のリスクプレミアムの期間構造に対する,近年の日米両国の経済・金融動向の変化からの影響を明らかにすることができると考えられる.また,他の課題として,パラメータの推定値の妥当性の確認方法が限定的である点が挙げられる.本研究では「観測値へのフィットを得ることができているか」と「先行研究で示されているリスクプレミアムの典型的な性質を計測値が捉えているか」という点に絞って推定値の妥当性を確認した.実証分析に用いるモデルの統計学的観点からの妥当性確認を行い,より適切なモデルを模索することは今後の課題としたい.
本研究を進めるにあたり,牧本直樹先生(筑波大学),鈴木雅貴先生(一橋大学),一橋大学金融研究会参加者の皆様から貴重なコメントを頂いた.また,論文の査読者からは内容の改善に資する有益なコメントを多数頂戴した.ここに記して感謝の意を表する.ただし,本稿のありうべき誤りは筆者本人に帰するものである.なお,本研究の一部は,JSPS科研費(20K01768)の助成を受けた.
1 Cox et al. (1985)は,ショートレートの確率変動が1ファクターの平方根過程に従うとするCIRモデルを提案した.
2 Binsbergenらの研究をサーベイした日本語の文献に田代(2023)がある.
3 Giglio et al. (2024)は,線形ファクターモデルに基づき分析を行っている.
4 Filipovi´c and Willems (2020)は,多項式過程に従う状態変数を用いて金利や配当をモデル化し,配当を原資産とする金融派生商品の価格公式を導出している.下限金利を持ち,配当の正値性を保証するモデルである.一方,リスク中立測度の下でのモデリングとキャリブレーションにとどまり,リスクプレミアムの分析は行っていない.
5 株式のリスクプレミアムを定義する際,Binsbergen et al. (2013) やBansal et al. (2021)を初めとする幾つかの研究では,株式ゼロクーポンイールドと実質債のゼロクーポンイールドの差に配当の成長率の期待値を加算した値を用いている. 一方,本研究の定義は名目債の利回りを用いたものである.したがって,厳密には,本研究と先行研究における定義は異なっている.
6 S&P500を原資産とするオプション価格から計算されたインプライドボラティリティの2007年12月以降の時系列データが,セントルイス連銀の「FRED」(https://fred.stlouisfed.org/series/VXVCLS)から取得できる.日本については,日経平均を原資産とするインプライドボラティリティ指数である「日経ボラティリティインデックス」の直近10年間の時系列データが利用可能である(https://indexes.nikkei.co.jp/nkave/index/profile?idx=nk225vi).
7 アフィン型金利期間構造モデルの不変変換について,日本語の文献では今井(2003)が詳しい.
8 拡張カルマンフィルタを含めた非線形フィルタの概要については,片山(2017)を参照されたい.
9 2001年3月を景気の山とする景気拡張は1991年3月に始まった.また,2009年6月を景気の谷とする景気拡張は2020年2月まで続いた.
10 2000年11月を景気の山とする景気拡張期は1999年1月より始まった.また,2018年10月を景気の山とする景気後退は2020年5月まで続いた.
式(7)を用いて,式(8)にファインマン=カックの定理を適用すると,
| $$\dfrac{\partial P_{t}^{\tau, j}}{\partial t} +\dfrac{\partial P_{t}^{\tau, j}}{\partial X_{t}} K^{j} (\theta^{j} -X_{t}) + \dfrac{1}{2} \mathrm{Tr} \left(\dfrac{\partial^2 P_{t}^{\tau, j}}{\partial X_{t} \partial X_{t}'} \Sigma \Sigma' \right) = r_{t}^{j} = X_{t}' \Psi^{j} X_{t} + {\varphi^{j \prime}} X_{t} + \eta^{j},$$ |
を得る.
$P_{t}^{\tau, j}$の解表現として$P_{t}^{\tau, j}=\exp \left(X_{t}' A_{\tau}^{j} X_{t} + b_{\tau}^{j \prime} X_{t} + c_{\tau}^{j} \right)$と予想し,これを上の式に代入する.その結果,$X_{t}$に関する恒等式が得られ,$X_{t}$の次数に応じた係数比較を行うと式(10)を得る.
付録B Kikuchi (2016)による株価の解析式の導出本付録の内容は,Kikuchi (2016)により提案された株価の解析式の導出の概要を示すものである.
時刻$t$で瞬間的な配当額$D_{t}^{j}=(X_{t}' \Delta^{j} X_{t} + \delta^{j \prime} X_{t} +\delta_{0}^{j})\exp \left( X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t \right)$の支払いがある証券があり,時刻$T$まで連続的に支払いが行われるとする.さらに,この証券は,時刻$T$で$\overline{D}_{T}^{j}=\exp \left( X_{T}' E^{j} X_{T} + f^{j \prime} X_{T} + g^{j} T \right)$の支払いを行うとする.この証券の時刻$t$での価格を$S_{t}^{T,j}$とすると,次式が成り立つ.
| $$S_{t}^{T,j} = E_{t}^{\mathbb{Q}^{j}} \left[\displaystyle \int_{t}^{T} \exp\left(- \displaystyle \int_{t}^{s} r_{u}^{j} du \right) D_{s}^{j}ds +\exp\left(- \displaystyle \int_{t}^{T} r_{u}^{j} du \right) \overline{D}_{T}^{j}\right].$$ | (43) |
式(7)を用いて,式(43)にファインマン=カックの定理を適用すると,
| $$\dfrac{\partial S_{t}^{T,j}}{\partial t} +\dfrac{\partial S_{t}^{T, j}}{\partial X_{t}} K^{j} (\theta^{j} -X_{t}) + \dfrac{1}{2} \mathrm{Tr} \left(\dfrac{\partial^2 S_{t}^{T, j}}{\partial X_{t} \partial X_{t}'} \Sigma \Sigma' \right) = r_{t}^{j} = X_{t}' \Psi^{j} X_{t} + {\varphi^{j \prime}} X_{t} + \eta^{j},$$ |
を得る.
$S_{t}^{T, j}$の解表現として$S_{t}^{T, j}=\exp \left(X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t \right)$と予想し,これを上の偏微分方程式に代入すると$X_{t}$に関する恒等式が得られ,$X_{t}$の次数に応じた係数比較を行うと式(19)を得る.
上記証券の満期$T$に関して$T \rightarrow \infty$とする時,次の「横断性条件」に関する補題が成り立つ.
補題1. 式(21)の通り,
| $$\dfrac{D_{t}^{j}}{S_{t}^{T, j}} = X_{t}' \Delta^{j} X_{t} + \delta^{j \prime} X_{t} +\delta_{0}^{j}$$ |
が常に非負のとき,
| $$\displaystyle \lim_{T \rightarrow \infty} E_{t}^{\mathbb{Q}^{j}} \left[ \exp \left( -\int_{t}^{T} r_{u}^{j} du \right) \overline{D}_{T}^{j} \right] = 0.$$ |
証明はMamaysky (2002)やKikuchi (2016)を参照のこと.
定理1の証明
$\Delta^{j}$が正定値行列かつ$\delta_{0}^{j} = \frac{1}{4} \delta^{j \prime} {\Delta^{j}}^{-1} \delta^{j}$なので, 補題1の条件$X_{t}' \Delta^{j} X_{t} + \delta^{j \prime} X_{t} +\delta_{0}^{j} \geq 0$が成り立つ.したがって,式(43)と補題1より,次式が成り立つ.
| $$\displaystyle \lim_{T \rightarrow \infty} S_{t}^{T, j} = \displaystyle \lim_{T \rightarrow \infty} E_{t}^{\mathbb{Q}^{j}} \left[\displaystyle \int_{t}^{T} \exp\left(- \displaystyle \int_{t}^{s} r_{u}^{j} du \right) D_{s}^{j} ds \right].$$ | (44) |
上でみたように,$S_{t}^{T, j}=\exp \left(X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t \right)$となり,$E^{j}$,$f^{j}$,$g^{j}$は式(19)を満たす.当面,$E^{j}$,$f^{j}$,$g^{j}$の解は存在するとして議論を進める.$S_{t}^{T, j}=\exp \left(X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t \right)$の右辺は$T$に依存しないので,式(44)の左辺は$\displaystyle \lim_{T \rightarrow \infty} S_{t}^{T, j}=\exp \left(X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t \right)$となる.また,$D_{s}^{j} \geq 0$なので,ルベーグの単調収束定理より,式(44)の右辺は
| $$\displaystyle \lim_{T \rightarrow \infty} E_{t}^{\mathbb{Q}^{j}} \left[\displaystyle \int_{t}^{T} \exp\left(- \displaystyle \int_{t}^{s} r_{u}^{j} du \right) D_{s}^{j} ds \right] = E_{t}^{\mathbb{Q}^{j}} \left[\displaystyle \int_{t}^{\infty} \exp\left(- \displaystyle \int_{t}^{s} r_{u}^{j} du \right) D_{s}^{j} ds, \right],$$ |
となる.
以上の式展開と式(18)を踏まえると次式を得る.
| $$S_{t}^{j}=E_{t}^{\mathbb{Q}^{j}} \left[\displaystyle \int_{t}^{\infty} \exp\left(- \displaystyle \int_{t}^{s} r_{u}^{j} du \right) D_{s}^{j} ds \right] =\exp \left(X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t \right).$$ |
以下では,式(19)の解の存在についてみていく.まず,$\Psi^{j}-\Delta^{j}$は正定値対称行列と仮定しているので,式(19)の第1式は$E^{j}$に関する代数リッカチ方程式となる.行列対$(K^{j}, \Sigma)$が可制御で,$\Psi^{j}-\Delta^{j}=C'C$とするとき$(C,K^{j})$が可観測であれば,式(19)の第1式の代数リッカチ方程式は,正定値対称行列解が唯一存在する(Wonham (1968)による結果.日本語の文献では大住(2003)を参照.).
$(K^{j}, \Sigma)$の可制御性について,$t_{f}>0$のとき,
| $$\displaystyle \int_{0}^{t_{f}} e^{-K^{j}s} \Sigma \Sigma' e^{-K^{j \prime}s} ds,$$ | (45) |
が正則行列であれば,$(K^{j}, \Sigma)$は可制御であることがいえる.今,$\Sigma \Sigma'$は正定値行列と仮定しているので式(45)は正則であり,$(K^{j}, \Sigma)$は可制御である.
$(C,K^{j})$の可観測性について,
| $$\displaystyle \int_{0}^{t_{f}} e^{-K^{j}s} C' C e^{-K^{j \prime}s} ds=\displaystyle \int_{0}^{t_{0}} e^{-K^{j}s} (\Psi^{j}-\Delta^{j}) e^{-K^{j \prime}s} ds,$$ | (46) |
が正則行列であれば,$(C,K^{j})$は可観測であることがいえる.今,$\Psi^{j}-\Delta^{j}$は正定値行列と仮定しているので式(46)は正則であり,$(C, K^{j})$は可観測である.
以上より,式(19)の第1式の代数リッカチ方程式は,正定値対称行列解が唯一存在する.
式(19)の第1式の解$E^{j}$は,正定値行列なので逆行列を持つ.このことを用いると,式(19)の第2式の$f^{j}$の係数行列である$K^{j}-2\Sigma\Sigma' E^{j}$は正則行列であることが証明できる(Kikuchi (2016)参照).したがって,$f^{j}$は解を持つ.$g^j$についても,式(19)の第3式より解を持つことは明らかである.
付録C 配当ストリップス価格の導出付録Cでは,配当ストリップスの価格$DSS_{t}^{\tau, j}$の解析式を導出する.
まず,次の等式を確認しておく.
| $$S_{t}^{j} = E_{t}^{\mathbb{Q}^j} \left[ \int_{t}^{t+\tau} \exp \left( -\int_{t}^{s} r_{u}^{j} du \right) D_{s}^{j} ds \right] +E_{t}^{\mathbb{Q}^j} \left[ \exp \left( -\int_{t}^{t+\tau} r_{u}^{j} du \right) S_{t+\tau}^{j} \right].$$ | (47) |
式(47)右辺第2項を$FS_{t}^{\tau, j}$と置く.$FS_{t}^{\tau, j}$にファインマン=カックの定理を適用すると,式(7)より,次の偏微分方程式を得る.
| $$\frac{\partial FS_{t}^{\tau, j}}{\partial t} + \{ K^{j} (\theta^{j} -X_{t}) \}' \frac{\partial FS_{t}^{\tau, j}}{\partial X_{t}} + \frac{1}{2} \mathrm{Tr} \left( \Sigma \Sigma' \frac{\partial^{2} FS_{t}^{\tau, j}}{\partial X_{t} \partial X_{t}^{\prime}} \right) -r_{t}^{j} FS_{t}^{\tau,j}= 0, \ FS_{t}^{0,j} = S_{t}^{j}.$$ |
上式の解は$FS_{t}^{\tau, j}=\exp(X_{t}' E_{\tau}^{j} X_{t} + {f_{\tau}^{j \prime}} X_{t} + g_{\tau}^{j} t + h_{\tau}^{j})$と推測される.この式を上の偏微分方程式に代入し,係数比較をすると次の連立微分方程式を得る.
| $$\begin{split} \displaystyle \frac{d E_{\tau}^{j} }{ d \tau } &= -K^{j \prime} E_{\tau}^{j} - E_{\tau}^{j} K^{j} + \displaystyle 2 E_{\tau}^{j} \Sigma \Sigma' E_{\tau}^{j} - \Psi^{j}, \ E_{0}^{j}=E^{j}, \\ \displaystyle \frac{d f_{\tau}^{j}}{ d \tau } &= 2E_{\tau}^{j} K^{j} \theta^{j} - {K^{j \prime}} f_{\tau}^{j} + 2E_{\tau}^{j} \Sigma \Sigma' f_{\tau}^{j} - \varphi^{j}, \ f_{0}^{j} = f^{j}, \\ \displaystyle \frac{d h_{\tau}^{j} }{d \tau } &= (K^{j} \theta^{j})' f_{\tau}^{j} + \displaystyle \frac{1}{2} \mathrm{Tr} (\Sigma \Sigma' (2E_{\tau}^{j} + f_{\tau}^{j} f_{\tau}^{j \prime})) +g_{\tau}^{j} - \eta^{j}, \ h_{0}^{j} = 0, \\ g_{\tau}^{j} &=g^{j}. \end{split}$$ | (48) |
式(47)より,
| $$E_{t}^{\mathbb{Q}^j} \left[ \int_{t}^{t+\tau} \exp \left( -\int_{t}^{s} r_{u}^{j} du \right) D_{s}^{j} ds \right]=S_{t}^{j}-FS_{t}^{\tau, j},$$ | (49) |
なので,
| $$\begin{split} DSS_{t}^{\tau,j} &= -\displaystyle \lim_{\Delta \tau \rightarrow 0} \dfrac{FS_{t}^{\tau + \Delta \tau, j} - FS_{t}^{\tau, j}}{\Delta \tau}= -\left. \dfrac{\partial FS_{t}^{s, j}}{\partial s} \right|_{s=\tau} \\ &=- \left(X_{t}' \dfrac{d E_{\tau}^{j}}{d \tau} X_{t} + {\dfrac{d f_{\tau}^{j \prime}}{d \tau}} X_{t} +\dfrac{d g_{\tau}^{j}}{d \tau}t + \dfrac{d h_{\tau}^{j}}{d \tau} \right) \exp(X_{t}' E_{\tau}^{j} X_{t} + {f_{\tau}^{j \prime}} X_{t} + g_{\tau}^{j} t + h_{\tau}^{j}) \\ &=- \left(X_{t}' \dfrac{d E_{\tau}^{j}}{d \tau} X_{t} + {\dfrac{d f_{\tau}^{j \prime}}{d \tau}} X_{t} + \dfrac{d h_{\tau}^{j}}{d \tau} \right) \exp(X_{t}' E_{\tau}^{j} X_{t} + {f_{\tau}^{j \prime}} X_{t} + g^{j} t + h_{\tau}^{j}). \end{split}$$ | (50) |
付録D 2次ガウシアンモデルの不変変換
本付録では,式(1),(2),(5),(6),(17)から定まる2次ガウシアンモデルの不変変換について説明する.
D.1 不変変換とは状態変数$X_{t}$,状態変数を駆動するブラウン運動$W_{t}$,および,式(1),(2),(5),(6),(17)に含まれるパラメータの組を次のように表す.
| $$\left(X_{t}, W_{t}, K, \theta, \Sigma, \Psi^{j}, \varphi^{j}, \eta^{j}, \Delta^{j}, \delta^{j}, \delta_{0}^{j}, \lambda^{j}, \Lambda^{j} \right).$$ |
ここで,これらの変数やパラメータが,別の変数やパラメータに変換されるとし,変換後のモデルでは,状態変数やそれを駆動するブラウン運動,式(1),(2),(5),(6),(17)に含まれるパラメータが次のように「チルダ」を付与された形で表されるとする.
| $$\left(\tilde{X}_{t}, \tilde{W}_{t}, \tilde{K}, \tilde{\theta}, \tilde{\Sigma}, \tilde{\Psi}^{j}, \tilde{\varphi}^{j}, \tilde{\eta}^{j}, \tilde{\Delta}^{j}, \tilde{\delta}^{j}, \tilde{\delta}_{0}^{j}, \tilde{\lambda}^{j}, \tilde{\Lambda}^{j} \right).$$ |
また,式(7)に現れる$K^{j}$と$\theta^{j}$も,この変換によってそれぞれ$\tilde{K}^{j}$,$\tilde{\theta}^{j}$に変換されるものとする.
このとき,次式が成り立つ場合に,上記の変換を「不変変換」と呼ぶ.
| $$\begin{split} P_{t}^{\tau,j} &= \exp(X_{t}' A_{\tau}^{j} X_{t} + b_{\tau}^{j \prime} X_{t} + c_{\tau}^{j}) = \exp(\tilde{X}_{t}' \tilde{A}_{\tau}^{j} \tilde{X}_{t} + \tilde{b}_{\tau}^{j \prime} \tilde{X}_{t} + \tilde{c}_{\tau}^{j}),\\ S_{t}^{j} &= \exp(X_{t}' E^{j} X_{t} + f^{j \prime} X_{t} + g^{j} t) = \exp(\tilde{X}_{t}' \tilde{E}^{j} \tilde{X}_{t} + \tilde{f}^{j \prime} \tilde{X}_{t} + \tilde{g}^{j} t). \end{split}$$ | (51) |
ここで,式(51)における$(A_{\tau}^{j}, b_{\tau}^{j}, c_{\tau}^{j})$は式(10)の解,$(E^{j}, f^{j}, g^{j})$は式(19)の解である.また,$(\tilde{A}_{\tau}^{j}, \tilde{b}_{\tau}^{j}, \tilde{c}_{\tau}^{j})$は式(10)の全ての係数にチルダを付けた場合の解,$(\tilde{E}^{j}, \tilde{f}^{j}, \tilde{g}^{j})$は式(19)の全ての係数にチルダを付けた場合の解である.
D.2 状態変数のアフィン変換に伴う不変変換状態変数のアフィン変換に伴う不変変換を明らかにする.$\gamma + \Gamma X_t$を$\tilde{X}_t$と置く.すなわち,$\tilde{X}_t$は$X_t$ のアフィン変換によって得られる変数である.なお,$\Gamma$は正則行列とする.
$\tilde{X}_t$の$\mathbb{P}$の下での確率過程は,式(1)に$X_t = \Gamma^{-1}(\tilde{X}_t - \gamma)$を代入して整理すると,
| $$d \tilde{X}_t = \Gamma K \Gamma^{-1} \left( \Gamma \theta + \gamma - \tilde{X}_t \right) dt + \Gamma \Sigma d W_t,$$ | (52) |
となる.ここで,$\Gamma K \Gamma^{-1}$を $\tilde{K}$,$\Gamma \theta + \gamma$ を $\tilde{\theta}$,$\Gamma \Sigma$ を $\tilde{\Sigma}$,$W_{t}$ を $\tilde{W}_{t}$と置くと,
| $$d \tilde{X}_t = \tilde{K} \left( \tilde{\theta} - \tilde{X}_t \right) dt + \tilde{\Sigma} d \tilde{W}_{t},$$ | (53) |
と表される.式(1)では,$K$の固有値は全て正の値をとることを仮定していた.$\tilde{K} = \Gamma K \Gamma^{-1}$は,$K$と同じ固有値を持つことが簡単な計算により確かめられる.したがって,$\tilde{K}$も全ての固有値が正の値を取ることが分かる.また,式(53)の右辺のボラティリティ項$\tilde{\Sigma} = \Gamma \Sigma$に関して,分散共分散行列$\tilde{\Sigma} \tilde{\Sigma}' = \Gamma \Sigma \Sigma' \Gamma'$は,$\Sigma \Sigma'$が正定値行列より,やはり正定値行列になる.以上より,状態変数のアフィン変換によって,状態変数の確率過程の設定は変化しないことが分かる.
次に,式(2)で定義されているショートレート$r_{t}^{j}$を$\tilde{X}_t$を用いて書き下すと,
| $$r_{t}^{j} = \tilde{X}_t' {\Gamma'}^{-1} \Psi^{j} \Gamma^{-1} \tilde{X}_t +(-2 \gamma' {\Gamma'}^{-1} \Psi^{j} \Gamma^{-1} +\varphi^{j \prime} \Gamma^{-1} )\tilde{X}_{t} + \gamma' {\Gamma'}^{-1} \Psi^{j} \Gamma^{-1} \gamma - \varphi^{j \prime} \Gamma^{-1} \gamma + \eta^{j}, $$ | (54) |
となる.ここで,
| $$\begin{split} \tilde{\Psi}^{j}&={\Gamma'}^{-1} \Psi^{j} \Gamma^{-1}, \\ \tilde{\varphi}^{j}&={\Gamma'}^{-1}(-2\Psi^{j}\Gamma^{-1}\gamma+\varphi^{j}), \\ \tilde{\eta}^{j}&=\gamma' {\Gamma'}^{-1} \Psi^{j} \Gamma^{-1} \gamma - \varphi^{j \prime} \Gamma^{-1} \gamma + \eta^{j}, \end{split}$$ |
と置くと,$r_{t}^{j}=\tilde{X}_{t}' \tilde{\Psi}^{j}\tilde{X}_t +\tilde{\varphi}^{j \prime}\tilde{X}_{t} + \tilde{\eta}^{j}$である.なお,$\Psi^{j}$を正定値対称行列と仮定していたので,$\tilde{\Psi}^{j}$も正定値対称行列である.このことから,状態変数のアフィン変換によって式(2)の設定は変化しないことが分かる.
次に,式(17)において株式の配当利回りに相当する$\dfrac{D_{t}}{S_{t}}=X_{t}' \Delta^{j} X_{t} + \delta' X_{t} + \delta_{0}$を$\tilde{X}_t$を用いて書き下す.
| $$\begin{split} \tilde{\Delta}^{j}&={\Gamma'}^{-1} \Delta^{j} \Gamma^{-1}, \\ \tilde{\delta}^{j}&={\Gamma'}^{-1}(-2\Delta^{j}\Gamma^{-1}\gamma+\delta^{j}), \\ \tilde{\delta}_{0}^{j}&=\gamma' {\Gamma'}^{-1} \Delta^{j} \Gamma^{-1} \gamma - \delta^{j \prime} \Gamma^{-1} \gamma + \delta_{0}^{j}, \end{split}$$ |
と置くと,
| $$\dfrac{D_{t}}{S_{t}}=X_{t}' \Delta^{j} X_{t} + \delta^{j \prime} X_{t} + \delta_{0}^{j}=\tilde{X}_{t}' \tilde{\Delta}^{j} \tilde{X}_{t} + \tilde{\delta}_{0}^{j \prime} \tilde{X}_{t} + \tilde{\delta}_{0}^{j},$$ | (55) |
となることが分かる.なお,$\Delta^{j}$を正定値対称行列と仮定していたので,$\tilde{\Delta}^{j}$も正定値対称行列である.このことから,状態変数のアフィン変換によって式(17)の設定は変らないことが分かる.
リスクの市場価格に係る式(6)のパラメータに関して,$\tilde{\lambda}^{j}=\lambda^{j}-\Lambda^{j}\Gamma^{-1}\gamma$,$\tilde{\Lambda}^{j}=\Lambda^{j}\Gamma^{-1}$と置くと,
| $$\lambda^{j} + \Lambda^{j} X_{t} = \tilde{\lambda}^{j} + \tilde{\Lambda}^{j} \tilde{X}_{t},$$ | (56) |
である.
上記の状態変数,ブラウン運動,パラメータの変換によって得られるモデル
| $$\left(\tilde{X}_{t}, \tilde{W}_{t}, \tilde{K}, \tilde{\theta}, \tilde{\Sigma}, \tilde{\Psi}^{j}, \tilde{\varphi}^{j}, \tilde{\eta}^{j}, \tilde{\Delta}^{j}, \tilde{\delta}^{j}, \tilde{\delta}_{0}^{j}, \tilde{\lambda}^{j}, \tilde{\Lambda}^{j} \right),$$ |
と変換前のモデルについて,式(51)が成立すること,すなわち,変換前後で債券価格と株価が一致することは多少の計算により確認できる.
D.3 ブラウン運動の回転変換に伴う不変変換状態変数のアフィン変換に伴う不変変換に続き,ブラウン運動の回転変換に伴う不変変換を明らかにする.標準ブラウン運動 $W_t$に直交行列$U$を左から乗じた$UW_t$ は,再び$\mathbb{P}$における標準ブラウン運動になる.$UW_{t}$を$\tilde{W}_t$と置く.ここで,リスクの市場価格を定めた式である式(5),(6)について,$\tilde{W}_t$を用いて書き下すと,
| $$d(U{W}_{t}^{j}) = d(UW_{t}) + (U\lambda^{j} + U\Lambda^{j} X_{t}) dt = d \tilde{W}_{t} + (U\lambda^{j} + U\Lambda^{j} X_{t}) dt,$$ | (57) |
となる.ここで,$UW_{t}^{j}$を$\tilde{W}_{t}^{j}$と置くと,これは$\mathbb{Q}^{j}$における標準ブラウン運動に従う.また,$\tilde{\lambda}^{j} = U\lambda^{j}$,$\tilde{\Lambda}^{j} = U\Lambda^{j}$と置くと,式(57)は,
| $$d\tilde{W}_{t}^{j} = d\tilde{W}_{t} + (\tilde{\lambda}^{j} + \tilde{\Lambda}^{j} X_{t}) dt,$$ | (58) |
となるため,ブラウン運動の回転変換後も,リスクの市場価格は本質的アフィンを維持することが分かる.
式(1)を$\tilde{W}_t$を用いて書き下すと,
| $$dX_{t} = K(\theta - X_{t})dt + \Sigma U^{-1} d(UW_{t})=K(\theta - X_{t})dt + \Sigma U^{-1} d \tilde{W}_{t},$$ | (59) |
となる.ここで,$\tilde{\Sigma} = \Sigma U^{-1}$と置く.
ブラウン運動$W_{t}$の回転に伴い,$\tilde{W}_{t}=UW_{t}$,$\tilde{\lambda}^{j} = U\lambda^{j}$,$\tilde{\Lambda}^{j} = U\Lambda^{j}$,$\tilde{\Sigma} = \Sigma U^{-1}$と置いたが,それ以外のパラメータについては変換前後で不変とする.また,$\tilde{X}_{t}=X_{t}$である.以上の変換を仮定した場合,式(7)に関連するパラメータ$\tilde{K}^{j}$と$\tilde{\theta}^{j}$は次のように計算される.
| $$\begin{align*} \tilde{K}^{j}&=\tilde{K}+\tilde{\Sigma}\tilde{\Lambda}^{j}=K+\Sigma U^{-1} U \Lambda^{j} = K + \Sigma \Lambda = K^{j},\\ \tilde{K}^{j}\tilde{\theta}^{j} &= \tilde{K}\tilde{\theta}-\tilde{\Sigma}\tilde{\lambda}^{j} = K \theta - \Sigma U^{-1} U \lambda^{j} = K \theta -\Sigma \lambda = K^{j}\theta^{j}. \end{align*}$$ |
これより,$\tilde{K}^{j}=K^{j}$,$\tilde{\theta}^{j}=\theta^{j}$が成り立つことが分かる.
以上の変換のもとで,式(10)の解$(A_{\tau}^{j}, b_{\tau}^{j}, c_{\tau}^{j})$は,式(10)の全ての係数にチルダを付けた場合の方程式の解$(\tilde{A}_{\tau}^{j}, \tilde{b}_{\tau}^{j}, \tilde{c}_{\tau}^{j})$と一致する.これは,$UU'$が単位行列に等しいことから確認できる.さらに,式(19)の解$(E^{j}, f^{j}, g^{j})$も,式(19)の全ての係数にチルダを付けた場合の解$(\tilde{E}^{j}, \tilde{f}^{j}, \tilde{g}^{j})$と一致することが確認される.以上より,ブラウン運動の回転に伴う上記の変換の下,式(51)が成立する.
D.4 $K$を下三角行列,$\theta$を零ベクトル,$\Sigma$を単位行列に変換できること式(52)において$\Gamma = \Sigma^{-1}$,$\gamma = -\Gamma \theta$と取ると,
| $$d \tilde{X}_t = -\Sigma^{-1} K \Sigma \tilde{X}_t dt + dW_t = -\tilde{K} \tilde{X}_t dt + d\tilde{W}_t,$$ | (60) |
となる.
ここで,$\tilde{K}=\Sigma^{-1} K \Sigma$の固有値は$K$の固有値と一致する.$K$の固有値は全て正であると仮定していたので,$\tilde{K}$の固有値も全て正である.これより,ある直交行列$P$が存在して$P'\tilde{K}P$を下三角行列に変形することができる.このことと式(60)より,
| $$d(P' \tilde{X}_t) = -P' \tilde{K} P (P' \tilde{X}_t) dt + P' dW_t,$$ |
となる.ここで,$P' \tilde{X}_t$ を $\hat{X}_t$,下三角行列である $P' \tilde{K} P$ を $\hat{K}$,$P' dW_t$ を $d\hat{W}_{t}$ と置くと,
| $$d \hat{X}_t = -\hat{K} \hat{X}_t dt + P' dW_t= -\hat{K} \hat{X}_t dt + d\hat{W}_{t}.$$ |
以上の議論より,状態変数が$\mathbb{P}$の下で従う確率過程のボラティリティ項は単位行列に変換することができるため,状態変数が$\mathbb{P}$の下での確率過程を下三角行列$K$を用いて,
| $$dX_t = -K X_t dt + dW_{t},$$ | (61) |
と仮定してよい.ここで,$K$の固有値は全て正であると仮定しているため,上記の下三角行列$K$の対角成分は全て正である.