円運動モデルによるNICSの定量的計算

Abstract

環状π電子系化合物の芳香族性の指標として使われる核磁気遮蔽定数(-NICS)のモデル計算を紹介する．実在系では化合物ごとに異なる複雑な条件がNICSの議論を複雑にしている．化合物固有の複雑性を避けて，基本原理だけが浮き出るようにするために円運動モデルを採用した．更に，古典的・概念的な記述を避けるため，フレミングの左手の法則やアンペールの法則などは使わず，円周上の電子の運動にシュレーディンガー方程式を適用した．NICS値をこのモデルの範囲内で定量的に計算した結果，ベンゼンのNICS値と半定量的な一致を得た．更に，ab-initio MO計算の結果を示し，モデル計算とab-initio計算を数値的に比較・検証した．

Translated Abstract

The nucleus-independent chemical shift (NICS) of benzene is calculated using a one-dimensional ring model. In a real compound, an individual feature contributes to the NICS and it makes an intuitive understanding of the NICS complicate and difficult. We can avoid this complexity by using an extremely simple model. To overcome a classical and naive understanding such as the Fleming's left hand rule or the Ampère's circuital law, we apply the Schrödinger equation to an electron on a one-dimensional ring, and evaluate the NICS quantitatively in a framework of this ring model, using both Ramsey's equation and Pople's method. We also compare these results with the ab-initio MO calculations. From these results, we discuss about the diamagnetic and paramagnetic terms (diatropic- and paratropic-type currents) of NICS.

1 はじめに

環状π電子系化合物の芳香族性を議論する際，しばしばNucleus-Independent Chemical Shift (NICS)が使われる [1]．初期のNICSは任意の位置に置いた仮想的な原子核に対する核磁気遮蔽定数を計算し，その符号を逆にした値として定義される．環状π電子系化合物のNICSは芳香族性・反芳香族性の基準として多くの議論がなされてきた [2,3,4]．一方では観測値でないために芳香族性の評価に使うことを疑問視する論文もある [5]．NICSを直観的に説明するために誘起電流が使われる．芳香族性化合物では環の内側で外部磁場を遮蔽するように反磁性電流(diatropic電流)が流れ，反芳香族性化合物ではその逆向きに常磁性環電流(paratropic電流)が流れると考えられている [6]．

マクロな古典電磁気学において，磁気遮蔽はLenzの法則そのものである．Lenzの法則によれば，外部磁場によって誘導電流が発生する場合，誘導電流はその原因である外部磁場を弱める方向に流れる．従って，誘導電流は上述の反磁性電流であり，核磁気遮蔽の正値(高磁場シフト)，つまりNICSに換算すると負値を与える．一方，常磁性環電流は量子力学的効果により外部磁場を増加させる方向に流れ，NICSの正値を与える．

また，量子化学計算で使われるGauge-Including Atomic Orbital (GIAO) [7]はNMR化学シフトの計算精度を向上させたが，その一方ではGIAO補正値はNICS値の直観的理解を妨げている．

本解説記事では，単純化したモデルによる核磁気遮蔽定数(-NICS)の数値計算を紹介する．実在系では化合物ごとに異なる種々の現象が議論を複雑にしている．化合物固有の複雑性を避けて，基本原理だけが浮き出るようにするために円運動モデルを採用する．但し，「磁場が作用すれば環電流が流れるに違いない」といった直感的な議論は避けたい．そこで，少々やっかいであるが，円周上の電子の運動にシュレーディンガー方程式を適用する．そしてNICSをこのモデルの範囲内で定量的に計算し，その結果から直観的な理解を得たい．2節で核磁気遮蔽定数とNICSを定義し，3節と4節で円周上を運動する電子によるNICSを求める．5節は環電流とNICSの対応を議論する．最後の6節では円運動モデルに類似した分子系(水素原子を円周上に12個並べた系)のab-initio計算の例を示し，モデル計算とab-initio計算を数値的に比較・検証する．7節は余談である．

2 核磁気遮蔽定数とNICSの定義

均一で時間変化しない外部磁束密度$B_0$と核磁気双極子${\mu }_{\text{N}}$の相互作用エネルギーは両者の内積$\Delta E=-{\mu }_{\text{N}}{B}_0$である．$B_0$と${\mu }_{\text{N}}$が同じ方向のときに安定化するのでマイナス符号を付す．原子核の周囲には電子が存在するので誘起磁束密度$B_{Induced}$が発生し，原子核$\text{N}$が感じる磁束密度は次式のように減少する．   

$\Delta E=-{\mu }_{\text{N}}(B_0-B_{Induced})=-{\mu }_{\text{N}}\left(1-\frac{B_{Induced}}{B_0}\right)B_0$

$B_0$が減少する割合を核磁気遮蔽定数${\sigma }_{\text{N}}$と定義する．   

${\sigma }_{\text{N}}=\frac{B_{Induced}}{B_0}$(1)

${\sigma }_{\text{N}}$を使うとエネルギー変化$\Delta E$は次式となる．   

$\Delta E=-{\mu }_{\text{N}}(1-{\sigma }_{\text{N}})B_0$(2)

特に断らなければ太字立体(上式では$B_{Induced}$，$B_0$及び${\mu }_{\text{N}}$)はベクトルである．従って${\sigma }_{\text{N}}$は3×3のテンソル量，1は3×3の単位行列である．${\sigma }_{\text{N}}$の各成分は${\sigma }_{\text{N}tu}={\sigma }_{\text{N}ut}$($t,u=x,y,z$)が成立するので独立な成分は6個である．溶液中では分子回転のため対角項成分の平均値である等方性項${\sigma }_{\text{N}iso}$のみが観測される．   

${\sigma }_{\text{N}iso}=\frac{{\sigma }_{\text{N}xx}+{\sigma }_{\text{N}yy}+{\sigma }_{\text{N}zz}}{3}$

${\sigma }_{\text{N}iso}$の±符号を逆にした値をNICS，そして，${\sigma }_{\text{N}zz}$の±符号を逆にした値をNICSzzと定義する．

${\sigma }_{\text{N}}$の計算方法に関する説明には，しばしばPopleの方法とRamseyの式が引き合いに出される．両者は出発点の違いであって，他の前提条件が同じならば計算結果も同じである．Popleは，$B_0$で誘起された電流密度$j$を使って研究を展開した [8]．$j$は量子力学的な確率密度流に電子の電荷($-e$)を乗じて得られる．磁場下の運動量演算子$\hat{\pi }$と分子軌道${\psi }_k\left(B_0\right)$($k=1,2,3,\cdot \cdot \cdot$)を使うと$j$は次式となる．   

$j=\frac{-e}{2m_e}\sum _{k=1}^{occ}\left[{\psi }_k{\left(B_0\right)}^{*}\hat{\pi }{\psi }_k\left(B_0\right)+{\psi }_k\left(B_0\right){\hat{\pi }}^{*}{\psi }_k{\left(B_0\right)}^{*}\right]$(3)

ここで$\hat{\pi }=\hat{p}+eA$であり，$\hat{p}$は運動量演算子，Aは磁場のベクトルポテンシャルである．電流$i$から$B_{Induced}$を計算する場合にはビオ・サバールの式を使う．微小長さ$ds$の電流$i$が位置$r$に作る磁束密度は$dB$である．   

$dB=\frac{{\mu }_0}{4\pi }\frac{i\times r}{r^3}ds$(4)

一方，最近の量子化学の論文ではRamseyの式から${\sigma }_{\text{N}}$の計算式を導出している [9]．   

${\sigma }_{\text{N}}={\frac{{\partial }^{2}E}{\partial {\mu }_{\text{N}}\partial B_0}|}_{{\mu }_{\text{N}}=B_0=0}$(5)

$E$は量子化学計算で得たエネルギーである．Ramseyの式(5)は現象論的な(2)式から推測できる．

上式(3)~(5)を計算するには$B_0$と${\mu }_{\text{N}}$に依存するエネルギー$E(B_0,{\mu }_{\text{N}})$や${\psi }_{0k}\left(B_0\right)$が必要である．まず，$B_0$と${\mu }_{\text{N}}$を考慮したエネルギー演算子$\hat{F}$(Fock演算子)をそれらのべき乗で展開する．   

$\hat{F}={\hat{F}}^{\left(0\right)}+{\hat{F}}^{(1,0)}{B}_0+{\hat{F}}^{(0,1)}{\mu }_{\text{N}}+{\mu }_{\text{N}}{\hat{F}}^{(1,1)}{B}_0$

上式中の${\hat{F}}^{(n,m)}$は$B_0^n{\mu }_{\text{N}}^m$の係数である．$B_0^2$と${\mu }_{\text{N}}^2$などの高次項は${\sigma }_{\text{N}}$の計算には不要なので省略した．無磁場の分子軌道方程式${\hat{F}}^{\left(0\right)}{\psi }_k={\epsilon }_k^{\left(0\right)}{\psi }_k$の軌道エネルギー$\epsilon {}_k{}^{\left(0\right)}$と波動関数${\psi }_{0k}(k=0,1,2,\cdot \cdot \cdot )$があれば，(5)式を2次摂動論で与えることができる．   

${\sigma }_{\text{N}}=\sum _k^{occ}⟨{\psi }_k\left|{\hat{F}}^{(1,1)}\right|{\psi }_k⟩-\sum _k^{occ}\sum _a^{unocc}\frac{⟨{\psi }_a\left|{\hat{F}}^{(1,0)}\right|{\psi }_k⟩⟨{\psi }_k\left|{\hat{F}}^{(0,1)}\right|{\psi }_a⟩}{{\epsilon }_a^{\left(0\right)}-{\epsilon }_k^{\left(0\right)}}+c.c.$(6)

ここで$c.c.$は前項の複素共役である．上式の第1項は反磁性(diamagnetic)項であり，基底状態の占有分子軌道$\left\{{\psi }_k\right\}$だけを含む．第2項は常磁性(paramagnetic)項であり，波動関数の磁場応答，つまり非占有軌道$\left\{{\psi }_a\right\}$の混入，によって生じる．$B_0$が作用することで変化した分子軌道${\psi }_k\left(B_0\right)$とその微分式も1次摂動論の範囲で示すことができる．   

${\psi }_k\left(B_0\right)={\psi }_k+B_0\sum _a^{unocc}\frac{⟨{\psi }_a\left|{\hat{F}}^{(1,0)}\right|{\psi }_k⟩}{{\epsilon }_k^{\left(0\right)}-{\epsilon }_a^{\left(0\right)}}{\psi }_a$(7)

，   

$\frac{d{\psi }_k\left(B_0\right)}{d{B}_0}=\sum _a^{unocc}\frac{⟨{\psi }_a\left|{\hat{F}}^{(1,0)}\right|{\psi }_k⟩}{{\epsilon }_k^{\left(0\right)}-{\epsilon }_a^{\left(0\right)}}{\psi }_a$(8)

(6)~(8)式における積分値$⟨{\psi }_a\left|{\hat{F}}^{(1,0)}\right|{\psi }_k⟩$が非ゼロとなる遷移$k\to a$は磁気的許容遷移である．以上で次節以降の準備は完了した．最後に必要な物理定数を纏めておく．

$-e$:電子の電荷， ${\epsilon }_0$:真空の誘電率， ${\mu }_0$:真空の透磁率，

$m_e$:電子の質量， $\hslash$:換算プランク定数($\hslash \equiv h/2\pi$)， $c$:光速度

3 円運動モデルI:(4n+2)電子系

$xy$平面に置いた半径$r$の円周上を運動する電子を考える．Figure 1に示すような角度$\varphi$を変数とする1次元モデルをモデルIとする．ベンゼンのπ電子を模した最も簡単なモデル系と云える．このモデルIは(4n+2)電子系のみを想定している．

Figure 1.

 Electron on a one-dimensional ring as a model of π-electrons of benzene (model-I).

Figure 1右の系に均一な静磁束密度$B_0$をz軸方向に作用させ，仮想的な核磁気双極子${\mu }_{\text{N}}$をz軸へ向けて円の中心に配置する．電子-電子間の電気的クーロン反発は考慮しない．この設定で円中央の核磁気遮蔽定数${\sigma }_{zz}$を計算し，その符号を逆にすればNICSzz値となる．

先ず，質量$m_e$の電子が円周を運動するときのシュレーディンガー方程式を次式とする．   

$\frac{{({\hat{p}}_{\varphi }+e{A}_{\varphi })}^2}{2m_e}\psi \left(\varphi \right)=E\psi \left(\varphi \right)$

${\hat{p}}_{\varphi }$は円周上の角運動量である．$A_{\varphi }$はベクトルポテンシャルであり，$B_0$と${\mu }_{\text{N}}$を使って次式となる．   

$A_{\varphi }=\frac{1}{2}{B}_{0}r+\frac{{\mu }_0}{4\pi }\frac{{\mu }_{\text{N}}}{r^2}$

上式を展開して$B_0$と${\mu }_{\text{N}}$のそれぞれ1次の項までを拾うと，前節の(6)~(8)式に必要な具体的な形を得る．   

$\left({\hat{F}}^{\left(0\right)}+{\hat{F}}_{}^{(1,0)}{B}_0+{\hat{F}}_{}^{(0,1)}{\mu }_{\text{N}}+{\hat{F}}_{}^{(1,1)}{B}_0{\mu }_{\text{N}}\right)\psi \left(\varphi \right)=E(B_0,{\mu }_{\text{N}})\psi \left(\varphi \right)$(9)

  

${\hat{F}}_0=\frac{{\hat{p}}_{\varphi }^2}{2m_e}=-\frac{{\hslash }^2}{2m_e{r}^2}\frac{d^2}{d{\varphi }^2}$

  

${\hat{F}}_{}^{(1,0)}=\frac{e}{2m_e}{\hat{L}}_z=\frac{e}{2m_e}\frac{\hslash }{i}\frac{d}{d\varphi }$

  

${\hat{F}}_{}^{(0,1)}=\frac{e}{m_e}\frac{{\mu }_0}{4\pi }\frac{{\hat{L}}_z}{r^3}=\frac{e}{m_e{r}^3}\frac{{\mu }_0}{4\pi }\frac{\hslash }{i}\frac{d}{d\varphi }$

  

${\hat{F}}_{}^{(1,1)}=\frac{e^2}{m_e}\frac{{\mu }_0}{4\pi }\frac{1}{r}$

${\hat{L}}_z$はz軸方向の角運動量，${\hat{F}}_{}^{(1,0)}$は磁場と電子の相互作用項(Zeeman項)，${\hat{F}}_{}^{(0,1)}$は核磁気双極子と電子の相互作用項，${\hat{F}}_{}^{(1,1)}$電子を介した磁場と核磁気双極子の間接的相互作用を与える．境界条件$\psi \left(\varphi \right)=\psi (\varphi +2\pi )$のもとで(9)式は直ちに解ける．   

${\psi }_m\left(\varphi \right)=\frac{1}{\sqrt{2\pi }}{e}^{im\varphi }$(10)

  

$E_m(B_0,{\mu }_{\text{N}})=E_m^{\left(0\right)}-m\frac{e\hslash }{m_e}\left(\frac{1}{2}{B}_0+\frac{{\mu }_0}{4\pi }\frac{1}{r^3}{\mu }_{\text{N}}\right)+\frac{e^2}{m_e}\frac{{\mu }_0}{4\pi }\frac{1}{r}{B}_0{\mu }_{\text{N}}$(11)

ここで，$m$は原子系で使う磁気量子数$m=0,\pm 1,\pm 2,\cdot \cdot \cdot$と同等であり，本解説でも磁気量子数と呼ぶことにする．また，(11)式第1項である無磁場のエネルギー$E_m^{\left(0\right)}$は次式となる．   

$E_m^{\left(0\right)}=\frac{m^2{\hslash }^2}{2m_e{r}^2}$

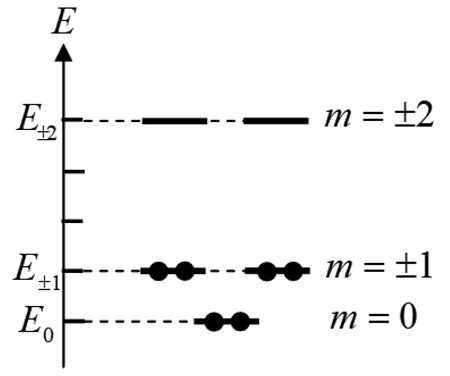
$E_m^{\left(0\right)}$の低エネルギー部分をFigure 2に示す．電子スピンを考慮すると状態${\psi }_m$は2電子を収容するので，(4n+2)電子系が閉殻系となる．Figure 2ではベンゼンの電子配置に対応させるため6個の電子を占有させた．

Figure 2.

 Energy levels $E_m^{\left(0\right)}$($m=0,\pm 1,\pm 2$) and occupancy of electrons in model-I without electric field.

因みに，$r=1.4$Åとして$m=\pm 1$から$m=\pm 2$への遷移エネルギーを計算すると$5.83\text{eV}$となり，観測値$\text{4}\text{.9}\text{eV}$~$6.2\text{eV}$ [10]と程々に一致する．この結果は，モデルIがベンゼンのπ電子系モデルとして一定の妥当性があることを示している．

(11)式をRamseyの式(5)へ代入すると磁気量子数ごとの核磁気遮蔽定数のzz成分${\sigma }_m^{\left(\text{I}\right)}$を得る．この${\sigma }_m^{\left(\text{I}\right)}$は$m$に依存しないので電子数を乗じれば分子全体の核磁気遮蔽定数${\sigma }_{}^{\left(\text{I}\right)}$を得る．   

${\sigma }_{}^{\left(\text{I}\right)}={\sigma }_m^{\left(\text{I}\right)}$

×(電子数)

$=\frac{e^2}{m_e}\frac{{\mu }_0}{4\pi }\frac{1}{r}$

×(電子数)

モデルIでは(10)式のように波動関数が磁場に依存しないので常磁性項は発生しない．

${\sigma }_m^{\left(\text{I}\right)}$を数値計算する為に原子単位系($e=1$，$m_e=1$，$\hslash =1$，$4\pi {\epsilon }_0=1$)に変換して，物理法則${\epsilon }_0{\mu }_0=c^{-2}$を考慮すると次式を得る．   

${\sigma }_m^{\left(\text{I}\right)}=c^{-2}\frac{1}{r}$

原子単位系では$c\approx 137$，$r=1.4$Åは$r=1.4÷0.529177\text{bohr}$となるので上式の計算値は約20ppmとなる．半径$r=1.4$Åの円周に1電子が分布するとNICSzz = −20ppmとなることは参考値として有用である．6π電子系のベンゼンならば6倍してNICSzz =−120 ppmとなる．

4 円運動モデルII

(4n)電子系に適用できるモデルを作る．実在の(4n)π電子系化合物は対称性の低下などが原因で，軌道エネルギーの縮退が解けている．一方で，波動関数の基本的な性質(例えばnodeの数など)は概ね保持されている．このような微妙な状況をモデル化する．簡便な方法として，モデルIの$E_{+m}$と$E_{-m}$にそれぞれ微小なエネルギー項$\Delta$を加えて人為的に縮退を崩す．   

$E_{+m}\to E_{+m}+\Delta$

，   

$E_{-m}\to E_{-m}-\Delta$

，   

$\Delta =E_1\xi =\frac{{\hslash }^2}{2m_e{r}^2}\xi$

ここで$\xi$は縮退が崩れている度合いを$E_1$との比として示す無次元量である．$\xi \to 0$の場合は$+m$と$-m$は縮退する．4個の電子が占有した状態をFigure 3に示す(便宜上$m=-1$をHOMO，$m=+1$をLUMOとした)．このモデルIIは任意の閉殻系，つまり(2n)電子系に適用できる．但し，電子スピンの磁気遮蔽を考慮していないので開殻系に使うことは避ける．

Figure 3.

 Energy levels and occupancy of electrons in model-II ($\xi =0.20$)

モデルIIでは，無摂動系の波動関数${\phi }_0$として(10)式の代わりに三角関数を使う．厳密ではないが，この表記は対称性が僅かに崩れた波動関数の代用である．   

${\phi }_0\left(\varphi \right)=\frac{1}{\sqrt{2\pi }}$(13)

  

${\phi }_{+m}\left(\varphi \right)=\frac{1}{\sqrt{\pi }}\sin \left(m\varphi \right)$(14)

，

${\phi }_{-m}\left(\varphi \right)=\frac{1}{\sqrt{\pi }}\cos \left(m\varphi \right)$(14)

(

$m=1,2,\cdot \cdot \cdot$(14)

) ${\phi }_m$と${\hat{F}}_{}^{(1,0)}$，${\hat{F}}_{}^{(0,1)}$，${\hat{F}}_{}^{(1,1)}$を(6)式に代入すると核磁気遮蔽定数の計算式を得る．   

${\sigma }_{\text{N}zz}={\sigma }_{\text{N}zz}^{dia}+{\sigma }_{\text{N}zz}^{para}$

  

$\begin{array}{c}{\sigma }_{\text{N}zz}^{dia}=\sum _k^{occ}⟨{\psi }_k\left|{\hat{F}}^{(1,1)}\right|{\psi }_k⟩\\ {\sigma }_{\text{N}zz}^{para}=-\sum _k^{occ}\sum _a^{unocc}\frac{⟨{\psi }_a\left|{\hat{F}}^{(1,0)}\right|{\psi }_k⟩⟨{\psi }_k\left|{\hat{F}}^{(0,1)}\right|{\psi }_a⟩}{{\epsilon }_a^{\left(0\right)}-{\epsilon }_k^{\left(0\right)}}+c.c.\end{array}$

上式の第1項${\sigma }_{\text{N}zz}^{dia}$は反磁性項で全ての軌道で非ゼロの値を持つ．第2項${\sigma }_{\text{N}zz}^{para}$の常磁性項は，${\hat{F}}^{(1,0)}$の積分値が${\phi }_{-m}$と${\phi }_{+m}$の間でのみ値を持つ(つまり${\phi }_{-m}$→${\phi }_{+m}$が磁気的許容遷移である)ことを考慮すると，モデルIIの磁気遮蔽定数${\sigma }_{}^{\left(\text{II}\right)}$は(4n+2)電子系と(4n)電子系で式が異なる．

(a) (4n+2)電子系   

${\sigma }_{}^{\left(\text{II}\right)}={\sigma }_{}^{\left(\text{I}\right)}$

(b) (4n)電子系 ($\pm m$はHOMOとLUMO)   

${\sigma }_{}^{\left(\text{II}\right)}={\sigma }_{}^{\left(\text{I}\right)}-\frac{e^2}{m_e}\frac{{\mu }_0}{4\pi }\frac{1}{r}\frac{m^2}{\xi }\times 2$

(b)の場合，第2項は常磁性項である．この常磁性項は$m^2$に比例し，$\xi$(つまりHOMO-LUMOのエネルギー間隔)に反比例している．$\xi \to 0$のとき$\pm m$のエネルギーが縮退し，${\sigma }_{}^{\left(\text{II}\right)}$は理論上無限大となる．数値的には，$m=1$かつ$\xi =0.40$と仮定すると常磁性項は約-100 ppmとなる．4電子系の場合に(b)の式を使うと${\sigma }_{}^{\left(\text{II}\right)}$=-20 ppm (NICSzz = 20 ppm) となる．

5 誘起電流

Ramseyの式で計算した核磁気遮蔽定数とPopleの誘起電流との対応を検討する．モデルIIの設定を引き継ぎ(4n)電子系とする． (7)式で占有軌道を$k=-m$とすると，磁気的許容遷移は$k=-m$がHOMO，かつ，$a=+m$がLUMOの場合にのみ生じる．この場合，微小な$B_0$による波動関数${\phi }_{-m}(\varphi ;B_0)$は次式となる．   

${\phi }_{-m}(\varphi ;B_0)={\phi }_{-m}\left(\varphi \right)-B_0\frac{⟨{\phi }_m\left|{\hat{F}}_{}^{(1,0)}\right|{\phi }_{-m}⟩}{2\Delta }{\phi }_{+m}\left(\varphi \right)$

  

$={\phi }_{-m}\left(\varphi \right)-i\frac{me}{2\hslash }\frac{B_0}{\xi }{r}^2{\phi }_{+m}\left(\varphi \right)$

$i$は虚数単位であり，磁場が作用すると実数関数${\phi }_{-m}$へ${\phi }_{+m}$を含む虚数項が加わり，この虚数項が磁束密度に比例する変化を与える．電流密度の式(3)から，HOMO${\phi }_{-m}$が作る電流密度$j_{-m}$は次式となる．   

$\begin{array}{c}{j}_{-m}=\frac{-e}{2m_e}\left({\phi }_{-m}^{*}(\varphi ;B_0)({\hat{p}}_{\varphi }+e{A}_{\varphi }){\phi }_{-m}(\varphi ;B_0)+{\phi }_{-m}(\varphi ;B_0){({\hat{p}}_{\varphi }+e{A}_{\varphi })}^{*}{\phi }_{-m}^{*}(\varphi ;B_0)\right)\\ =j_{-m}^{dia}+j_{-m}^{para}\end{array}$

  

$\begin{array}{c}{j}_{-m}^{dia}=-\frac{e^{2}r}{m_e}{\left|{\phi }_{-m}\left(\varphi \right)\right|}^2{B}_0\\ j_{-m}^{para}=-\frac{e^{2}r}{m_e}\frac{{\left|{\phi }_{+m}\left(\varphi \right)\right|}^2+{\left|{\phi }_{-m}\left(\varphi \right)\right|}^2}{2}\frac{m^2}{\xi }{B}_0\end{array}$

第1項$j_{-m}^{dia}$はdiatropic電流であり，$k=-m$だけでなく全ての占有軌道${\phi }_k$から生じる．第2項$j_{-m}^{para}$はparatropic環電流であり，${\phi }_{-m}$がHOMOの場合のみ生じる．$j_{-m}$をビオ・サバールの式に代入して円周上で積分すると，外部磁束密度$B_0$が円電流を介して作る誘起磁束密度$B_{Induced}$を得る．   

$\begin{array}{c}{B}_{Induced}={\int }_C^{}dB={\int }_0^{2\pi r}\frac{{\mu }_0}{4\pi }\left(\frac{j_{-m}}{2\pi r}\right)\times \frac{r}{r^3}ds\\ =\frac{e^2}{m_e}\frac{{\mu }_0}{4\pi }\frac{1}{r}\left(1-\frac{m^2}{\xi }\right)\end{array}$

(1)式で示したように$B_0$と$B_{Induced}$の比が磁気遮蔽定数${\sigma }_{}^{\left(\text{III}\right)}$となる．   

${\sigma }_{}^{\left(\text{III}\right)}=\frac{B_{Induced}}{B_0}=\frac{e^2}{m_e}\frac{{\mu }_0}{4\pi }\frac{1}{r}$

×(電子数)

$-\frac{e^2}{m_e}\frac{{\mu }_0}{4\pi }\frac{1}{r}\frac{m^2}{\xi }\times 2={\sigma }_{}^{\left(\text{II}\right)}$

上式${\sigma }_{}^{\left(\text{III}\right)}$は前節で示した${\sigma }_{}^{\left(\text{II}\right)}$と完全に一致する．

円電流モデルの帰結として，常磁性項に寄与する環電流が流れる条件は，磁気量子数$-m$と$+m$の軌道が占有軌道と非占有軌道にそれぞれ分かれているときのみである．平易に云えば円周方向のnodeの数が同じ軌道が占有と非占有に分かれた場合に常磁性環電流が流れ，常磁性項が生じる．勿論，実在の分子の状況は複雑ではあるが [11]，${\phi }_{-m}$→${\phi }_{+m}$の遷移が環電流つまり常磁性項の主要な寄与であることは間違いないであろう．一方，反磁性項は電子密度が存在すれば生じる項である．

6 モデル分子H₁₂とface-to-face H₁₂- H₁₂

3∼4節のモデルIとモデルIIで計算した内容をab-initio MO計算で実演してみる．文献 [1]の3.5項(Table 7)では類似のモデル計算が$\sigma$−芳香族性/$\sigma$−反芳香族性の例として使われている．本解説では，$\sigma$−，$\pi$−芳香族性とは関係なく，円運動モデルの挙動を検証するために使う．Figure 4 (左)には12個の水素原子を半径1.4 Åの完全な円周上に等間隔に並べたH₁₂クラスターを示す．これは3節のモデルIに対応する．近接原子間距離は0.71 Åとなる．一方，Figure 4 (右)は円の縦1.2倍に拡大し，横を1.2倍に縮小した楕円の円周上に水素原子を並べた．この系では軌道エネルギーの縮退が崩れて4節のモデルIIに対応する状態となる．水素原子にはSTO-3Gのs型原子軌道を置いた．ab-initio法においても核磁気遮蔽定数${\sigma }_{\text{N}}^{}$は反磁性項と常磁性項に分けて記述することができ，本計算(非相対論的ab-initio法)では次式を用いた．   

${\sigma }_{\text{N}}={\sigma }_{\text{N}}^{\text{dia}}+{\sigma }_{\text{N}}^{\text{para}}$

  

$\begin{array}{c}{\sigma }_{\text{N}}^{\text{dia}}=\sum _k^{occ}\frac{e^2}{2m_e}\frac{{\mu }_0}{4\pi }⟨{\psi }_{0k}\left|\frac{r\cdot r_{\text{N}}1-r_{\text{N}}\otimes r}{r_{\text{N}}^3}\right|{\psi }_{0k}⟩\\ {\sigma }_{\text{N}}^{\text{para}}=-\sum _k^{occ}\frac{2e}{m_e}\frac{{\mu }_0}{4\pi }⟨{\psi }_{0k}\left|\frac{L_{\text{N}}}{r_{\text{N}}{}^3}\right|\frac{d{\psi }_{0k}\left(B_0\right)}{d{B}_0}⟩\end{array}$

Figure 4.

 Twelve hydrogen atoms on circle and ellipse. The radius of circle is $r_0=1.4$Å.

The horizontal/vertical radii of ellipse are $1.4/1.2$ and $1.4/1.2$Å respectively.

ここで$\otimes$は直積であり，$r_{\text{N}}^{}$は共鳴核Nを原点とする電子座標である．GIAO補正が加わると純粋な反磁性項と常磁性項の物理的イメージが損なわれるので，本計算ではGIAO補正は加えずに分子座標の原点とゲージ原点の両者を円の中心に置いた．

Table 1に計算結果を示す．円形H₁₂では軌道エネルギーが縮退しているので，2，6，10電子系のみが閉殻系となる．楕円形H₁₂では軌道エネルギーの縮退が崩れているので任意の偶数電子で閉殻電子系となる．

Table 1.  Components of magnetic shielding ${\sigma }_{\text{H}zz}^{}$ on the center of circle and ellipse H₁₂ clusters (ppm).^a)

Shape	Number of electrons	${\sigma }_{\text{H}zz}^{\text{dia}}$	${\sigma }_{\text{H}zz}^{\text{para}}$	${\sigma }_{\text{H}zz}^{}$
circle	2	18.9	0.0	18.9
circle	6	55.3	0.0	55.3
circle	10	91.0	0.0	91.0
ellipse	2	18.1	0.0	18.1
ellipse	4	34.9	-27.8	7.1
ellipse	6	53.9	-1.5	52.4
ellipse	8	72.6	-162.1	-83.5
ellipse	10	90.1	3.4	93.5

a) ${\sigma }_{\text{H}zz}^{}$=-NICSzz

円形H₁₂系はモデルIに，楕円形H₁₂系はモデルIIに対応している．表1のどちらの系でも，反磁性項は電子数にほぼ比例しており，1電子あたり9.0∼9.5 ppmは3∼4節の円運動モデルと妥当な一致を示す．常磁性項は，2，6，10電子系はほぼゼロとなる．これは，占有軌道→非占有軌道に磁気的許容な遷移が存在しないからである．一方，4，8電子系の常磁性項は大きな負値となる．つまり，4，8電子系では磁気的に許容な遷移，つまり${\phi }_{-1}$→${\phi }_{+1}$若しくは${\phi }_{-2}$→${\phi }_{+2}$の寄与によって常磁性環電流が流れて反遮蔽が生じる．尚，GIAO補正が加わると，表1のような単純明快な傾向が得られない．勿論GIAOを使っても誘導電流を計算することはできるが [14]，直感的理解が難しくなる．

環状のπ系化合物を2段に積んだ化合物の計算が紹介されている [15, 16]．この化合物のモデル計算を示す．上述の円形H₁₂を1.5Åだけ離してface-to-faceで2段に重ねた．結果はH₁₂-H₁₂間の距離にも依存するであろうが，本モデルはH₁₂-H₁₂間の相互作用が弱いときの典型的な結果である．表2に4電子系と6電子系の2段構造の${\sigma }_{zz}^{}$を示す．両者の常磁性項は完全にゼロとなる．Figure 5に軌道位相の概略を示す．結合性($m=\pm 1$)→反結合性($m=\pm 1$)の遷移は磁気的に全て禁制であり，このモデルでは常磁性環電流は流れない．Face-to-faceの相互作用が穏やかであれば，基本的には反芳香族性化合物も芳香族性化合物も2段重ね構造にするとNICSの基準では芳香族性化合物であると云える．この結果は文献 [14]の結果と異なる．

Table 2.  Components of magnetic shielding ${\sigma }_{zz}^{}$ on the center of the face-to face "H₁₂ − H₁₂" cluster (ppm).^a)

Shape	Number of electrons	Dia	Para	Total
circle×2	4+4=8	54.2	0.0	54.2
circle×2	6+6=12	78.6	0.0	78.6

a) ${\sigma }_{zz}^{}$=-NICSzz

Figure 5.

 Phase of low-lying molecular orbitals in the face-to-face H₁₂-H₁₂ cluster. The occupancy and energy levels of electrons are also shown together. An 8-electron system (4-electron H₁₂ + 4-electron H₁₂) is assumed in this occupancy.

7 余談

NICSの元祖であるP. von R. Schleyer教授らは，ベンゼン中央のNICS値が-10.6ppmであることを報告している [17]．その内訳は下記の通りである(文献17のTable 1を参照)．

σ電子 +2.3ppm

π電子 −9.6ppm

CH結合 −3.0ppm

core電子 −0.3ppm

このデータは円運動モデルの範囲をやや超えるが興味深いのでコメントしておく．6電子のπ電子系から反磁性的な寄与があることは議論してきた通りである．一方，$\sigma$電子が合計として常磁性的(+2.3ppm)であることは理解し難い．$\sigma$軌道には常磁性環電流が流れていると考えざるを得ない．

ベンゼンの$\sigma$電子数はcore電子とπ電子を除くと24個である(C-H結合とC-C結合の電子を分けることは困難である)．$4n$電子系だから常磁性環電流が流れるのか?，そんな単純な話ではなさそうだ．Figure 6はベンゼンの$\sigma$軌道の概略図の一部である．ベンゼンの$\sigma$軌道は「平面」の自由度をもつため，その軌道は磁気量子数$m=0,\pm 1,\pm 2,\cdot \cdot \cdot$を持つと同時に，動径量子数$n=1,2,3,\cdot \cdot \cdot$を持つ．$n=2$の軌道はベンゼンの内側と外側の±位相が異なっている(C-H結合が混在する為)．$\sigma$電子の状態をこの2つの量子数(n, m)で表現すると，(1,2)→(2,-2)，及び，(1,-2)→(2,2)は±m→∓mの遷移であるために許容となる(Figure 6中に矢印で示す)．nの変化は磁気的遷移の許容・禁制に関与しない．この励起によってベンゼンの$\sigma$軌道に常磁性環電流が流れる．

Figure 6.

 Magnetically allowed transitions between occupied and unoccupied σ-orbitals, which are shown by orange-colored arrows. ($n,m$) means the principle quantum number and magnetic quantum number respectively.

8 まとめ

円運動モデル円形水素原子モデルと核磁気遮蔽定数(-NICS)の関係についてのポイントを纏める．

(1)反磁性項は基底状態の電子密度だけに依存し，常磁性項は磁場応答から生じる．前者は遮蔽，後者は反遮蔽に寄与する．

(2) (4n+2)電子系の場合は反磁性項のみが生じる．(4n)系の場合は反磁性項と常磁性項の両方が生じて相殺が起こる．常磁性項はHOMO-LUMOギャップに反比例する．

(3)量子力学的な確率密度流に対応する環電流から反磁性電流と常磁性電流を作ることができ，それらの電流から生じる核磁気遮蔽定数(-NICS)はRamseyの式から得た結果と一致する．

(4) ab-initio計算によるH₁₂クラスターの結果は1次元円運動モデルと半定量的に一致した．また，円形の水素原子モデルの範囲で，反芳香族性をface-to-faceで2段に重ねても，NICS的な指標では，芳香族性は生じないことが示された．

本モデルの結果を実在系に当てはめると，(4n+2)π電子系化合物ではそもそも環付近の電子密度が高く，それゆえに反磁性項の値が大きく，NICSは負値となるのであろう．一方，(4n)π電子系化合物では顕著な常磁性項が発生し(つまりparatropic環電流が発生し)，NICSは正値にシフトする．本解説記事がNICSを扱って芳香族性・反芳香族性を議論する研究者の皆様の一助となれば幸いである．

謝辞

東京都立大学理学部化学科の西長亨准教授にご貴重な御助言を頂いたことに感謝申し上げる．

参考文献

• [1]   Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta, and P. von R. Schleyer, Rhys. Rev., 105, 3842–3888 (2005).
• [2]   C. Corminboeuf, T. Heine, J. Weber, Phys. Chem. Chem. Phys., 5, 246 (2003). doi:10.1039/b209674a
• [3]   T. Heine, J. Phys. Chem. A, 107, 6470 (2003). doi:10.1021/jp035163z
• [4]   a)Y. Ruiz-Morales, J. Phys. Chem. A, 108, 10873 (2004). b) M. Mauksch, V. Gogonea, H. Jiao, Angew. Chem. Int. Ed., 37, 2395 (1998).
• [5]   P. Lazzeretti, Phys. Chem. Chem. Phys., 6, 217 (2004). doi:10.1039/B311178D
• [6]   F. Sondheimer, Acc. Chem. Res., 5, 81 (1972). doi:10.1021/ar50051a001
• [7]   a) R. Ditchfield, Mol. Phys., 27, 789 (1974). b) K. Wolinski, J. F. Hinton, P. Pulay, J. Am. Chem. Soc., 112, 8251 (1990). c) J. R. Cheeseman, G. W. Trucks, T. A. Keith, M. J. Frisch, J. Chem. Phys., 104, 5497 (1996).
• [8]   J. A. Pople, Proc. R. Soc. Lond. A Math. Phys. Sci., 239, 577 (1957).
• [9]   N. F. Ramsey, Phys. Rev., 78, 699 (1950). doi:10.1103/PhysRev.78.699
• [10]   E. N. Lassettre, A. Skerbele, M. A. Dillon, K. J. Ross, J. Chem. Phys., 48, 5066 (1968). doi:10.1063/1.1668178
• [11]   G. Merino, T. Heine, G. Seifert, Chemistry, 10, 4367 (2004). doi:10.1002/chem.200400457 PMID:15352120
• [12]Ryoshi Kagaku Nyumon(Ge), Chapter 12, T. Yonezawa, T. Nagata, H. Kato, A. Imamura, K. Morokuma, The 3rd Edition, Kagaku Doujin
• [13]   J.Larmor D. Sc F. R. S., Philos. Mag. Ser. 5, 44, 503 (1897).
• [14]   J. Jusélius, D. Sundholm, J. Gauss, J. Chem. Phys., 121, 3952 (2004). doi:10.1063/1.1773136 PMID:15332941
• [15]   D. E. Dean, P. W. Fowler, Org. Lett., 10, 5573 (2008). doi:10.1021/ol802417n PMID:19007173
• [16]   C. Corminboeuf, P. von Ragué Schleyer, P. Warner, Org. Lett., 9, 3263 (2007). doi:10.1021/ol071183y PMID:17658752
• [17]   P. R. Schleyer, M. Manoharan, Z. X. Wang, B. Kiran, H. Jiao, R. Puchta, N. J. R. van Eikema Hommes, Org. Lett., 3, 2465 (2001). doi:10.1021/ol016217v PMID:29446959