2014 Volume 31 Pages 181-199
2014 Volume 31 Pages 181-199
In general a force will act on a particle illuminated by light or other radiation and absorbing part of the flux, and as a consequence a motion will result. It is caused by the interaction of gas molecules with the particle’s surface, which is hotter than the surroundings. This surface must be inhomogeneous with respect to accommodation and/or temperature. Gas molecules, impacting and reflected from the particle’s surface with accommodation, transfer some momentum from the particle and thus cause the force. For a temperature variation on the particle’s surface, the force points from the hot to the cold part, thus in the direction of the incident radiation, and under very special conditions it can be the opposite. A particle’s surface having a variation in accommodation coefficient will cause a force from the locations of higher to lower accommodation. Usually this will cause both a linear force and a torque. The latter in combination with Brownian rotation will result in a zero net force. But it is possible that an external torque acting on the particles causes an orientation. The torque can be caused by magnetic or electric fields on magnetic or electric dipoles in the particles or by gravity orienting inhomogeneous particles. For micrometer- and nanometer-sized particles, the photophoretic force can exceed gravity. Photophoresis is important for levitation in the stratosphere and for planet formation, it can also be used for on-line particle separation, or in clean-room technology or in geo-engineering.
Particles illuminated by a beam of light or infrared radiation, having sufficient flux density, can move in various directions. This phenomenon has been mentioned by Thoré (1877), first described and later intensively studied by Ehrenhaft (1918) and co-workers/students. Since light is the cause for the motion, the expression “photophoresis” has become common. Preining (1966) gives a concise description of the important factors influencing photophoretic motion: “This motion can depend on the illumination, color, structure and shape of the light beam, on pressure and composition of the gas, on the particle’s size, shape and material, and on additional fields such as electric, magnetic, and so on.”
The motion of the particles can range between simple to very complex, and depends both on the particle and the external forces (see Fig. 1). The simplest motion is (a) positive photophoresis, in which case the particles move in the direction of the light beam; motion in the opposite direction is possible, this is called (b) negative photophoresis. For particles having the right surface and volume properties, a motion in or against the direction of an external field is possible, this is called (c) gravito-, electro-, or magneto-photophoresis, depending on the field. Illuminated particles may perform an irregular motion, similar to an enhanced Brownian motion, called (d) irregular photophoresis. In the case of inhomogeneous illumination and/or inhomogeneous fields, the particles may undergo (e) circular photophoresis, having circular or elliptical orbits, or (f) complex photophoresis, which can be a combination of several motions. Finally no photophoresis can occur, i.e. the illumination by light causes no motion in addition to the motion without light.

Types of photophoresis. When illuminated, particles can move in or opposite to the direction of light (a, b), move in the direction of external fields (c), move similar to Brownian motion but more vigorously (d), move in closed loops (e) or perform complex motions.
The photophoretic force can be larger than gravity for particle sizes comparable to the mean free path of the gas molecules and thus can cause a motion against gravity, leading to the formation of aerosol layers in the stratosphere, photophoresis also plays an important role in planet formation. For geo-engineering, the photophoretic force can help to keep particles suspended longer. In intense laser light, absorbing and non-absorbing particles can be separated on-line, the microchip production zone can be kept particle-free, and single particles can be handled by a photophoretic trap. Photophoresis will slow coagulation. Whenever strong light flux and microparticles occur simultaneously, photophoresis cannot be neglected, such as during combustion of fuel droplets.
The momentum transferred by photons hitting a surface and absorbed or deflected obviously exerts a force on a particle in the direction of the photon motion. Using the classic electromagnetism interpretation of radiation pressure, it amounts to
| (1) |
The force exerted by incident light can easily be demonstrated with a radiometer. It consists of a rotor with vanes (made of aluminum or mica which are dark on one side, and reflecting on the other) in a partial vacuum. When exposed to radiation the light mill turns (for a motion picture see, e.g. http://en.wikipedia.org/wiki/File:Radiometer_9965_Nevit.gif). A schematic of the radiometer can be seen in Fig. 2. The reflected photons cause a higher momentum than the absorbed ones, thus the rotor should turn counterclockwise. In reality the opposite is the case. Applying formula (1) the motion should be very slow (see, e.g. the problem 59 in chapter 29 of Tipler, 1991); it would need several years until a few revolutions per second are reached, in reality the wheel immediately turns after switching on the light. Except for extremely intense radiation, this direct photophoresis (radiation pressure) is of minor importance for the radiometer and also for aerosol science, and thus can be neglected. The indirect photophoretic force, as treated below, is much stronger, but needs the presence of gas molecules which are available in the radiometer and are always present in an aerosol.

Schematics of the radiometer wheel.
On a microscopic scale, gas molecules impacting on the surface are reflected. The reflection can be specular (approximately 10% of the molecules) or diffuse (90%, Fuchs 1964, p. 22), obviously with conservation of energy. The diffuse reflection is accompanied by a more or less complete accommodation (see below). For a particle moving through a gas, the molecules impacting at the front side are reflected with a higher velocity compared to the backside. This asymmetry in velocities leads to a momentum transfer to the particle and causes the friction force acting on the particles when moving through a gas.
The reflection of gas molecules at the particle’s surface with accommodation
is of special importance for photophoresis. A surface of a particle which absorbs
radiation (visible of IR) is heated to a higher temperature
Ts than the temperature T0
of the surrounding gas. A gas molecule hitting the particle’s surface can
acquire some of the thermal energy of the hot particle and be
“reflected” with a velocity corresponding to a temperature,
T, that is higher than the surrounding gas. The probability of
taking up additional thermal energy is characterized by the accommodation
coefficient
| (2) |
If the accommodation coefficient α of the surface of the particles is α > 0 and the particle is heated by radiation, a photophoretic force can act on the particle. Two different idealized extremes can be distinguished: (a) Variation in temperature on the surface of the particles (ΔT force) and (b) variation of accommodation and constant temperature (Δα force):
Case (a): Constant accommodation coefficient but variation in surface temperature (ΔT-photophoretic force)Let us assume a spherical particle of diameter d consisting of a light-absorbing material with a thermal conductivity kp and immersed in a gas with pressure p, viscosity η, and molecular weight M and illuminated by visible or infrared light. The surface facing the radiation source is warmer than the backside (see Fig. 3); due to accommodation, the molecules on the warmer side leave the surface faster, resulting in a force away from the light source (positive photophoresis). This was found to take place, e.g. for particles consisting of Au, Ag, Hg, Cd, K, Na, Mg, soot produced by the combustion of turpentine, or camphor (Ehrenhaft, 1918).

Explanation of positive and negative photophoresis (Rubinowitz, 1920). The surface of a strongly absorbing particle is hotter on the side facing the radiation, thus photophoresis is in the direction of the radiation. A particle that slightly absorbs light focuses the light to the rear side, which consequently is hotter, thus the particle moves in the opposite direction.
For a slightly absorbing particle, a force in the opposite direction has been observed. The maximum absorption may be at the backside, causing the reversal of the force. The early interpretation is the lens effect, see Fig. 3: The convex surface of the particle acts like a lens, concentrating the rays on the backside (Rubinowitz, 1920), which becomes hotter than the surface facing the radiation, resulting in a motion towards the light source (negative photophoresis). For particles comparable to the wavelength of light, the lens effect as a simplification may not be permitted, but strictly applying Maxwell’s equation to an absorbing spherical particle leads to the same results (Dusel et al., 1979; Figure 4.31 of Barber and Hill, 1990). Negative photophoresis has been observed, e.g. for spheres of S, Se, J, Bi, Th, P, Pb, Te, As, Sb, for tobacco or wood smoke particles (Ehrenhaft, 1918).
The direction of the photophoretic force is determined by the direction of the radiation and is almost independent of the orientation of the particle, thus the force is called space-fixed, the movement is called longitudinal photophoresis and since the temperature difference causes the force, it is called ΔT force. Although all particles perform Brownian rotation, the rotation is slow compared to the time needed to establish the temperature gradient within the particle (Fuchs, 1964, p. 62). The “ideal” particles would have a low thermal conductivity and heat capacity.
In the free molecular regime, calculation of the force is simple: Molecules impacting on the particle are reflected with a larger velocity due to accommodation. Using considerations similar to the radiometer which was considered above, Rubinowitz (1920) determined the force on a spherical particle with diameter d at gas pressure p as:
| (3) |
For the derivation in the continuum regime one has to consider the thermal creep flow around the particle and the resulting viscous forces. In contrast to the free molecular regime, the gas molecules around the particle have temperatures similar to those on the surface of the particle (see Fig. 4). A gas molecule impacting on the surface from the left (hot) side thus has a larger velocity than the molecule impacting from the colder side. After accommodation, the molecules have a symmetric velocity distribution with respect to the perpendicular direction of the surface, therefore the warmer molecule coming from the left side transfers to the particle a larger momentum to the right than the colder molecule to the left. This results in a net force on the particle which directs from the hot to the cold side. The gas loses this momentum, thus a creep flow around the particle from the cold side to the hot side occurs simultaneously which has its maximum flow at a distance to the mean free path of the gas (Knudsen, 1910a, b; Hettner, 1924; Fuchs, 1964, p.57). Solving the hydrodynamic equations (similar to Stokes Law), the following formula for the photophoretic force is obtained (Hettner, 1926)
| (4) |
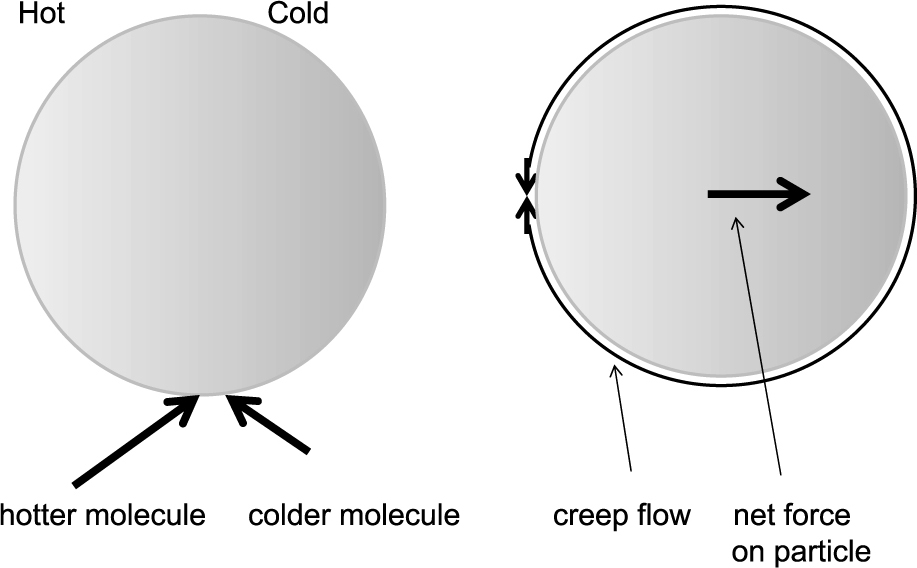
Photophoretic force on a particle in the continuum regime. The particle is hotter on the left side and in the immediate vicinity of the surface, the gas molecules have the same temperature as the surface. Molecules impacting on the particle from the left are faster than those coming from the right, transferring a momentum to the right onto the particle. This momentum is lost in the gas, thus a thermal creep flow of the gas molecules to the left occurs.
Formula (3) is valid for the free
molecular range, i.e. the particles must be considerably smaller than the mean
free path of the gas molecules (λ = 66 nm at
standard conditions, with decreasing pressure the mean free path increases),
whereas formula (4) is only valid
for the continuum range, i.e. for particles much larger than
λ. Magnitudes influencing the force are the diameter of
the particle and the temperature gradient both proportional to the force in
formulas (3) and (4), the accommodation coefficient only
in (4) and the pressure in (3) and (4). The force is proportional to the pressure in the free
molecular regime (3) and
inversely proportional to it in the continuum regime (4), i.e. a maximum force occurs in
between, which is the most important range for photophoresis. Similar to
Stokes’ Law, an interpolation is used for the intermediate range, as
proposed by Hettner (1926):
| (5) |
The pressure-dependent force for a given particle size has a maximum for p = p0, or for a given pressure the maximum photophoretic force is for particle diameter d0. The pressure for the maximum photophoretic force depends on the gas properties, the particle size and the accommodation coefficient. For a pressure of 1 bar the optimum particle size is 229 nm for α = 0.8 and 375 nm for α = 0.3. For a pressure of 5500 Pa (20 km a.s.l.), the corresponding diameters are 6.8 and 4.1 μm.
The viscosity of the gas, η, is obviously decisive for
the photophoretic force in (4).
The viscosity of a gas is mainly determined by the mean free path,
λ, of the gas molecules and the pressure. Using the
relation
Denoting the maximum force at p0 with F0, (5) can be written as
| (6) |
This formula has been tested by many authors. Various particle materials, particle sizes, gases and pressures have been used. Usually the accommodation coefficient and the particle size are not known exactly, whereas the temperature gradient is completely unknown. The experimental procedure is quite elaborate, since the motion of one and the same particle is measured for pressures varying over three orders of magnitudes, lifting the particle up in between. Formula (6) contains only magnitudes that are experimentally accessible. Since the size of the particle in relation to the mean free path of the surrounding gas is important, it is also possible to make photophoretic analogy experiments with centimeter-sized particles, as long as the mean free path of the particles is large enough. This requires a high vacuum but offers the advantage that the particle can be fixed, and the force can be measured with a torsion balance. In this way many data points can be gathered, without the fear of losing the particle during pressure change (Schmitt, 1961). Compared to the experiments with sub-micrometer-sized particles, the distance to the walls of the container is much smaller, and wall effects cannot be neglected. A summary of various experiments is shown in Fig. 5. Particles consisting of Te, Se (Mattauch, 1928), Se (Reiss, 1935), CdS (Arnold et al., 1980) and also 1-cm polystyrene particles at correspondingly low pressures (Schmitt, 1961), all show the same behavior for gases such as H2, A, O2, N2, CO2. All data demonstrate the maximum photophoretic force at an intermediate pressure.
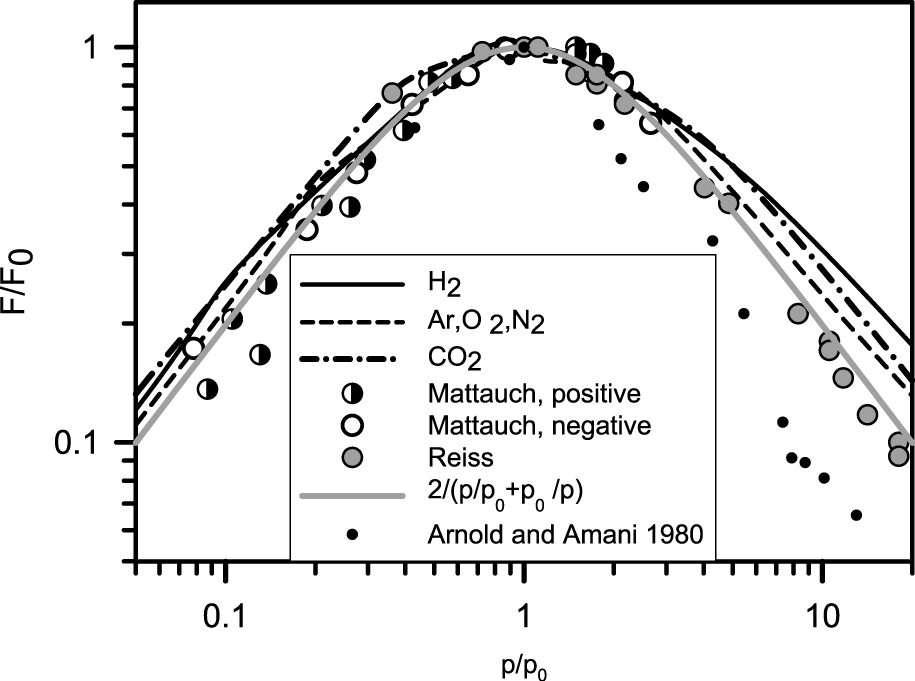
Experimentally determined photophoretic forces as a function of pressure. All data show a maximum photophoretic force at an intermediate pressure as postulated by theory. The dark lines are results of model measurements with cm-sized spheres in vacuum, the points result from measurements made with individual micro-or nanometer-sized particles consisting of various materials, the gray line is theory (6).
Once the size and the photophoretic force of the particle is known, equation (4) can be used to estimate the temperature difference between the hot and cold side of the particle. Ehrenhaft (1918) and Parankiewicz (1918) have measured the photophoretic forces: They are in the order of 10−16 to 10–15 N for particle radii ≤ 100 nm of various materials in N2 and Ar. The estimate for the temperature difference across the particles is 10−4 to 10−2 K (Hettner, 1926).
For calculation of the photophoretic force in (3) and (4), the
temperature gradient in the particle is needed. For this, both the inhomogeneous
heat production within the particle, the heat conduction to the surface, and the
momentum transfer at the surface has to be solved. Fuchs (1964, p. 58) remarks: “The
main difficulty in calculating the radiometric force on a particle is the
determination of the temperature gradient in the particle
itself.” For simple shapes such as spheres this appears
possible (see below), but many particles showing photophoresis are not spheres.
A first attempt for spheres has been made by Rubinowitz (1920) yielding
Using all available theories, Rohatschek (1995) formulated an empirical model. For the free molecular and the continuum regime, the force on a particle with diameter d illuminated by a flux density S is obtained as
| (7) |
| (7a) |
With kp the thermal conductivity of the particle,
J1 the asymmetry parameter for light absorption
(½ for opaque particles, J1 has the opposite
sign if absorption is mainly at the backside, e.g. for negative photophoresis),
D a factor only containing the gas properties, thus independent of particle size
and pressure, κ the thermal creep coefficient
(κ = 1.14 for a fraction of 0.1 of the
specular-reflected molecules, Bakanov,
1992), and p* a reference pressure. (The
pressure for the maximum force is obtained by

Photophoretic ΔT force as a function of pressure for various particle diameters. The force is given relative to the weight of the particle. The data points in the right graph are for sulfur spheres (Parankiewicz, 1918)
As a simple model we assume a spherical particle of diameter d consisting of a light-absorbing material immersed in a gas with pressure p, and temperature T (mean molecular velocity c̄). The particle’s surface shall have a variation in the accommodation coefficient, e.g. be caused by a difference in surface roughness or by different materials forming the particle. For this simple model, one half of the sphere’s surface shall have the accommodation coefficient α1, the other α2 (see Fig. 7). At the location of larger accommodation coefficients, the molecules are reflected with a higher average velocity, resulting in a thrust on the particle from the location of the higher accommodation coefficient to the location of the lower one. This can be considered similar to the jet of an airplane: this thrust has a fixed direction relative to the airplane, approximately in the plane of symmetry of the airplane; if the airplane changes direction the thrust vector changes as well. Likewise the direction of the force on the particle is determined by the orientation of the particle and is independent of the direction of the illumination (the direction of the force is thus given in a body axis system, we call it body-fixed or particle-fixed force). Upon a change of orientation of the particle, the direction of the force likewise changes. Since all particles perform Brownian rotation, the direction of the force is distributed randomly, and the motion of the particles can be considered as a strongly enhanced Brownian motion (see Fig. 1d). This has been observed by various authors, e.g. Ehrenhaft (1907) and Steipe (1952), and was named the “trembling effect”. It only occurred if no orienting field was present, therefore, e.g. for iron particles, the earth magnetic field had to be compensated completely. Obviously the average (net) force is zero, due to Brownian rotation.

Photophoretic Δα force. A particle, hotter than the surrounding air, has a larger accommodation coefficient on the lower hemisphere. Consequently the molecules reflected by the lower hemisphere are faster than the ones on the upper hemisphere, resulting in an upward-directed thrust.
The instantaneous Δα-photophoretic force on the particle in the direction from higher to lower accommodation coefficients amounts to (Rohatschek, 1995)
| (8) |
As an example, the photophoretic Δα force (formula (8)) for particles having Δα = 0.1 and α = 0.7, consisting of an absorbing material with a refractive index m = 1.6 – 0.66 i and a density of 2000 kgm−3, illuminated by 1000 Wm−2 at 550 nm at a temperature of 293 K, is shown in Fig. 8 (left). For better comparison, the force is given as a ratio to the weight of the particle. Similar to the ΔT force, it decreases with increasing pressure, but there is no decrease for low pressures. The force is considerable, for particles of 0.2 μm it is more than 10 times the weight, causing, e.g. the trembling motion as observed, e.g. by Steipe (1952).

Photophoretic Δα force as a function of pressure for various particle sizes. The force is given relative to the weight of the particle. Left side: Force on a particle, which is assumed to be fixed in space. Right side: average force for a particle oriented by a magnetic field, but disturbed by Brownian rotation.
But this force continuously changes direction due to the Brownian rotation of the
particle. The mean square angle of rotation
| Diameter [μm] | 0.1 | 0.2 | 0.5 | 1 | 2 |
|---|---|---|---|---|---|
| Average revolutions in 1 second
|
61. | 21 | 5.44 | 1.92 | 0.68 |
Considering the vigorous rotation, it is immediately evident that none of the above particles will perform a reasonably straight motion.
The situation changes immediately if the particle orientation is forced in a
certain direction. For our considerations we will assume the particle is located
in a magnetic field B and has some remanent magnetism characterized
by the magnetic momentum m (Fig. 9). The particle orients itself such that its
magnetic momentum points in the direction of the magnetic field. The direction
of the photophoretic force does not usually coincide with the direction of the
magnetic moment and the angle between the two is δ. The
particle can still freely rotate around the axis of the magnetic moment,
therefore all force vectors are located on a cone with an opening angle of
2·δ. But Brownian rotation is stochastic, thus
the photophoretic force will cause a quasi-helical motion (see insert of Fig. 9). The averaged force on the
direction of the field is obtained by multiplying the instantaneous force (8) with cos
δ. Brownian rotation is not only around the axis of the
magnetic momentum, but it will also disturb the orientation of the force vector,
which we have so far assumed to be at angle δ to the magnetic field
line. The stronger the magnet, the less deviations from this direction will be
possible. The competition between orienting torque by the magnetic field and the
disorientation by thermal disturbance is very similar to the orientation of
magnetic dipoles in the theory of paramagnetism (see, e.g. Brand and Dahmen, 2005, pp. 290–294): The
magnetic dipole with magnetic moment m in the magnetic field
B has a potential energy, m·B,
its thermal energy is kT. The ratio

Particle containing a magnetic dipole in a magnetic field. The particle is oriented such that the magnetic dipole moment points in the direction of the magnetic field. Rotation around the axis is possible, and the photophoretic force vectors are positioned on a cone with an opening angle of 2δ (right). Due to the stochastic manner of Brownian rotation, the particle performs a quasi-helical motion (left).
Using the formalism of paramagnetism, the projected force is multiplied with the Langevin function L(x), i.e. the average projected force in the direction of the magnetic field using (8) is
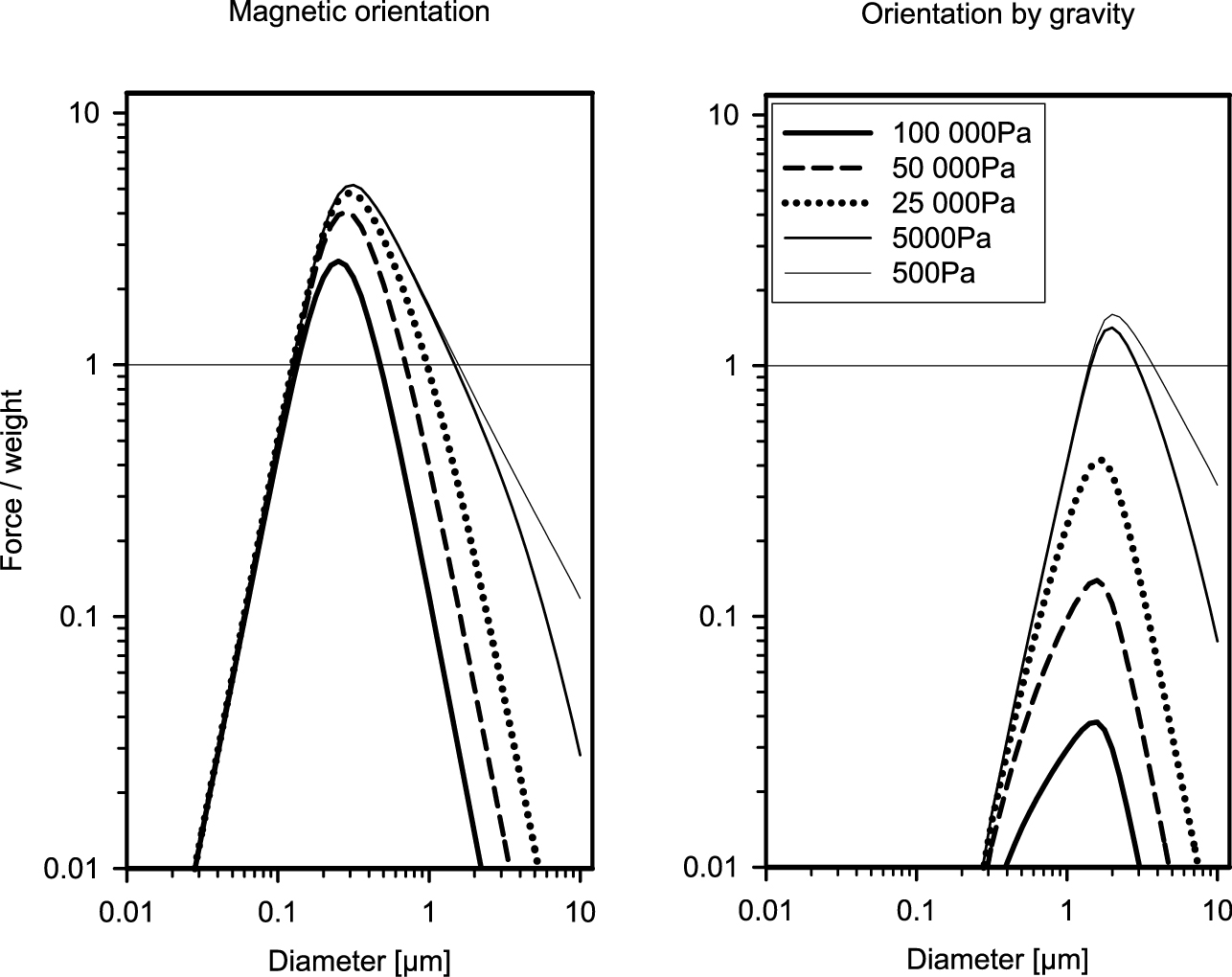
Relative photophoretic Δα force: Left: Magnetic orientation of the particle. Right: Orientation by gravity. For conditions above the horizontal line, levitation in the atmosphere is possible.
The Δα force can be channeled around one direction if an orienting torque exists. This has been shown above for magnetic orientation, but is also possible by electric fields or by gravity. A typical everyday example of orienting torque by gravity would be a fishing float which usually stands upright in the water, when disturbed it will return to its initial position due to the uneven distribution of mass. An inhomogeneous distribution of mass will orient the particle in the same way. This can be seen in Fig. 11: Assume a particle having different accommodation coefficients on the two hemispheres causing a photophoretic force to upwards right. (a) The center of gravity is displaced from the center of the photophoretic force by a vector q. Gravity and photophoretic force vectors jointly cause a motion of the particle to the right and slightly upwards; (b) the motion of the particle causes a friction force which is added to the photophoretic force. Now gravity and the other forces are balanced and a stationary state is reached; but, due to the offset of the center of gravity and the center of photophoretic plus friction force, a torque acts on the particle, rotating it counterclockwise until the center of photophoretic force is above the center of gravity. This results in an upward motion, since the photophoretic force is larger than the weight (c).

Orientation of a particle by gravity: (a) The center of mass of the particles is displaced by a vector q. The photophoretic force (due to different accommodation coefficients) added to the weight of the particles causes a motion to the right. (b) The friction is a vector to the left (b), adding friction and photophoretic force yields a vertical vector. Since the two vertical vectors are anchored at different points, a torque on the particle forces it to rotate (c) until the two anchor points are above each other (c).
The orientation of the particle is disturbed by Brownian rotation, the important
magnitude is the ratio of the potential energy Ep
=
m·g·q to the
thermal energy Eth =
k·T, i.e. the value given by eq. (8) has to be multiplied by
L(x) with
The Δα-photophoresis needs an orienting field, thus it is called field photophoresis, specifically gravito-, magneto-or electro-photophoresis. For optimum Δα-photophoresis, the particles should have a considerable variation of the accommodation coefficient on the surface and a high thermal conductivity, in order to have a homogeneous temperature on the surface.
(c) Other types of photophoresisIn the two previous sections we have assumed the particle to be spherical and having a rather symmetric distribution of the accommodation coefficients on the surface. It is hard to imagine that particles formed by combustion, coagulation, condensation on existing surfaces, mechanical abrasion or interstellar dust particles fulfill these requirements. It can be assumed that particles illuminated by light have a temperature gradient on their surface (needed in ΔT force), but it is unrealistic for a particle to have the same temperature everywhere on an inhomogeneous surface, as we assumed for the Δα force. Thus Δα and ΔT photophoresis will most likely occur simultaneously.
An inhomogeneous surface of the particles will also cause a photophoretic torque. The radiometer itself (Fig. 2) is an example. Two arrangements where a photophoretic torque will act are shown in Fig. 12. The shape (a) is the “Spitzenradiometer” (pointed radiometer) theoretically investigated by Hettner (1924). The pointed ends of the body will release more thermal energy, thus be colder. The photophoretic force is in the direction of the temperature gradient, resulting in a counterclockwise torque. The particle (b) with an inclusion on the surface having a different accommodation coefficient will have a clockwise torque, if the accommodation coefficient of the surface of the inclusion is smaller than for the remaining surface. Simultaneously, an upwards Δα force acts on this particle.

Examples for particle shapes which cause photophoretic torque. (a) The “Spitzenradiometer” (Hettner, 1924). The points dissipate more thermal energy and are thus colder. Due to the temperature difference, a counterclockwise torque arises. (b) A particle with an impurity on the surface having a different accommodation coefficient. Both a torque and a Δα force arise.
In addition to the torque and the Δα-force, this particle with the inclusions (Fig. 12b) will also have a ΔT force. In the stationary state, the orientation of the photophoretic torque will be parallel to the direction of light, resulting in a helical motion around the direction of the illumination. The direction of the photophoretic Δα force need not agree with the direction of the photophoretic torque (both vectors are particle-fixed). Depending on their angle to each other, the resulting motion can be in the direction of the light or opposite (for theoretical details, see Preining, 1966, p. 130, for observations, see Lustig and Söllner, 1932).
For the Δα force, an inhomogeneous distribution of the accommodation coefficient on the surface is needed. In reality this will not be two homogeneous hemispheres, as assumed above, but a particle with a complicated surface structure. Therefore in addition to the Δα force, a photophoretic torque will make the particle rotate around a particle-fixed axis. This rotation has to be added to the linear motion caused by the Δα force. Therefore the simple picture of Fig. 9 has to be replaced by a helical movement around the field line with a constant pitch, obviously with Brownian disturbances superimposed. The average velocity or the force in the direction of the magnetic field is not altered. The same is true for gravito-photophoresis.
In an inhomogeneous horizontal illumination, oscillations along a vertical axis are possible. Consider a particle performing gravito-photophoresis with an additional photophoretic torque. The particle will have a helical movement upwards and out of the horizontal beam of light. With lower illumination, both the gravito-photophoretic force and the torque decrease and after some time for temperature adjustment, the particle follows a helical downward movement with a different pitch and then resumes the upward motion, see Fig. 1f.
In two inhomogeneous light beams in the opposite direction, complicated closed loops in the horizontal direction are possible, in rotating magnetic fields the particles have even more impressive orbits, for details see Preining (1966).
The theories above have postulated a spherical particle with some inhomogeneities with respect to accommodation coefficient or density. Experimental evidence shows that non-spherical particles are better suited for photophoresis than spherical particles. For a full theory similar to a sphere, the following problems have to be solved: Heat sources in the particle, thermal conduction in the particle to obtain the temperature distribution on the surface, and information on the accommodation coefficients on the surface. This is already difficult for spherical particles; but for simple particle shapes and structures, solutions do exist: Spheroids (Ou and Keh, 2005), cylinders (Keh et al., 2001), convex particles with rotational symmetry (Zulehner and Rohatschek, 1990), and fractal structures, using the Berry-Percival method for light interaction and a Monte-Carlo method for molecular transfer to obtain ΔT and Δα forces (Cheremisin and Vasilyev, 2004). The Monte-Carlo method offers the advantage that for whatever shape and composition of the particle, a solution is possible with the constraint of sufficient supercomputer time and detailed information on the properties of the particle, which is not usually available. Nevertheless, the findings for the simple assumption of spherical particles agree quite well with experimental results for non-spherical particles.
The following components for a successful measurement of photophoresis are needed: measuring chamber, radiation source, observation device, particle generator, pressure gauge as already described above. Since mono-disperse particles could not be produced in the early days, it was important to make as many measurements as possible with one particle. Electrostatic fields are used to bring the (charged) particles back to the initial state, being a very tedious job, especially if the pressure in the chamber was changed. So it required a lot of skill and patience to produce series of measurements which lead to the data points, e.g. shown in Figs. 5 and 6.
Ehrenhaft (1918) designed an observation cell and illumination system of maximum flexibility, a schematic can be seen in Fig. 13. The cell can be illuminated by the light of a carbon arc lamp, the infrared is filtered by a liquid filter, thus the illumination is polychromatic with wavelengths between 400 and 1200 nm. The light is concentrated by several lenses into the center of the observation cell. The flux density in the center can be up to 4000 times the solar constant. With a shutter, the illumination can be chosen to be from the right or the left side, or both. Particles in the cell are observed by a microscope, viewing perpendicular to the direction of illumination. The intense dark field illumination permits the recognition of particles down to less than 100 nm in diameter. The observation cell is made of the electrically isolating material ebonite, contains two metal plates forming a capacitor and has two glass windows for illumination and one to permit observation. Operation at low pressure is also possible. Particles are generated in various carrier gases, by processes such as electrical arc between various metal electrodes, evaporation in test tubes, or simply by using smoke, e.g. from the combustion of paper or cigarettes. The particles are charged by diffusion charging with ions produced by ionizing radiation.
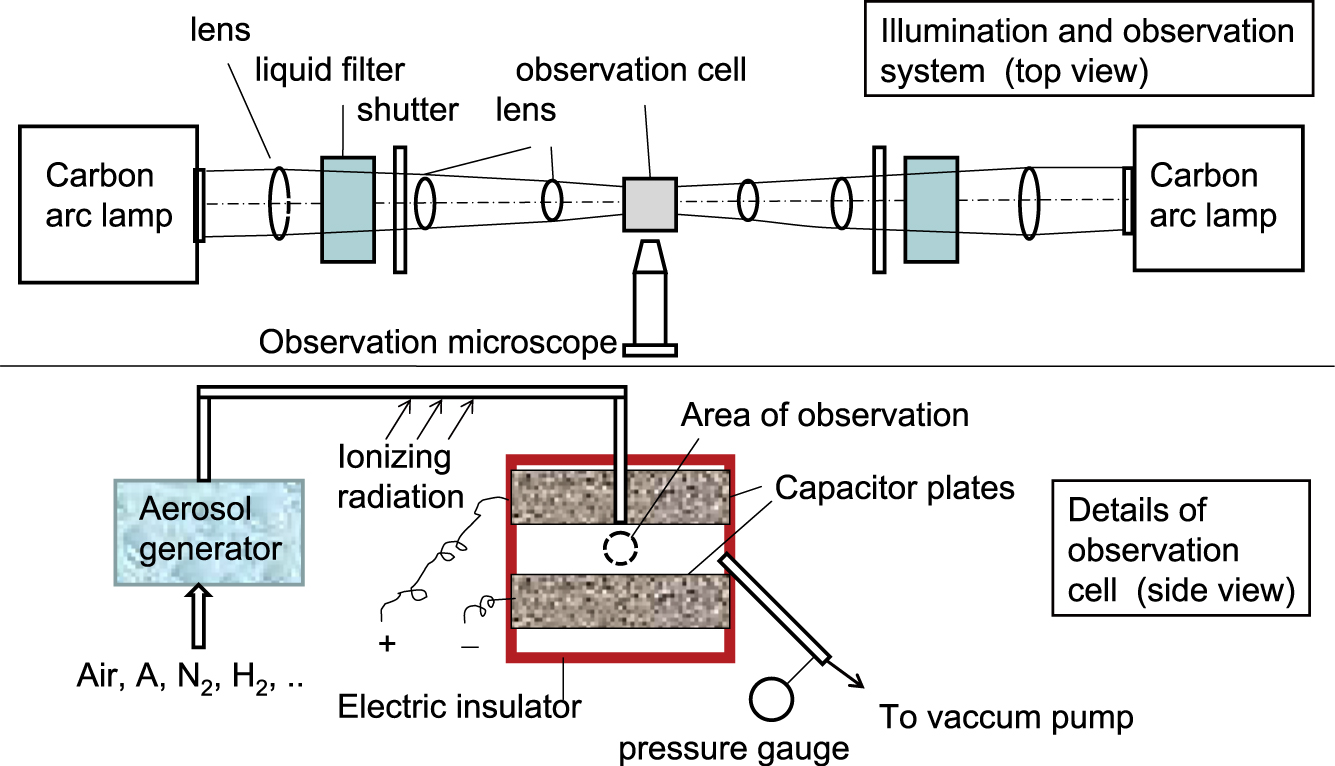
Apparatus used by Ehrenhaft (1918) for the observation of photophoresis. Top: Light is concentrated by several lenses in the center of the observation cell. The observation is done through a microscope, perpendicular to the direction of illumination. The dark field illumination permits the observation of particles sizing down to tens of nanometers. The cell can be evacuated or pressurized and is made of an electrically insulating material. Bottom: Two metal plates serve as a capacitor to exert vertical forces on charged particles. The charging of the particles is done by ionizing radiation.
To measure the photophoretic force, the particles are illuminated by light and the
velocity of the horizontal motion is measured by stopping the time needed for a
distance of 0.3 mm. Within this distance the light could be considered
homogeneously. When the particle is close to the end of the field of view, the
opposite illumination is used, bringing the particles back. When settling too far, a
voltage is applied to the plates of the capacitor, lifting the charged particles up.
In this way a series of measurements is possible with one and the same particle.
When the particle is outside of the intense beam, the photophoretic force is
negligible and the settling velocity and the velocity in the electric field can be
measured. The diameter of the particle was measured by determining the settling
velocity v and applying Stokes’ Law:
An impressive experiment demonstrating light absorption to be the reason for photophoresis has been performed by Déguillon (1950): A droplet of a dye solution is illuminated by a white light beam and shows positive photophoresis. The dye has a strong light absorption in a narrow band of wavelengths. If this wavelength range is filtered out of the beam by a slab of the same dye solution, the particle is still strongly illuminated, but shows no photophoresis.
The laser, CCD cameras and methods to produce monodisperse particles made observations simpler by far: An arrangement is shown in Fig. 14 (Haisch et al., 2008). The aerosol passes through a cell about 10 mm × 10 mm × 80 mm in size, having windows on all planes of the cuboid. The aerosol is illuminated by a green laser passing vertically through the cell. The excitation laser passes from the right to the left, the observation of the particles’ path is performed with a CCD from the front (perpendicular to the drawing plane). The particles move vertically in the cell until passing through the excitation laser beam, which deflects particles with positive longitudinal photophoresis to the right. A schematic of the CCD picture is seen on the right side. Knowing the vertical velocity vv of the particle, the photophoretic velocity vphot can be obtained by the angle ϕ between the vertical and the direction in the laser beam by vphot = vv · tan ϕ. Monodisperse polystyrene latex spheres with no absorption for green light were used, so the observation laser does not cause photophoresis. With this set-up the dependence of the photophoretic velocity on the laser flux density and the particle size have been checked and agreement with theory has been found. The photophoretic velocity depends on the material of the particles; for substances such as CuSO4, NaCl, Cu(CH3COO)2, Ni(NO3)2, KMnO4, and others, and a size of 200 nm ± 50 nm, values between −0.48 and +0.03 mm/s have been found (Kykal, 2010, p. 100).
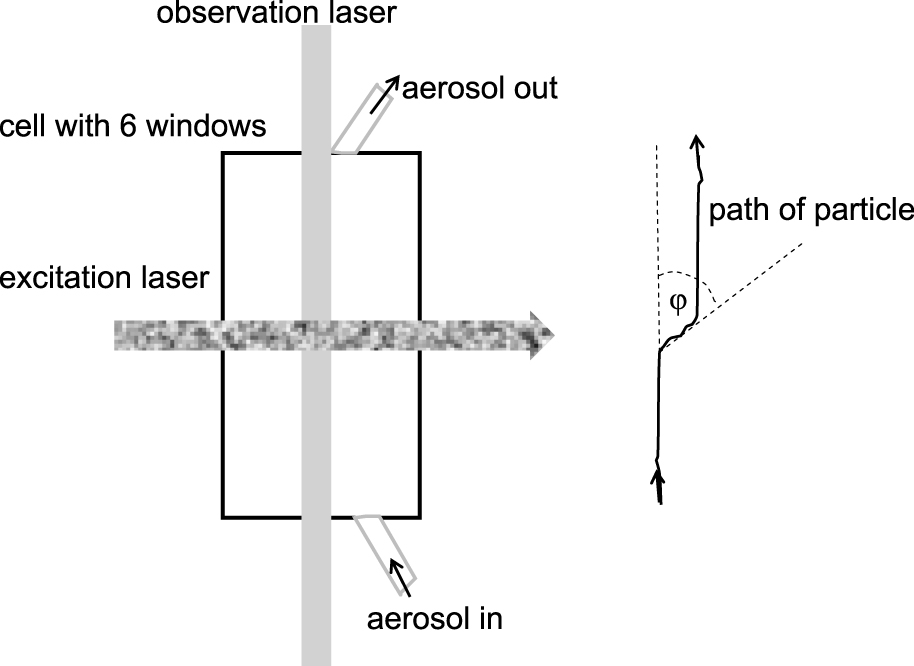
Experimental determination of the photophoretic velocity: A continuous aerosol flow passes a small cell which is illuminated by a vertical laser beam. When illuminated by the horizontal laser beam, the particles move in the direction of the light. The motion of the particles is observed with a video camera. The path of the particles is shown on the right.
The force on a charged particles in the field of a capacitor offers the possibility to directly measure the photophoretic force. A capacitor having a homogeneous field does not allow a stable positioning of the particles perpendicular to the electric field. By using a capacitor with an insulated inner circular electrode at a higher voltage, a potential well can be created, keeping the particles horizontally stable in the center. Vertical stability is attained by observation of the particle’s location with a position-sensitive detector and a feedback to the voltage of the central plate (Arnold et al., 1980, see Fig. 15).
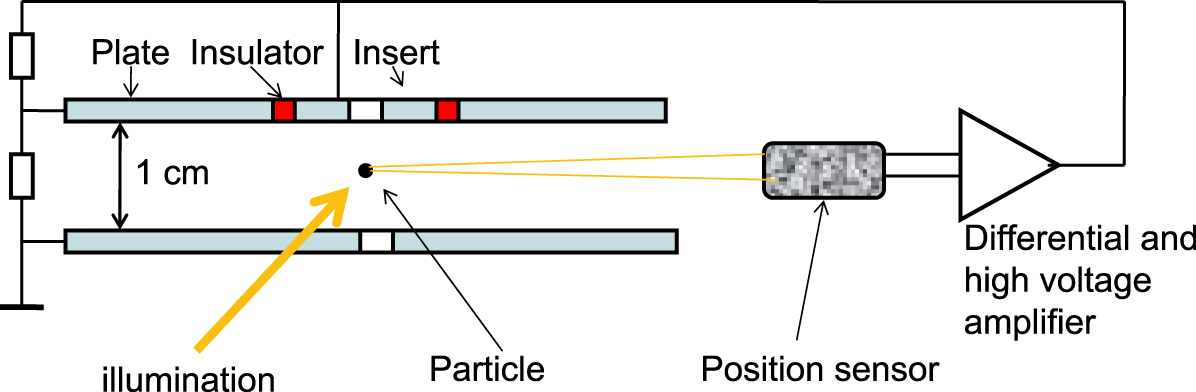
Capacitor for measurement of the photophoretic force. The upper plate of the capacitor has a circular insert, which is kept at a higher voltage, stabilizing the particle horizontally in the center. The vertical stabilization is done with a position-sensitive photodetector.
The electrodynamic levitation (e.g. Wuerker et al., 1959, see also Fig. 16, many other configurations are in use, for a review see, e.g. Davis, 1997) offers the possibility of trapping the charged particles. The AC voltage 2 Vac is applied between the ring electrode and the bottom and top electrode. Additionally, the DC voltage 2 Vdc is added. The non-uniform alternating field has a focusing effect and dynamically stabilizes the charged particle in the null point of the field. The additional DC field compensates the weight of the particle and brings it to the plane of symmetry of the electrodes. When illuminating the particle, e.g. by a vertical laser beam, the DC voltage Vg is adjusted to compensate the additional photophoretic force in order to keep the particle in position. The additional electric field multiplied by the particle charge equals the photophoretic force. For an application see, e.g. Wurm and Krauss (2008).
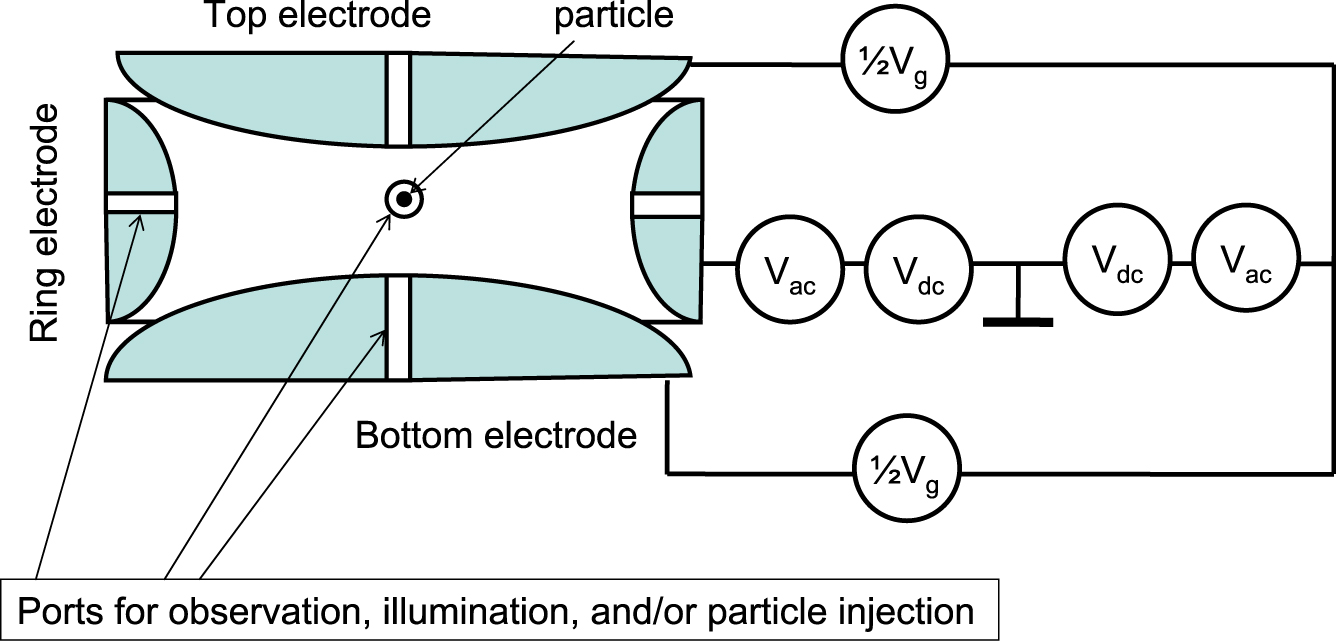
Electrodynamic levitation of particles. An AC voltage is applied between the bottom and top electrode and the ring electrode in series with a DC voltage. By proper shaping of the electrodes, a rotational symmetric parabolic potential is created, trapping the charged particle in the center. When illuminated by a vertical beam, the position of the particle changes. By adjusting Vg, the particle is brought back into position and the force can be determined.
For measurement of field photophoresis, an orienting field is obviously needed. For magneto-or electro-photophoresis this field can be simply generated in the laboratory, whereas the gravitational field is omnipresent. Magneto-photophoresis has, e.g. been measured by Steipe (1952) and Preining (1953), using an arrangement similar to that in Fig. 13, with Helmholtz coils to produce the magnetic field, or to compensate the earth’s magnetic field. The particles were generated by an arc discharge between iron electrodes, producing spherical particles of ferromagnetic iron oxides with a diameter around 400 nm and illuminated with flux densities comparable to the solar constant. The measured photophoretic velocities increased with increasing magnetic field strength due to better orientation. In the case of perfect orientation, the photophoretic velocities were between 50 and 300 μm/s, compared to the settling velocities between 6 and 30 μm/s. For a field strength equaling the earth’s magnetic field, the photophoretic velocities were 50 to 80% of the maximum values, indicating that photophoretic levitation is possible in the atmosphere.
Since gravity cannot be switched on and off, the measurement of gravito-photophoresis is more elaborate (see, e.g. Jovanović, 2005, Fig. 17): An observation cell which can be evacuated has four windows. The illumination comprises a Xenon arc lamp (similar to daylight) and a lens system, producing a homogeneous illumination within the cell comparable to sunlight. A mirror opposite to the light entrance produces additional illumination, reducing longitudinal photophoresis. Observation is perpendicular to the illumination through a microscope lens and a CCD camera. The particle reservoir contains a powder of soot or graphite, etc. Tapping on the reservoir produces about 1000 particles which fall into the beam, a few of them show gravito-photophoresis, move upwards, and end their motion at the top of the illumination beam. The shutter is closed for a few seconds, the particles sediment and upon illumination move upwards again. In this way the velocity due to sedimentation and photophoresis can be measured. An electron microscope grid (normally shielded) can be positioned under the observation volume and the particles can be analyzed. Fig. 18 gives the relation between the Feret diameter and the perimeter of the particles, the particles showing gravito-photophoresis have a larger perimeter, i.e. have a more irregular shape, as expected. Spherical black carbon particles (obtained by the atomization of India ink) do not show gravito-photophoresis.

Measurement of gravito-photophoresis. The cell is illuminated by light through one of the windows, and observation is perpendicular to this direction. Particles in the reservoir are released by knocking the cell slightly. Particles which show photophoresis are trapped at the top of the beam. Closing the shutter causes the particles to sediment, with open shutter the gravito-photophoretic velocity can be measured (Jovanović, 2005).
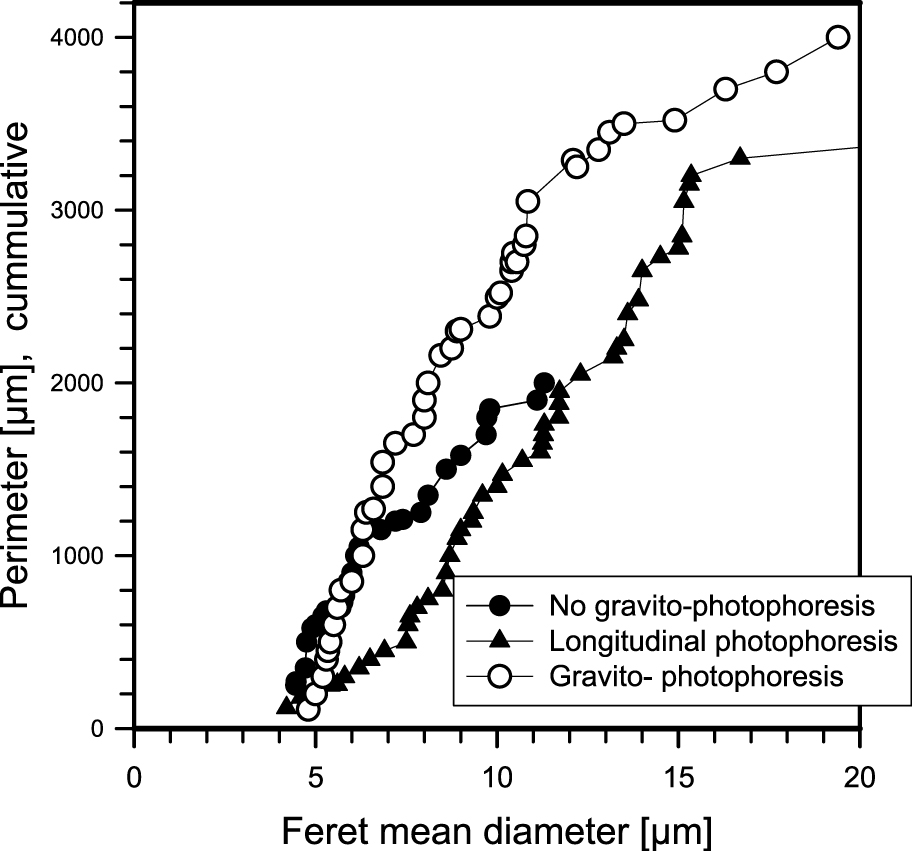
Relation between the Feret diameter and perimeter of particles. The particles showing gravito-photophoresis have the largest perimeter, i.e. are the most irregular (Jovanović, 2005).
Positive photophoresis can be used as a tool for the on-line separation of absorbing and non-absorbing particles. Particles are illuminated by an intense laser (808 nm), obtain a velocity in the direction of the light and perpendicular to the flow velocity due to the photophoretic force, and can be collected in a secondary flow (Haisch et al., 2008). Photophoretic particle trapping in a doughnut-shaped light intensity field and levitation is also possible (Desyatnikov et al., 2009).
Failures in electronic chip production are caused by particles which settle on the chip during production. Shielding the product from the unwanted contamination is traditionally achieved by thermophoretic or electrophoretic forces; but both interfere with the production process. Longitudinal photophoresis has been investigated as a possibility to push particles out of the sensitive range (Selvaraj, 1994; Periasamy et al., 1993). Since the only requirement for photophoresis is a light (laser) beam, interference with the production process is minimal. Furthermore, the photophoretic force increases with decreasing pressure for the particles of interest.
In the stratosphere and mesosphere, the air molecule’s mean free path is between 1 and 100 μm due to the lower pressure, thus appreciable photophoresis can occur for all particles found there. Early laboratory investigations under stratospheric conditions revealed considerable upwards motion of NaCl particles by negative longitudinal photophoresis (Orr and Keng, 1964); on the other hand, Hidy and Brock (1967) estimate the effect of photophoresis on the settling velocity of the particles as negligible. Since an irregular particle or one with a magnetic or electric dipole moment has a preferred orientation in the gravitational, magnetic or electric field, gravito-magneto-or electro-photophoresis are important. This has been proven experimentally (Jovanović, 2005).
The existence of layers of particles in the stratosphere and mesosphere is a well-known fact (Junge et al., 1961; Bigg, 1964; Volz, 1971; Zuev et al., 1996, 2009; Berthet et al., 2002, Mateshvili et al., 1999; Gerding et al., 2003). Furthermore, soot particles are found at locations in the stratosphere with no evident sources (Pueschel et al., 2000). Soot particles absorb light, thus are hotter than the surrounding air, and they have a complex shape, which is important for gravito-photophoresis. So the movement of the particles upwards from the place where they are produced (Pueschel et al., 2000) can be explained. For the existence of particle layers in the atmospheres, it is necessary that (1) a lifting force on the particles compensates gravity and (2) that the particles return to their location after disturbance. Due to the complex structure of the stratosphere and mesosphere, locations can be found where these requirement are fulfilled (Cheremisin et al., 2005, 2011). The particles are illuminated by solar radiation amounting to 1360 W/m2, thus light-absorbing particles consisting of black carbon or iron oxides can be levitated by gravito-, electro- or magneto-photophoresis. The outgoing terrestrial infrared radiation equals the solar constant, thus particles that are transparent in the visible but absorbing in the infrared are also candidates for photophoresis. For example, for ammonium sulfate, the imaginary part of the refractive index is < 10−6 in the visible but increases to more than 1.0 at 10 μm, thus (NH3)2SO4 is as absorbing in the infrared as black carbon in the visible (Bohren and Huffman, 1983, p. 438). In the Junge layer (Junge et al., 1961), sulfate particles have been found and Cheremisin et al. (2011) have shown that particles which strongly absorb in the infrared only and sized between 1 and 2 μm will be stable at ≈ 22 km. Particles formed from meteor smoke or debris of rockets can have a magnetic momentum and thus be oriented by the earth’s magnetic field. The magnetic orientation is stronger than by gravity, see Fig. 10, so particles between 0.1 and 0.25 μm can form layers, e.g. at 76 to 82 km. Favorable conditions in the atmosphere for the formation of stable layers depend on time, latitude, longitude, and particle size. Particles with sizes between 0.1 and 5 μm can form layers between 18 and 90 km altitude at various times of the year, latitude and longitude. For details see Cheremisin et al. (2011). A comparison of the backscatter ratio of the Kamchatka LIDAR station 2007 to 2008 and the calculated stability zones shows an almost perfect agreement (Cheremisin et al., 2012).
Photophoresis can have an influence on coagulation: After reflection from the surface of a particle heated by light absorption, the gas molecules have a higher velocity, they can repel adjacent particles by impaction and thus slow coagulation (Cheremisin and Kushnarenko, 2013). The magnitude of the force is considerable and comparable to electrostatic forces: e.g. two 50-nm particles separated by three radii, illuminated by 1360 W/m2 at a pressure of 1000 Pa, the repelling force is 30 times the weight of the particles, for 250- and 500-nm particles the factors are 10 and 7. At night, the particles are colder than the surrounding air and thus have a small attractive force. This repelling force slows coagulation, the coagulation constant is reduced by a factor of up to 10.
During combustion, the high temperatures cause strong infrared and visible radiation, and light-absorbing particles are present. The main force on the particles is by thermophoresis powered by the temperature gradients, but the photophoretic forces cannot be neglected. They are responsible for the formation of stable soot shells around a fuel droplet (Pera et al., 1999), and amount to about 10% of the deposition force to cold surfaces (Castillo et al., 1990).
Photophoresis is an important force involved in planet formation. In a gas-rich, optically thin circumstellar disk, the motion of particles ranging from 1 μm to 10 cm will be dominated by photophoresis, moving the particles opposite to gravity to a distance from the star where the gas density reaches a value at which photophoresis equals all other forces at work. Thus the formation of ring-like structures of dust distribution around a star can be explained naturally (Krauss and Wurm, 2005), and the formation of protoplanets is significantly influenced by photophoresis (Wurm and Krauss, 2006; Krauss et al., 2007).
In the fight against global warming by geo-engineering, particles could be positioned in the stratosphere or mesosphere. They should reflect sunlight and remain suspended as long as possible. The photophoretic force can be very helpful, since a long residence time can be achieved this way. A particle optimized for this purpose could be a disk of 10 μm in diameter, having a layer of Al2O2 at the top, Al in the middle and BaTiO3 at the bottom and a thickness of 10 nm. Orientation is caused by the electric field (Keith, 2010), i.e. electro-photophoresis prevents settling.
For completeness it is mentioned that the term photophoresis is also used for the motion of hydrocolloids illuminated by an intense laser beam. But for photophoresis, the thermal slip is needed. In that case, it is actually the radiation pressure, see Eqn. (1), that makes the particle migrate (Helmbrecht et al., 2007).
The author is thankful for the infrastructure made available by Professor Tohno, School of Energy Science of the University of Kyoto and the Zentralbiliothek für Physik Wien, which is an almost infinite source for hard-to-find literature. Most of this paper was presented as a plenary lecture during the European Aerosol Conference 2012 in Granada. I thank the organizers L. Alados and F.J Olmo Reyes for giving me the chance to investigate this interesting subject in depth.
| Symbol | Name | Unit | Definition | Remark |
|---|---|---|---|---|
| A | Absorption cross-section | m2 | |
Fictitious surface through which the absorbed light passes |
| B | Magnetic flux density | T | ||
| c̄ | Mean velocity of gas molecules | m·s−1 | |
|
| Cs | Slip correction | none | ||
| d | Diameter | m, μm, nm | ||
| Eemitt Eabs | Emitted, absorbed IR flux | W | IR flux absorbed and emitted by a particle; must be balanced with absorbed visible flux and power transferred by accommodation to molecules | |
| g | Gravity constant | m·s−2 | g ≈ 10m·s−2 | Acceleration on earth due to gravity |
| H | Transferred energy flux | W | Energy flux transferred by the gas molecules from the particle surface | |
| J1 | Asymmetry parameter for absorption | none | Yalamov et al., 1976 | |
| k | Boltzmann constant | J·K−1 | k = 1.38·10−23 J·K−1 | |
| kg kp | Thermal conductivity | W·m−1·K−1 | kg conductivity of gas, kp conductivity of particle’s material | |
| L(x) | Langevin function | none | |
|
| M | Molecular mass | kg·kMol−1 | ||
| m | Magnetic moment | Am2 | Symbol m also used for mass | |
| p | Pressure | Pa | ||
| q | Displacement | m | Vector between center of gravity and center of photophoretic force | |
| Qe | Absorption efficiency | none | Absorbed radiation divided by the radiation incident on the particle | |
| R | Gas constant | R = 8314 J kMol−1 K−1 | ||
| S | Flux density | W·m−2 | |
Energy of radiation passing per time through a surface |
| T | Absolute temperature | K | ||
| x | none | |
Ratio of potential energy Ep = m·B or Ep = m·g·q and thermal energy Eth = k·T | |
| α | Accommodation coefficient | none | |
Probability for a gas molecule to diffusely reflect from the particle’s surface with the temperature of the surface |
| γ | none | |
Ratio of specific heat at constant pressure and specific heat at constant volume | |
| η | Viscosity | Pa·s | ||
| κ | Thermal creep coefficient | none | κ = 1.14 for 10% specular-reflected molecules | |
| ρ | Density | kg·m−3 | ρp density of material-forming particle | |
| |
Square of angular displacement | rad2 | |
The mean square angle of rotation in time t |
Helmuth Horvath
Helmuth Horvath, born 1941 in Vienna, studied experimental physics in Vienna, Ph.D. in 1966 under the guidance of O. Preining. Extended scientific visits with the universities of Washington, Colorado, Santiago de Chile, Kyoto and Granada. Professor of Experimental Physics in Vienna 1980 to 2006. Research interest in all aspects of the physics of aerosols, especially optics.