Self-Propelled Nano/Micromotors with a Chemical Reaction: Underlying Physics and Strategies of Motion Control

Abstract

Nano/micromotors exhibiting regulated motions are ubiquitous in nature, with biological ones having highly sophisticated and functional properties. However, nano/micromotors have not been applied in the design of useful man-made chemical systems to our knowledge. In this article, we review artificial nano/micromotors that have been proposed in the last decade. The underlying physics is completely different from that of conventional macroscale motors. The viscous force dominates the regulated motion of a nano/micromotor, in which thermal fluctuation converts into active Brownian motion. To overcome the viscous force and sustain motion, motors driven by various types of mechanisms have been fabricated. We focus on chemical reaction propelled motors classified into catalytic and self-reacted ones because most biomotors move by consuming chemical energy. Furthermore, the directional control of artificial nano/micromotors by chemotaxis, external field, and confined space is also discussed. As this hot and challenging topic is still currently at a fundamental stage, practical research will be required for developing various applications. We expect that chemical systems mimicking elegant biological ones will be realized in the near future.

1. Introduction

1.1 What is a nano/micromotor?

What kind of scientific principle do we associate with the phrase “transfer of nano/micro particles”? In this article, the authors suppose that the readers are chemical engineers, especially engaged in powder technology. As such, most of us are often reminded of translation along a chemical potential gradient, such as sedimentation/floatation under a gravitational field (Svarovsky, 1981), electrophoresis under an electric field (Westermeier, 2006), magnetophoresis under a magnetic field (Lim et al., 2011; Suwa and Watarai, 2011), and diffusion under a concentration gradient (Cussler, 2009). This translation arising from a chemical potential gradient formed by external fields is called “passive motion,” where objects move monotonously from an area or state of higher chemical potential to that of a lower one.

In contrast, self-propelled nano/micro objects that can overcome the chemical potential gradient are ubiquitous in our bodies, and play a crucial role in vital actions (Fig. 1). For example, in a process called “chemotaxis,” a white blood cell chases a bacterium by sensing irritants that it produces, such as N-formylated peptides (Fenteany and Glogauer, 2004). A kinesin, which is one of the motor proteins in the cell of living organisms, carries a biogenic object, and moves toward the destination along a microtubule using chemical energy released by the decomposition of adenosine triphosphate (ATP) (Kanai et al., 2004; Vale et al., 1996). These biological systems can convert chemical energy into mechanical work, leading to more sophisticated functional motions than the “passive motion” described above. Such a self-motile nano/micro object, and a spontaneous motion that is independent of a chemical potential gradient are called “nano/micromotor,” and “active motion”, respectively (Romanczuk, 2011).

Fig. 1

Examples of autonomous motions of biological systems. (a) Bacterial phagocytosis (meaning “to devour”) of a white blood cell, and (b) mass transfer by a motor protein in a cell cytoplasm.

1.2 A new transport phenomena in chemical engineering

“Active motion” is a common topic in mechanical engineering (Zhang et al., 2010), biology (Campuzano et al., 2011), and non-linear science (Strogatz, 1994); however, most chemical engineers do not seem to be acquainted with it. To the authors’ knowledge, nano/micromotors have not been applied to the design of chemical systems since chemical engineering was established half a century ago. This is no wonder, since chemical engineering has developed based on monotonous dynamics to thermodynamic equilibrium (Bird et al., 2007). It has often been the case for chemical engineers that numerous dynamics related to chemical processes proceed monotonously toward thermodynamic equilibrium. However, the degrees of freedom for chemical system design will increase dramatically if these new “transport phenomena” are incorporated into the design. We believe this forecast by taking into account the recent progresses in biology that reveal a vast number of wonderful characteristics of living matter as a chemical system (Phillips et al., 2009).

We expect a rich variety of possible applications as depicted in Fig. 2. For example, if catalytic particles can move against the concentration gradient of reactants like the chemotaxis of a white blood cell, the catalytic activity will increase, not by catalyst chemistry, but by its mobility if the overall reaction order is greater than one. Furthermore, higher-order reactions will yield more remarkable differences from a conventional catalyst because the reaction rate depends more strongly on concentration. In addition, these micro motors may be used as a power source for micromachines and microfactories. For instance, a motor that shows rotation or spin motion might be applied to a microcarrier or micropump, which is ubiquitous in our bodies, for example, a motor protein (Vale and Milligan, 2000), or an ion pump in cells (Blaustein and Lederer, 1999).

Fig. 2

Possible applications of nano/micromotors.

In this article, we review artificial nano/micromotors and focus on chemical reaction driven ones because these seem to exhibit a biomimetic function with potential applications to chemical systems. For example, these motors may move by responding to surrounding chemicals and migrating along the concentration gradient. Firstly, we discuss the underlying physics of nano/micromotors compared to conventional macro motors (Sec. 2). Secondly, we introduce examples of artificial nano/micromotors propelled by various types of mechanisms (Sec. 3). Finally, we focus on reaction-propelled motors and their directional control (Secs. 4 and 5).

2. Physics of nano/micromotors

A moving macro object can maintain its motion without continuous force for an extended period of time even under a viscous drag, while a nano/micro scale object cannot be due to the crucial effect of viscous force. Furthermore, thermal fluctuation, which is caused by collisions with the surrounding molecules, becomes more significant with a decrease in size. This section presents a theoretical and quantitative discussion of the motions of nano/micro objects. Although these concepts are rudimentary to physics, explicit descriptions related to nano/micromotors are rarely seen to the authors’ knowledge. In Secs. 2.2 and 2.3, theory and equations based on Stokes’ law will fail under the situation where a solvent behaves as a discontinuous one, that is, with a smaller nano-sized object or at gas phase. Nevertheless, they are useful enough to estimate order of magnitude roughly even under such a situation.

2.1 Reynolds number

In general, inertia and viscous force dominate the motion of macro and nano/micro scale objects. For a moving object of characteristic length L with velocity v, the Reynolds number Re, which represents the ratio of inertia to viscous force, is defined as   

$$\mathit{Re}=\frac{\mathit{Inertia}}{\mathit{Viscous}\hspace{0.17em}\mathit{force}}=\frac{\rho v^2}{\mu v/L}=\frac{\rho vL}{\mu }=\frac{vL}{\upsilon }$$(2.1)

where ρ, μ, and υ are the density, dynamic viscosity, and kinematic viscosity of the medium, respectively. Table 1 shows examples of Reynolds numbers of self-propelled objects in water and air. Although water and air have quite different densities (ρ_water ≈ 1.0 × 10³ kg/m³, and ρ_air ≈ 1.2 kg/m³) and dynamic viscosities (μ_water ≈ 1.0 mPa·s, and μ_air ≈ 0.018 mPa·s), kinematic viscosities are similar to some extent (υ_water ≈ 1.0 × 10⁻⁶ m²/s, and υ_air ≈ 1.5 × 10⁻⁵ m²/s). In addition, the smaller object usually has the slower velocity, as demonstrated by allometric laws, such as the swimming speed of fish (Bainbridge, 1958), running speed of mammals (Garland, 1983) and cruising speeds of flying animals, and vehicles (Tennekes, 1997). Therefore, the size is a crucial factor determining which of the two forces is dominant (see Table 1). If this boundary is set at Re = 1, then a motile object having a size below the submillimeter scale is influenced strongly by viscosity.

Table 1 Reynolds numbers of self-propelled organisms and artifacts

Motile object	Mediuma	Size scale [m]	Velocity scale [m/s]	Reynolds number [–]
Large submarine	Water	∼102	∼101	∼109
Whaleb	Water	∼101	∼101	∼108
Tunab	Water	∼100	∼101	∼107
Human (swimming)	Water	∼100	∼100	∼106
Sparrow	Air	∼10−1	∼101	∼105
Killifish	Water	∼10−2	∼10−1	∼103
Water flea	Water	∼10−3	∼10−2	∼101
Flyb	Air	∼10−3	∼10−1	∼101
Paramecium	Water	∼10−4	∼10−3	∼10−1
Sea urchin spermb	Water	∼10−4	∼10−5	∼10−3
Bacteriumb	Water	∼10−6	∼10−5	∼10−5
Artificial nano/micromotorc	Water	∼10−6	∼10−5	∼10−5

a  Kinematic viscosities (ν = μ/ρ) of water and air are set to ∼10⁻⁶ m²/s and ∼10⁻⁵ m²/s, respectively.

b  The data are estimated based on the previous book (Vogel, 1994).

c  The data are those of the earliest artificial nano/micromotor (See Secs. 3 and 4) (Paxton et al., 2004). However, note that other motors have almost the same scales of size and velocity as shown in Table 3.

Unlike currently available macro motors, a nano/micromotor should exhibit high performance under the condition that the viscous drag overcomes inertia, i.e., ultralow Reynolds numbers (Re « 1). In this regime, the strategy of simple downsizing of macro motors cannot be applicable. Even if a conventional mechanical motor is downsized to the micron size, one has to supply a large amount of energy to maintain its mobility. Such a large energy input into a small system is inefficient and may destroy the system. Of course, assembling a small mechanical system is also quite difficult from a practical point of view.

2.2 An equation of translational motion

Newton’s second law states that the net force (F_net) acting upon an object is equal to the time (t) derivative of its momentum. If the mass (m) of the object is constant, the equation for translation is   

$$m\frac{\text{d}v}{\text{d}t}=F_{\text{net}}$$(2.2)

where v denotes the velocity of the object. Here, let us consider that the driving force (F_d) and drag force (F_η) constitute the net force. Eqn. 2.2 is described as   

$$m\frac{\text{d}v}{\text{d}t}=F_{\text{d}}-F_{\eta }$$(2.3)

For a spherical object of diameter d_p, the drag force is defined as   

$$F_{\eta }=C_{\text{D}}\cdot \left(\frac{1}{2}\rho v^2\right)\cdot \left(\frac{1}{4}\pi {d_{\text{p}}}^2\right)$$(2.4)

Here, C_D is the drag coefficient, which is a function of the Reynolds number (i.e., a function of velocity). The relationship between C_D and Re for a spherical object was obtained experimentally (Schlichting, 1955) and approximated by   

$$C_{\text{D}}=\frac{24}{\mathit{Re}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(\mathit{Re}<1,\hspace{0.17em}\hspace{0.17em}\text{Stokes}\hspace{0.17em}\hspace{0.17em}\text{flow}\right)$$(2.5)

  

$$C_{\text{D}}=\frac{10}{\sqrt{\mathit{Re}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(1<\mathit{Re}<500,\hspace{0.17em}\hspace{0.17em}\text{Allen}\hspace{0.17em}\hspace{0.17em}\text{flow}\right)$$(2.6)

  

$$C_{\text{D}}=0.44\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(500<\mathit{Re}<{10}^5,\hspace{0.17em}\hspace{0.17em}\text{Newton}\hspace{0.17em}\hspace{0.17em}\text{flow}\right)$$(2.7)

Because nano/micromotors have ultralow Reynolds number, the drag force is evaluated from Eqns. 2.4, 5 as follows:   

$$F_{\eta }=3\pi \mu d_{\text{p}}v\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(\text{Stokes}\text{'}\hspace{0.17em}\hspace{0.17em}\text{law}\right)$$(2.8)

From Eqns. 2.3, 8, the equation of translational motion for a nano/micro object is expressed by   

$$m\frac{\text{d}v}{\text{d}t}=F_{\text{d}}-3\pi \mu d_{\text{p}}v$$(2.9)

If F_d is constant, the differential equation can be analytically integrated for a finite change in velocity from v₀ at t = 0 to v at an arbitrary time t:   

$$v(t)=(v_0-v_{\text{f}})e^{-\frac{t}{\tau }}+v_{\text{f}}$$(2.10)

The terminal velocity v_f and relaxation time τ are given respectively by   

$$v_{\text{f}}=\frac{F_{\text{d}}}{3\pi \mu d_{\text{p}}}$$(2.11)

and   

$$\tau =\frac{m}{3\pi \mu d_{\text{p}}}=\frac{\frac{\pi }{6}{d_{\text{p}}}^3{\rho }_{\text{p}}}{3\pi \mu d_{\text{p}}}=\frac{{d_{\text{p}}}^2{\rho }_{\text{p}}}{18\mu }$$(2.12)

where ρ_p represents the density of the particle. When the values are ρ_water ≈ 1.0 × 10³ kg/m³, μ_water ≈ 1.0 mPa·s, and μ_air ≈ 0.018 mPa·s, Eqn. 2.12 is approximated by   

$$\tau \approx 0.056SG\times {\left(d_{\text{p}}/\text{mm}\right)}^2[\text{s}]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(\text{in}\hspace{0.17em}\text{water})$$(2.13)

  

$$\tau \approx 3.1SG\times {\left(d_{\text{p}}/\text{mm}\right)}^2[\text{s}]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(\text{in}\hspace{0.17em}\hspace{0.17em}\text{air}),$$(2.14)

where SG is the specific gravity (ρ_p/ρ_water) of the spherical particle.

The time (t_±99%) required to proceed from v₀ = 0 to 0.99v_f with constant driving force and v₀ ≠ 0 to 0.01v₀ without driving force are calculated from Eqns. 2.3–7, and shown as a function of Re in Fig. 3. At Re < 1, the time required to proceed from v₀ = 0 to 0.99v_f with the constant force is   

$$t_{99\%}=\text{ln}100\times \tau$$(2.15)

Fig. 3

Relationship between Reynolds number and time t_±99% required to proceed from v₀ = 0 to 0.99v_f (with constant force), and v₀ ≠ 0 to v_f = 0.01v₀ (without constant force). The graph was calculated from Eqns. 2.3–7. The relaxation time τ for each flow was given by Eqn. 2.12. Terminal velocities v_f were obtained from Eqns. 2.12, 16, 17 for Stokes, Allen, and Newton flows, respectively.

Note that Eqn. 2.10 is not applicable to macro motors, which moves in Allen and Newton flows. Hence, v_f and t_99% are instead estimated as follows:

• A) Allen flow,   
  $$v_{\text{f}}=\sqrt[3]{\frac{16{F_{\text{d}}}^2}{25{\pi }^2\mu \rho }}\times {d_{\text{p}}}^{-1}$$(2.16)
    
  $$t_{99\%}\approx 7.87{\mathit{Re}}^{-0.5}\times \tau$$(2.17)
• B) Newton flow,   
  $$v_{\text{f}}=\sqrt{\frac{F_{\text{d}}}{0.055\pi \rho }}\times {d_{\text{p}}}^{-1}$$(2.18)
    
  $$t_{99\%}\approx 143{\mathit{Re}}^{-1}\times \tau$$(2.19)

According to Eqns. 2.13, 15, if a constant driving force acts on a particle with a diameter of 1 μm, its motion immediately reaches the terminal velocity (< 1 μs). This is why the translational motion of a nano/micro object is often discussed with $m\frac{\text{d}v}{\text{d}t}=0$ even if the driving force varies with time (Takinoue et al., 2010), as well as why the terminal velocity, such as sedimentation velocity and electrophoretic mobility, plays a more decisive role than transient velocity (Dueck, 2013).

Fig. 3 also demonstrates that the translational motion with velocity v₀ of a nano/micro object is immediately damped by the surrounding viscosity and transformed into thermal fluctuation, i.e., Brownian motion. Therefore, a sustained motion of nano/micromotor requires a continuous driving force.

For other types of regulated motion, such as spin or rotation, a non-zero torque N is required, which is defined as the vector product of the displacement and force vectors. The equation for rotation is   

$$I\frac{\text{d}\omega }{\text{d}t}=N_{\text{d}}-N_{\eta }$$(2.20)

Similarly to Eqn. 2.3, N_d and N_η are the torque arising from the driving force and drag force, respectively. I and ω represent the moment of inertia and angular velocity. We assume that rotation is restricted on the x–y plane, and the torque vector only has a z-component. Essentially the same discussion can be made in the case of translation. The important conclusions are as follows, although the details are not mentioned:

• 1) Eqn. 2.20 should be calculated as $I\frac{\text{d}\omega }{\text{d}t}=0$ for a nano/micromotor.
• 2) A spinning nano/micromotor requires continuous torque to maintain its motion.

2.3 Thermal fluctuation

The smaller particle is strongly influenced by thermal fluctuation, leading to random Brownian motion. Let us consider the two-dimensional motion (x–y plane) of a nano/micro-sized Janus motor propelled by a constant driving force F_d toward the azimuth ϕ(t) as shown in Fig. 4a. A typical Janus particle is a spherical one composed of two hemispheres with different properties. Unless thermal fluctuation affects the motion, the particle shows translation toward the direction of the initial azimuth ϕ(0). At an ultralow Reynolds number, each acceleration term is neglected ( $m\frac{\text{d}v}{\text{d}t}=0$, $I\frac{\text{d}\omega }{\text{d}t}=0$) as discussed in Sec. 2.2. In this case, the equations of motion for translation and rotation, i.e., Langevin equations (Uhlenbeck and Ornstein, 1930), are expressed by Eqns. 2.21–23 as follows:   

$${\gamma }_{\text{T}}\frac{\text{d}x}{\text{d}t}=F_{\text{d}}\text{cos}\varphi +{\xi }_x(t)$$(2.21)

  

$${\gamma }_{\text{T}}\frac{\text{d}y}{\text{d}t}=F_{\text{d}}\text{sin}\varphi +{\xi }_y(t)$$(2.22)

  

$${\gamma }_{\text{R}}\frac{\text{d}\varphi }{\text{d}t}={\xi }_{\text{R}}(t)$$(2.23)

The subscripts T and R denote translation and rotation, while γ_T and γ_R are the friction coefficients. In the case of a spherical particle with Re « 1, these are given by   

$${\gamma }_{\text{T}}={\gamma }_x={\gamma }_y=3\pi \mu d_{\text{p}}$$(2.24)

  

$${\gamma }_{\text{R}}=\pi \mu {d_{\text{p}}}^3$$(2.25)

ξ_x(t), ξ_y(t), and ξ_R(t) are the thermal noise or Gaussian white noise with zero mean (Horsthemke, 1984). These are characterized by   

$$⟨{\xi }_i(t_1)⟩=0$$(2.26)

  

$$⟨{\xi }_i(t_1){\xi }_i(t_2)⟩=2{\gamma }_i{k}_{\text{B}}T\delta (t_1-t_2)$$(2.27)

where the subscript i means x, y, or R. δ is the Kronecker delta, and ⟨...⟩ denotes an ensemble average. k_B and T are the Boltzmann’s constant and absolute temperature, respectively. According to the Einstein–Smoluchowski relation (Einstein, 1905, Von Smoluchowski, 1906), the diffusion constant D_i is obtained from   

$$D_i=\frac{k_{\text{B}}T}{{\gamma }_i}$$(2.28)

According to a previous paper (Ten Hagen et al., 2011), the mean-square displacement (MSD) ⟨r²⟩ is given by the integration of Eqns. 2.21–23 as   

$$⟨r^2⟩=\frac{4}{3}{d_{\text{p}}}^2{D}_{\text{R}}t+2{\left(\frac{v_{\text{f}}}{D_{\text{R}}}\right)}^2\times \left(D_{\text{R}}t-1+e^{-D_{\text{R}}t}\right)$$(2.29)

where v_f is the terminal velocity given by Eqn. 2.11. Eqn. 2.29 is reduced to   

$$⟨r^{*2}⟩=\frac{4}{3}{t}^{*}+2v_{\text{f}}^{*2}\times \left(t^{*}-1+e^{-t^{*}}\right)$$(2.30)

The reduced parameters are $r^{*}=\frac{r}{d_{\text{p}}}\left(r=\sqrt{{\left[x(t+t_{\text{a}})-x(t_{\text{a}})\right]}^2+{\left[y(t+t_{\text{a}})-y(t_{\text{a}})\right]}^2}\right)$ (t_a: arbitrary time), $v_{\text{f}}^{*}=\frac{v_{\text{f}}}{d_{\text{p}}{D}_{\text{R}}}$, and t* = D_Rt. Fig. 4b shows the relationships between t* and ⟨r^*2⟩ at various $v_{\text{f}}^{*}\text{s}$. When the Brownian motion dominates (F_d does not work or is negligibly small compared to thermal noise ξ; $v_{\text{f}}^{*}«1$), Eqn. 2.30 approximately becomes the Einstein-Smoluchowski equation in two-dimensional space as follows:   

$$⟨r^{*2}⟩\approx \frac{4t^{*}}{3}\iff ⟨r^2⟩\approx \frac{4}{3}{d_{\text{p}}}^2{D}_{\text{R}}t=4D_{\text{T}}t$$(2.31)

Fig. 4

(a) Model of a Janus motor propelled by a constant force toward the specific direction. (b) Relationship between reduced time and mean-square displacement (MSD) at various v_f^*s.

With a sufficiently strong constant driving force ( $v_{\text{f}}^{*}>1$), Eqn. 2.26 can be approximated, depending on the time scale as follows:

• (A)Brownian motion   
  $$⟨r^{*2}⟩\approx \frac{4t^{*}}{3}\propto t^{*}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(0<t^{*}<~\frac{1}{v_{\text{f}}^{*2}}\right)$$(2.32)
• (B) Translational motion (linear motion with constant velocity $r^{*}\approx v_{\text{f}}^{*}{t}^{*}$)   
  $$⟨r^{*2}⟩\approx {\left(v_{\text{f}}^{*}{t}^{*}\right)}^2\propto t^{*2}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(~\frac{1}{v_{\text{f}}^{*2}}<t^{*}<~1\right)$$(2.33)
• (C) Active Brownian motion (random walk with active diffusion constant)   
  $$⟨r^{*2}⟩\approx \left(\frac{4}{3}+2v_{\text{f}}^{*2}\right)t^{*}\propto t^{*}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(~1<t^{*}\right)$$(2.34)

Following Eqns. 2.32–34, the dynamical mode changes dramatically depending on the time scale. At the microscopic scale corresponding to the shorter time scale $\left(t<\frac{{d_{\text{p}}}^2{D}_{\text{R}}}{{v_{\text{f}}}^2}\right)$, the self-propelled particle shows thermal Brownian motion. At the intermediate scale $\left(\frac{{d_{\text{p}}}^2{D}_{\text{R}}}{{v_{\text{f}}}^2}<t<{D_{\text{R}}}^{-1}\right)$, it exhibits translational motion with constant velocity v_f, which is the terminal velocity without thermal fluctuation. At the macroscopic scale (D_R⁻¹ < t), it exhibits active Brownian motion, which has a larger diffusion constant than thermal Brownian motion (Jain, 2008). The apparent diffusion constant D_A for translation is obtained from   

$$D_{\text{A}}=D_{\text{T}}+\frac{{v_{\text{f}}}^2}{2D_{\text{R}}}$$(2.35)

Here, D_R⁻¹ of a spherical particle at 298 K is approximated by   

$${D_{\text{R}}}^{-1}\approx 0.76\times {\left(d_{\text{p}}/\mu \text{m}\right)}^3[\text{s}]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(\text{in}\hspace{0.17em}\text{water})$$(2.36)

The above discussion demonstrates that a micro-sized motor with a characteristic length of 1 μm generally exhibits random, instead of translational, motion at a time scale greater than 1 s. Thus, long-distance migration is quite difficult because the average distance with this motion is proportional to t^0.5 (see Eqn. 2.34). In such a case, directional motion, where the distance is proportional to t, is preferred for efficient motion.

2.4 Directional control of continuous regulated motions of nano/micro objects

For a nano/micromotor, the viscous force and thermal fluctuation have a significant influence on its regulated motion as mentioned above. The former damps its motion immediately while the latter converts its motion into active Brownian motion via thermal rotation. In order to control the direction of its translational motion, not only a continuous driving force, but also a response to external stimuli is required. For example, chemotaxis, which is inherent to numerous biological motions, such as a white blood cell or bacterium (Adler and Tso, 1974), may play a significant role in regulated motion toward the destination. In addition, biomotors, such as kinesin and myosin, show directional motion by using a confined space, that is, walking along a monorail (e.g., microtubule or actin), which hinders the change of direction arising from thermal fluctuation (Van Den Heuvel and Dekker, 2007).

An artificial nano/micromotor can exhibit such biomimetic motion because even a molecular-sized biomotor can generate regular motion under viscous force and thermal fluctuation effects that are stronger than those in artificial nano/micromotors. Artificial motor systems propelled by a continuous driving force by various mechanisms are introduced in Secs. 3 and 4. Furthermore, directional control has been attempted for artificial nano/micromotor, which is discussed in Sec. 5.

3. Examples of fabricated artificial nano/micromotors

The preparation of nano/micromotor systems has been a hot and challenging topic in nanotechnology and biotechnology for the last decade. Pioneers in the field are Paxton and coworkers, who demonstrated a nano/microsized motor system with catalytic particles in a solution containing reactants in 2004. The particles exhibit non-Brownian motion by using chemical energy generated by a catalytic reaction. Motors such as these will be discussed in detail in Sec. 4. Since then, several research groups have attempted to fabricate artificial nano/micromotors that employ other mechanisms such as electric, magnetic, and ultrasound propulsions (Fig. 5). Here, we summarize these nano/micromotors before discussing chemical reaction driven motors.

Fig. 5

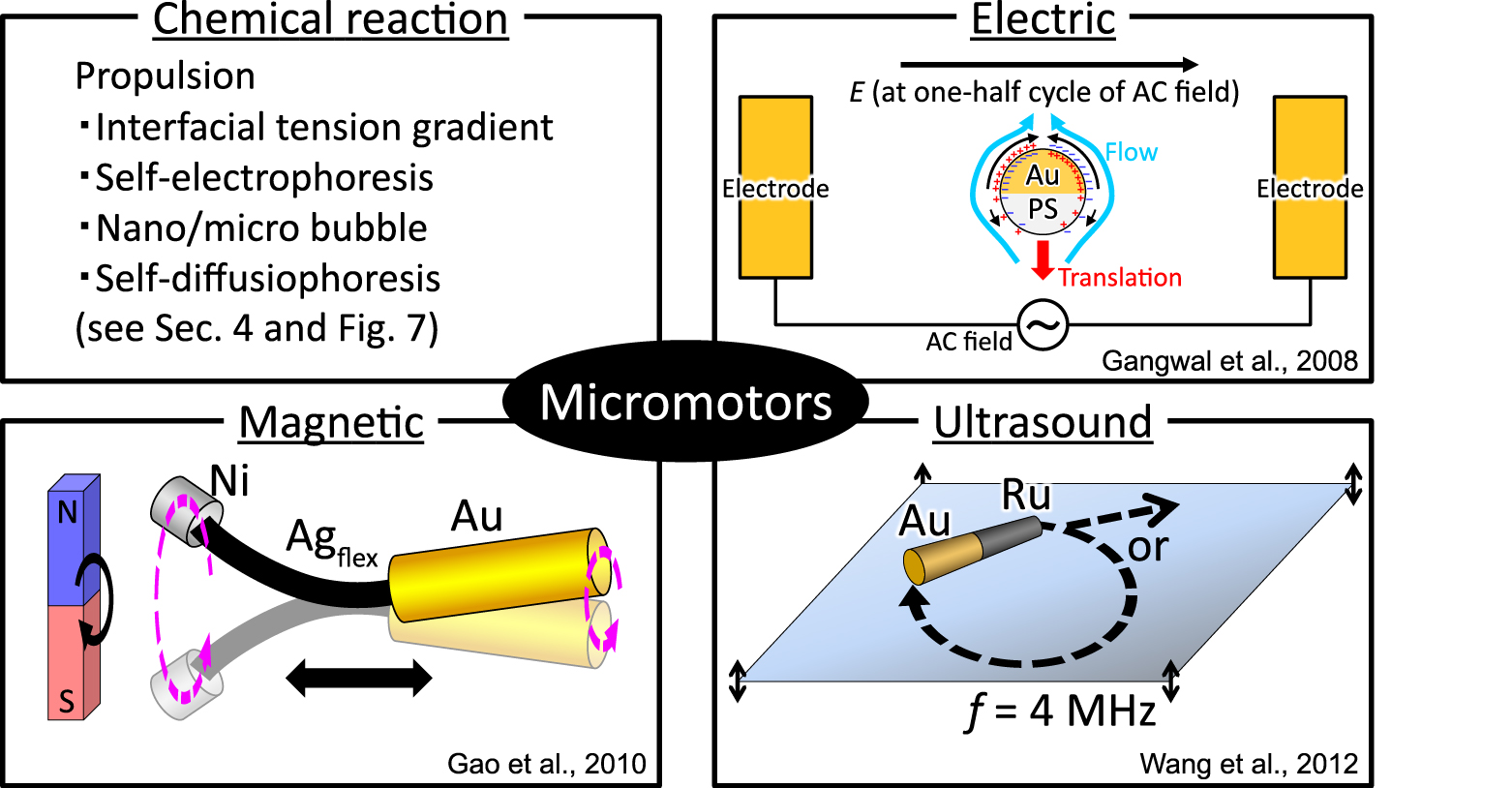
Examples of synthetic micro motors propelled by different mechanisms.

One of the simplest electric-induced motor is a Janus particle made by partially coating a polystyrene (PS) latex sphere with Au (Gangwal et al., 2008). The particle shows translational motion along the direction perpendicular to the AC field. The electric double layer on the Au hemisphere is more strongly polarized, and thus drives a stronger induced-charge electro-osmosis (ICEO) slip, than that on the PS one, resulting in induced-charge electrophoresis (ICEP) motion in the direction of the PS side.

A typical magnetic-driven motor is the composite nanowire with a flexible thin Ag joint connecting the Au head and Ni tail (Au/Ag_flex/Ni nanowire) (Gao et al., 2010). A rotating magnetic field creates a corkscrew rotation of the Ni segment, leading to translational motion along the rotation axis of the magnetic field. Interestingly, the translational direction was changed by tuning the length of the Au and Ni segments. Based on a similar mechanism, a helical motor with Ni/Ti bilayers has been reported (Tottori et al., 2012). The translational motion, converted from rotational motion, mimics bacterial motion by rotating a flagellar filament (Berg and Anderson, 1973). Note that the motion of the above electric/magnetic-driven motor is essentially different from the passive motion of a charged/magnetic particle by electrophoresis/magnetophoresis because the steady gradient of chemical potential does not exist under these switching fields.

An example of an ultrasound-propelled motor is a microrod made of two metal species (Au/Ru or Au/Pt rods) (Wang et al., 2012). When an ultrasonic frequency is tuned to create a vertical standing wave, the rod levitates to the midpoint plane of a cylindrical acoustic cell, and exhibits various kinds of motion (translational motion, rotation, and axial spinning). The asymmetric shape of the metal rod can lead to an asymmetric distribution of the acoustic pressure from the scattering of the incident acoustic waves at the metal surface (called self-acoustophoresis), which produces the above dynamic mode.

In general, the shape and chemical composition of these nano/micromotors are designed so as to break the symmetry of the local field to generate a gradient (Wang et al., 2013). Note that the term “symmetry breaking” is a notion widely accepted in physics (Anderson, 1972). Therefore, most of these previous nano/micromotors possess compositional asymmetry to gain the continuous driving force or torque required for motion toward a certain direction.

4. Nano/micromotors driven by chemical reactions

Nano/micromotors driven by chemical reactions are classified into two groups: a catalytic motor and a self-reacted one. The former shows semi-permanent motion so long as reactants exist in medium, while the latter moves due to a decrease or increase in size, and sometimes, a change in its composition. In this section, we introduce these motors in detail.

4.1 Catalytic nano/micromotors

Most catalytic nano/micromotors are propelled by consuming hydrogen peroxide as fuel, while some use hydrazine (Gao et al., 2014, Laocharoensuk et al., 2008). Because both fuels are thought to propel the motor through essentially the same mechanism, we focus solely on catalytic motors with hydrogen peroxide fuel.

In 2002, Ismagilov et al. have demonstrated a macrosized (∼1 cm) catalytic boat converting chemical into mechanical energy (Fig. 6a). At the air/water interface with hydrogen peroxide, a polymer boat with its stern covered with Pt moves for several hours. The decomposition of hydrogen peroxide,   

$$2{\text{H}}_2{\text{O}}_2\to 2{\text{H}}_2\text{O}+{\text{O}}_2,$$(4.1)

proceeds on the surface of Pt and generates a recoil force from oxygen bubbles released from the Pt surface.

Fig. 6

Examples of catalytic motors propelled by consuming hydrogen peroxide as fuel. (a) Macro motor: polymer boat with a Pt-covered stern (Ismagilov et al., 2002; copyright 2002 John Wiley & Sons, Inc., reprinted with permission), and nano/micromotors: (b) Pt/Au nanorod (Paxton et al., 2004), (c) L-shaped Si/Pt particle (Yuping et al., 2007; copyright 2007 American Chemical Society, reprinted with permission), and (d) spherical silica particle with a Pt-coated hemisphere (Gibbs and Zhao, 2009; copyright 2009 American Institute of Physics, reprinted with permission).

Two years later, Paxton et al. (2004) proposed the first synthetic nano/micromotor system (Fig. 6b). The motor system is a catalytic nanorod consisting of 1 μm-long catalytic Pt and inert Au segments immersed in a solution containing hydrogen peroxide. Around the same time, Fournier-Bidoz et al. (2005) independently demonstrated a similar nano/micromotor system using a Ni/Au rod. Very recently, Lee et al. (2014) have fabricated a quite minute Pt/Au motor with a diameter of 30 nm, which shows high ballistic speed. Interestingly, these nano/micromotors move toward the direction opposite of that in the macro motor proposed by Ismagilov et al. (2002), that is, toward the catalytic Pt or Ni end of the rod.

This unexpected motion can be explained by either interfacial tension gradient (Fig. 7a) or self-electrophoresis (Fig. 7b). In the former, the decomposition of hydrogen peroxide occurs only on the Pt surface, leading to a gradient of solute (dissolved oxygen) concentration or temperature along the rod. That is to say, the boundary layer around the Pt end has a higher oxygen concentration or temperature, which reduces interfacial tension between the solution and rod. The interfacial tension gradient causes convection flow to occur from the Pt to Au side, and the simultaneous movement of the rod toward the opposite direction according to the law of momentum conservation. Here, note that the hydrogen peroxide concentration gradient does not affect the interfacial tension of the metal/water interface because that of hydrogen peroxide water is almost identical to pure water (Phibbs and Giguere, 1951).

Fig. 7

Possible moving mechanisms of catalytic nano/micromotors. (a) Interfacial tension gradient, and (b) self-electrophoresis propel catalytic Pt motors toward the Pt side, while (c) nano/micro bubble, and (d) self-diffusiophoresis propel it away.

In the latter electrokinetic mechanism, the Pt and Au segments work as the positive and negative electrodes, respectively, causing an oxidation/reduction reaction of hydrogen peroxide as follows:   

$$\text{Pt}:\hspace{0.17em}\hspace{0.17em}{\text{H}}_2{\text{O}}_2\to {\text{O}}_2+2{\text{H}}^{+}+2{\text{e}}^{-}$$(4.2)

  

$$\text{Au}:\hspace{0.17em}\hspace{0.17em}{\text{H}}_2{\text{O}}_2+2{\text{H}}^{+}+2{\text{e}}^{-}\to 2{\text{H}}_2\text{O}$$(4.3)

The net reaction is identical to Eqn. 4.1. Hydrogen peroxide is oxidized to generate protons in solution, and electrons on the Pt side. On the other hand, protons and electrons are consumed with the reduction of hydrogen peroxide on the Au side. The resulting ion flux induces the motion of the particle relative to the fluid, propelling the particle toward the Pt end (Moran and Posner, 2011, Paxton et al., 2006, Wang et al., 2006). Self-electrophoresis seems to be more probable because the translational direction changes oppositely in the case of a composite particle of catalytic Pt and dielectric material, as will be discussed shortly.

An L-shaped Si/Pt particle immersed in hydrogen peroxide water (Fig. 6c), in contrast to bimetallic rods, moves or rotates in such a way that the rear side is catalytic Pt (Yuping et al., 2007). Likewise, spherical silica (Gibbs and Zhao, 2009), fluorescent polymer (Ebbens and Howse, 2011), or PS (Baraban et al., 2012) particles with a Pt-coating hemisphere (Fig. 6d), exhibit translational motion away from Pt. These studies imply that a composite particle of a catalytic metal and dielectric material has a different moving mechanism from a bimetallic one.

There are other possible mechanisms for the self-motion of catalytic particles, such as nano/micro bubble propulsion (Fig. 7c), and self-diffusiophoresis (Fig. 7d). Bubble propulsion seems to be a facile mechanism because the macro-sized boat proposed by Ismagilov et al. (2002) obviously moves by ejecting visible bubbles. Although no visible bubble is observed in all of the above catalytic nano/micromotor systems, nanobubbles may be created on the catalytic surface. In fact, elegant designs of a few nano/micromotor systems propelled by ejecting visible microbubbles or invisible nanobubbles have been reported (Fig. 8). Solovev et al. (2009) demonstrated that a rolled-up microtube made of a thin Pt/Au/Fe/Ti sheet moves like a rocket by bubble ejection through one opening of the tube. Furthermore, a Pt-nanoparticle-encapsulated polymer stomatocyte, which was fabricated by Wilson et al. (2012), swims through invisible nanobubble ejection through an opening. In addition, Wang and Wu (2014) demonstrated that a PS micro dimer with one lobe sprinkled with Pt nanoparticles moves through the periodic growth, and collapse of bubbles. These bubble-propelled motors commonly have a structure suitable to trap bubbles and promote its growth and coalescence, implying the possibility of bubble propulsion even if the bubbles are invisible.

Fig. 8

Catalytic nano/micromotors driven by nano/micro bubbles: (a) Rolled-up microtube made of a thin Pt/Au/Fe/Ti sheet (Solovev et al., 2009; copyright 2009 John Wiley & Sons, Inc., reprinted with permission), (b) Pt-nanoparticle-encapsulated polymer stomatocyte with an opening (Wilson et al., 2012; copyright 2012 Nature Publishing Group, reprinted with permission), and (c) PS micro dimer with one lobe sprinkled with Pt nanoparticles (Wang and Wu, 2014; copyright 2014 American Chemical Society, reprinted with permission).

Self-diffusiophoresis arises from the self-induced concentration gradient of reactants or products (Golestanian et al., 2005). In this case, the catalytic Pt surface produces oxygen continuously. As the oxygen begins to diffuse away from the catalytic surface, a steady concentration gradient of oxygen is generated as shown in Fig. 7d. This diffusion results in particle movement toward the inert side. Here, a spherical geometry is known to have a larger effect on self-diffusiophoresis than a rod-like one because velocity depends on the aspect ratio (Howse et al., 2007).

All catalytic motors introduced in this section possess compositional asymmetry, and sometimes, a complicated structure to obtain a continuous driving force and torque, which increases operational factors from the viewpoint of technology. In the next section, we discuss simpler catalytic motors made of a single metal, the motion mechanisms of which are quite different from those of the motors above.

4.2 Simpler catalytic nano/micromotors made of a single metal

Is the chemical asymmetry of a particle absolutely necessary for its regulated motion? Our answer is “No!” Perhaps literally all catalytic particles may be active in a medium containing a reactant.

A few research groups including us have investigated the motion of catalytic particles made of a single metal (Pt) instead of catalytic composites. The first catalytic monometallic motor is a Pt nanorod proposed by Kovtyukhova et al. (2008). For a monometallic motor, the critical factor to determine the motion should be its morphology. However, the rods fabricated by Kovtyukhova et al. (2008) exhibit various types of regulated motions despite the similar shape. On the other hand, we investigated the relationship between the morphology of Pt particles and dynamical modes (Yamamoto et al., 2013). We demonstrated that even a spherical catalytic Pt particle shows more vigorous random motion (active Brownian motion) in hydrogen peroxide water than the usual Brownian motion in pure water, despite the fact that non-composite particles cannot break the symmetry of the local field, that is, the net driving force is zero. However, we were able to obtain regulated motions. This suggests that a simple Pt particle causes transient asymmetry of the local field, although the mechanism of force generation (described in Sec. 4.1) is not elucidated. A stationary asymmetry induced by chemically anisotropic motors generates a constant driving force, while a transient force only generates random fluctuation. Interestingly, the resultant random fluctuation caused by the chemical reaction has a unique characteristic, a ballistic (translational) motion for a shorter time scale (< 1 s). According to the Second Law of Thermodynamics, regulated motion converts to thermal fluctuation, but not vice versa. However, a random fluctuation containing ballistic motion at a microscopic time scale can be converted to various regulated motions in appropriate situations, such as a particular morphology of the moving object or geometry of the field of particle motions. This was demonstrated in the case of aggregates of Pt particles, which exhibit various regulated motions depending on morphology as shown in Fig. 9.

Fig. 9

Summary of the authors’ research on catalytic motors made only of Pt (Yamamoto et al., 2013; copyright 2013 American Institute of Physics, reprinted with permission).

In our simple motor system, the dynamical modes (i.e., translation, rotation, and spin) of particles or aggregates depend only on their morphology. Our quantitative analysis of the two-dimensional shape can predict the dynamical mode. The analytical procedure consists of the following two steps (Fig. 10):

Fig. 10

Typical example of quantitative analysis of particle morphology (using an imaginary particle with a birdlike shape).

• [1]   First, we calculated the ratio of the axial symmetry f(ψ) of the two-dimensional shape with respect to an axis through the center of gravity, tilted at an arbitrary azimuthal angle ψ as follows:

  R(θ), which is the length between the center and edge at angle θ (−π ≤ θ ≤ π) from the ψ-axis (0 ≤ ψ ≤ π), is given as   

  $$R(\theta )=R_{\text{av}}+\delta R(\theta )$$(4.4)
  where R_av is the mean radius of a particle. Here, δR(θ) is expressed as a Fourier series   
  $$\delta R(\theta )=\sum _{n=1}^{\infty }\left(a_n\text{cos}n\theta +b_n\text{sin}n\theta \right)$$(4.5)

  The cosine term represents the axial symmetry of the particle with respect to the ψ-axis. On the other hand, the sine term, which is an odd function, represents the point symmetry. Therefore, f(ψ) (0 ≤ f ≤ 1) can be defined as   

  $$f(\psi )=\frac{\sum _{n=1}^{\infty }{a_n}^2}{\sum _{n=1}^{\infty }{a_n}^2+\sum _{n=1}^{\infty }{b_n}^2}$$(4.6)

• [2]   Among all axes (0 ≤ ψ ≤ π), the axis with the highest and lowest axial symmetry were determined and denoted as f_max and f_min, respectively. The axial symmetry-asymmetry balance (SAB) of particles was calculated as   
  $$\text{SAB}=\frac{\text{degree}\hspace{0.17em}\text{of}\hspace{0.17em}\text{symmetry}}{\text{degree}\hspace{0.17em}\text{of}\hspace{0.17em}\text{asymmetry}}=\frac{f_{\text{max}}}{1-f_{\text{min}}}$$(4.7)

From the above analysis, we found that the aggregates tend to show translational motion at SAB > 1. In addition, aggregates exhibit rotational, and spinning modes at SAB ∼ 1, and SAB < 1, respectively (Fig. 11 and Table 2). Therefore, we concluded that the motion of aggregates with various shapes could be classified based on SAB, that is, the morphological symmetry.

Fig. 11

Relationship between dynamical modes, and axial symmetry-asymmetry balance (SAB) of particles. The data correspond to those in Table 2.

Table 2 Summary of SAB values, and motion types (unpublished data)

Dynamical mode	Aggregatea	fmax[–]	1 − f min[–]	SAB [–]
Translation		0.84	0.78	1.08
		0.91	0.81	1.12
		0.95	0.90	1.06
		0.93	0.93	1.00
		0.95	0.90	1.06
		0.91	0.90	1.01
		0.89	0.90	0.99
				av. 1.04
Rotation		0.95	0.96	0.99
		0.90	0.92	0.98
		0.90	0.88	1.02
		0.90	0.89	1.01
		0.86	0.87	0.99
		0.88	0.88	1.00
		0.93	0.92	1.01
		0.95	0.92	1.03
				av. 1.00
Spin		0.92	0.97	0.95
		0.96	0.96	1.00
		0.86	0.92	0.93
		0.84	0.96	0.88
		0.94	0.95	0.99
		0.94	0.92	1.02
		0.82	0.86	0.95
		0.86	0.97	0.89
		0.84	0.89	0.94
		0.86	0.92	0.93
				av. 0.95

a  Size scale is different among all aggregates, although the range only varies from 3 to 7 μm.

Most recently, Bao et al. (2014) demonstrated that a shape-controlled catalytic motor made only of Pt moves faster than ours, although its velocity is a little slower compared with other composite motors (see Table 3).

Table 3 Summary of artificial nano/micromotors

Propulsiona	Morphologyb	Maximum velocity		Conditionc	Reference
		(μm/s)	(Body-length/s)
External field propulsion
E	Au/PS Janus particle (D: 8 μm) (see Fig. 5)	∼30	3.8	0.1 mM NaCl under an AC field (∼300 V/cm, 1 kHz)	(Gangwal et al., 2008)
M	Au/Agflex/Ni nanowire (L: ∼7 μm, D: ∼0.3 μm) (see Fig. 5)	6	0.9	Under a rotating magnetic field (5 G, 15 Hz)	(Gao et al., 2010)
M	SU-8 helical motor with Ni/Ti bilayers (L: 35 μm, D: 8.0 μm)	∼180	5.1	Under a rotating magnetic field (10 G, 60 Hz)	(Tottori et al., 2012)
U	Ru/Au or Au/Pt nanorod (L: 2 μm, D: 0.33 μm) (see Fig. 5)	200	100	Under an acoustic field (3.7 MHz)	(Wang et al., 2012)
Chemical reaction propulsion
CR (B)	Polymer boat with a Pt-covered stern (D: 9 mm, T: 1–2 mm) (see Fig. 6a) (Note that it is not a nano/micromotor!)	2 × 104	2.2	3% H2O2 water	(Ismagilov et al., 2002)
CR (SE/IT)	Pt/Au nanorod (L: 1 μm, D: 0.37 μm) (see Fig. 6b)	7.9 (14?)	7.9 (14)	3.3–5% H2O2 water	(Paxton et al., 2004).
CR (?)	Ni/Au nanorod (L: 2.5 μm, D: ∼0.2 μm)	1.5 rad/s (rotational speed)		H2O2 water (concentration: unknown)	(Fournier-Bidoz et al., 2005)
CR (SE)	Rh/Au nanorod (L: 2 μm, D: 0.37 μm)	23.8	12	5% H2O2 water	(Wang et al., 2006)
CR (SE)	Pt/(Au25–Ag75-alloy) nanorod (L: 2 μm, D: unknown)	150	75	5% H2O2 water	(Demirok et al., 2008)
CR (SE)	Pt/Au nanorod containing carbon nanotubes (L: 2 μm, D: 0.22 μm)	> 200	100	Water containing H2O2 (2.5%) and N2H4 (0.15%)	(Laocharoensuk et al., 2008)
CR (SE)	Janus-type Au particle with an embedded Pt particle on one face (D: 0.030 μm)	660 (ballistic speed)	2.2 × 104	1.5% H2O2 water	(Lee et al., 2014)
CR (SE)	Pt/PS Janus particle (D: 2 μm)	∼15	7.5	10% H2O2 water	(Brown and Poon, 2014)
CR (?)	Ni/Au nanorod with high surface area (L: 3.1 μm, D: 0.20–0.25 μm)	∼5	1.6	15% H2O2 water	(Zacharia et al., 2009)
CR (B?)	L-shaped Si/Pt nanorod (L: ∼3 μm) (see Fig. 6c)	2 rad/s (rotational speed)		5% H2O2 water	(Yuping et al., 2007)
CR (B)	Rolled-up catalytic microjet (L: 60 μm, D: 5.5 μm) (see Fig. 8a)	2000	33	15%? H2O2 water	(Solovev et al., 2009)
CR (B)	Pt/SiO2 Janus particle (D: 2 μm) (see Fig. 6d)	7.5	3.8	6% H2O2 water	(Gibbs and Zhao, 2009)
CR (B)	Pt-nanoparticle-encapsulated polymer stomatocyte with an opening (D: ∼0.15 μm) (see Fig. 8b)	∼30	200	0.3% H2O2 water	(Wilson et al., 2012)
CR (B)	PS micro dimer with one lobe sprinkled with Pt nanoparticles (L: 4 μm?) (see Fig. 8c)	∼40	10	10% H2O2 water	(Wang and Wu, 2014)
CR (SD)	Pt/Fluorescent-polymer Janus particle (D: 2 μm)	3.4	1.7	5% H2O2 water	(Ebbens and Howse, 2011)
CR (SD)	Ir/SiO2 Janus particle (D: 1.2 μm)	21	17.5	0.001% N2H4 solution	(Gao et al., 2014)
CR (SD)	Pt/PS Janus particle (D: 1.6 μm)	∼3.3	2.1	10% H2O2 water	(Howse et al., 2007)
M-CR (B)	Pt nanorod (L: 3.2 μm, D: 0.35 μm)	15	4.7	3–30% H2O2 water	(Kovtyukhova, 2008)
M-CR (SD/B?)	Streamlined Pt aggregate (L: 5 μm)	∼3	0.6	1% H2O2 water	(Yamamoto et al., 2013)
M-CR (B)	V-shaped Pt nanorobot (L: ∼5 μm, T: 0.7 μm)	∼7.3	1.5	23.6% H2O2 water	(Bao et al., 2014).
SR (SE)	Pt/Cu nanorod (L: 1 μm, D: 0.3 μm) (see Fig. 12a)	∼20	20	1.0 mM Br2	(Liu and Sen, 2011)
SR (B)	Mg particle asymmetrically coated with Ti/Ni/Au layers (D: 30 μm) (see Fig. 12b)	300	10	3 M NaCl	(Gao et al., 2013)
SR (B)	Mg/Pt Janus particle (D: 20 μm) (see Fig. 12c)	92	4.6	0.5 M NaHCO3	(Mou et al., 2013)
SR (B)	(Al-Ga-alloy)/Ti Janus particle (D: 20 μm) (see Fig. 12d)	3000	150	Ultrapure water	(Gao et al., 2012a)
SR (B)	Polyaniline/Zn microtube (L: 10 μm, D: 5 μm) (see Fig. 12e)	1050	105	Acidic water (pH: −0.2)	(Gao et al., 2012b)
For applications (chemical sensing, transport of cargo)
CR (SE)	Pt/Au nanorod (L: 2 μm, D: 0.2 μm?)	∼10 ↓ 52	5 ↓ 26	5% H2O2 water ⇒ Adding 0.1 mM AgNO3	(Kagan et al., 2009)
CR (SE)	Pt/Au/polypyrrole nanorod (L: 2.5 μm, D: 0.37 μm)	7.4 ↓ 3.9	3.0 ↓ 1.6	5% H2O2 water ⇒ With a cargo	(Sundararajan et al., 2008)
CR (SD)	Pt/PS Janus particle (D: 5 μm)	∼8.3 ↓ 5.5	1.7 ↓ 1.1	15% H2O2 water ⇒ With a cargo	(Baraban et al., 2012)
SR (B)	Mg/(Pt-NIPA) Janus particle for DDS (D: 50 μm) (see Fig. 12f)	35	0.7	Human plasma	(Mou et al., 2014)
Hybrid motor
M & CR (SE)	Pt/Au/Agflex/Ni nanowire (L: 6 μm, D: 0.2 μm)	8 (CR on) 6 (M on) 8 (M&CR on)	1.3 1.0 1.3	8% H2O2 water or pure water under/without a rotational magnetic field (10 G, 15 Hz)	(Gao et al., 2011)

a  E, M, U, CR, and SR denote electric propulsion, magnetic, ultrasound, catalytic reaction, and self-reaction, respectively. M-CR represents CR by monometallic catalytic motor. IT, SE, B, and SD shows detailed mechanisms of chemical-reaction-propelled motors, and denote interfacial tension gradient, self-electrophoresis, bubble propulsion, and self-diffusiophoresis, respectively (see Fig. 7).

b  D, L, and T denote diameter, length, and thickness, respectively.

c  The list shows the condition where motors exhibit the motion at the maximum velocity.

A simple motor is the most favorable candidate to examine the effect of shape on motion because the mode solely depends on morphology. The above-mentioned particle will give us significant insight for a sophisticated design not only for non-composite motors but also for composite ones.

4.3 Self-reacted nano/micromotors

Several research groups have attempted to fabricate self-reacted nano/micromotors. These motors move through consumption of themselves, or due to a change in composition; hence, these have limited lifetimes unlike catalytic motors. In addition, these do not require specific reactants such as hydrogen peroxide, which is incompatible with living organisms. These characteristics are preferable for biotechnological applications such as drug delivery systems (DDS) (Jain, 2008) because the motors can be dissipated by exhausting themselves after carrying drug to the destination.

To the authors’ knowledge, the first self-reacted motor is a Cu/Pt nanorod in dilute aqueous solutions of Br₂ or I₂ (Liu and Sen, 2011) (Fig. 12a). This motor is driven by self-electrophoresis, similar to the one proposed by Paxton et al. (2006). The remarkable difference is that the Cu segment, working as a negative electrode, is oxidized to Cu²⁺ (etched Cu segment in Br₂ solution) or CuI (CuI-coated Cu segment in I₂ solution).

Fig. 12

Examples of self-reacted motors. (a) Cu/Pt nanorod in dilute aqueous solutions of Br₂ or I₂ (Liu and Sen, 2011; copyright 2011 American Chemical Society, reprinted with permission), (b, c) Mg-containing Janus micromotors in seawater (Gao et al., 2013; copyright 2013 the Royal Society of Chemistry, reprinted with permission), and in water containing sodium hydrogen carbonate (Mou et al., 2013; copyright 2013 John Wiley & Sons, Inc., reprinted with permission), (d) Al-Ga alloy driven in pure water (Gao et al., 2012a; copyright 2012 American Chemical Society, reprinted with permission), (e) Zn-based microtube driven in acidic water (Gao et al., 2012b; copyright 2012 American Chemical Society, reprinted with permission), and (f) Mg-containing motor carrying, and releasing drug (Mou et al., 2014; copyright 2014 American Chemical Society, reprinted with permission).

Most of the other self-reacted nano/micromotors are those propelled by microbubbles. Mg-containing Janus micro motors are propelled by hydrogen gas generated by the oxidation of the Mg surface   

$$\text{Mg}(\text{s})+2{\text{H}}_2\text{O}\to \text{Mg}{(\text{OH})}_2(\text{s})+{\text{H}}_2.$$(4.8)

Although the resultant passivation layer of magnesium hydroxide hinders the reaction, Gao et al. (2013), and Mou et al. (2013) succeeded in sustaining it in seawater, and water-containing sodium hydrogen carbonate, respectively, through different mechanisms (Fig. 12b, c). Gao et al. also proposed other types of self-reacted motor systems, such as a Janus micro motor composed of a partially coated Al–Ga alloy driven in pure water (Gao et al., 2012a), and a Zn-based microtube driven in acidic water (Gao et al., 2012b) (Fig. 12d, e).

A quite challenging research on the application of these self-reacted motors as DDS began recently (Mou et al., 2014) (Fig. 12f). Such research will accelerate both fundamental and applied studies concerning self-reacted motors.

5. Directional control of artificial nano/micromotors

For practical uses of the above nano/micromotors, more highly functional properties, such as directional control, collective motion (Duan et al., 2013; Kagan et al., 2011), chemical sensing (Kagan et al., 2009), and transport of cargo (Sundararajan et al., 2008), are required. These characteristics are often observed in biological systems. Here, we focus on attempts at directional control of nano/micromotors.

5.1 Chemotaxis

Chemotaxis is the directional movement of an organism along a concentration gradient of chemicals (Adler, 1966). For instance, a bacterium swims toward a higher concentration of food (glucose), while it swims away from an acidic area. Chemicals that attract, and repel an organism are called a “chemoattractant,” and a “chemo-repellent,” respectively. Recently, Lagzi et al. (2010) demonstrated an interesting artificial chemotactic system, namely “maze solving by chemotactic droplet.” At the water/air interface, a millimeter-sized oil droplet moved from the entrance to the goal of the maze (Fig. 13a). This chemotaxis can be explained as follows. First, an acid-soaked gel is placed at the goal to form a pH gradient. Then, a droplet containing surfactants is put at the entrance. Because of the interfacial tension gradient depending on the pH of the surfactant system, the droplet shows chemotactic motion toward the chemoattractant (the acid-soaked gel).

Fig. 13

Chemotaxis of artificial objects. (a) Millimeter-sized oil droplet moving from the entrance to the goal of the maze (Lagzi et al., 2010; copyright 2010 American Chemical Society, reprinted with permission), and (b) collective motion of Pt/Au nanorods toward an agar gel containing 30% hydrogen peroxide water (Hong et al., 2007, Sen et al., 2009; copyright 2009 The Royal Society of Chemistry, reprinted with permission).

The first example of chemotaxis with nano/micromotors in a laboratory was demonstrated by Hong et al. (2007). When Pt/Au rods were put under a concentration gradient of hydrogen peroxide, which is generated by an agar gel containing 30% hydrogen peroxide, these gathered in the vicinity of the gel (Fig. 13b). This is because the active diffusion constant of the rods became larger with an increase in the concentration of the reactant. Furthermore, Baraban et al. (2013) demonstrated that catalytic motors with different morphologies, a tubular microjet and Janus particle, also show chemotactic behavior in microfluidic channels. Although the chemotactic motion demonstrated by Hong et al. (2007) takes a long time (almost 30% and 70% of the rods were accumulated at the gel after 38 h and 110 h, respectively), these motors show collective motion toward the chemoattractant. This is quite interesting and promising, not only for biomimetic technology, but also for reaction technology with catalysts.

5.2 Control with external field and confined space

As mentioned in Sec. 2.3, thermal fluctuation converts the directional motion of nano/micromotors into active Brownian motion at a macroscopic scale. Directional control of nano/micromotors driven by chemical reactions has been attempted mainly under a magnetic field, for instance, by Kline et al. (2005) with Pt/Ni/Au/Ni/Au rods (Fig. 14a). Without the magnetic field, the rods exhibit translational motion in hydrogen peroxide water with a high rotational diffusion constant (0.2 rad² s⁻¹). On the other hand, an applied magnetic field aligns the rods along a direction perpendicular to the field (0.02 rad² s⁻¹). Note that the field serves to orient the rods and does not affect the motion itself. Furthermore, a catalytic Ni-containing microtube and microrod propelled by microbubbles also show complicated motions such as stop, turn, and go, depending on the magnetic field vector (Burdick et al., 2008; Zhao and Pumera, 2012).

Fig. 14

Directional control with external field and confined space. (a) Pt/Ni/Au/Ni/Au rod motion under a magnetic field (Kline et al., 2005; copyright 2005 John Wiley & Sons, Inc., reprinted with permission), and directional motion of Pt particles along a microchannel, with trajectory and snapshots of motion shown in (b1), and corresponding spatiotemporal diagram of motion on a vertical line along the microchannel shown in (b2) (unpublished data).

The authors’ group is now trying to fabricate a micro motor system that mimics motor proteins, which exhibits directional and sustainable motion along a monorail. Our strategy is to control the motion of a catalytic Pt particle using a microchannel. Fig. 14b shows our preliminary data for Pt particle motion in a microchannel, with several micrometers in width and depth in hydrogen peroxide water. The particle exhibits directed motion along the channel without rotations, which resembles a molecular motor walking along a microtubule. Although fluctuations cause random noise in the motion, the particle can exhibit an almost linear motion with constant velocity. This result may be applied to microdevices such as the microcarrier system shown in Fig. 2.

6. Summary and Conclusions

In this article, we reviewed artificial nano/micromotors, which are summarized in Table 3. First of all, we discussed the underlying physics of nano/micromotors (Sec. 2). The key terms for the motion of nano/micro objects are “ultralow Reynolds number,” and “thermal fluctuation.” The former means that viscous force dominates the motion instead of inertia. Therefore, the motion of nano/micro objects reaches terminal regulated motion or turns into Brownian motion immediately after the driving force works or ceases, respectively. The latter converts regulated motion to active Brownian motion at a macroscopic time scale. Because the rotational diffusion constant D_R of an object increases with a decrease in size (D_R ∝ d_p⁻³ for a spherical particle with diameter d_p), it is difficult for smaller particles to maintain its regulated motion for a long period.

To overcome these effects of viscous drag and thermal fluctuation, artificial nano/micromotors propelled by various mechanisms, such as chemical reaction, electric, magnetic, and ultrasound propulsion, have been proposed in the last decade as explained in Sec. 3. Most possess compositional asymmetry to gain the continuous anisotropic driving force or torque required for motion. Furthermore, a hybrid nano/micromotor driven by two different mechanisms, namely magnetic and chemical reaction propulsions, has been studied recently, although both propulsions do not accelerate the translational velocity dramatically as shown in Table 3 (Gao et al., 2011).

In Sec. 4, we focused on motors driven by chemical reactions because chemical reactions are one of the most familiar phenomena for chemical engineers, especially those who are engaged in powder technology, and because numerous biomotors are driven by chemical reactions. Such reaction-driven motors are classified into catalytic and self-reacted ones. Although some catalytic motors are similarly driven by the decomposition of hydrogen peroxide, the driving forces can arise from various mechanisms, such as interfacial tension gradient, self-electrophoresis, nano/micro bubbles, and self-diffusiophoresis. The self-reacted ones have a limited lifetime, and a few move by decreasing in size, which is preferable for biotechnological applications such as DDS. We feel that there are few reactions that produce the driving force required for the two types of reaction-propelled motors mentioned above. If the above-mentioned “active motion” could be observed for other types of chemical reactions, such as catalytic or solid-state reactions, this novel transport phenomenon would have a remarkable impact on chemical systems proposed by chemical engineers.

In Sec. 5, we introduced some examples of directional control of artificial nano/micromotors for possible applications. In particular, the chemotaxis of a catalytic motor can enhance its catalytic activity, not by catalyst chemistry, but by its mobility.

In conclusion, we expect that non-equilibrium phenomena including “active motion” can be applied to chemical systems in the future. This is because systems adopting such phenomena, which are ubiquitous in nature, can accomplish more functional or efficient work. The “active motion” of nano/micro objects is often observed in our bodies, meaning that all organisms are “natural” chemical engineers! Therefore, control of an artificial nano/micromotor seems to be attainable, although there is still a long way to go toward its realization. Because such a non-equilibrium phenomenon sometimes produces chaos, strict control of the motor may be difficult. Now is just the time for us, “learned” chemical engineers, to show our skills in process design and control. If we can drive a runaway motor vehicle, the unknown world spreads out before us!

Acknowledgements

Our research on the active motion of Pt catalytic particles was supported in part by Hosokawa Powder Technology Foundation, and by Grant-in-Aid for Young Scientists (B) (Grant No. 26820341 23656497) from the Japan Society for the Promotion of Science (JSPS).

Author’s short biography

Daigo Yamamoto

Dr. Daigo Yamamoto graduated from Kyoto University in 2006, and the graduate school of the same university in 2008. He received a Ph.D. in Engineering from Kyoto University under the supervision of Prof. Minoru Miyahara in 2011. Then, he worked as a research fellow in the laboratory of Prof. Kazuhiro Mae for a year, where his research focused on the synthesis of nanoparticles with nano/micro reaction fields using a dendrimer, and micro-mixer. He is currently an assistant professor at Doshisha University, and is involved in non-equilibrium phenomena such as spontaneous motion, and self-assembly.

Akihisa Shioi

Dr. Akihisa Shioi, a professor of chemical engineering, and materials science at Doshisha University, has been focusing his research on the dynamics, and pattern formation of non-equilibrium chemical systems. His research interests are the development of chemical systems that mimic the behavior of living matter, and the determination of characteristics that impart a semblance of life to chemical systems.

References

•  Adler  J., Chemotaxis in bacteria, Science, 153 (1966) 708–716.
•  Adler  J.,  Tso  W.W., “Decision”-making in bacteria: Chemotactic response of escherichia coli to conflicting stimuli, Science, 184 (1974) 1292–1294.
•  Anderson  P.W., More is different, Science, 177 (1972) 393–396.
•  Bainbridge  R., The speed of swimming of fish as related to size and to the frequency and amplitude of the tail beat, Journal of Experimental Biology, 35 (1958) 109–133.
•  Bao  J.,  Yang  Z.,  Nakajima  M.,  Shen  Y.,  Takeuchi  M.,  Huang  Q.,  Fukuda  T., Self-actuating asymmetric platinum catalytic mobile nanorobot, IEEE Transactions on Robotics, 30 (2014) 33–39.
•  Baraban  L.,  Harazim  S.M.,  Sanchez  S.,  Schmidt  O.G., Chemotactic behavior of catalytic motors in microfluidic channels, Angewandte Chemie International Edition, 52 (2013) 5552–5556.
•  Baraban  L.,  Tasinkevych  M.,  Popescu  M.N.,  Sanchez  S.,  Dietrich  S.,  Schmidt  O.G., Transport of cargo by catalytic Janus micro-motors, Soft Matter, 8 (2012) 48–52.
•  Berg  H.C.,  Anderson  R.A., Bacteria swim by rotating their flagellar filaments, Nature, 245 (1973) 380–382.
•  Bird  R.B.,  Stewart  W.E.,  Lightfoot  E.N., Transport phenomena, Wiley, New Jersey, 2007.
•  Blaustein  M.P.,  Lederer  W.J., Sodium/calcium exchange: Its physiological implications, Physiological Reviews, 79 (1999) 763–854.
•  Brown  A.,  Poon  W., Ionic effects in self-propelled Pt-coated Janus swimmers, Soft Matter, 10 (2014) 4016–4027.
•  Burdick  J.,  Laocharoensuk  R.,  Wheat  P.M.,  Posner  J.D.,  Wang  J., Synthetic nanomotors in microchannel networks: Directional microchip motion and controlled manipulation of cargo, Journal of the American Chemical Society, 130 (2008) 8164–8165.
•  Campuzano  S.,  Kagan  D.,  Orozco  J.,  Wang  J., Motion-driven sensing and biosensing using electrochemically propelled nanomotors, Analyst, 136 (2011) 4621–4630.
•  Cussler  E.L., Diffusion: Mass transfer in fluid systems, Cambridge University Press, Cambidge, 2009.
•  Demirok  U.K.,  Laocharoensuk  R.,  Manesh  K.M.,  Wang  J., Ultrafast catalytic alloy nanomotors, Angewandte Chemie International Edition, 47 (2008) 9349–9351.
•  Duan  W.,  Liu  R.,  Sen  A., Transition between collective behaviors of micromotors in response to different stimuli, Journal of the American Chemical Society, 135 (2013) 1280–1283.
•  Dueck  J., The sedimentation velocity of a particle in a wide range of Reynolds numbers in the application to the analysis of the separation curve, Advanced Powder Technology, 24 (2013) 150–153.
•  Ebbens  S.J.,  Howse  J.R., Direct observation of the direction of motion for spherical catalytic swimmers, Langmuir, 27 (2011) 12293–12296.
•  Einstein  A., Über die von der molekularkinetischen theorie der wärme geforderte bewegung von in ruhenden flüssigkeiten suspendierten teilchen, Annalen der Physik, 322 (1905) 549–560.
•  Fenteany  G.,  Glogauer  M., Cytoskeletal remodeling in leukocyte function, Current Opinion in Hematology, 11 (2004) 15–24.
•  Fournier-Bidoz  S.,  Arsenault  A.C.,  Manners  I.,  Ozin  G.A., Synthetic self-propelled nanorotors, Chemical Communications, (2005) 441–443.
•  Gangwal  S.,  Cayre  O.J.,  Bazant  M.Z.,  Velev  O.D., Induced-charge electrophoresis of metallodielectric particles, Physical Review Letters, 100 (2008) 058302.
•  Gao  W.,  Feng  X.,  Pei  A.,  Gu  Y.,  Li  J.,  Wang  J., Seawater-driven magnesium based Janus micromotors for environmental remediation, Nanoscale, 5 (2013) 4696–4700.
•  Gao  W.,  Manesh  K.M.,  Hua  J.,  Sattayasamitsathit  S.,  Wang  J., Hybrid nanomotor: A catalytically/magnetically powered adaptive nanowire swimmer, Small, 7 (2011) 2047–2051.
•  Gao  W.,  Pei  A.,  Dong  R.,  Wang  J., Catalytic iridium-based Janus micromotors powered by ultralow levels of chemical fuels, Journal of the American Chemical Society, 136 (2014) 2276–2279.
•  Gao  W.,  Pei  A.,  Wang  J., Water-driven micromotors, ACS Nano, 6 (2012a) 8432–8438.
•  Gao  W.,  Sattayasamitsathit  S.,  Manesh  K.M.,  Weihs  D.,  Wang  J., Magnetically powered flexible metal nanowire motors, Journal of the American Chemical Society, 132 (2010) 14403–14405.
•  Gao  W.,  Uygun  A.,  Wang  J., Hydrogen-bubble-propelled zinc-based microrockets in strongly acidic media, Journal of the American Chemical Society, 134 (2012b) 897–900.
•  Garland  T., The relation between maximal running speed and body mass in terrestrial mammals, Journal of Zoology, 199 (1983) 157–170.
•  Gibbs  J.G.,  Zhao  Y.P., Autonomously motile catalytic nanomotors by bubble propulsion, Applied Physics Letters, 94 (2009) 163104.
•  Golestanian  R.,  Liverpool  T.B.,  Ajdari  A., Propulsion of a molecular machine by asymmetric distribution of reaction products, Physical Review Letters, 94 (2005) 220801.
•  Hong  Y.,  Blackman  N.M.K.,  Kopp  N.D.,  Sen  A.,  Velegol  D., Chemotaxis of nonbiological colloidal rods, Physical Review Letters, 99 (2007) 178103.
•  Horsthemke  W., Noise induced transitions, in:  Vidal  C.,  Pacault  A. (Eds), Non-equilibrium dynamics in chemical systems, Springer Berlin Heidelberg, 1984, pp. 150–160.
•  Howse  J.R.,  Jones  R.a.L.,  Ryan  A.J.,  Gough  T.,  Vafabakhsh  R.,  Golestanian  R., Self-motile colloidal particles: From directed propulsion to random walk, Physical Review Letters, 99 (2007) 048102.
•  Ismagilov  R.F.,  Schwartz  A.,  Bowden  N.,  Whitesides  G.M., Autonomous movement and self-assembly, Angewandte Chemie International Edition, 41 (2002) 652–654.
•  Jain  K.K., Drug delivery systems, Humana Press, New York City, 2008.
•  Kagan  D.,  Balasubramanian  S.,  Wang  J., Chemically triggered swarming of gold microparticles, Angewandte Chemie International Edition, 50 (2011) 503–506.
•  Kagan  D.,  Calvo-Marzal  P.,  Balasubramanian  S.,  Sattayasamitsathit  S.,  Manesh  K.M.,  Flechsig  G.U.,  Wang  J., Chemical sensing based on catalytic nanomotors: Motion-based detection of trace silver, Journal of the American Chemical Society, 131 (2009) 12082–12083.
•  Kanai  Y.,  Dohmae  N.,  Hirokawa  N., Kinesin transports RNA: Isolation and characterization of an RNA-transporting granule, Neuron, 43 (2004) 513–525.
•  Kline  T.R.,  Paxton  W.F.,  Mallouk  T.E.,  Sen  A., Catalytic nanomotors: Remote-controlled autonomous movement of striped metallic nanorods, Angewandte Chemie International Edition, 44 (2005) 744–746.
•  Kovtyukhova  N.I., Toward understanding of the propulsion mechanism of rod-shaped nanoparticles that catalyze gas-generating reactions, The Journal of Physical Chemistry C, 112 (2008) 6049–6056.
•  Lagzi  I.,  Soh  S.,  Wesson  P.J.,  Browne  K.P.,  Grzybowski  B.A., Maze solving by chemotactic droplets, Journal of the American Chemical Society, 132 (2010) 1198–1199.
•  Laocharoensuk  R.,  Burdick  J.,  Wang  J., Carbon-nanotube-induced acceleration of catalytic nanomotors, ACS Nano, 2 (2008) 1069–1075.
•  Lee  T.C.,  Alarcón-Correa  M.,  Miksch  C.,  Hahn  K.,  Gibbs  J.G.,  Fischer  P., Self-propelling nanomotors in the presence of strong Brownian forces, Nano Letters, 14 (2014) 2407–2412.
•  Lim  J.,  Lanni  C.,  Evarts  E.R.,  Lanni  F.,  Tilton  R.D.,  Majetich  S.A., Magnetophoresis of nanoparticles, ACS Nano, 5 (2011) 217–226.
•  Liu  R.,  Sen  A., Autonomous nanomotor based on copper-platinum segmented nanobattery, Journal of the American Chemical Society, 133 (2011) 20064–20067.
•  Moran  J.L.,  Posner  J.D., Electrokinetic locomotion due to reaction-induced charge auto-electrophoresis, Journal of Fluid Mechanics, 680 (2011) 31–66.
•  Mou  F.,  Chen  C.,  Ma  H.,  Yin  Y.,  Wu  Q.,  Guan  J., Self-propelled micromotors driven by the magnesium–water reaction and their hemolytic properties, Angewandte Chemie International Edition, 52 (2013) 7208–7212.
•  Mou  F.,  Chen  C.,  Zhong  Q.,  Yin  Y.,  Ma  H.,  Guan  J., Autonomous motion and temperature-controlled drug delivery of Mg/Pt-poly(N-isopropylacrylamide) Janus micromotors driven by simulated body fluid and blood plasma, ACS Applied Materials & Interfaces, 6 (2014) 9897–9903, 10.1021/am502729y (2014).
•  Paxton  W.F.,  Baker  P.T.,  Kline  T.R.,  Wang  Y.,  Mallouk  T.E.,  Sen  A., Catalytically induced electrokinetics for motors and micropumps, Journal of the American Chemical Society, 128 (2006) 14881–14888.
•  Paxton  W.F.,  Kistler  K.C.,  Olmeda  C.C.,  Sen  A.,  St. Angelo  S.K.,  Cao  Y.,  Mallouk  T.E.,  Lammert  P.E.,  Crespi  V.H., Catalytic nanomotors: Autonomous movement of striped nanorods, Journal of the American Chemical Society, 126 (2004) 13424–13431.
•  Phibbs  M.K.,  Giguere  P.A., Hydrogen peroxide and its analogues. I. Density, refractive index, viscosity, and surface tension of deuterium peroxide-deuterium oxide solutions, Canadian journal of chemistry, 29 (1951) 173–181.
•  Phillips  R.B.,  Kondev  J.,  Theriot  J., Physical biology of the cell, Taylor & Francis Group, 2009.
•  Romanczuk  P., Active motion and swarming: From individual to collective dynamics, Logos Verlag Berlin, Berlin, 2011.
•  Schlichting  H., Boundary layer theory, Mac Graw-Hill, New York, 1955.
•  Sen  A.,  Ibele  M.,  Hong  Y.,  Velegol  D., Chemo and phototactic nano/microbots, Faraday Discussions, 143 (2009) 15–27.
•  Solovev  A.A.,  Mei  Y.,  Ureña  E.B.,  Huang  G.,  Schmidt  O.G., Catalytic microtubular jet engines self-propelled by accumulated gas bubbles, Small, 5 (2009) 1688–1692.
•  Strogatz  S.H., Nonlinear dynamics and chaos: With applications to physics, biology, chemistry, and engineering, Westview Press, Colorado, 1994.
•  Sundararajan  S.,  Lammert  P.E.,  Zudans  A.W.,  Crespi  V.H.,  Sen  A., Catalytic motors for transport of colloidal cargo, Nano Letters, 8 (2008) 1271–1276.
•  Suwa  M.,  Watarai  H., Magnetoanalysis of micro/nanoparticles: A review, Analytica Chimica Acta, 690 (2011) 137–147.
•  Svarovsky  L., Solid-liquid separation. Second edition, Butterworth, Oxford, 1981.
•  Takinoue  M.,  Atsumi  Y.,  Yoshikawa  K., Rotary motion driven by a direct current electric field, Applied Physics Letters, 96 (2010) 104105.
•  Ten Hagen  B.,  Van Teeffelen  S.,  Löwen  H., Brownian motion of a self-propelled particle, Journal of Physics Condensed Matter, 23 (2011) 194119.
•  Tennekes  H., The simple science of flight: From insects to jumbo jets, MIT Press, Massachusetts, 1997.
•  Tottori  S.,  Zhang  L.,  Qiu  F.,  Krawczyk  K.K.,  Franco-Obregõn  A.,  Nelson  B.J., Magnetic helical micromachines: Fabrication, controlled swimming, and cargo transport, Adv. Mater., 24 (2012) 811–816.
•  Uhlenbeck  G.E.,  Ornstein  L.S., On the theory of the Brownian motion, Physical Review, 36 (1930) 823–841.
•  Vale  R.D.,  Funatsu  T.,  Pierce  D.W.,  Romberg  L.,  Harada  Y.,  Yanagida  T., Direct observation of single kinesin molecules moving along microtubules, Nature, 380 (1996) 451–453.
•  Vale  R.D.,  Milligan  R.A., The way things move: Looking under the hood of molecular motor proteins, Science, 288 (2000) 88.
•  Van Den Heuvel  M.G.L.,  Dekker  C., Motor proteins at work for nanotechnology, Science, 317 (2007) 333–336.
•  Vogel  S., Life in moving fluids: The physical biology of flow, Princeton University Press, New Jersey, 1994.
•  Von Smoluchowski  M., Zur kinetischen theorie der Brownschen molekularbewegung und der suspensionen, Annalen der Physik, 326 (1906) 756–780.
•  Wang  S.,  Wu  N., Selecting the swimming mechanisms of colloidal particles: Bubble propulsion versus self-diffusiophoresis, Langmuir, 30 (2014) 3477–3486.
•  Wang  W.,  Castro  L.A.,  Hoyos  M.,  Mallouk  T.E., Autonomous motion of metallic microrods propelled by ultrasound, ACS Nano, 6 (2012) 6122–6132.
•  Wang  W.,  Duan  W.,  Ahmed  S.,  Mallouk  T.E.,  Sen  A., Small power: Autonomous nano- and micromotors propelled by self-generated gradients, Nano Today, 8 (2013) 531–554.
•  Wang  Y.,  Hernandez  R.M.,  Bartlett  Jr D.J.,  Bingham  J.M.,  Kline  T.R.,  Sen  A.,  Mallouk  T.E., Bipolar electrochemical mechanism for the propulsion of catalytic nanomotors in hydrogen peroxide solutions, Langmuir, 22 (2006) 10451–10456.
•  Westermeier  R., Electrophoresis in practice, Wiley, New Jersey, 2006.
•  Wilson  D.A.,  Nolte  R.J.M.,  Van Hest  J.C.M., Autonomous movement of platinum-loaded stomatocytes, Nature Chemistry, 4 (2012) 268–274.
•  Yamamoto  D.,  Mukai  A.,  Okita  N.,  Yoshikawa  K.,  Shioi  A., Catalytic micromotor generating self-propelled regular motion through random fluctuation, Journal of Chemical Physics, 139 (2013) 034705.
•  Yuping  H.,  Jinsong  W.,  Yiping  Z., Designing catalytic nanomotors by dynamic shadowing growth, Nano Letters, 7 (2007) 1369–1375.
•  Zacharia  N.S.,  Sadeq  Z.S.,  Ozin  G.A., Enhanced speed of bimetallic nanorod motors by surface roughening, Chemical Communications, (2009) 5856–5858.
•  Zhang  L.,  Peyer  K.E.,  Nelson  B.J., Artificial bacterial flagella for micromanipulation, Lab on a Chip—Miniaturisation for Chemistry and Biology, 10 (2010) 2203–2215.
•  Zhao  G.,  Pumera  M., Magnetotactic artificial self-propelled nanojets, Langmuir, 29 (2012) 7411–7415.