Modeling of Magnetic-Field-Assisted Fluidization: Model Development and CFD Simulation of Magnetically Stabilized Fluidized Beds

Abstract

Magnetic-field-assisted fluidization is starting to be considered as a viable alternative to standard fluidized beds for those operations (such as particle separations, filtration, adsorption) in which the solid phase can be made of magnetic particles or, alternatively, the fluidizing agent is a ferro-fluid; thus the fluid bed responds to the action of magnetic fields, and stabilized fluidization regimes can be generated.

One of the major difficulties to be tackled is the development of a predictive model capable of estimating the stabilized-to-bubbling transition velocity for a given magnetic field or, on the other hand, the magnetic field intensity required to stabilize the bed to a quiescent condition. The fluid dynamics prediction of a stabilized bed is also a challenging task at the moment.

On this basis, a very simple model for the description of MSFB was derived in this contribution starting from basic fluid dynamics and magnetodynamics equations. The model was implemented in a commercial CFD code in order to simulate the effect of the magnetic field onset on a freely bubbling fluidized bed.

1. Introduction

Magnetic-field-assisted fluidization (MFAF) is a technology that, in the last decades, has started to be considered as a possible alternative to standard fluidized beds for those operations in which magnetic particles or ferro-fluids can be employed. The Magnetic Stabilized Fluidized Bed Reactor (MSFBR, or simply MSFB) is a fluidized bed in which the solid phase is composed of magnetic particles or, alternatively, the fluidizing agent is a ferro-fluid; the whole system is surrounded by an array of coils that generates a magnetic, usually axial, field.

A large number of applications for MSFBs have been proposed in the past. The main fields in which the MSFB has been applied includes particle separations, filtration, fluidized bed reactors, fluidized bed adsorption, biochemical applications, fluid bed chromatography. In fact, in its simplest form, the magnetic field action eliminates gas bubbling from a fluidized bed (i.e. magnetically ‘stabilizes’), giving rise to smooth fluidization at higher gas flow rates than those achievable in the non-stabilized bed. An MSFB has the primary advantage of combining the low pressure drop of a fluidized bed with the bubble-free operation of a fixed bed (Rosensweig, 1978; Saxena and Shrivastava, 1991; Webb et al., 1996).

A systematization of the operating modes of MFAF has been done by Hristov (2002). The fluid flow and the magnetic field can be applied independently, hence two principal magnetization modes are possible: magnetization FIRST and magnetization LAST.

The term magnetization FIRST was introduced by Siegell (1987). This mode implies the application of the magnetic field on the fixed bed with an isotropic structure and static particle arrangement and the fluidization afterwards (Kirko and Filippov, 1960; Rosensweig, 1979; Hristov, 2002). In this case inter-particle forces play an important role. As a result of particle magnetization, the cohesive force of magnetic nature emerges. After the magnetic field application, an increase in flow rate gives rise to a deformation of the initial static bed with simultaneous orientation of particles along the field, leading to the so-called stabilized bed as suggested by Rosensweig (1979). The bed appears like a fixed bed with anisotropic particle arrangement induced by field lines. This state has been considered as a transitional state between fixed bed and fluidization or as homogeneous fluidization without bubbles. Further increase of the flow rate leads to fluidization of the particle aggregates and then the formation of bubbles, with the hydrodynamic forces progressively overcoming the magnetic forces until eventually particle aggregates are destroyed and fully bubbling fluidization occurs.

In magnetization LAST mode, the magnetic field is applied to a fully fluidized bed. The magnetic force causes the particles to reduce their motion and form aggregates which are aligned along field lines. At high field intensity, the bed will ultimately collapse resulting in a fixed anisotropic structure of particle aggregates. As in the previous case, the regime of homogeneous fluidization of strings is observed.

Experimental investigation in magnetization LAST is scarce compared to magnetization FIRST. Hristov and Ivanova (1999) performed different experimental tests, obtaining similar regimes to those obtained in magnetization FIRST mode. In magnetization LAST mode, a similar sequence of fluidization regimes is observed, increasing the magnetic field intensity for a given value of the fluid velocity.

However, even if the technique of MSFBs is almost 40 years old, it has not been applied yet on a large scale. One of the main problems is the choice of a suitable magnetic system. Another one is the ability of predicting with acceptable accuracy the behavior of the full-scale equipment.

The recent development of mathematical modeling of particulate solids behavior, together with the increased computing power, enables researchers to simulate the behavior of fluidized powders (with and without applied magnetic fields) and to link fundamental particle properties directly to the powder behavior. In this regard, computational fluid dynamics (CFD) modeling provides a fundamental tool to support engineering design and research in multiphase systems. In general, many authors recognize that computational modeling in multiphase systems has the potential to increase process efficiency and reduce the number of scale-up steps in the design of reliable commercial plants.

Among the many aspects of research in this field, there is a substantial interest in trying to develop a model capable of estimating the regime transitions occurring in the MSFB, as well as to correctly simulate the fluid dynamics of the bed itself.

2. Literature review

Mathematical modeling of fluidized beds can be regarded as a multiphase flow problem. In a fluid bed, solid particles are suspended in a fluid, the former having a discrete nature while the latter is considered a continuum. Thus, fluidization is described as a dispersed particulate two-phase flow. The great variety of different flow regimes in fluidization (Kunii and Levenspiel, 1991; Geldart, 1973) outlines the complexity of multiphase flow. This in turn implies a major difficulty for the general formulation of governing equations. Complete descriptions of Eulerian-Eulerian models derivation and additional information can be found in Ishii (1975), Anderson and Jackson (1967) and Jackson (2001). The Eulerian-Eulerian modeling approach can be extended to the mathematical modeling of magneto-fluidized beds. This implies the inclusion of additional magnetic body forces in the momentum balance equations, which have to be coupled with Maxwell’s magneto-static equations. This can be done within the framework of existing models. However, two very important aspects have to be noted: the Eulerian-Eulerian approach considers the solid phase as a continuum fluid, hence magnetic inter-particle force and magnetic torque cannot be directly considered, hence these models cannot predict typical phenomena of MSFBs such as the formation of strings and aggregates at high field intensities. However, the relevant macroscopic effects can in principle be accounted for, ultimately allowing the simulation of large-scale units.

Conversely, in order to simulate these phenomena, Eulerian-Lagrangian approaches would be required, able to directly account for the strong inter-particle forces, intense local polarization and complex structures deriving from intense magnetic field action (Rosensweig and Ciprios, 1991).

The first rigorous mathematical description of fluidization in the presence of a magnetic field was proposed by Rosensweig (1985). The model developed by Rosensweig is based on that proposed by Anderson and Jackson (1967). The latter follows a semi-fundamental approach based on the definitions of space average quantities on a volume which respects the scale separation condition. Rosensweig extends the analysis of Anderson and Jackson by also applying the averaging procedure to the magneto-static equations. Another model for the description of magneto-fluidized beds was developed by Brandani and Astarita (1996). The model is based on Foscolo and Gibilaro’s Particle Bed Model (Foscolo and Gibilaro, 1987), which has proved to give qualitative and quantitative agreement with experimental results. In this new model, magnetic forces acting on particles are included in the one-dimensional equations of change of Foscolo and Gibilaro.

Within the field of magneto-stabilized fluidized beds (MSFB), very few contributions in the pertinent literature dealt with the CFD simulation of this class of equipment: Li et al. (2010) simulated the flow behavior of gas and solids in a two-dimensional magnetically assisted bubbling fluidized bed with magnetic balls under a vertical-gradient magnetic field. In this case, the motion of the gas was simulated by computational fluid dynamics (CFD), while the particles were simulated using the discrete element method (DEM), thus allowing for the simulation of particle chain formation; thanks to DEM modeling it is also possible to assess the decrease of particle diffusion coefficient with the increase of magnetic field intensity.

The classic multi-fluid modeling approach was also used in the relevant literature: even if some phenomena can only be partially simulated (at most, their macroscopic effect), the relative computational easiness allows the simulation of large-scale equipment. Wang et al. (2002) carried out a numerical simulation (based on Two Fluid Model and Kinetic Theory of Granular Flow) and relevant experimental validation of a cylindrical magneto-fluidized bed. The numerical results indicated that below nil or a weak magnetic field, the typical bubbling fluidization was obtained, while under a moderate magnetic field, the particles display stable fluidization by restraining bubble formation. The numerical results were found to be in agreement with the experimental data, reflecting the ability of CFD codes to tackle the simulation problem. Xu and Guan (2003) simulated an Air-Dense Medium Fluidized Bed in which a magnetic medium was used in order to further stabilize the fluidized bed and increase the equipment efficiency.

In the present work, a first attempt to develop and implement a simple mathematical model in a commercial CFD code has been made in order to perform 2-dimensional simulations of a magnetically stabilized fluidized bed. The commercial CFD code CFX 4.4 was adopted, which allows substantial flexibility in including additional terms in the momentum balance equation.

3. Mathematical model

In this section, the mathematical model to be used for the CFD simulation of magneto-fluidized beds is presented. This model is an extension of the fluidization model proposed by Brandani and Zhang (2006).

In general, the basic equations describing the momentum balance in a fluidized bed are usually in a symmetric form and always include a term for drag force, for gravity force and for the pressure gradient. However, this formulation is unable to predict the existence (experimentally observed) of the regime of homogeneous fluidization, so the model has to be suitably extended (by means of additional terms) in order to be able to predict the transition between homogeneous and bubbling fluidization.

In general, three types of additional forces can be added: fluid-particle interactions (other than the normal drag force), particle-particle interactions, and forces resulting from the averaging procedure to obtain continuum formulation. In any case, these additional terms lead to an elasticity of the bed or particle pressure which allows the existence of stable, smooth fluidization.

In the Particle Bed Model by Foscolo and Gibilaro (1987), subsequently revised in Gibilaro (2001), a fluid-particle force term is added to the solid momentum balance. However, in accordance to Newton’s third law, a force arising from fluid-particle interactions should cancel out over summation and not be present in the overall momentum balance. In the model by Brandani and Zhang (2006), the discretized momentum balance equations are formulated in such a way that if a term is added to the particle-phase equation, a similar term appears also in the fluid-phase equation.

The basic relationships proposed by the authors are assumed as the basis for the present work. In this contribution, the momentum balance equations are extended here with the addition of a magnetic force term:   

$$\begin{array}{ll}\varphi {\rho }_{\text{p}}\left(\frac{\partial u_{\text{p}}}{\partial t}+u_{\text{p}}\frac{\partial u_{\text{p}}}{\partial z}\right)=\hfill & F_{\text{D}}-(E_{\text{mp}}+E_{\text{p}})\frac{\partial \varphi }{\partial z}\hfill \\ \hfill & -\varphi \left({\rho }_{\text{p}}g+\frac{\partial P}{\partial z}\right)\hfill \end{array}$$(1)

  

$$\begin{array}{ll}\varepsilon {\rho }_{\text{f}}\left(\frac{\partial u_{\text{f}}}{\partial t}+u_{\text{f}}\frac{\partial u_{\text{f}}}{\partial z}\right)=\hfill & -F_{\text{D}}-(E_{\text{mf}}+E_{\text{f}})\frac{\partial \varepsilon }{\partial z}\hfill \\ \hfill & -\varepsilon \left({\rho }_{\text{f}}g+\frac{\partial P}{\partial z}\right)\hfill \end{array}$$(2)

  

$$E_{\text{p}}=\delta g\left[(1-2\varphi ){\rho }_{\text{f}}+2\varphi {\rho }_{\text{p}}\right]$$(3)

  

$$E_{\text{f}}=\delta g\left[(1-2\varepsilon ){\rho }_{\text{p}}+2\varepsilon {\rho }_{\text{f}}\right]$$(4)

Notably, the momentum balance equations include the usual drag force term (F_D), and two additional elastic terms (dependent on the volume fraction gradient) appear for each phase: the fluid dynamic elasticity (E_p, E_f) as derived by Brandani and Zhang (2006), and the magnetic force terms (E_mp, E_mf). The factor δ that appears in the last two equations is a characteristic length of the order of the particle’s diameter which arises from the formulation of a discretized balance. These equations are obtained without any simplifying assumption except for neglecting higher-order terms when shifting from the discrete form to the differential form (Brandani and Zhang, 2006).

A more complex problem is that of calculation of the additional body forces due to the magnetic field. The basic relations linking the magnetic field, H, the induction field, B₀, and the magnetization, M, are:   

$$M=\varepsilon M_{\text{f}}+\varphi M_{\text{p}}=\varepsilon {\chi }_{\text{f}}{H}_{\text{f}}+\varphi {\chi }_{\text{p}}{H}_{\text{p}}$$(5)

  

$$H=\varepsilon H_{\text{f}}+\varphi H_{\text{p}}$$(6)

  

$$M=\chi H$$(7)

  

$$B_0={\mu }_0(M+H)$$(8)

Also, Maxwell’s equations hold under the assumption that anywhere within the flow, a local region exists that is large compared to the size of any particle but small compared to the distance over which the field would vary significantly:   

$$\nabla \cdot \mathit{B}=0$$(9)

Following the procedure employed by Rosensweig and Ciprios (1991), and by Brandani and Astarita (1996), the following general constitutive equations for the magnetic force can be derived:   

$$E_{\text{mp}}={\Psi }_{\text{mp}}\frac{B_0^2}{{\varphi }^2{\chi }_{\text{p}}{\mu }_0}$$(10)

  

$${\Psi }_{\text{mp}}={\left(\frac{\chi }{1+\chi }\right)}^2\left[\frac{\varphi }{\chi (1+\chi )}\frac{\partial \chi }{\partial \varphi }-1\right]$$(11)

  

$$E_{\text{mf}}={\Psi }_{\text{mf}}\frac{B_0^2}{{\varepsilon }^2{\chi }_{\text{f}}{\mu }_0}$$(12)

  

$${\Psi }_{\text{mf}}={\left(\frac{\chi }{1+\chi }\right)}^2\left[\frac{\varepsilon }{\chi (1+\chi )}\frac{\partial \chi }{\partial \varepsilon }-1\right]$$(13)

These equations are perfectly symmetrical, but are valid only for the two limiting cases of χ_f = 0 (the solid is magnetizable, Eqns. 10–11) or χ_p = 0 (the fluid is magnetizable, Eqns. 12–13). The corresponding expression for the magnetic forces is obtained by combining these equations with a constitutive relation for the bed susceptibility. It can be shown that, using the Clausius-Mossotti relationship (Banhegyi, 1986), the equations by Rosensweig and Ciprios (1991) are obtained:   

$$E_{\text{mp}}=\frac{18\varphi {\chi }_{\text{p}}^2}{{\left(3+{\chi }_{\text{p}}+2\varphi {\chi }_{\text{p}}\right)}^3}\frac{B_0^2}{{\mu }_0}$$(14)

  

$$E_{\text{mf}}=\frac{2\varepsilon {\chi }_{\text{f}}^2{\left(2{\chi }_{\text{f}}+3\right)}^2}{{\left(1+{\chi }_{\text{f}}\right)}^2{\left(3+2\varepsilon {\chi }_{\text{f}}\right)}^3}\frac{B_0^2}{{\mu }_0}$$(15)

4. Stability criterion

The kinematic and dynamic wave velocities can be derived following the linearization procedure of Wallis (1969) and Gibilaro (2001). Wallis’ theory states that voidage perturbation velocities in the bed are bounded by the kinematic wave velocity and the dynamic wave velocity. The kinematic wave velocity is obtained when the steady state flow depends on the voidage, and in a fluidized bed it is only a function of the drag equation (Wallis, 1969). On the other hand, the dynamic wave velocity is the speed at which voidage perturbations run through an elastic or compressible medium, resembling, e.g. sonic waves in a gas. This fundamental result was applied by Brandani and Zhang (2006) to the limiting case without magnetic forces and results in:   

$$u_{\text{k}}=\varphi {\left(\frac{\partial U}{\partial \varepsilon }\right)}_{\text{Equil}}=\frac{\varphi }{\varepsilon }\frac{4.8U}{2+\frac{\text{d}{C}_{\text{D}}}{\text{d}\mathit{Re}}\frac{\mathit{Re}}{C_{\text{D}}}}$$(16)

and the dynamic wave velocity:   

$$u_{\text{D}}=\sqrt{V^2-G}+V$$(17)

where, under the quasi-equilibrium approximation:   

$$V=\frac{\varphi }{\varepsilon }\frac{{\rho }_{\text{f}}U}{\varepsilon {\rho }_{\text{p}}+\varphi {\rho }_{\text{f}}}$$(18)

  

$$G=\frac{\frac{\varphi {\rho }_{\text{f}}{U}^2}{{\varepsilon }^2}-\delta (\varepsilon {\rho }_{\text{f}}+\varphi {\rho }_{\text{p}})g}{\varepsilon {\rho }_{\text{p}}+\varphi {\rho }_{\text{f}}}$$(19)

The superficial velocity U is calculated from the bed equilibrium relationship and the drag force is expressed as Gibilaro (2001), with the Dallavalle expression for C_D:   

$$F_{\text{D}}=\frac{3}{4}\frac{{\rho }_{\text{f}}}{d_{\text{p}}}{C}_{\text{D}}{U}^2\varphi {\varepsilon }^{-3.8};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{C}_{\text{D}}={\left(0.63+\frac{4.8}{\sqrt{\mathit{Re}}}\right)}^2$$(20a, b)

The criterion for minimum bubbling can be expressed in terms of a kinematic and a dynamic wave velocity as Wallis (1969): the bed is stable when the kinematic velocity is smaller than the dynamic wave velocity. In the presence of additional magnetic forces acting on the particles, the kinematic velocity remains unchanged, while only the G term is modified to the following expression that has to be adopted in Eqn.17   

$$G_{\text{M}}=G-\frac{18\varphi {\chi }_{\text{p}}^2}{{\left(3+{\chi }_{\text{p}}+2\varphi {\chi }_{\text{p}}\right)}^3}\frac{B_0^2}{{\mu }_0}\frac{\varepsilon }{\varepsilon {\rho }_{\text{p}}+\varphi {\rho }_{\text{f}}}$$(21)

For the investigated system, the prediction results are reported in Fig. 1 in terms of wave velocities (kinematic and dynamic) as a function of the fluid-phase volume fraction and magnetic field intensity.

Fig. 1

Kinematic (continuous line) and dynamic wave velocities (dashed lines) as a function of the magnetic induction.

When the magnetic field intensity is set to B₀ = 0.088 T or below, the minimum bubbling voidage ɛ_mb is below the voidage at minimum fluidization conditions ɛ_mf = 0.4 (typical of random particle arrangement): this is a characteristic of all Geldart Type B particles (always bubbling when fluidized).

Above B₀ = 0.088 T ɛ_mf > ɛ_mb, the particles behave as Geldart Type A powders, e.g. conditions exist in which homogeneous fluidization is feasible before bubbling occurs.

For B₀ = 0.1 T the minimum bubbling point is ɛ_mb = 0.423 and U_mb = 0.084 m/s, for B₀ = 0.15 T the minimum bubbling point is ɛ_mb = 0.531 and U_mb = 0.21 m/s. Notably, above B₀ = 0.188 T, the system is always stable since u_d>u_k at all flow rates.

5. CFD model

A set of test simulations were carried out to assess qualitatively the effect of the magnetic field on the fluidization regime. The aim is to verify the ability of the code in simulating whether the magnetic field is capable of suppressing the formation of bubbles in a bed that would normally be operating in the bubbling regime. In particular, a fluidized bed stabilized in LAST mode (i.e. magnetic field is applied to a freely bubbling fluidized bed) was simulated by CFD.

In the Eulerian-Eulerian approach to multiphase modeling, continuity and momentum balance equations in vector forms have to be solved for each phase (Eqns. 22–25):   

$$\frac{\partial \varepsilon {\rho }_{\text{f}}}{\partial t}+\nabla \cdot \left(\varepsilon {\rho }_{\text{f}}{\mathit{u}}_{\mathbf{f}}\right)=0$$(22)

  

$$\frac{\partial \varphi {\rho }_{\text{p}}}{\partial t}+\nabla \cdot \left(\varphi {\rho }_{\text{p}}{\mathit{u}}_{\mathbf{p}}\right)=0$$(23)

  

$$\begin{array}{r}\hfill \frac{\partial \varphi {\rho }_{\text{p}}{\mathit{u}}_{\mathbf{p}}}{\partial t}+\nabla \cdot \left\{\varphi \left[{\rho }_{\text{p}}{\mathit{u}}_{\mathbf{p}}\cdot {\mathit{u}}_{\mathbf{p}}-\eta \left(\nabla {\mathit{u}}_{\mathbf{p}}+{\left(\nabla {\mathit{u}}_{\mathbf{p}}\right)}^T\right)\right]\right\}\\ \hfill =\varphi \left(\mathit{B}-\nabla P_{\text{p}}\right)+{\mathit{F}}_{\mathbf{D}}+F_{\text{p}}\end{array}$$(24)

  

$$\begin{array}{r}\hfill \frac{\partial \varepsilon {\rho }_{\text{f}}{\mathit{u}}_{\mathbf{f}}}{\partial t}+\nabla \cdot \left\{\varepsilon \left[{\rho }_{\text{f}}{\mathit{u}}_{\mathbf{f}}\cdot {\mathit{u}}_{\mathbf{f}}-\eta \left(\nabla {\mathit{u}}_{\mathbf{f}}+{\left(\nabla {\mathit{u}}_{\mathbf{f}}\right)}^T\right)\right]\right\}\\ \hfill =\varepsilon \left(\mathit{B}-\nabla P_{\text{f}}\right)+{\mathit{F}}_{\mathbf{D}}+F_{\text{f}}\end{array}$$(25)

Of course, closure relations are also needed in order to properly model the particle phase and its interactions with the gas phase: for this purpose, the standard GKT model is adopted for estimating the rheological properties of the fluidized solid phase (Gidaspow, 1994) and standard drag models are adopted to estimate the momentum exchange between phases at the phase boundaries (as done by Brandani and Zhang, 2006). Complete details on the model equation implemented within the code can be found in the CFX documentation.

The additional forces due to the bed hydrodynamic elasticity (Eqns. 3–4: Brandani and Zhang, 2006; Busciglio et al. 2010) and the magnetic forces (Eqns. 14–15) were expressed as follows:   

$$F_{\text{f},y}=-E_{\text{f}}\frac{\partial \varepsilon }{\partial y};\hspace{0.17em}\hspace{0.17em}{F}_{\text{p},y}=+E_{\text{p}}\frac{\partial \varphi }{\partial y}$$(26a, b)

  

$$F_{\text{mp},x}=E_{\text{mp}}\frac{\partial \varepsilon }{\partial x};\hspace{0.17em}\hspace{0.17em}{F}_{\text{mp},y}=E_{\text{mp}}\frac{\partial \varepsilon }{\partial y}$$(27a, b)

  

$$F_{\text{mf},x}=E_{\text{mf}}\frac{\partial \varepsilon }{\partial x};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{F}_{\text{mf},y}=E_{\text{mf}}\frac{\partial \varepsilon }{\partial y}$$(28a, b)

The additional hydrodynamic forces, F_f,y and F_p,y, operate in vertical direction. Conversely, the magnetic body forces possess components in both the x and y directions. Maxwell’s model equation has been used to obtain the additional terms reported in Eqns. 27–28. These are implemented in the code, since all the parameters except the void fraction gradients are constants.

As far as the numerical aspects are concerned, CFD simulations were performed in a 2D fashion, choosing a time step interval in the range between Δt = 10⁻⁵ s and Δt = 10⁻⁴ s and a computational grid consisting of 0.005 m square cells, with 200 cells along the vertical direction and 30 cells along the horizontal direction, thus resulting in a vertical extension of the domain equal to 1.0 m and a horizontal extension equal to 0.15 m. Grid independence was assessed, checking to make sure that cells only half the size (0.0025 m square cells) of those actually adopted did not change the simulation results.

The initial condition for the particle bed height is equal to 0.5 m, with the solid volume fraction within the bed set equal to 0.60. The lateral walls were modeled using the standard no-slip boundary condition. The upper section of the simulated geometry, or freeboard, was considered to be occupied only by gas. A simple pressure boundary condition was imposed at the top of the freeboard (i.e. fully developed flow condition). A Dirichlet boundary condition was employed at the bottom of the bed to specify uniform vertical gas inlet velocity throughout the distributor. Symmetry planes were imposed on the front and rear faces of the simulated bed in order to perform the simulation in a proper 2D fashion. Symmetry planes placed at the boundaries along the width direction of the computational domain causes all variables to be mathematically symmetric with thus no diffusion across the boundary except for the component of velocity normal to the boundary which is anti-symmetric.

A typical Geldart type B system fluidized by air in magnetization LAST mode was simulated (d_p = 300 μm, ρ_p = 2500 kg/m³, χ_p = 10). The fluid velocity was equal to 2.5 U_mf, i.e. 0.22 m/s for the investigated system. The magnetic force is expected to cause particles to reduce their motion and form aggregates which are aligned along field lines. At high field intensity, the bed should eventually collapse, resulting in a fixed, anisotropic structure of particle aggregates.

A magnetic field, B, in the range between 0.05–0.6 T, was applied to a fully fluidized bed in order to stabilize the bed.

Each simulation was subdivided into the following three stages:

• • Starting from the initial steady condition of a settled bed, the gas inlet was simulated for 4s at Δt = 10⁻⁴ s. During this time interval, the bed evolves from the initial condition to freely bubbling in pseudo steady state condition. Because of the inlet gas velocities adopted, a freely bubbling regime generally develops.
• • The freely bubbling condition at 4s is used as the initial condition for a second simulation stage, in which the magnetic field is present. Because of the very rapid transient dynamics expected, a reduced time step was adopted, i.e. Δt = 10⁻⁵ s. In general, after 0.5 s subsequent to magnetic field application, the final steady state is practically achieved for the MSFB.
• • Finally, the simulation was carried out for a further 1s at a time step value of Δt = 10⁻⁴ s: this allows simulation of the stabilized regime in a reasonable time.

Typical CPU running times for this reference case were equal to about 4h for 1s of real time simulated with a fixed time step interval Δt = 10⁻⁴ s on a Dell Dimension 8300 Personal Computer.

6. Data analysis

Data obtained from the simulations were post-processed in order to quantify the effect of the superimposed magnetic field. The following instantaneous parameters were chosen:

• • the instantaneous polydispersity index of volume fraction distribution within the bed, PI, was chosen to characterize the uniformity of bed voidage. This parameter is defined as:   
  $$PI=\frac{{\varphi }_{21}}{{\varphi }_{10}}-1;\hspace{0.17em}\hspace{0.17em}{\varphi }_{ij}(t)=\frac{{\sum }_{y<H_0}{\left[\varphi (x,y,t)\right]}^i}{{\sum }_{y<H_0}{\left[\varphi (x,y,t)\right]}^j}$$(29a, b)
  where the general moment ratio ϕ_ij(t) is defined on the basis of the solid volume fraction values of the computational cells placed below the initial bed height H₀(t = 0). Notably, it was decided to analyze all the computational cells below the initial bed height to avoid measurement of the properties of the freeboard region. The larger the polydispersity index PI(t), the less uniform is the instantaneous volume fraction distribution inside the bed.
• • the instantaneous mean value of bed height, H₀, was chosen to characterize bed expansion below the initial bed height. The freeboard extent is computed as the average height if the upper domain region has a solid volume fraction below 0.15 (this is equivalent to the conventional transition value between the emulsion phase and bubble phase in fluidized beds).

7. Results

The first qualitative evaluation of the simulation ability to capture the typical behavior of a MSFB can be performed easily by observation of the particle volume fraction map sequences reported in Fig. 2. The maps report data about the glass ballotini simulation, d_p = 300 µm; fluidized at U = 2.5 U_mf with a magnetic field intensity ranging from B = 0.05 T to B = 0.6 T.

Fig. 2

Snapshot sequences of the simulated freely bubbling fluidized bed (0–4 s) and subsequent onset of magnetic-field-assisted fluidization (4–5.5 s). d_p = 300 µm; U = 2.5 U_mf; from top to bottom: a) B = 0.05 T; b) B = 0.1 T; c) B = 0.2 T; d) B = 0.4 T; e) B = 0.6 T

Taking as an example the sequence simulated at B = 0.2 T (Fig. 2b), which is immediately above the minimum stabilization field, it is possible to observe that the sequence embraces all stages from the initial condition to fully developed bubbling regime conditions (from 0.0 to 4.0 s), and the subsequent transitory due to application of the magnetic field (i.e. from 4.0 to 5.5 s) until steady state conditions are achieved.

It is worth noting that the code is able to simulate bubble formation correctly, at least in a qualitative way, and growth along the bed appears to be correctly predicted. Notably, after application of the magnetic field, the fluid dynamic regime suddenly changes toward a stabilized state. Under these conditions, all bubbles disappear in all cases simulated.

As it can be observed in Fig. 2a, when the magnetic field is set at values lower than 0.2 T, the stabilizing effect is able to partially damp out bubbles within the bed, but local in homogeneities are still evident. In this case, the applied field intensity was not sufficient to achieve a fully stabilized state. In all likelihood, the transition from partial to full bed stabilization can be found at magnetic field values close to B = 0.2 T as discussed earlier. In the case of higher field values (B = 0.4 and 0.6 T shown in Fig. 2d–e), the bed is fully stabilized but a longitudinal voidage gradient appears parallel to the field direction. Notably, this increases the bed volume occupied by the solid phase and the magnetic field also increases.

This effect can be theoretically predicted taking into account the one-dimensional momentum balances (Eqns. 1–2). At equilibrium, if there are no gradients in the void fraction of the bed, the bed weight must equate the drag force, hence it is possible to calculate the void fraction of the homogeneous bed, which for U = 0.22 m/s yields ɛ = 0.537. Most of the bed will be at this condition, except in the vicinity of the freeboard where a gradient in the void fraction is inevitable. At equilibrium, we can assume that u_p = 0, u_f = U/ɛ and all time gradients are nil. If the fluid and particle momentum balance are combined to eliminate pressure, the following differential equation is obtained:   

$$\frac{\text{d}\varepsilon }{\text{d}z}=\frac{F_{\text{D}}-\varepsilon (1-\varepsilon )({\rho }_{\text{p}}-{\rho }_{\text{f}})}{\frac{{\rho }_{\text{f}}(1-\varepsilon )U^2}{{\varepsilon }^2}-\varepsilon (E_{\text{MP}}-E_{\text{P}})-(1-\varepsilon )E_{\text{F}}}$$(30)

Eqn. 30 clearly shows that there will be a region between ɛ₀ = 0.537 and ɛ₁ = 1—where the RHS of the equation is zero—where there will be a transition. Eqn. 30 can be used to estimate the stratification at the free-board as a function of the magnetic field as shown in the figure below (Fig. 3)

Fig. 3

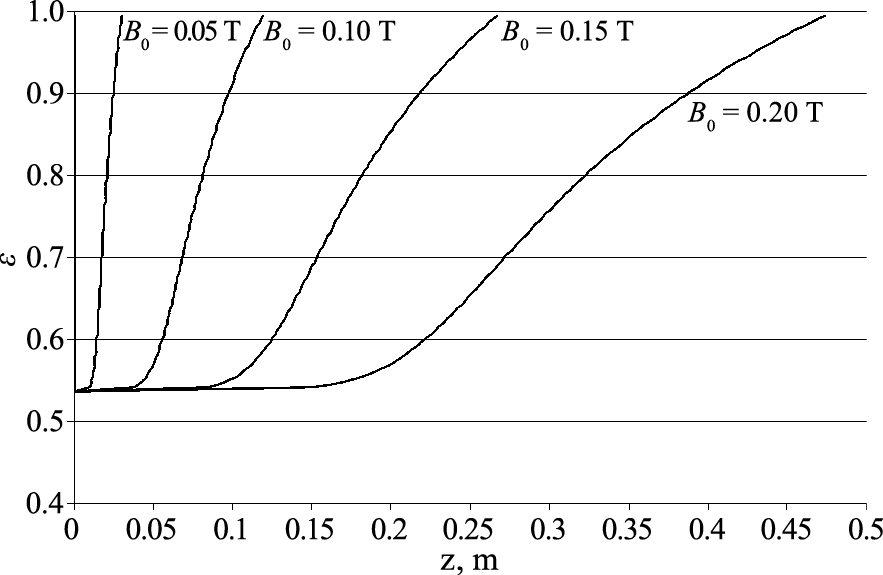
Profiles of void fraction in the proximity of the free-board region as computed by Eqn. 30 at different magnetic field intensities.

Clearly, further computational and experimental investigations are needed to investigate this behavior in detail, but the full simulations are clearly in qualitative agreement with the predicted effect. In order to quantify and compare the simulation results after the change in the applied magnetic field, in Fig. 4a the time evolution of the polydispersity index is reported for all the simulations shown in Fig. 2.

Fig. 4

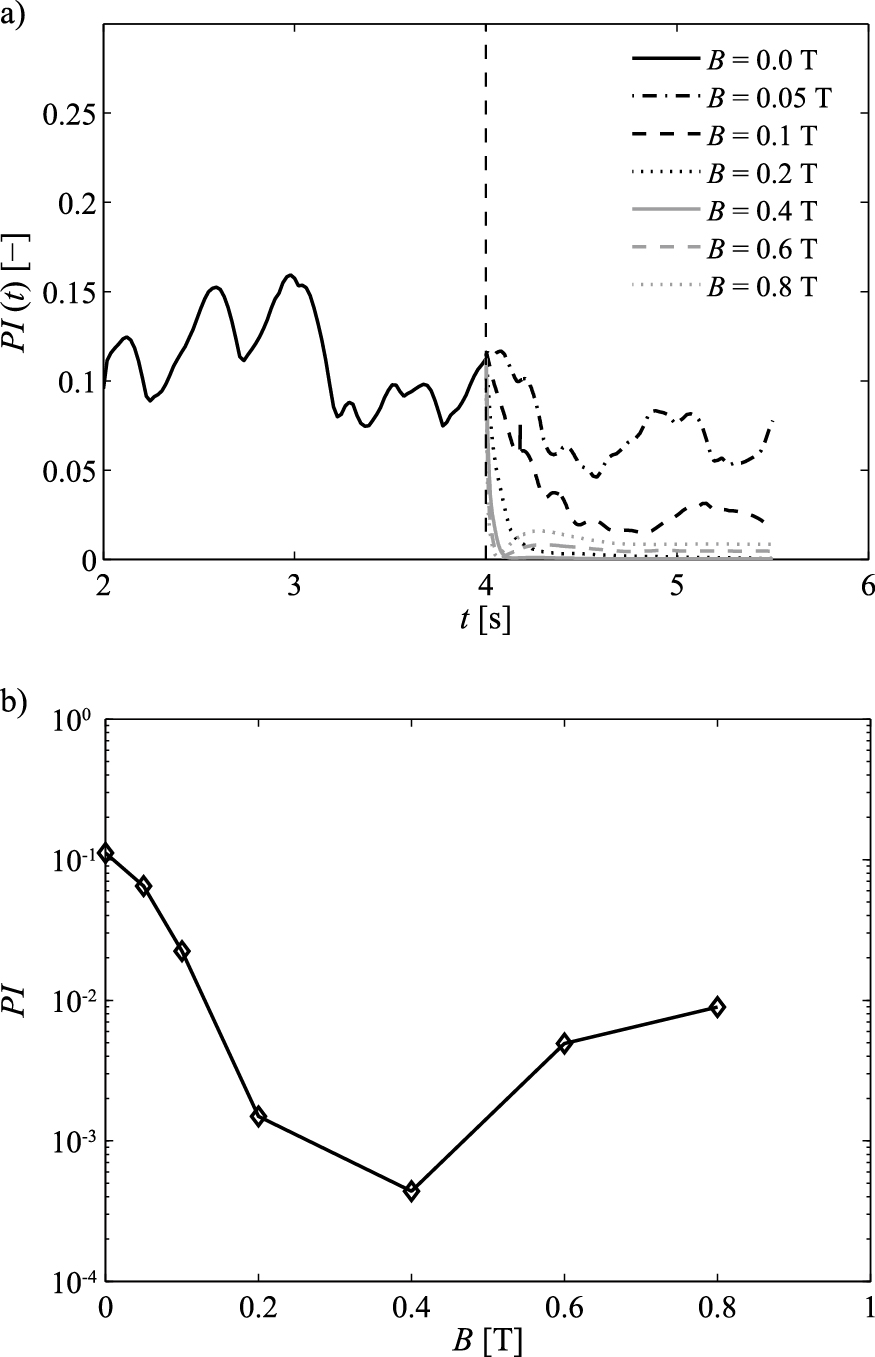
Time evolution of the polydispersity index at different magnetic field intensities (a) and relevant time-averaged values (b). d_p = 300 µm; U = 2.5 U_mf.

Before the onset of the magnetic field (t = 0–4 s), it is possible to observe high PI values with a markedly oscillating behavior due to the bubbles rising through the bed. After application of the magnetic field, a sudden decrease of the polydispersity index underlines the stabilization of the system for all cases investigated.

Notably, the effect of the applied magnetic field is practically instantaneous. Moreover, the quantitative analysis of PI shows the stabilizing effect that the magnetic field has on the bubbling bed: in the case of B < 0.2 T, the PI value decreases but still oscillates after the magnetic field onset, while higher magnetic field intensities give rise to a smooth and stable PI value. This is further confirmed by Fig. 4b, in which time-averaged PI values are reported as a function of the superimposed magnetic field intensity. It is possible to observe that at B values below 0.2 T, high polydispersity values are found because of incomplete bubble suppression, while at values higher than B = 0.4 T, even if complete bubble suppression occurred, the PI value increases slightly because of bed stratification.

Hence, these simulations confirm the ability of the model to predict the existence of a critical B value to achieve a fully stabilized bed.

Clearly, the onset of a diffused freeboard (qualitatively observed in Fig. 2 and further discussed in Fig. 3) can be quantified by showing the bed height H₀ as a function of time (as reported in Fig. 5a) and relevant time-averaged values (reported in Fig. 5b). Notably, the increase in the average bed height becomes important at a high magnetic field intensity (especially above B = 0.4 T).

Fig. 5

Time evolution of average bed height at different magnetic field intensities (a) and relevant time-averaged values (b). d_p = 300 µm; U = 2.5 U_mf.

Concluding, it is possible to point out that even if some limits are still present, because of intrinsic limitations of the multifluid approach (Eulerian-Eulerian) and magnetic model simplification, the CFD model adopted is able to capture the main characteristics of the MSFB with reasonable accuracy and within acceptable simulation times from an engineering point of view.

8. Conclusions and future aims

An Eulerian-Eulerian CFD model to simulate the behavior of the MSFB was successfully developed. The CFD model correctly predicts the onset of different stabilization levels depending on the intensity of the magnetic field applied and provides further insights on the behavior of MSFBs.

Even if work still has to be done with regard to the implementation of more comprehensive mathematical models (including inter-particle forces as an example), this result may be regarded as very promising, being among the first CFD simulations of MSFBs with Eulerian-Eulerian models.

Notation

B

body forces per unit volume [kg m⁻² s⁻²];

B

magnetic field strength [A m⁻¹];

d_p

particle diameter [m];

F_D

drag force per unit volume, [kg m⁻² s⁻²];

F_f

fluid-dynamic forces (fluid phase) [kg m⁻² s⁻²];

F_p

fluid-dynamic forces (solid phase) [kg m⁻² s⁻²];

F_mf

magnetic forces (fluid phase) [kg m⁻² s⁻²];

F_mp

magnetic forces (solid phase) [kg m⁻² s⁻²];

g

acceleration due to gravity [m s⁻²];

H

magnetization [A m⁻¹];

H₀

bed height [m];

PI

polydispersity index [–];

Th

threshold value for bed height calculation [–];

u

phase velocity [m s⁻¹];

U

superficial gas velocity [m s⁻¹];

U_mf

minimum fluidization velocity [m s⁻¹];

µ₀

vacuum magnetic permeability [A m⁻²];

δ

averaging length in momentum balance [m];

ɛ

fluid-phase volume fraction [–];

η

viscosity [Pa s];

ρ

density [kg m⁻³];

ϕ

particle-phase volume fraction [−];

χ

magnetic susceptibility [−];

Author’s short biography

Antonio Busciglio

Antonio Busciglio was born in 1982. He took the PhD in “Chemical and Materials Engineering” at Palermo University in 2011, where he continued his activity as a Research Assistant until 2014. Since September 2014, he is Assistant Professor at the University of Bologna, Department of Industrial Chemistry. His scientific activity focuses on experimental and computational analysis of multiphase flows (fluidized beds, unbaffled stirred tanks and sparged gas-liquid stirred tanks). He developed several experimental techniques based on image analysis for the characterization of multiphase flows. As a result, he authored of about 50 papers in international journals or conference proceedings.

Giuseppa Vella

Giuseppa Vella graduated in chemical engineering in 2001 and received her doctorate with a PhD thesis on the dynamics of fluidized beds. Her scientific activity focuses on the following research topics: CFD modelling of single and multiphase flows in stirred vessels, modelling and experimental investigation of photo-catalytic soli-liquid reactors for pollutant abatement, experimental analysis and CFD modelling of fluidized beds, fluid analysis of equipment for the production of thermal energy by pressure-retarded osmosis.

As a result of this activity, she authored 36 papers in international journals or in conference proceedings.

Giorgio Micale

Giorgio Micale joined University College London as a lecturer in chemical engineering in 2000, promoted to senior lecturer in 2002. From 2005, he has been associate professor of chemical engineering at Università di Palermo. His current research interests are: 1) mixing and multiphase flows in stirred tanks, 2) fluidization, 3) conventional and unconventional desalination processes coupled with renewable energy, 4) salinity gradient energy production. Contributions were made to developing novel experimental techniques and original simulations based on CFD methods. In 2001, he was awarded the “Young Researcher’s Award” by the Working Party on Mixing of EFCE and in 2014, the “Senior Moulton Medal” by the IChemE.

Stefano Brandani

Stefano Brandani holds the chair of the chemical engineering department at the University of Edinburgh. He is a member of the Directorate of the Scottish Carbon Capture and Storage Centre and is the UKCCS research area champion for adsorption and membranes. He joined the University of Edinburgh in 2007 where he leads the carbon capture group in the school of engineering. His research is aimed at the development of novel materials and processes for next-generation carbon capture applications. In 2001 he received a Philip Leverhulme Prize and a Royal Society-Wolfson Research Merit Award on Reducing Greenhouse Gas Emissions. In 2013 he was conferred the title of Cavaliere dell’Ordine della Stella d’Italia from the President of Italy. He has refereed over 100 publications in the fields of adsorption, fluidization and phase equilibria.

References

•  Anderson  T.,  Jackson  R., A fluid mechanical description of fluidized beds: Equation of motion, Ind. Eng. Chem. Fundamentals, 6 (1967) 527–539.
•  Banhegyi  G., Comparison of electrical mixture rules for composites, Colloid & Polymer Sci., 264 (1986) 1030–1050.
•  Brandani  S.,  Astarita  G., Analysis of the discontinuities in magnetized bubbling fluidized beds, Chem. Eng. Sci., 51(20) (1996) 4631–4637.
•  Brandani  S.,  Zhang  K., A new model for the prediction of the behaviour of fluidized beds. Powder Technol., 163(1–2) (2006) 80–87.
•  Busciglio  A.,  Micale  G.,  Vella  G.,  Rizzuti  L., Linear stability analysis of gas-fluidized beds for the prediction of incipient bubbling conditions, Chem. Eng. J., 157 (2010) 489–500.
•  Foscolo  P.,  Gibilaro  L., Fluid dynamic stability of fluidised suspensions: the particle bed model, Chem. Eng. Sci., 42 (1987) 1489–1500.
•  Geldart  D., Gas Fluidization Technology, John Wiley & sons, 1973.
•  Gibilaro  L.,Fluidization Dynamics, Butterworth-Einemann, Oxford, UK, 2001.
•  Gidaspow  D., Multiphase flow and fluidization, Academic Press, San Diego, 1994.
•  Hristov  J., Magnetic field assisted fluidization—a unified approach. Part 1. Fundamentals and relevant hydro-dynamics of gas fluidized beds (batch solids mode), Reviews in Chemical Engineering, 18(4–5) (2002) 295–509.
•  Hristov  J.,  Ivanova  V., Magnetic field-assisted bioreactors, in:  Kawai  F.,  Sasaki  K. (Eds.), Recent Research Advances in Fermentation and Bioengineering, vol. 2, SignPost Research, Trivadrum, 1999, pp. 41–94.
•  Ishii  M., Thermofluid dynamic theory of multiphase flow, Eyrolles, Paris, France, 1975.
•  Jackson  R., The dynamic of fluidised particles, Cambridge University Press, New York, USA, 2001.
•  Kirko  I.,  Filippov  M., Standard correlations for a fluidized bed of ferromagnetic particles in a magnetic field, Zn Tekhniko Fizika, 30 (1960) 1081–1090.
•  Kunii  D.,  Levenspiel  O. (Eds.), Fluidization Engineering, Butterworth-Heinemann, Massachusetts, USA, 1991.
•  Li  X.,  Sun  D.,  Chen  J.,  Wang  S.,  Bai  Y.,  Lu  H., Numerical simulation of magnetic particles flow behaviour in a gas-solid fluidized bed with gradient magnetic field, Journal of Chemical Engineering of Chinese Universities, 24(1) (2010) 52–57.
•  Rosensweig  R., Process for operating a magnetically stabilized fluidized bed, U.S. patent, number 4115927, 1978.
•  Rosensweig  R., Magnetic stabilization of the state of uniform fluidization, Ind. Eng. Chem. Fundam., 18(3) (1979) 260–269.
•  Rosensweig  R., Ferrohydrodynamics, Cambridge University Press, USA, 1985.
•  Rosensweig  R.,  Ciprios  G., Magnetic liquid stabilization of fluidization in a bed of non-magnetic particles, Powder Technol., 64(1–2) (1991) 115–123.
•  Saxena  S.,  Shrivastava  S., Some hydrodynamic investigations of a magnetically stabilized air-fluidized bed of ferromagnetic particles, Powder Technol., 64(1–2) (1991) 57–67.
•  Siegell  J., Liquid-fluidized magnetically stabilized beds, Powder Technol., 52(82) (1987) 139–148.
•  Wallis  G.G., One-Dimensional Two-Phase Flow, McGraw-Hill, New York, 1969.
•  Wang  Y.H.,  Gui  K.,  Liu  L.,  Shi  M., Numerical simulation of gas-solid flows in MFBs and experimental demonstration, Journal of Southeast University (Natural Science Edition), 32(6) (2002) 936–940.
•  Webb  C.,  Kang  H.,  Moffat  G.,  Williams  R.,  Estevez  A.,  Cuellar  J.,  Jaraiz  E.,  Galan  M.A., The magnetically stabilized fluidized bed bioreactor: A tool for improved mass transfer in immobilized enzyme systems, Chem. Eng. J., 61(3) (1996) 241–246.
•  Xu  S.,  Guan  Y., Numerical simulation and experimental validation of magnetic medium performance in air-dense medium fluidized bed. Int. J. of Coal Preparation and Utilization, 23(1–2) (2003) 57–65.