From Quasi-static to Intermediate Regimes in Shear Cell Devices: Theory and Characterisation

Abstract

The design of new technology for processing and manufacturing particulate products requires understanding granular rheology over a broad range of conditions. Powders display a complex behaviour due to their ability to rearrange under stress, and as a result, granular flow is generally classified into three flow regimes, namely a quasi-static regime dominated by frictional contacts, an inertial regime dominated by collisional and kinematic stresses and an intermediate regime where the three sources of stress are important to establish a stress-strain rate relationship. Characterisation of the flowability is generally restricted to the flow initiation in quasi-static regime, even if, transition into inertial conditions is very common in practical applications involving the control of dense flows, such as powder handling, particle formation processes or additive manufacturing. This work presents a critical review of available techniques to characterise the departure from the quasi-static regime into an intermediate flow. We revise the application of shear cells and present different strategies to modify classic devices with external actuation, such as aeration, to operate at higher inertial numbers. We pay particular attention to innovative designs using aerated Couette flow configurations, highlight the complexity in the standardisation and the challenges in advancing towards a universal model.

1. Introduction

A universal description of granular rheology is both a fundamental and industrial challenge. Complex granular flows are a feature of natural phenomena such as landlines, rock slumping and sand dunes as well as in industrial processes such as granulation, milling and fluidisation. Powders, particulates and gravels are often the scaffolds where complex biological, physical or chemical processes take place, and underpin disciplines spanning from geomechanics (Wheeler and Sivakumar, 1995) to volcanology (Petford, 2003), including the study of dense flows such as soil (Pastor et al., 2009) and sediments (Baumgarten and Kamrin, 2019). Powders constitute a large proportion of raw materials, intermediates, products and waste in the primary and the process industry, and the energy, environmental and manufacturing sectors. Pigments, ceramics, petrochemicals, plastics, bulk and fine chemicals or fast-moving consumer goods are only some examples.

Although powders have been studied for a century, our understanding of granular flow is far from that of simple fluids or solids. Individual particle interactions lead to a collective behaviour that makes powders restructure under stress. If compressed, they respond as an elastic solid; but when diluted, they behave like a fluid (Jaeger et al., 1996). Solid-like behaviour steams from the formation of a network of contacts, the so-called force chains, that transmit the stress. In addition to these frictional contacts, particle interactions are altered by a broad range of forces from electrostatics and van der Walls to liquid and solid bridges (Hartmann and Palzer, 2011). The dissipation and storage of energy in the force chains allow a bed of particles to remain static and fail only under the application of a given stress. But as the flow becomes more rapid, force chains reorganise and break. When the deformation (strain rate) is faster than the ability for the force chains to recombine, they can no longer transmit and absorb stress, and the material restructures creating a fluid-like relation between the applied stress and strain rate (Campbell, 2006). As a powder dilates, the free space between individual grains increases and the transport of momentum becomes dominated by instantaneous collisions of nearby particles. For sufficiently diluted cases, the flow displays a gas-like behaviour where collisions are rare, and the motion of each grain is uncorrelated from its neighbours.

The changes in the stress-strain rate relation are related to how grains reorganise and how the local force network responds to structural properties such as particle concentration, size and shape. Understanding the transition between different flow behaviours is crucial to develop new technologies because solid operations span a wide range of particle concentration, consolidation stress and shear rate. The design of a powder processing plant involves flows spanning from dilute inertial systems, such as in pneumatic transport, to slow frictional flows in storage, packaging, tabletting, or agglomeration devices like roller compaction (Wu et al., 2010) or twin-screw granulation (Dhenge et al., 2013). Operations such agglomeration in high shear mixers (Knight et al., 2001) or fluidised bed granulators are designed to work under dense conditions and display local transitions between solid and liquid-like behaviour (Mort, 2009). In many cases, this happens in an uncontrolled way through the agglomeration and deposition of cohesive powders in multiphase reactors, heat exchangers (Diaz-Bejarano et al., 2017) or spray dryers (Francia et al., 2015).

No universal framework unifies the description of granular rheology, and therefore, industry relies heavily on empirical characterisation to classify the flowability of powders. The earliest attempts used scores based on flow tests such as the Carr (Carr, 1965), and Hausner (Hausner, 1967) ratios, or more recently the Taylor composite index (Taylor et al., 2000). The use of properties such as unconfined yield strength or tensile strength is also common, but the flowability function, FF, defined as the ratio of the major principal stress to the unconfined yield stress in the powder, is perhaps the most utilised metric to characterise powder flow (Hassanpour et al., 2019). The characterisation is typically limited to identify a flow threshold, that is, the stress required to initiate flow, and it rarely extends into studying the dynamic flow properties. The work of GDR Midi (Midi, 2004) describes in detail the characteristics of granular flows in six typical experimental configurations. Those where the stress is imposed, such as heaps, drums, annular flows and inclined planes display a hysteresis in the yield stress. A given stress is required to establish a dense flow, but much smaller stresses are needed to maintain it. The yield point itself depends not only the particle properties but also on the stress history of the sample. All typical flow configurations (Fig. 1) show a complex flow pattern where dense areas governed by enduring frictional contacts interplay with other more dilute ones driven by instantaneous particle collisions. Ultimately, all develop complex velocity distributions varying from a localised shear band in the confined systems to linear and exponential decays in free surface flows. Given that the behaviour of a powder varies drastically from one to another, it is required to carry our several static and dynamic tests to properly evaluate the flowability as close as possible to the desired design conditions (Krantz et al., 2009).

Fig. 1

Typical configurations to study granular flow: (a) Couette (b) rotating drums and flows in (c) chutes e.g. parallel planes, inclined, vertical (d) and heaps.

Most available tests focused on the flow initiation and suffer from two limitations: transportability and universality. The discrepancies observed across different devices (Koynov et al., 2015) are a reflection of an overly simplified description of the system and inconsistencies in the experimental procedures. The effect of the stress history of a sample is well-known (Swize et al., 2019), but without a common way to condition the powder, it is challenging to draw any direct comparison between different tests and samples. The measurements are also not universal. The most established techniques are shear cells limited to a quasi-static flow (Schwedes, 2003). It is a consequence of the practical difficulty in studying inertial systems and the historical need to inform the design of silos. Although it is key to understand a dense granular flow (Sundaresan, 2001), the characterisation of dynamic properties is still far from the same level of detail.

Recent works have summarised the scope of the techniques available today to study the flowability of powders (Ogata, 2019), and the challenges involved in developing reliable dynamic tests for the study of caking and cohesive materials (Ghadiri et al., 2020). They discuss in detail the effects of properties such as size and shape, cohesion and how the interstitial fluid and the applied stress affect the flowability. Here, we will focus on the latter and specifically discuss the characterisation of the transition between two extreme flow regimes, namely solid-like and fluid-like flow, in a shear device. We provide an overview of the design and application of classic units and discuss the strategies to develop similar tests in modified devices that can cover a broader range of shear and consolidation stresses. The manuscript is organised as follows: Section 2 introduces the granular flow regimes and presents a brief overview of the mathematical modelling of granular flows. A brief review of the characterisation of the flow threshold, including a summary of shear cells is given in Section 3. The strategies to re-design the conventional shear devices to experimentally capture the transition from solid-like to fluid-like behaviour using an external actuation are discussed in Section 4, followed by conclusions and suggestions for future work.

2. Rheology of granular flows

2.1 Flow regimes

The flow behaviour of granular material depends on the applied stress, particle concentration and the effects of the interstitial fluid. If the concentration is high or close to the maximum packing, the material exhibits solid-like behaviour where stresses are transferred with frictional contacts between grains and slip layers move relative to each other along the applied shear. In this regime, namely frictional or “quasi-static” regime (Fig. 2a), the contacts between grains have a long duration, and deformation of the grain layers occurs very slowly (Campbell, 2002). Due to a highly dense concentration of particles, there is no much free space for the interstitial fluid, and its effects are usually neglected. In the quasi-static regime, flow is often studied by using soil mechanics principles or more specifically, plasticity models detailed in the next section. On the contrary, when the applied stress or the external energy transfer is sufficiently high, the particles have enough inertia to leave their layers and flow more independently. This flow regime is referred to as “rapid flow” or “inertial” regime. Here the transport processes are considered governed by binary instantaneous particle-particle collisions and random motions (Fig. 2a). With an analogy with the kinetic theory of monatomic gases, the concepts of the so-called granular thermal energy or “granular temperature” and the random fluctuating kinetic energy of particles are introduced in the framework of continuum modelling. The main formal differences between inertial granular flows and molecular gases are the finite size of particles and the non-equilibrium behaviour. The particle-particle collisions are dissipative; therefore, the fluctuating kinetic energy of the particles is dissipated to thermodynamic heat. The applied shear generates fluctuating kinetic energy through collisional and kinematic stresses (Fig. 2b). For a collisional stress, any collision between particles moving at their mean velocity in a simple shear will enhance random motion and lead to a velocity fluctuation quantified in the granular temperature. However, for a kinematic stress, the motion of a particle parallel to a velocity gradient generates a random velocity along its path (Fig. 2bii) and a source of anisotropy in the fluctuating kinetic energy.

Fig. 2

Granular rheology. Sources of (a) stresses (kinematic, collisional and frictional) in a quasi-static, an intermediate and an inertial flow regime for varying inertial number I, normal stress σ, shear rate $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ and solid fraction ɛ_s (b) generation of fluctuating kinetic energy in kinematic and collisional mechanisms.

For inertial granular flows with low and moderate solid concentrations, the interstices between the particles are far larger than in the quasi-static regime. These spaces are filled with fluid, and the granular material is then described as a multiphase flow, referred to as a gas-solid suspension, where the fluid-particle interactions become significant on the momentum transfer between phases. Many advanced formalisms, however, focus on a collision-dominated regime and disregard the effect of interstitial fluid. Other effects typical of real-life scenarios like shape, polydispersity or interparticle forces are often excluded from a continuum formulation. In the extreme of a very dilute (kinematic) gas-solid suspension, particle-particle collisions never happen, and the solid phase momentum simply diffuses as the particles travel through the medium (Tsao and Koch, 1995). Their motion is mainly driven by the carrier fluid and the interstitial fluid contributes to the particle stresses with a covariance between particle and fluid fluctuations (Koch, 1990). Gas-solid suspensions are not within the scope of this review, and comprehensive discussions are available elsewhere (Fan and Zhu, 2005).

In between these two extreme regimes, there exists an intermediate regime with a characteristic particle contact time larger than the instantaneous collision time but lower than an enduring contact. It lies between the quasi-static state dominated by frictional forces and the inertial state dominated by collisional stresses, and therefore, affected by both. This work concerns with the experimental characterisation of such a system. From a phenomenological modelling view, the transition between regimes can be characterised by the inertial number, I, given by Jop et al. (2006), as a scaled shear rate quantifying the interplay of the consolidation and the shear stress acting on a particle:

  

$$I=\frac{\dot{\gamma }\hspace{0.17em}d}{\sqrt{\sigma /\rho }}$$(1)

  

$$I=\frac{t_{\sigma }}{t_{\gamma }}=\frac{\sqrt{\sigma /\rho }/d}{1/\dot{\gamma }}$$(2)

I can be interpreted as the ratio between the time scale associated with the consolidation and the time scale of the strain as given in Eq. (2). As discussed in GDR Midi (Midi, 2004), the shear or deformation time scale, t_γ, can be though to represent the time needed to create a deformation by moving the top layer applying a shear stress, τ. The confinement scale, t_σ, represents the time needed to reorganise this structure pushing the top layer to its lower position and creating a packed system. Fig. 3 illustrates the concept shearing a granular layer. If the confinement is very quick compared to the deformation, the system will remain structured at a high concentration. On the contrary, if σ is not high enough to preserve the confinement, the system dilates. In the limit of I→0 a powder remains in a quasi-static state and the system behaviour is independent of the shear rate and purely controlled by a constant ratio between the shear and the normal stresses, τ⁄σ, denoted by different authors as apparent viscosity, μ_a or η_a, or the bulk, μ_b, or effective, μ_eff, friction coefficient or angle of internal friction. In practical terms, even in a quasi-static flow t_σ cannot tend to zero, and in reality, the grains experience rearrangements and slow displacements that result in intermittent dynamics. When the inertial number, I, increases, the particle inertia starts to play a significant role in the transport of momentum, and the system behaviour becomes dependent on the shear rate.

Fig. 3

Depiction of the inertial number I as the ratio of the deformation and compression timescales, t_γ and t_σ.

2.2 Overview of mathematical modelling

This work does not intend to review the modelling of granular flows. Here we present a brief overview of the phenomenological, theoretical and computational approaches used to described granular flows in the context of shear-cell devices. We refer the interested readers to Capriz et al. (2008) and Rao and Nott (2008) for a boarder discussion and comprehensive reviews on kinetic theories, plasticity, continuum and discrete modelling of granular flow and the relevant references.

A continuum description is the preferred way to describe granular flow in industrial processes handling billions of particles. For quasi-static flows, the theory of plasticity is often used to develop continuum models. Specifically, the plasticity theory determines the normal, σ, and shear stresses, τ, as a function of the strain rates (changes in the distance of adjacent particles with time in the neighbourhood of a point). In a slow regime, the frictional stresses are independent of the strain rate, and under a normal stress, granular material will shear only when the shear stress, τ, exceeds a critical value. The failure behaviour is simply described by a yielding law such as a Mohr-Coulomb criterion but yielding laws do not provide information on how particles flow or blocks of particles deform. To overcome this limitation, plastic potential theories are complemented with the critical state theory using yield and potential functions. Chen and Mizuno (1990) proposed a pathway to relate the applied stress to the deformation and Vun et al. (2010) listed the procedure to follow: (i) define a yield function, (ii) apply a plastic potential function to relate the rate of strain tensor to stress and (iii) set up a flow rule that links the yield function to the plastic function. The proposed quasi-static models feature different yield functions. For example, Srivastava and Sundaresan (2003) used the extended von Mises function, while Christakis et al. (2006) developed a viscoplastic model based on the Drucker-Prager plasticity function. The extended von Mises yielding law-based models was criticized (Dartevelle, 2004) for not accounting for energy dissipation and predict infinite dilatancy, but these physical inconsistencies are removed with a 3-D “compressible” formulation (Gray and Stiles, 1988). The limitations of these functions are discussed by Andreotti et al. (2013).

Rapid granular flows have been investigated by experimental studies and statistical mechanical methods. The well-known experimental study of Bagnold (1954) where spherical spheres were sheared in a coaxial cylinder rheometer, is the pioneering work on the constitutive behaviour of inertial granular flows. This heuristic study showed that the solid stresses, σ and τ, were a function of the square of the applied shear rate, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, at high rotating velocities. From the view of the theoretical modelling, the Kinetic Theory of Granular Flow (KTGF), an extension of the classical kinetic theory of gases to dense and inelastic granular flows, has been developed for forty years (Garzó and Dufty, 1999; Lun et al., 1984; Yang et al., 2016). In the KTGF approach, the granular material is modelled as a continuum medium, and the transport equations for solid concentration, momentum and granular temperature are derived. The square relation between the solid stress and the shear rate has been theoretically confirmed by KTGF models. Early comparisons of with annular-shear-cell test measurements were first reported by Lun et al. (1984) and later on several other studies (Hanes and Inman, 1985; Hsiau and Jang, 1998; Orlando and Shen, 2012). However, these experimental configurations provide information on the bulk behaviour of the granular material and not the motion of individual grains. Further comparisons of KTGF predictions with local granular measurements include the work of Wildman et al. (2008) where positron emission particle tracking (PEPT) was used to measure solid concentration and mean velocity profiles inside a three-dimensional annular shear cell.

Besides a continuum formulation, granular material can be studied by computational approaches such as Discrete Element Modelling (DEM) where individual particles are tracked via a Lagrangian approach solving Newton’s equations of motion and describing particle-particle collisions with a soft sphere model (Guo and Curtis, 2015). These simulations are classified as highly resolved because they can provide flow properties at particle-scale such as velocities, contact number and forces. Due to the high demand for computational resources, the method is applicable for academic studies and small-scale laboratory experiments. DEM simulations capture the persistence of a Bagnold regime (da Cruz et al., 2005) in homogeneous shearing of particles in fully periodic domains with Lees-Edwards boundary conditions, and are used to investigate boundary effects on confined geometries such as Couette flows (Vescovi et al., 2014).

The intermediate regime was first experimentally identified in inclined plane chutes (Pouliquen, 1999) and later in a Couette shear cell (Tardos et al., 1998), where the shear stress τ was found to depend on the strain rate to a power of between 0 and 2 that is a function of the solid concentration. While continuum models are available for quasi-static and inertial granular flows, the closures for the intermediate regime are still under debate. Johnson and Jackson (1987) proposed a semi-empirical model that super-imposed collisional and frictional stresses modelled with a critical state and an algebraic function of solid concentration. A similar “additive” approach was applied by (Savage, 1998) with using von Mises yield criterion. From a more empirical point of view, Jop et al. (2006) unified these two extreme regimes with a simple visco-plastic constitutive law without any fitting parameter and validated their model with experiments of a granular pile flowing between rough sidewalls. The model is called the μ(I) model. It is based on the Coulomb criterion and a bulk friction coefficient function of the inertial number, I, Eq. 1. Similarly, da Cruz et al. (2005) performed DEM simulations of plane shearing with frictional, inelastic disks and found that small values of I correspond to the quasi-static regime of soil mechanics, while large values correspond to the collisional regime of the KTGF.

There have been different ways to incorporate the frictional contribution of a dense flow into the KTFG (Wu et al., 2020). For example, Chialvo et al. (2012) carried out homogeneous shear DEM simulations of frictional and frictionless particles in the quasi-static and inertial regimes, and proposed corrections to the model of Garzó and Dufty (1999) to bridge these regimes using the μ(I) rheology model. Similarly, Vescovi et al. (2014) performed DEM of wall-bounded plane shearing of particles and used the expression for the correlation length developed by Berzi (2014) to modify the model of Garzó and Dufty (1999). Jenkins (2006) proposed a phenomenological correction to the rate of collisional dissipation in the KTGF model that describes the decrease in dissipation of fluctuations during enduring contacts. There are several studies that attempt to expand the μ(I) models to a non-local rheology, for example, using additional transport equations to describe a weight function between fluid and solid-like parts of the stress tensor (Aranson and Tsimring, 2001; 2002), or proposing new closures for μ_b dependent on coordination number and the evolution of a fabric anisotropy tensor (Sun and Sundaresan, 2011). An application of non-local μ(I) rheology in quasi 2-D shear cell experiments has also been given by Tang et al. (2018).

3. Quasi-static characterisation: shear cells

Shear cells are experimental devices designed to evaluate the flowability of a powder finding the relation between applied normal stress, σ, and the shear stress, τ, required for a static powder bed to fail. The operate performing shear tests by applying two orthogonal stresses on a sample and measuring its response. The first stress is denoted by the normal or consolidation stress, σ (see Fig. 4a). σ is often aligned with the gravity acceleration and includes the weight of the powder. The second stress is orthogonal to the first one, and denoted by the shear stress, τ. It is increased gradually until the sample reaches its yield point and starts flowing. Shear tests include two steps, a so-called pre-shearing test followed by the application of four to six different shear stresses. The objective of the pre-shearing test is to create a reproducible structure in the powder by applying a reference consolidation stress. The sample is consolidated at high normal stress, σ_pr, and then it is sheared until it fails and the recorded shear stress, τ_pr, reaches a constant value, denoted steady-state conditions. The pre-shearing normal and shear stresses (σ_pr,τ_pr) set a reference point for the study (blue point - Fig. 4b). At this point, if the shear stress is removed, the displacement ceases, but the sample reorganises into the same structure and so it exhibits the same response when it is sheared further. After the preparation stage, several experiments are conducted varying σ and τ, denoted “shear tests” or “shear points” (red - Fig. 4b). The sample is sheared to the failure point with a decrease in the consolidation stress (σ < σ_pr). For each value of σ, the shear stress corresponding to the bed failure, τ, is recorded and reported in a (τ,σ) diagram to build the yield locus line: τ = μ σ + C where μ is the angle of internal friction and C is the cohesive strength. The locus line describes the yield stress in quasi-static granular flow, it takes the form of a Coulomb behaviour where the yield stress is independent of the shear rate. It should be noted that the state of stress achieved in the sample after the pre-shearing is particular to each device, which introduces a degree of specificity to the method.

Fig. 4

(a) A granular layer under shear, τ, and consolidation, σ, stress. (b) Yield locus line, τ = μ σ + C; μ: angle of internal friction; C: cohesive strength; UYS, MPS: unconfined yield stress and major principle stress.

The angle of internal friction, μ, is reported as the slope of the yield locus line connecting all (τ,σ) pairs. In other words, the ratio between the shear and normal stresses τ/σ required for a sample consolidated at (σ_pr,τ_pr) to yield. Mohr circles are used to derive other important parameters. The principal stresses are defined as the base of the stress tensor that creates no shear stress in the system and therefore, minor and major, MPS, principal stresses can be obtained as the intersection of a Mohr circle with the axis τ = 0. A Mohr circle tangent to any point in the yield locus line is a representation of the conditions for critical failure at that combination of σ and τ. The principal stresses that describe the structure of the powder sample are obtained from the Mohr circle that contains the reference (σ_pr,τ_pr) and is tangent to the yield locus. The unconfined yield stress, UYS, is defined as the normal stress required for the powder to yield under no shear. It is obtained from the Mohr circle that contains the origin (a sample sustaining no stress) and the yield locus line. There are other definitions of the locus line stemming from shear tests. The bulk (or effective) μ_b friction factor defined from a bulk yield locus line (τ = μ_b σ) that contains the origin and is tangent to the Mohr circle of the pre-sheared sample. The relation between the shear and the normal stress in the pre-shearing point is given by τ = μ_ss σ with μ_ss the steady-state angle of internal friction. The flowability function, FF, is reported as the ratio of MPS to UYS.

Shear cells, or testers, can be classified into two categories: direct and indirect testers. In a direct tester the geometry of the device imposes a sheared region on the sample, whereas in an indirect tester, the sheared zone in the powder develops independently according to the stress applied. Many indirect testers such as the uniaxial, bi-axial and tri-axial testers were developed for specific applications and are generally not commercially available (Feise and Schwedes, 1995; Jenike, 1970; Schwedes, 1996). This work will focus on describing succinctly direct units, particularly examples of commercially available translational and recent rotational devices. More comprehensive details of the design and the historical development of shear cells can be found in the literature (Schwedes, 2003).

3.1 Jenike type translational testers

The working principle of translational shear testers is creating shear by sliding one section of the sample. Jenike provided one of the first translational devices used to study flowability (Jenike, 1970) and design silos, leading to an ASTM standard (Carson and Wilms, 2006). It consists in a container, or cup, with a stationary base and an upper ring subject to shearing. The cup is filled with a powder sample, and the lid is used to compact it by applying a constant vertical force (Fig. 5a). A horizontal force is applied to the top ring until the bed fails and starts to slide. Fig. 5b depicts the typical evolution of the shear stress, τ, in the pre-shearing and shearing steps. In a Jenike test, the steady-state flow condition is met when one observes a no changes in τ_pr under the pre-shearing normal stress, σ_pr. In a successive step, τ is set to zero removing the force and is σ is reduced. The sample is sheared gain, and the value of τ at the failure point is recorded as the first shearing point. Additional tests using new samples are required to obtain each point of the yield locus (Fig. 5b). The simplicity of the test made it widely accessible to industry as a way to rank powders and study the effects of environmental conditions, composition, moisture, size and shape. However, this simple configuration comes with a significant limitation. The cell has a short shearing path, limited by the maximum displacement, and for that reason, it does not allow for a continuous test. A new sample is needed to measure each shear point, which leads to a time-consuming process with a substantial intervention of the operator, and thus prone to error.

Fig. 5

Translational testers. (a) Cross-section of a sliding device (b) Qualitative illustration of the evolution of the shear stress during the experimental procedure.

Several works tried to overcome this limitation introducing a “constant volume methodology” (Duffy and Puri, 1999; Ladipo and Puri, 1997; Schulze, 2008; Tsunakawa and Aoki, 1982) whereby the Jenike tester is modified to operate continuously. After the steady-state flow is achieved at the prehearing test, σ is gradually reduced at a small speed releasing the load on the lid. The corresponding evolution of the shear stress, τ, is recorded to construct the yield locus line. The main advantage is the ability to perform a single continuous test measuring the evolution of the sample from the point (σ_pr,τ_pr) to the point C using one sample (green line - Fig. 4b). The early versions of the constant volume translational testers were subject of criticism (Schwedes, 2003) because of their complex configuration. It has been suggested that this methodology tends to underestimate the unconfined yield stress, nevertheless, to the best of our knowledge, no detailed direct comparatives confirm such a feature.

More recently, Shimada et al. (2018a; 2018b) developed a new device to evaluate flowability using a constant-volume shear tester. The methodology aims at providing continuous measurement of shear stress from a high consolidation point under no shear (σ_cvt,0), through the steady-state flow reference state (σ_pr,τ_pr) until the point at zero normal stress (C,0). The line from the point (σ_cvt,0) to the point (σ_pr,τ_pr) (purple line, Fig. 4b) is referred to as the “consolidation yield locus”. The configuration of the tester is depicted in Fig. 6. The upper section of the cell can be filled with a varying height of powder, allowing one to conduct tests at a constant and controlled void fraction. Once the powder is loaded in the cell, a vertical servo motor lowers the piston compressing the sample to the desired stress (σ_cvt,0). When the value is reached, the vertical motion stops at a fixed position for 2 min to relieve the excess stress. Afterwards, the horizontal servo motor applies a shearing force on the lower section until the shear stress reaches a constant value, τ_pr, registering the transition from (σ_cvt,0) to (σ_pr,τ_pr) directly (purple line - Fig. 4b). Next, the consolidation stress, σ, is reduced to zero by gradually lowering the vertical translation stage, reducing the shear stress from τ_pr to C (green line - Fig. 4b). The set up allows having a three-dimensional relationship between τ, σ and particle concentration ɛ_s. It is comparable to historical testers and obtains the yield locus line in a single test of one sample. However, it is still restricted to the length of the shearing path. While these testers are not widely available, the reports involve the use of fine powders and the possibility to use small consolidation stresses.

Fig. 6

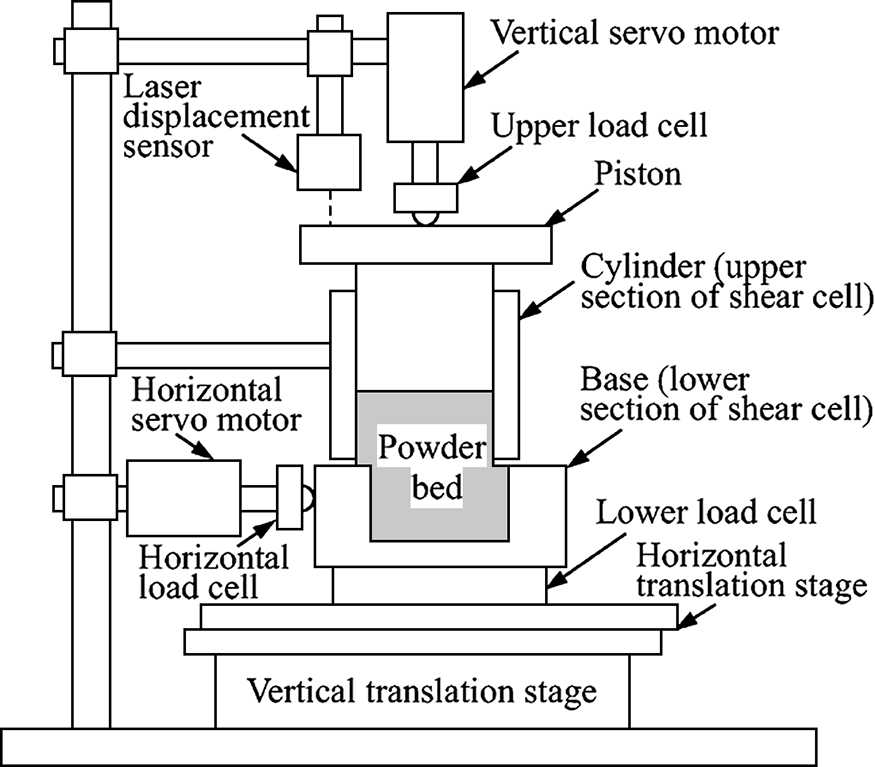
Constant volume tester. Reprinted from Shimada et al. (2018a) under the terms of the CC-BY-NC-ND 4.0 license. Copyright: (2018) The Authors, published by Elsevier B.V.

3.2 Rotational shear testers

Rotational testers overcome the restriction of a short shearing path employing a rotational force on two possible geometries: a circular path (Fig. 7a) or an annular path (Fig. 7b). In both, shearing is induced by rotation and the normal force is applied on the top. To shear the bulk powder, the lid and the base must rotate relative to each other. In most devices, this is achieved applying a torque, T, on the base while the lid is fixed, such as in the Schulze shear cell (Schulze, 1994). The reverse configuration, a fixed base and a rotating lid are used in testers like the FT4 (Freeman, 2007) and the Brookfield PTF (Berry et al., 2014). The surfaces of the base and the lid are roughened or equipped with blades to avoid sliding between the powder and the wall. The experimental procedure of rotational testers follows the same sequence: a pre-shearing step that conditions the sample, and a shearing test for every pair of normal and shear stresses to build the yield locus line. A rotational unit can apply an unlimited shearing path, and in this way perform multiple measurements on a single sample. It is easier to automate and therefore, reduces human error.

Fig. 7

Diagram of (a) torsional, (b) annular (ring) shear tester.

Many types of rotational testers can be found in literature, e.g. (Berry and Bradley, 2007; Bishop et al., 1971; Carr and Walker, 1968; Orband and Geldart, 1997; Schwedes, 1996). All operate under the same principles, and vary in their geometry, size, the range and the level of automation in the application of stress, and critically, in the sample preparation and the pre-shearing stage. Here, we will focus on describing three commercially available rotational testers: the Schulze shear cell, the Freeman FT4 shear tester and the Brookfield PTF, as representative examples of the design and the scope of the application of ring (Schulze and Brookfield) and torsional (FT4) units.

Fig. 8 describes qualitatively the experimental procedure. The Schulze shear cell (Schulze, 2008) is one of the first automated rotational shear devices. It features a rotating ring with a base that contains the sample, covered with a fixed annular lid where the normal force is applied. The inner surface of the ring and the lower side of the lid are roughened. Shearing is induced by rotating the bottom ring at angular velocity, ω, maintaining the lid stationary. To apply a normal force and rotation independently, the design includes additional elements, such as tie rods and a crossbeam used to stop the lid from moving. A normal force is exerted on the top and transmitted to the sample as the normal stress, σ. An upwards force counters the weight of the lid allowing the cell to operate under a small σ. The procedure is similar to that in Fig. 5b, but without the need to change the sample. It is faster and easier to automate. After the measurement of the first shear point (σ₁, τ₁), the sample is reconsolidated to σ_pr and sheared again to τ_pr (Fig. 8a). The normal stress, σ, is reduced, and the sample is sheared again to register the next point of the yield locus. Fig. 8b illustrates the experimental procedure in a Freeman FT4 shear tester (Freeman, 2007; Freeman et al., 2009). An FT4 shear cell is a torsional shear cell in a reverse configuration, whereby the base is stationary, and the shear is induced by a circular rotating lid (Fig. 7). The stainless-steel lid is fitted with 18 baffles of 2 mm in height to ensure that the shearing occurs only between the grains. The base is a cylindrical glass vessel plugged with a rough plastic cover on the base. The consolidation stress is applied lowering the lid onto the sample, and it is measured at the bottom. Once the desired value, σ_pr, is reached, the cell is rotated at very low speed, and the torque is recorded continuously. The procedure is the same, but the pre-shearing is different. The consolidated sample at σ_pr is sheared to the failure point in consecutive pre-shearing steps until the maximum shear stress, τ_pr, registered in each step remains constant (< 1 % difference - Blue - Fig. 8b). At this reference point, the first shearing test is performed reducing σ and registering the τ required for the bed to fail. In this step, the axial position of the lid is kept constant, and τ is computed as the peak of the shear curve (Red - Fig. 8b). Shearing is repeated at a varying σ to complete the yield locus line using an intermediate pre-shearing state in between each measurement to recondition the powder to (σ_pr,τ_pr). Fig. 8c describes qualitatively the test in a Brookfield Powder Flow Tester PFT. A Brookfield unit is like a Schulze tester, an annular (ring) device, but arranged in a reverse configuration with a stationary base and a rotating lid. It follows an experimental procedure similar to an FT4 with a slightly different definition of τ_pr (Berry et al., 2014). The cell is made of a stainless-steel annular base and a bladed lid. The consolidation stress is applied lowering the lid and measured at the top of the device. The sample if consolidated at high stress, σ_pr, and sheared several times until reaching a steady-state (Blue - Fig. 8c). One of its particularities is that the yield locus line is constructed from low to high consolidation, starting from a measurement at the lowest stress, $\frac{1}{3}{\sigma }_{\text{pr}}$, followed by $\frac{1}{2}{\sigma }_{\text{pr}}$ and σ_pr.

Fig. 8

Examples of rotational cells. Qualitative illustration of the evolution of the shear stress during the experimental procedure to construct the yield locus in (a) Schulze ring shear cell, (b) Freeman FT4 powder shear cell, (c) Brookfield PFT.

Shear cells are used as standard for the evaluation of the flowability of industrial powders and study their stability during storage, a key attribute of formulated powders. In many cases, materials are complex matrices of crystalline and amorphous components that are prone to cake through adhesion, sintering, deliquescence and formation liquid and solid bridges. Shear cells provide a way to study the effect of particle properties and the environment in this process. For example, Deshmukh et al. (2019) reports a recent study using a Schulze cell as an in-vitro tool for oral processing of foods, but similar devices have been used for decades. Teunou and Fitzpatrick (1999) proposed a ring unit specifically designed to study foods and investigated how environmental conditions affect the flow of flour, tea and whey powders (Teunou et al., 1999). The cell was installed in a chamber with controlled relative humidity rH and T. As expected, an increase in either of the two leads to a reduction in the flowability. The effect of consolidation and storage time was studied in a Jenike type cell (Teunou and Fitzpatrick, 2000) providing the evolution of flow functions. Fitzpatrick et al. (2007) used a similar device to study the effects of formulation and storage time in dairy powders. Opaliński et al. (2012) designed another Jenike type shear tester to study moist food powder and similar works on the study of mixtures of coal and sawdust or biomass mixtures were reported by Chen et al. (2012) and Zulfiqar et al. (2006). Torsional units have also been shown flexible tools. Guo et al. (2015) and Chen et al. (2018) used the FT4 shear cell to study the flow of biomass and coal blends with and without a varying level of moisture. Crawford et al. (2016) used it to study the effect of pre-processing of biomass and Léonard and Abatzoglou (2010) to investigate lubricated and unlubricated pharmaceutical powders. The FT4 shear cell was also used by Leung et al. (2017) to investigate the flowability of pharmaceutical powders mainly driven by cohesion.

Although fundamental and comparative studies are less frequent, they can shed light into the local stress distributions and on how the particle level properties relate to the bulk behaviour. For instance, Zafar et al. (2015) used a Schulze shear cell to investigate the flowability of cohesive powders, and compared the results to characterisation techniques such as the ball indentation (Hassanpour and Ghadiri, 2007) that measures the hardness at a low consolidation, and the Sevilla Powder Tester (Castellanos et al., 2004). Louati (2016) and Louati et al. (2015; 2017), used a Schulze shear cell for a fundamental investigation of the impact of moisture and particles size on the flow of glass beads, and Hammerich et al. (2020) designed a modified ring cell to study liquid saturated sediments. Wang et al., (2016) proposed instead a new method to analyse data using the FT4 under different initial consolidation. They tested over 40 powders with four initial consolidation stress and proposed an empirical relation between the flow function and a dimensionless cohesion C* (C* = C⁄σ_pr) that separates the effects of initial consolidation stress and the testing device.

There are other available shear devices like the Anton Parr rheometer that uses impellers for shearing, the Peschl cell that modifies a standard ring shear cell, and other commercially available units like the Hosokawa Micron Powder Tester or GranuDrum. Many others well-known testers have been developed for specific applications in research laboratories, for example, the use of fluidised beds to measured tensile strength (Castellanos et al., 2004) or flowability (Girimonte et al., 2018), and the analysis of caking with direct or indirect measurements of unconfined yield strength in uniaxial compression testers, e.g. (Hassanpour and Ghadiri, 2007; Thakur et al., 2014).

From a more fundamental point of view, the use of visualisation techniques such as Magnetic Resonance Imaging (MRI) can reveal the transmission of stress in a quasi-static flow at a particle level. Commercial shear cells made of metal are not suitable, but novel shear testers have been designed for this specific purpose (Mueth et al., 2000). The work of Cheng et al. (2006) and Sakaie et al. (2008) reports a direct measurement of the evolution of the local packing of a slow and smooth granular shear flow in a split-bottomed geometry. They sheared MRI sensitive seeds at different rotational velocities and collected MR-images after stopping the shearing process. Börzsönyi et al. (2011) followed a similar approach to demonstrate that a shear zone develops preferentially in regions with a lower friction. They studied a U-shaped horizontal shear cell consisting of two parallel L-shaped sliders and characterised the shearing band recording the displacement of MRI-sensitive poppy seeds loaded in a sample of MRI-insensitive glass beads.

Classic or new devices and commercial and custom designs, all shear cells work under the same principle. And yet, different dimensions, sample volume and pre-shearing procedures lead to disparities in the measurements from different testers. The impact the history of a powder has in its response to stress is well documented (Swize et al., 2019), but the sample preparation procedures are still specific to each device. The work of Berry et al. (2014) and Salehi et al. (2017a) compares the measurements of Brookfield, Schulze and Jenike testers, and Koynov et al. (2015) reports on a comparative study of shear cells evaluating the flow of coarse (59 mm) and fine (4 mm) alumina powder. Salehi et al. (2017a) found no important disparities between testers, the largest differences being ascribed to highly compressible powders, but the observations of Berry et al. (2014) were consistent with the issues listed by Koynov et al. (2015). In their comparative work, all shear cells provided a good qualitative measurement of flowability, but they were found to be more efficient with fine, cohesive powders. In free-flowing powders, measurements could not be used in a quantitative way to rank the materials but only to identify them as free-flowing. Comparison across different cells showed that not only the consolidation stress during pre-shearing is important, but also the type of shear cell. Barletta et al. (2015) provided a similar comparative analysis in the context of biomass and identified important differences only in the wall friction coefficients. It is in line with the work of García-Triñanes et al. (2019), which finds minor differences in the measurement of tensile strength of cohesive powders in a Schulze and a Brookfield unit.

The full range of available devices to characterise the quasi-static flow of complex cohesive mixtures is described by Ghadiri et al. (2020), Ogata (2019), and Schwedes (2003). Here we provided the reader with an overview of the design of classic shear testers, their limitations and their scope for application. In the following sections, we describe how the modification of the classic designs with the use of aeration and other external sources of actuation can lead to a new type of devices that are capable of performing measurements in an intermediate regime and providing a more complete picture of the granular rheology.

4. Beyond the quasi-static regime

In the quasi-static regime, the yield locus line describes the failure of a network of enduring contacts between particles in a bed of powder. Under an applied normal stress, σ, the required shear stress τ = μ σ + C is purely a function of the bulk material properties and the structure of the sample created by the consolidation at (σ_pr, τ_pr). However, at higher shear rate, or lower consolidation stresses, the powder dilates, and as it transitions into an intermediate regime, the shear stress, τ, establishes a dependency on the shear rate, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$. There are several ways to try to replicate and characterise this transition in a modified shear cell. In order to depart from the quasi-static regime, one must operate at a higher inertial number, I, (see Eq. 1) by either operating at a sufficiently high shear rate, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, or at a sufficiently low (constant) consolidation stress, σ.

The operation at $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ simply by operating at a high rotational speed in indeed possible (Bagnold, 1954) but in practice this can lead to attrition of fragile particles. Ghadiri et al. (2000) discuss in detail the importance of breakage and segregation in a annular cells using catalyst powder, and Hare et al. (2011) provide an example where measurements of the attrition of pharmaceutical powders in a shear cell are coupled with computational studies in an agitated bed.

Alternatively, the inertial number, I, can be reduced operating at low consolidation stress, σ. Doing so requires the application of an energy source to the bed that can overcome the action of the gravitational acceleration that would otherwise consolidate the sample. The additional energy input can be introduced by the action of a particle-fluid force using aeration or even complete fluidisation, or through mechanical acceleration, such as agitation or vibration of the sample. The following sections provide a summary of current strategies describing a selection of shear devices that use an external actuation to operate at low consolidation stresses. Modified classic shear cells are introduced in Section 4.1, and Sections 4.2 and 4.3 describe the design of Couette-type rheometers and the use of mechanically agitated aerated or fluidised beds.

4.1 Modified shear testers

One of the first modified shear testers was introduced by Klein et al. (2003). They developed an annular (ring) cell to shear a limestone powder (d_p < 15 μm) at varying normal stress and a shear velocity between 0.07 to 4,200 mm/min. The design resembles a Schulze tester with the functionality of powder aeration. A motor is fixed to the base to rotate the shear cell at the desired velocity. The base and the lid are made of a permeable material, and feature 24 thin baffles to prevent the sample from sliding during the shearing process. The vertical normal stress, σ, is applied by the lid on the top of the sample. Aeration is modulated via a mass flow controller or through the measurement of air pressure in the exhaust. A fluidisation index, FI, is defined as ratio between the pressure drop of the gas flowing through a bed of powder ΔP, and the pressure drop required to counter the weight of the bed and reach the minimum fluidisation, ΔP_mf = W⁄A. Or in other words, the ratio between the gas superficial velocity, u_g, and the minimum fluidisation velocity, u_mf, FI = ΔP⁄ΔP_mf~u⁄u_mf. When particles are aerated by a gas velocity lower than u_mf, FI < 1, the bed of powder remains static but it sustains much lower normal stress, σ, due to the reduction of its effective weight under the action of a drag and buoyancy forces. Klein et al. (2003) studied the effect of aeration in the rheology of limestone. They observed no differences in the shear stress, τ, required for the bed to fail under a constant normal stress, σ, and a fluidisation index FI < 0.7, in an indication that the powder remains in a quasi-static regime. However, under a higher FI but still operating with a fixed bed, 0.7 < FI < 1, the shear stress, τ, was found to decrease for an increasing air velocity indicating the presence of an intermediate regime between the quasi-static and the collisional regime characteristic of a fully fluidised system at FI ≫ 1.

Another example of a classic tester with an aeration functionality was proposed by Johanson and Barletta (2004). They modified a Schulze device, to operate under a continuous counter air flow using a base of permeable media and a modified perforated lid. Air pressure was measured at the inlet and the flow was controlled with a rotameter. They performed shear experiments on a fine silica powder (d_p = 8 μm) and an FCC catalyst (d_p = 50 μm) and with a range of aeration up to FI = 1. As expected, the unconfined yield strength of the bulk material was found to decrease with increasing aeration. The effective angle of internal friction decreased approaching full fluidisation. Other modified testers include the device developed by Barletta et al. (2007), which coupled a circular cell with the rotating plate of a Peschl shear test bench to investigate the effect of aeration in the flow of fine silica (d_p = 7.6 μm) and magnesium carbonate (d_p = 3.5 μm). The design resembles that of a short FT4 rheometer, featuring a circular fixed base and a bladed rotational lid. The base is 61.8 mm in inner diameter and 15 mm in height, and it consists of a porous bottom plate that ensures a homogeneous air distribution. The experimental procedure mimics that of Fig. 8b. Experiments were performed at low shear rates, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, and normal stress, σ, and below the minimum fluidisation (FI < 1). Their results confirm the observations of Klein et al. (2003): for a fluidisation index FI < 0.7 no significant differences appear in the angle of internal friction, in an indication that even when aerated, the samples remained in the quasi-static regime.

4.2 Couette-type shear testers

Annular cells are a classic arrangement to study the rheology of Newtonian and non-Newtonian flows (Viswanath et al., 2007). Fig. 9a provides a generic description of the geometry. In these devices, the fluid is sheared in between two coaxial cylinders: an inner rotating one called bob and an external steady cylinder called cup. The viscosity and the shear stress are computed from the angular velocity, ω, and the torque, T, applied to the inner cylinder. Couette-type shear testers have been often used to study granular flows. Interested readers are referred to the overview by GDR Midi (Midi, 2004) for characteristic experimental velocity profiles. The evolution of the bulk or effective friction coefficient μ_b in a Couette cell is given as a function of a dimensionless characteristic shear rate, ${\widehat{\dot{\gamma }}}_C={\dot{\gamma }}_{\text{w}}\sqrt{d/g}$, where ${\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}}_{\text{w}}$ is the shear rate at the wall. The use of ${\widehat{\dot{\gamma }}}_{\text{C}}$ is a particular case of the general inertial number I (see Eq. 1) that considers a hydrostatic pressure as the source of the consolidation stress. Experimental velocity profiles in Couette cells show the existence of localised shear bands on the wall of the rotating cylinder that depend on the conditions of the boundaries. In order to avoid sliding, the walls of the cylinders must be roughened mechanically or by glueing particles or sandpaper. Due to the simplicity in design and control, Couette cells are an excellent alternative to study the intermediate flow regime. The type of geometry described in Fig. 9a has been used for a long time to study powders and capture the stress–strain rate relationship (Craig et al., 1986; Hanes and Inman, 1985; Savage and Sayed, 1984). Modern devices without any actuation include the units proposed by Tardos et al. (1998) and a shorter, annular device described by Klausner et al. (2000). Every cell imposes a fixed shear rate and relies on the action of gravitational acceleration to consolidate the sample. The earlier studies establish a dependency of the shear stress on the shear rate that simply by operating at high shear rate, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, increasing the rotational speed of the inner cylinder, and thus ${\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}}_{\text{w}}$. The boundaries for the transition from the quasi-static to the intermediate regime and inertial regimes are still under debate. Experimental values have been proposed by Tardos et al. (1998; 2003) for the departure of the quasi-static regime, i.e. ${\widehat{\dot{\gamma }}}_{\text{C}}~0.15/0.25$, and the collisional regime ${\widehat{\dot{\gamma }}}_{\text{C}}~3$, and later confirmed in computational studies (Vidyapati et al., 2012). In order to achieve a more general description and reach a higher range of inertial numbers, I, one can also reduce the consolidation stress, σ, linked to the powder weight. In the following sections, we describe the design of Couette cells that introduce aeration or flow in a coaxial-cylinder configuration, Section 4.2.1, and virtual cells that minimise sliding effects, Section 4.2.2.

Fig. 9

Depiction of a generic geometry of a (a) Coaxial-Cylinder rheometer applied to powders, and its use within a (b) flow and (c) aerated device. Nomenclature: R_i and R_e: inner and outer radii, L: bed height subject to shear; ω: rotational speed.

4.2.1 Aerated coaxial-cylinder rheometers

Two alternatives have been proposed in literature in order to actuate a coaxial cylinder rheometer (Fig. 9a) and operate at higher inertial numbers. One can impose an axial particle flow in the annular section inserting the unit in flow device (Fig. 9b) or inject a counter-current stream of air to reduce the consolidation stress in an aerated or fluidised chamber (Fig. 9c).

Tardos et al. (1998) first used a coaxial cylinder rheometer to investigate shear stress of non-aerated and aerated powders. Its geometry and operation conditions are listed in Table 1. The unit featured two concentrically placed cylinders and the possibility to aerate the bed. The walls of both cylinders were covered with sandpaper to minimise sliding. Two sets of experiments with and without aeration were performed to study the effects of torque and the height of the powder bed on the stress evolution. The experiments under aeration (0 < FI < 1) investigated the distribution of stress under a varying shear rate. Fine free-flowing dry powders were tested at three rotational speeds, ω, and three bed heights, L. The authors proposed a model for the variation of the torque, T, based on the assumption of a linear hydrostatic granular pressure, as:

Table 1

Summary of aerated or vibrated Couette-type cells for the characterisation of intermediate granular flow.

Reference	Material	FI	dp [μm]	ω [rpm]	$\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ [s−1]	Re / Ri / r* [mm]	L [mm]
r1: Anjaneyulu et al. (1995)	Glass	>1	400–900	150	0.07/1.65	32.5/6–11	20–40
r2: Tardos et al. (1998)	Multiple	0–1	70–530	20/250	10/120	76.2/63.5	195–285
r3: Marchal et al. (2009)	Glass	Vibrated	530	—	10−6–102	20/10/11.5	30
r4: Colafigli et al. (2009)	Silica	>1	26	2.4/16	0.12/0.76	69/50	300
r5: Langroudi et al. (2010a)	Glass	Flow	500–1000	5/60	0.25/9	152.4/101.6	101.6–406.4
r6: Landi et al. (2012)	Glass	>1	48	3	0.13	69/50	300
r7: Gutam et al. (2013)	Multiple	0	830–1300	—	0.34–1.7	75/35–60	190
r8: Lupo et al. (2019)	Multiple	0>1	80–266	0.5	—	25/10.5	28
r9: Yahia et al. (2020)	Glass	0–1	50–500	8/180	2.75/22	70/10–18/12–20	70

  

$$T=(\tau R)2\pi RL=\pi {\rho }_{\text{b}}\hspace{0.17em}g{L}^2{R}_{\text{i}}^2\text{sin}(\mu )\left[1-\frac{u_{\text{g}}}{u_{\text{mf}}}\right]$$(3)

Here, ρ_b is the bulk density of the powder and the last term accounts for the effect of the superficial velocity in reducing the effective weight of the sample. Eq (3) predicts a linear dependency of the shear stress with the bed height, τ~L, and a linear dependency between of the torque with the gas velocity, T~u_g, but a quadratic dependence of the torque with the radius of the rotating cylinder, $T~R_{\text{i}}^2$, and the height of the powder bed, T~L². The authors assessed the validity of Eq. (3) through experimental measurements of the stress distribution in a stationary material. Unlike Eq (3), the well-known Janssen equation describes an exponential distribution of the stress across the depth, but it would predict a linear dependency, T~L, for a powder in a quasi-static regime when the normal stress reaches an asymptotic value below a certain depth. The experimental results obtained across different particle densities, diameters, shear rates and aeration levels confirmed the prediction of Eq. (3) based on hydrostatic loads and the effect of aeration in reducing σ. These experiments were operated at low shear rates, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, and the results did not show any relation between T and $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$. In a further series of experiments, Tardos et al. (1998) investigated the effect of higher shear rates (or higher ${\widehat{\dot{\gamma }}}_{\text{C}}$) increasing the rotational speed to 250 rpm bulk samples of non-aerated coarse glass beads. The effect of the hydrostatic load was studied placing an 8 cm high layer of powder on top of the shearing column that blocked the bed from expanding. The results using different geometries showed a weak dependency of the dimensionless torque and shear rate ascribed to the variation of the annular gap that was actually sheared. However, in the configuration with an additional layer of powder, the entire annular gap was sheared, and a linear correlation appeared between the dimensionless torque and shear rate with a slope of 0.25. This is one of the first studies capturing the departure from a quasi-static flow and two distinct behaviours: quasi-static at a low shear rate and intermediate at higher shear rate.

The same linear relationship between the stresses and the height was confirmed across a broader set of experiments by Tardos et al. (2003) varying the size of the internal cylinder, and including measurements of normal stresses in the radial and axial directions with the use of piezoelectric sensors. In this work, a new constitutive equation was proposed to unify quasi-static, intermediate and inertial regimes on the basis of a 2D analysis of the Couette flow using the additive approach of the stresses of Savage (1998).

Langroudi et al. (2010a; 2010b) were the first to propose the creation of a flow system to increase the inertial number in a coaxial-cylinder chamber. Fig. 9b depicts the general concept. These units offer some flexibility. They can be operated either in a batch or under a continuous axial flow of material in the annular space. The height of powder in the shearing band can be controlled with the powder flow rate, and an additional layer can be maintained above the shearing band, denoted overburden, to control the consolidation. In the study of Langroudi et al. (2010a; 2010b), the behaviour of coarse glass beads was evaluated first without the presence of the overburden. Four bed heights, L, and four rotational speeds were tested. As described by others in aerated (Tardos et al., 1998) and fluidised devices (Anjaneyulu and Khakhar, 1995), shearing caused the stratification of the flow with two distinct layers of mobile and stagnant powder. Analysis of the torque was in agreement with Tardos et al. (1998) and confirmed the linear correlation between τ and the bed height, L. The analysis confirmed the presence of two regimes, a quasi-static flow at low shear rates where τ is independent of $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, and an intermediate at higher values where τ increases with increasing $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$. The authors assumed a power-law for the stress and shear rate relation, $\tau ={\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}}^n$, and found that the n-index ranges from 0.5 to 1 and increasing with higher shear rate. This work provided also important additional information by measuring the normal stress, σ, acting on the shearing surface of the material. Stress sensors were placed in both the surface of the outer and inner cylinders, and a further set of experiments was conducted with a fixed bed height at 406.6 mm, an overburden of 101.6 mm and increasing ω from 5 to 60 rpm. As expected, the normal stress σ measured at the wall increased linearly with the depth in the powder bed, and it was independent on the rotational speed, ω. Measuring both the shear stress (indirectly) and the normal stress (directly), they estimated the angle of internal friction, μ, and found that it was comparable to the one evaluated with classic shear testers at low $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$. The authors proposed a constitutive model based on the data that blends the Coulomb yield condition at zero shear with a power law at a higher shear rate, $\tau /\sigma =\tan \left(\mu \right)+b{\left|\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}\right|}^{}$. In a later study, Langroudi et al. (2011) used the same device equipped with capacitance probes to study the effect of polydispersity and shape in secondary flow patterns and the powder dilation.

Langroudi et al. (2010a) also studied the effects of the bed height, L, without overburden and confirmed a linear dependency of the average τ on L with a slope proportional to γ̇. However, as pointed out by Ghadiri et al. (2020), there have been conflicting experimental observations. Mehandia et al. (2012) and Gutam et al. (2013) report evidence of an exponential behaviour studying in detail the axial distribution of the stress in slow regime on a similar arrangement (Table 1) including the direct measurement of radial and axial normal stresses. In their device, aeration was used only to homogenise the bed of powder, and the samples were pre-sheared during 20–30 min to remove any history effect. In contradiction with the observation of Tardos et al. (1998; 2003), all components of the stress tensor were seen to increase exponentially with the depth in the bed. The behaviour was found to be consistent with the Janssen equation across a range of conditions, which was ascribed to the inherent anisotropy of the bed fabric. In a later work, Krishnaraj and Nott (2016) associated the abnormal quadratic dependence of the stress with depth to the formation of a secondary vortex in a Couette geometry. The authors argue that the gravitational acceleration and its interplay with the confinement are responsible of causing a deviation from the expected liquid-like behaviour in isotropic plasticity models. These models disregard the transmission of stress to a boundary as the majority of computational DEM works do by imposing Lees Edwards boundary conditions. The role of geometrical constraints, particularly the size of the annular gap, therefore, requires further investigation.

Lupo et al. (2019) conducted a similar study using an Anton Paar cell featuring a pseudo-cylindrical impeller with a grooved surface. They carried out torque measurements on aerated and non-aerated samples by immersing the impeller at various bed depths. Experiments were performed below and above the minimum fluidisation using different powders (see Table 1). As expected, T decreased with the depth of the impeller for all the cases studied and decreased with increasing gas velocity. However, the more complex geometry of the cylinder/impeller requires further analysis to be able to compute the stresses.

Couette flow configurations have also used to investigate higher levels of aeration. For example, Anjaneyulu and Khakhar (1995) introduced an adapted Coaxial-cylinder rheometer to study of the rheology of a fluidised beds following an aerated arrangement, Fig. 9c. A viscometer (Brookfield, Synchro-Lectricas) was used to rotate an inner cylinder. Two geometries with varying internal radius were tested using glass beads with various sizes and reaching complete fluidisation FI > 1 (Table 1). For each airflow, the inner rotating cylinder was immersed in the glass beads sample at different elevations L. The experiments showed the formation of a dynamic layer around the rotating cylinder and a static layer at the vicinity of the wall. In line with this observation, the authors proposed a pseudo-plastic constitutive equation based to describe the granular material as a Bingham fluid. Fitting the experimental results led to estimates of the bulk shear viscosity, μ, and the yield stress, τ_y, where τ_y defined as the shear stress at a very low rotational speed (ω→0). As expected, both μ and τ_y, decreased with increasing air velocity, but while τ_y decreased monotonically and beyond the fluidisation conditions, μ reached nearly constant value for FI > 1. This behaviour was explained by the motion of the gas from the sheared inner region to the outer packed region. The yield stress, dominated by the outer packed bed, decrease as more gas flows through for a higher FI but the viscosity, μ, remains constant since it is governed by the shearing of the rotating inner region, which does not dilate further. Both μ and τ_y were found to be independent of the particle size for the same FI. At a low aeration level, the experimental results were more scattered, and the inner cylinder radius and the immersion depth had a significant effect on μ and τ_y.

Colafigli et al. (2009) developed an alternative design for high aeration levels, known as the Couette Fluidised-Bed Rheometer (CFBR). A CFBR is designed to measure the apparent viscosity in a homogenous gas-fluidised bed. It features the same type of aerated geometry, Fig. 9c. The external cylinder was made of Pyrex to allow direct observation of the fluidisation dynamics, and the inner cylinder was made of stainless steel. Colafigli et al. (2009) used nitrogen at ambient conditions as the fluidisation medium and silica powder (d_p = 26 μm). The height of the bed was maintained at a constant value to have the inner rotating cylinder fully immersed, and enough space was left above the bed to accommodate the expansion of the bed. The apparent viscosity was evaluated from the steady-state value of the torque assuming a laminar flow in the annular gap. The values of viscosity were computed with the assumption of a Newtonian fluid and, therefore, they provide only an estimate of an “apparent” viscosity. Nonetheless, the results indicated a clear and significant decrease in the mean apparent viscosity with increasing ω. For a fixed rotational speed, the mean apparent viscosity decreased with increasing airflow. Despite it remains unclear how to convert the registered torque, T, to bulk physical properties such as viscosity or yield stress, CFBRs offer an easy way to evaluate and compare different powders and even study the effects linked to changes in particle properties or operation conditions, e.g. temperature or pressure. For example, Landi et al. (2012) used a CFBR to investigate the flow properties of moisturised glass beads with relative humidity rH ranging from 15 % to 70 %. In this work, the rH was controlled by using pre-humidified air stream used as a carrier in the bed. Surprisingly, the minimum fluidisation velocity (0.09–0.12 m.s⁻¹) followed no apparent trend with the rH, and at a fixed rotational speed (Table 1) the torque, T, was found to decrease monotonically with superficial gas velocity, independently of the value of the rH.

A better understanding of the development of the flow and the force chains in a Couette device can be obtained with visualisation techniques such as magnetic resonance imaging (MRI). For example, Moucheront et al. (2010) reported an MRI investigation of granular rheology in a Couette device similar to that in Fig. 9a, where the material (Mustard seeds-MRI sensitive) was confined between two plastic cylinders and sheared by the rotation of the inner one. Multi-layer MRI velocimetry was used to evaluate the velocity profiles at different elevations. The authors were able to determine the effect of the roughness of the inner cylinder and the bottom base on the flow structure. The results demonstrate that the roughness of the bottom surface has an effect localised only to a few granular layers, but the roughness of the inner cylinder wall affects significantly the system determining the sliding velocity and the friction coefficient.

4.2.2 Aerated virtual Couette configurations

The error associated with the roughness of the boundaries and the reliable estimation of shear stress τ are some of the challenges encountered by coaxial-cylinder rheometers. New modified cells address some of these issues proposing new ways to harmonise the experimental data and the wall boundary conditions. A coaxial-cylinder rheometer can be easily modified by replacing the inner cylinder by an impeller while maintaining a Couette flow. The resulting alternative design is called virtual Couette flow. It is depicted in Fig. 10. It has been used in the study of granular material by several authors including Marchal et al. (2009) and Yahia et al. (2020). Both studies used the same strategy: the inner cylinder is replaced by an impeller with a longitudinal arrangement of equidistant straight baffles aligned with the radial direction, see Fig. 10b. The inner element rotates at a fixed position inside the material. In doing so, the impeller creates a cylindrical geometry filled with powder under solid body rotation at the velocity of the baffles. A shearing plane is created exclusively between granules at the outer surface of the moving virtual cylinder, therefore eliminating any potential sliding effects.

Fig. 10

Virtual Couette Flow: (a) Schematic, L: cell height; ω: rotational speed, R_e, R_i and r*: external, inner and optimal radii; (b) Image of the impeller denoted virtual cell. Adapted from Yahia et al. (2020) under the terms of the CC-BY 4.0 license. Copyright: (2020) The Authors, published by Wiley Periodicals, Inc.

Marchal et al. (2009) used a virtual Couette cell to investigate the effects of mechanical vibration on granular rheology. They first introduced the definition of an optimal radial position, r*, (see Fig. 10a) as a way to translate the torque measurement into a transportable measurement of shear rate, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, and stress, τ. The optimal radial position, r*, is an exclusive geometrical property of each Couette configuration. When reported at r*, both τ and $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ become independent of the dimensions of the outer and inner cylinder. The formulation of r* was confirmed with further experimentation with Newtonian and non-Newtonian fluids by Aït-Kadi et al. (2002) where several Couette-type flow configurations were tested. This is a critical step in order to fix a standard procedure to report data. Marchal et al. (2009) employed an inner cylinder made of stainless steel. The baffle width was 5 mm and six were glued also on the external cylinder surface to avoid particles sliding. The external cylinder was mounted on a plate to apply mechanical vibration during the shearing process. Experiments were performed with and without vibration using a sample of coarse glass beads and a varying the shear rate, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ (Table 1). The results obtained in a non-vibrated bed found no stress-strain rate relationship, but under mechanical vibration and low values of $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ the shear stress, τ, and the shear rate, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, were found to be linearly proportional describing a Newtonian behaviour.

A more advanced design including aeration, called an Aerated Bed Virtual Couette Rheometer (AB-VCR) was proposed by (Yahia et al., 2020). The AB-VCR adapts a virtual Couette geometry similar to the one presented in Fig. 10 to the FT4 Powder Rheometer. The aerated vessel of the FT4 is a glass cylinder. The inner cylindrical element (so-called virtual cell) has 3D printed six blades made of plastic material (ABS-M30i, SYS systems 3D Printing). Yahia et al. (2020) conducted experiments with and without aeration.

Under no aeration, the shear stress, τ, was found to be independent of shear rate, $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, indicating that the powders were in the quasi-static regime. At a fixed value of $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$, the shear stress, τ, was dependent on particle size, which was ascribed to different bulk internal friction of each size class (μ_500μm = 0.46 + 0.02, μ_50–80μm = 0.36 + 0.01, μ_160–210μm = 0.32 + 0.01). The bulk friction coefficient measurements were compared with FT4 torsional shear cell experiments, and they showed very good agreement. During the aeration experiments, ambient air was injected through the sample using a stainless-steel base grid to have a homogeneous flow distribution. The air velocity was increased from no aeration to a fluidisation index FI < 0.4, at a varying shear rate $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ (Table 1). All powders display a quasi-static behaviour under this range of aeration. The shear stress, however, was found to decrease with the increasing air velocity in agreement with the observation of Tardos et al. (1998). It is worth noting that unlike them, this work operated only in a batch mode and did not study the effect of an additional static layer of powder atop of the sample to prevent the expansion of the bed. For a fixed fluidisation index, a good agreement was found between the results obtained with samples with the same angle of internal friction, μ, while the shear stress, τ, associated with a higher μ was systematically lower. Yahia et al. (2020) demonstrated the potential of r* to standardise the measurements in Couette shear testers. The authors compared the use of three virtual cells of a varying radius and a fixed bed height (Table 1). As expected, in every powder, the torque, T, depended on the dimensions of the virtual cell, increasing for an increasing radius. However, the shear stress τ computed at the optimal position, r*, using the recorded torque, T, was the same for all the cells used.

These devices are still in development and quantitative comparison is necessary, but the selection of presented here shows the potential of Couette cells to investigate the departure from a quasi-static flow. The versatility of the device permits to operate at a wide range of rotational speeds, with or without an overload of static powder, with and without aeration, vibration or an imposed gravitational flow, and they allow varying the geometry with a sound scaling parameter. However, the computation of τ from T in each historical work is based on different assumptions, and the complete of information necessary to reconstruct it is missing from most of the studied. Not all of them operate under the free expansion of the bed, a wide range of particle properties and geometries is present, and the nature of the axial distribution of stress remains to be clarified. Nevertheless, the use of the optimal radial position, r*, opens the way to establish a standard in the computation of the shear stress and the shear rate. At this point, a comparative analysis of the studies in Couette configurations is limited to the qualitative features summarised in Table 2. Overall, experiments find the expected behaviour at low $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ where τ is independent of $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ with and without aeration. As $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$ increases at a high FI aerated cells capture the departure from a quasi-static regime, whereby τ starts to increase for increasing $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\gamma <!--\; \gamma \; -->}}$. This relation is modified with the operating γ̇ and the level of aeration. The torque and the bulk viscosity decrease with the superficial gas velocity, and there are conflicting reports regarding the axial distribution of the stress, where both a linear and an exponential dependency with the bed height have been suggested.

Table 2

Summary of the experimental behaviour described in the cells listed in Table 1.

Reference vs. main experimental observation
r1	Adopts Bingham model; μ and τy decrease with ug
r2	Measures T and deduces a hydrostatic stress profile (σ~L). Captures intermediate flow for ${\widehat{\dot{\gamma }}}_{\text{C}}>0.15$
r3	Proposes a vibrated virtual cell and r*. Finds Newtonian behaviour τ ~ γ̇ under vibration and low γ̇.
r4	Adopts Newtonian model; μ decreases with ω
r5	Measures normal stresses consistent with a hydrostatic stress profile (σ~L); finds τ / σ = tan (μ) b |γ˙|0.72
r6	Measures T decreases with ug independently of rH.
r7	Measures normal stresses in agreement with Jensen Eq and in contradiction with a hydrostatic stress profile.
r8	Measures how T decreases with L and ug
r9	Demonstrates the use of r* in an aerated virtual cell; finds that τ decreases with ug in quasi-static regime.

4.3 Mechanically stirred (agitated) beds

Mechanically stirred beds are used to study the highest range of shear rates under complete fluidisation. They measure the torque, T, required to rotate an impeller immersed in a powder bed, Fig. 11a. T depends on the structure of the powder and reflects its flowability. Depending on the impeller shape and its position in the bed, T could be used to compute a characteristic shear stress, τ. For example, Bruni et al. (2005; 2007) developed a mechanically stirred fluid-bed rheometer (msFBR) consisting of a flat impeller (36 mm diameter × 7 mm height × 0.7 mm thickness) that rotates at a fixed position inside an aerated bed. The test was conducted varying the impeller depth and the rate of aeration below and above the minimum fluidisation. The powder was preconditioned in every test by fully fluidising it and decreasing the aeration level to the desired value to remove any history effects. Bruni et al. (2005) explored the effect of the aeration rate (0 < FI ≤ 1), the impeller speed (0 to 8.79 rpm) and the depth ID on the torque, T, using alumina and soda glass beads. Under aeration, FI < 1, the torque, T, was found to reach a constant value at each speed only after a sufficiently long time, and as expected, it increased with the depth until reaching a plateau at the bottom end. In a later work, Bruni et al., (2007) proposed a model based on the Janssen equation and the Mohr–Coulomb yield criteria to predict the stress at the impeller depth, and evaluate the change in T at low consolidation resulting from the combined action of the sample weight, the aeration and the impeller position. This work studied alumina powders and glass beads varying the position of the impeller with or without aeration (FI < 1), and concluded that independently of the impeller depth, the aeration does not influence T. Tomasetta et al. (2012) estimated the flow properties from the data reported by Bruni et al. (2007) developing a new procedure to compute the shear stress, τ, and the consolidation stress, σ, from the torque. τ was found to increase linearly with σ in a similar way to the yield locus characteristic a shear tester. The bulk friction coefficient, μ_b, was then simply computed by τ/σ. It was shown that the computed values of μ_b were in a good agreement with the measurements obtained in a Schulze ring shear test.

Fig. 11

Examples of stirred aerated/fluidised beds: (a) Depiction of the generic geometry (b) Qualitative evolution of the BFE with increasing gas superficial velocity, u_g, during a FT4 downwards test.

The FT4 rheometer can also be used as a mechanically stirred aerated bed. The unit is equipped with a twisted stainless-steel rotated blade that moves downwards and upwards through the powder. As in all the FT4 tests, the powder is prepared in a conditioning cycle where the twisted blade moves through the sample rotating in a clockwise direction, creating a uniform, reproducible lightly packed sample (Freeman, 2007). Two tests can be performed with a mechanically stirred configuration: downwards and upwards. In both, the blade rotates in an anticlockwise direction. In a downwards test, the rotation of a twisted blade results in shearing while the axial movement applies a normal stress to the bed. The torque and the vertical force recorded in a downwards test can be used to derive a so-called Basic Flowability Energy (BFE) which represents the energy required for the blade to complete a full translation. The BFE is, therefore, a parameter specific to the FT4. It lacks universal meaning, but it allows a direct comparison of the flowability of different powders at various aeration conditions. Fig. 11b illustrates the typical evolution of BFE with superficial gas velocity u_g. A non-dimensional aeration ratio (AR) defined as the ratio of BFE at no aeration to BFE at a given air velocity has been proposed as a way to classify flowability. If AR ~ 1 the powder is not sensitive to aeration, which is typical of very cohesive powders or a higher binder content. If AR >> 20, the powder displays a low cohesive strength, it is very sensitive to aeration and likely to be fluidised. There are many examples where the FT4 aeration test has been able to rank the flowability of powders (Freeman, 2007). For example, Gnagne et al. (2017) reported the properties of flours, Ono and Yonemochi (2020) studied the effect of additives in the flowability of ibuprofen and Ludwig et al. (2020) evaluated its behaviour under fluidisation.

Although the method is clearly able to rank powders, it does not provide a transportable set of properties. The complex geometry of the blade makes it difficult to evaluate the characteristic strain rate and the shear stress, but the combination of experimental and computational studies can help to address some of these limitations. The work of Hare et al. (2015; 2017) suggests that it is indeed possible to determine a characteristic τ for a powder in the FT4 aeration test. Hare et al. (2015; 2017) combined experiments and DEM simulations to determine the shear stress profile in the bed. In order to estimate the strain rate and shear stress they analysed the dynamic behaviour of a bed of large cohesive glass beads (d_p = 1.7–2.1 mm) during the FT4 aeration test and found that τ was be constant across the blade length and increased as the impeller penetrated the bed. Hare et al. (2017) later provided a similar framework to analyse the stress and strain rates, and Nan et al. (2017a; 2017b) combined computational and experimental work to study how aeration and shape affected the stress profiles in samples of soap roads, polyethylene and glass beads.

Oher commercially available stirred beds include the Anton Paar Powder Cell (APPC). This device works with the same principle as the msFBR (Bruni et al., 2005; 2007) recording the torque acting on an impeller immersed in an aerated powder bed. The bed can be operated either below or above the minimum fluidisation. The cell containing the powder is made of a glass cylinder with a porous bottom plate, and the unit is equipped with impellers of different shapes and wall conditions. Salehi et al. (2017b) used an APPC to study the effects of the impeller depth and the aeration rate on the torque acting on a flat blade impeller in samples of free-flowing powders, namely glass beads, alumina and sieved silica sand, up to the minimum fluidisation (0 < FI < 1). The dependency of T on the air velocity, the bed height and the impeller depth confirm the observations of Bruni et al. (2005; 2007). They proposed to use a fitting parameter as the “effectiveness” of the impeller to estimate T at different depths. The model is based on the assumption that the shearing occurs only within the cylindrical region captured by the impeller rotation. In a later work, Salehi et al. (2018) measured T under different geometries in non-aerated glass beads of different sizes. In a similar fashion to the works in an FT4, a combination of computational and experimental data was used to evaluate internal flow parameters such as the bulk friction coefficient between particles and between particles and the blade.

5. Conclusions

Classic shear cell devices and a broad array of ad-hoc experimental tests have served for decades as the standard to evaluate the flow threshold of cohesive industrial powders. However, looking only at the initiation of the flow is a rather simplistic view of the rheology of granular materials. It fails to capture their dynamic behaviour and the transition to intermediate and inertial regimes. These are fundamental aspects of the flow behaviour observed in natural systems and industrial units. In order to efficiently process powder, optimise unit operations and develop new technologies involving dense particle flows such as process, energy and additive manufacturing, one requires a precise understanding of all granular flow regimes. Dynamic tests and many flow configurations have been proposed as alternative ways to characterise the dynamic behaviour of a powder. However, even the simplest devices such as rotating drums, chutes or avalanches display a very complex flow pattern, and the resulting bulk properties are difficult to interpret.

It is important to move towards establishing a rigorous and transportable analysis of the data across different devices. This review provides an overview of the strategies developed in recent years to expand the usage of conventional shear cells from the quasi-static regime into the characterisation of intermediate and inertial flows by applying external actuation. However, the practical difficulties in operating at higher shear rates and the complex behaviour of granular matter make the development of flexible instruments very difficult. Commercially available units such as the FT4 rheometer or the Anton Parr Powder Cell have tackled this challenge using a rotational cell under aeration to achieve very small consolidation stresses. Many other customised devices have followed similar principles using modified testers, flow devices, fluidised bed rheometers and mechanically agitated beds. The main drawback of these units is linked to the assumptions employed to establish a relation between the registered torque and the characteristic stresses and shear rates. In this work, we have paid particular attention to the development of aerated Couette flow configurations to address some of these issues. Not only it is a flexible geometry with a tight and independent control normal and shear stress over a broad range of shear rates, but these units offer a direct way to harmonise the interpretation of data. They provide geometry-independent shear rates and stresses, and the introduction of the new virtual-cell concept removes most of the concerns associated to earlier units. However, their application is still limited, and further work is necessary to assess their viability as an industrial characterisation technique.

Acknowledgements

RO acknowledges financial support from the EPSRC (EP/N034066/1).

References

•  Aït-Kadi  A.,  Marchal  P.,  Choplin  L.,  Chrissemant  A.-S.,  Bousmina  M., Quantitative analysis of mixer-type rheometers using the Couette analogy, The Canadian Journal of Chemical Engineering, 80 (2002) 1166–1174. DOI: 10.1002/cjce.5450800618
•  Andreotti  B.,  Forterre  Y.,  Pouliquen  O., Granular media: between fluid and solid, Cambridge University Press, Cambridge, 2013. ISBN: 9781107034792
•  Anjaneyulu  P.,  Khakhar  D.V., Rheology of a gas-fluidized bed, Powder Technology, 83 (1995) 29–34. DOI: 10.1016/0032-5910(94)02922-b
•  Aranson  I.S.,  Tsimring  L.S., Continuum description of avalanches in granular media, Physical Review E, 64 (2001) 020301. DOI: 10.1103/physreve.64.020301
•  Aranson  I.S.,  Tsimring  L.S., Continuum theory of partially fluidized granular flows, Physical Review E, 65 (2002) 061303. DOI: 10.1103/physreve.65.061303
•  Bagnold  R., Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 225 (1954) 49–63. DOI: 10.1098/rspa.1954.0186
•  Barletta  D.,  Berry  R.J.,  Larsson  S.H.,  Lestander  T.A.,  Poletto  M.,  Ramirez-Gómez  Á., Assessment on bulk solids best practice techniques for flow characterization and storage/handling equipment design for biomass materials of different classes, Fuel Processing Technology, 138 (2015) 540–554. DOI: 10.1016/j.fuproc.2015.06.034
•  Barletta  D.,  Donsì  G.,  Ferrari  G.,  Poletto  M., A rotational tester for the characterization of aerated shear flow of powders, Particle & Particle Systems Characterization, 24 (2007) 259–270. DOI: 10.1002/ppsc.200701115
•  Baumgarten  A.S.,  Kamrin  K., A general fluid-sediment mixture model and constitutive theory validated in many flow regimes, Journal of Fluid Mechanics, 861 (2019) 721–764. DOI: 10.1017/jfm.2018.914
•  Berry  R.J.,  Bradley  M.S.A., Investigation of the effect of test procedure factors on the failure loci and derived failure functions obtained from annular shear cells, Powder Technology, 174 (2007) 60–63. DOI: 10.1016/j.powtec.2006.10.023
•  Berry  R.J.,  Bradley  M.S.A.,  McGregor  R.G., Brookfield powder flow tester. Results of round robin tests with CRM-116 limestone powder, Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 229 (2014) 215–230. DOI: 10.1177/0954408914525387
•  Berzi  D., Extended kinetic theory applied to dense, granular, simple shear flows, Acta Mechanica, 225 (2014) 2191–2198. DOI: 10.1007/s00707-014-1125-1
•  Bishop  A.W.,  Green  G.E.,  Garga  V.K.,  Andresen  A.,  Brown  J.D., A new ring shear apparatus and its application to the measurement of residual strength, Géotechnique, 21 (1971) 273–328. DOI: 10.1680/geot.1971.21.4.273
•  Börzsönyi  T.,  Unger  T.,  Szabó  B.,  Wegner  S.,  Angenstein  F.,  Stannarius  R., Reflection and exclusion of shear zones in inhomogeneous granular materials, Soft Matter, 7 (2011) 8330. DOI: 10.1039/c1sm05762f
•  Bruni  G.,  Barletta  D.,  Poletto  M.,  Lettieri  P., A rheological model for the flowability of aerated fine powders, Chemical Engineering Science, 62 (2007) 397–407. DOI: 10.1016/j.ces.2006.08.060
•  Bruni  G.,  Colafigli  A.,  Lettieri  P.,  Elson  T., Torque measurements in aerated powders using a mechanically stirred fluidized bed rheometer (msFBR), Chemical Engineering Research and Design, 83 (2005) 1311–1318. DOI: 10.1205/cherd.05092
•  Campbell  C.S., Granular shear flows at the elastic limit, Journal of Fluid Mechanics, 465 (2002) 261–291. DOI: 10.1017/s002211200200109x
•  Campbell  C.S., Granular material flows — an overview, Powder Technology, 162 (2006) 208–229. DOI: 10.1016/j.powtec.2005.12.008
•  Capriz  G.,  Giovine  P.,  Mariano  P.M., Mathematical Models of Granular Matter, Springer-Verlag Berlin Heidelberg, Berlin, 2008, ISBN: 9783540782773.
•  Carr  J.F.,  Walker  D.M., An annular shear cell for granular materials, Powder Technology, 1 (1968) 369–373. DOI: 10.1016/0032-5910(68)80019-1
•  Carr  R.L., Evaluating flow properties of solids, Chemical Engineering., 18 (1965) 163–168.
•  Carson  J.W.,  Wilms  H., Development of an international standard for shear testing, Powder Technology, 167 (2006) 1–9. DOI: 10.1016/j.powtec.2006.04.005
•  Castellanos  A.,  Valverde  J.M.,  Quintanilla  M.A.S., The Sevilla Powder Tester: A tool for characterizing the physical properties of fine cohesive powders at very small consolidations, KONA Powder and Particle Journal, 22 (2004) 66–81. DOI: 10.14356/kona.2004011
•  Chen  P.,  Yuan  Z.,  Shen  X.,  Zhang  Y., Flow properties of three fuel powders, Particuology, 10 (2012) 438–443. DOI: 10.1016/j.partic.2011.11.013
•  Chen  W.-K.,  Mizuno  E., Nonlinear Analysis in Soil Mechanics: Theory and Implementation, Elsevier Science Ltd, Amsterdam, New York, NY, U.S.A., 1990.
•  Chen  X.,  Xu  Y.,  Lu  H.,  Guo  X., Effect of the moisture content of straw on the internal friction angle of a granular biomass-coal system, Fuel, 215 (2018) 266–271. DOI: 10.1016/j.fuel.2017.11.013
•  Cheng  X.,  Lechman  J.B.,  Fernandez-Barbero  A.,  Grest  G.S.,  Jaeger  H.M.,  Karczmar  G.S.,  Möbius  M.E.,  Nagel  S.R., Three-Dimensional shear in granular flow, Physical Review Letters, 96 (2006) 038001. DOI: 10.1103/physrevlett.96.038001
•  Chialvo  S.,  Sun  J.,  Sundaresan  S., Bridging the rheology of granular flows in three regimes, Physical Review E, 85 (2012) 021305. DOI: 10.1103/physreve.85.021305
•  Christakis  N.,  Chapelle  P.,  Patel  M.K., Analysis and modeling of heaping behavior of granular mixtures within a computational mechanics framework, Advanced Powder Technology, 17 (2006) 383–398. DOI: 10.1163/156855206777866173
•  Colafigli  A.,  Mazzei  L.,  Lettieri  P.,  Gibilaro  L., Apparent viscosity measurements in a homogeneous gas-fluidized bed, Chemical Engineering Science, 64 (2009) 144–152. DOI: 10.1016/j.ces.2008.08.036
•  Craig  K.,  Buckholz  R.H.,  Domoto  G., An experimental study of the rapid flow of dry cohesionless metal powders, Journal of Applied Mechanics, Transactions ASME, 53 (1986) 935–942. DOI: 10.1115/1.3171884
•  Crawford  N.C.,  Nagle  N.,  Sievers  D.A.,  Stickel  J.J., The effects of physical and chemical preprocessing on the flowability of corn stover, Biomass and Bioenergy, 85 (2016) 126–134. DOI: 10.1016/j.biombioe.2015.12.015
•  da Cruz  F.,  Emam  S.,  Prochnow  M.,  Roux  J.-N.,  Chevoir  F., Rheophysics of dense granular materials: discrete simulation of plane shear flows, Physical Review E, 72 (2005) 021309. DOI: 10.1103/physreve.72.021309
•  Dartevelle  S., Numerical modeling of geophysical granular flows: 1. A comprehensive approach to granular rheologies and geophysical multiphase flows, Geochemistry, Geophysics, Geosystems, 5 (2004) Q08003. DOI: 10.1029/2003gc000636
•  Deshmukh  O.S.,  Dhital  S.,  Mantilla  S.M.O.,  Smyth  H.E.,  Boehm  M.W.,  Baier  S.K.,  Stokes  J.R., Ring shear tester as an in-vitro testing tool to study oral processing of comminuted potato chips, Food Research International, 123 (2019) 208–216. DOI: 10.1016/j.foodres.2019.04.037
•  Dhenge  R.M.,  Washino  K.,  Cartwright  J.J.,  Hounslow  M.J.,  Salman  A.D., Twin screw granulation using conveying screws: Effects of viscosity of granulation liquids and flow of powders, Powder Technology, 238 (2013) 77–90. DOI: 10.1016/j.powtec.2012.05.045
•  Diaz-Bejarano  E.,  Behranvand  E.,  Coletti  F.,  Mozdianfard  M.R.,  Macchietto  S., Organic and inorganic fouling in heat exchangers – Industrial case study: Analysis of fouling state, Applied Energy, 206 (2017) 1250–1266. DOI: 10.1016/j.apenergy.2017.10.018
•  Duffy  S.P.,  Puri  V.M., Evaluation of the computer controlled dynamic yield locus tester, Powder Technology, 101 (1999) 257–265. DOI: 10.1016/s0032-5910(98)00181-8
•  Fan  L.-S.,  Zhu  C., Principles of Gas-Solid Flows, Cambridge University Press, Cambridge, 2005, ISBN: 9780511530142. DOI: 10.1017/CBO9780511530142
•  Feise  H.J.,  Schwedes  J., Investigation of the behaviour of cohesive powder in the biaxial tester, KONA Powder and Particle Journal, 13 (1995) 99–103. DOI: 10.14356/kona.1995014
•  Fitzpatrick  J.J.,  Barry  K.,  Cerqueira  P.S.M.,  Iqbal  T.,  O’Neill  J.,  Roos  Y.H., Effect of composition and storage conditions on the flowability of dairy powders, International Dairy Journal, 17 (2007) 383–392. DOI: 10.1016/j.idairyj.2006.04.010
•  Francia  V.,  Martín  L.,  Bayly  A.E.,  Simmons  M.J.H., The role of wall deposition and re-entrainment in swirl spray dryers, AIChE Journal, 61 (2015) 1804–1821. DOI: 10.1002/aic.14767
•  Freeman  R., Measuring the flow properties of consolidated, conditioned and aerated powders — A comparative study using a powder rheometer and a rotational shear cell, Powder Technology, 174 (2007) 25–33. DOI: 10.1016/j.powtec.2006.10.016
•  Freeman  R.E.,  Cooke  J.R.,  Schneider  L.C.R., Measuring shear properties and normal stresses generated within a rotational shear cell for consolidated and non-consolidated powders, Powder Technology, 190 (2009) 65–69. DOI: 10.1016/j.powtec.2008.04.084
•  García-Triñanes  P.,  Luding  S.,  Shi  H., Tensile strength of cohesive powders, Advanced Powder Technology, 30, 12 (2019) 2868–2880. DOI: 10.1016/j.apt.2019.08.017
•  Garzó  V.,  Dufty  J.W., Dense fluid transport for inelastic hard spheres, Physical Review E, 59 (1999) 5895–5911. DOI: 10.1103/physreve.59.5895
•  Ghadiri  M.,  Ning  Z.,  Kenter  S.J.,  Puik  E., Attrition of granular solids in a shear cell, Chemical Engineering Science, 55–22 (2000) 5445–5456. DOI: 10.1016/S0009-2509(00)00168-8
•  Ghadiri  M.,  Mehrdad  Pasha,  Nan  W.,  Hare  C.,  Vivacqua  V.,  Zafar  U.,  Nezamabadi  S.,  Lopez  A.,  Massih  Pasha,  Nadimi  S., Cohesive powder flow: trends and challenges in characterisation and analysis, KONA Powder and Particle Journal, 37 (2020) 3–18. DOI: 10.14356/kona.2020018
•  Girimonte  R.,  Bernardo  P.,  Minnicelli  A.,  Formisani  B., Experimental characterization of the cohesive behaviour of fine powders by the raining bed test, Powder Technology, 325 (2018) 373–380. DOI: 10.1016/j.powtec.2017.11.038
•  Gnagne  E.H.,  Petit  J.,  Gaiani  C.,  Scher  J.,  Amani  G.N., Characterisation of flow properties of foutou and foufou flours, staple foods in West Africa, using the FT4 powder rheometer, Journal of Food Measurement and Characterization, 11 (2017) 1128–1136. DOI: 10.1007/s11694-017-9489-2
•  Gray  D.D.,  Stiles  J.M., On the constitutive relation for frictional flow of granular materials: Topical report (No. DOE/MC/21353-2584), Morgantown, WV (USA), 1988.
•  Guo  Y.,  Curtis  J.S., Discrete element method simulations for complex granular flows, Annual Review of Fluid Mechanics, 47 (2015) 21–46. DOI: 10.1146/annurev-fluid-010814-014644
•  Guo  Z.,  Chen  X.,  Xu  Y.,  Liu  H., Study of flow characteristics of biomass and biomass-coal blends, Fuel, 141 (2015) 207–213. DOI: 10.1016/j.fuel.2014.10.062
•  Gutam  K.J.,  Mehandia  V.,  Nott  P.R., Rheometry of granular materials in cylindrical Couette cells: Anomalous stress caused by gravity and shear, Physics of Fluids, 25 (2013) 070602. DOI: 10.1063/1.4812800
•  Hammerich  S.,  Stickland  A.D.,  Radel  B.,  Gleiss  M.,  Nirschl  H., Modified shear cell for characterization of the rheological behavior of particulate networks under compression, Particuology, 51 (2020) 1–9. DOI: 10.1016/j.partic.2019.10.005
•  Hanes  D.M.,  Inman  D.L., Observations of rapidly flowing granular-fluid materials, Journal of Fluid Mechanics, 150 (1985) 357–380. DOI: 10.1017/s0022112085000167
•  Hare  C.,  Ghadiri  M., Stress and strain rate analysis of the FT4 Powder Rheometer, EPJ Web of Conferences, 140 (2017) 3034. DOI: 10.1051/epjconf/201714003034
•  Hare  C.,  Ghadiri  M.,  Dennehy  R., Prediction of attrition in agitated particle beds, Chemical Engineering Science, 66 (2011) 4757–4770. DOI: 10.1016/j.ces.2011.06.042
•  Hare  C.,  Zafar  U.,  Ghadiri  M.,  Freeman  T.,  Clayton  J.,  Murtagh  M.J., Analysis of the dynamics of the FT4 powder rheometer, Powder Technology, 285 (2015) 123–127. DOI: 10.1016/j.powtec.2015.04.039
•  Hare  C.,  Zafar  U.,  Ghadiri  M.,  Freeman  T.,  Clayton  J.,  Murtagh  M.J., Correction to “Analysis of the dynamics of the FT4 powder rheometer” [Powder Technol. 285 (2015) 123–127], Powder Technology, 315 (2017) 37–38. DOI: 10.1016/j.powtec.2017.02.061
•  Hartmann  M.,  Palzer  S., Caking of amorphous powders — Material aspects, modelling and applications, Powder Technology, 206-1-2 (2011) 112–121. DOI: 10.1016/j.powtec.2010.04.014
•  Hassanpour  A.,  Ghadiri  M., Characterisation of flowability of loosely compacted cohesive powders by indentation, Particle & Particle Systems Characterization, 24 (2007) 117–123. DOI: 10.1002/ppsc.200601111
•  Hassanpour  A.,  Hare  C.,  Pasha  M., Powder Flow: Theory, Characterisation and Application, RSC Publishing, London, 2019. ISBN: 9781788018470.
•  Hausner  H.H., Friction conditions in a mass of metal powder, International Journal of Powder Metallurgy, 3–14 (1967) 7–13.
•  Hsiau  S.-S.,  Jang  H.-W., Measurements of velocity fluctuations of granular materials in a shear cell, Experimental Thermal and Fluid Science, 17 (1998) 202–209. DOI: 10.1016/s0894-1777(97)10041-3
•  Jaeger  H.M.,  Nagel  S.R.,  Behringer  R.P., Granular solids, liquids, and gases, Reviews of Modern Physics, 68-4 (1996) 1259–1273. DOI: 10.1103/revmodphys.68.1259
•  Jenike  A.W., Storage and Flow of Solids, Rev. ed. Salt Lake City, Utah: University of Utah, 1970.
•  Jenkins  J.T., Dense shearing flows of inelastic disks, Physics of Fluids, 18 (2006) 103307. DOI: 10.1063/1.2364168
•  Johanson  K.,  Barletta  D., The influence of air counter-flow through powder materials as a means of reducing cohesive flow problems, Particle & Particle Systems Characterization, 21 (2004) 316–325. DOI: 10.1002/ppsc.200400939
•  Johnson  P.C.,  Jackson  R., Frictional-collisional constitutive relations for granular materials, with application to plane shearing, Journal of Fluid Mechanics, 176 (1987) 67–93. DOI: 10.1017/s0022112087000570
•  Jop  P.,  Forterre  Y.,  Pouliquen  O., A constitutive law for dense granular flows, Nature, 441 (2006) 727–730. DOI: 10.1038/nature04801
•  Klausner  J.F.,  Chen  D.,  Mei  R., Experimental investigation of cohesive powder rheology, Powder Technology, 112 (2000) 94–101. DOI: 10.1016/S0032-5910(99)00310-1
•  Klein  J.,  Höhne  D.,  Husemann  K., The influence of air permeation on the flow properties of bulk solids, Chemical Engineering & Technology, 26 (2003) 139–146. DOI: 10.1002/ceat.200390020
•  Knight  P.C.,  Seville  J.P.K.,  Wellm  A.B.,  Instone  T., Prediction of impeller torque in high shear powder mixers, Chemical Engineering Science, 56-15 (2001) 4457–4471. DOI: 10.1016/S0009-2509(01)00114-2
•  Koch  D.L., Kinetic theory for a monodisperse gas-solid suspension, Physics of Fluids A: Fluid Dynamics, 2 (1990) 1711–1723. DOI: 10.1063/1.857698
•  Koynov  S.,  Glasser  B.,  Muzzio  F., Comparison of three rotational shear cell testers: Powder flowability and bulk density, Powder Technology, 283 (2015) 103–112. DOI: 10.1016/j.powtec.2015.04.027
•  Krantz  M.,  Zhang  H.,  Zhu  J., Characterization of powder flow: Static and dynamic testing, Powder Technology, 194 (2009) 239–245. DOI: 10.1016/j.powtec.2009.05.001
•  Krishnaraj  K.P.,  Nott  P.R., A dilation-driven vortex flow in sheared granular materials explains a rheometric anomaly, Nature Communications, 7 (2016) 10630. DOI: 10.1038/ncomms10630
•  Ladipo  D.D.,  Puri  V.M., Computer controlled shear cell for measurement of flow properties of particulate materials, Powder Technology, 92 (1997) 135–146. DOI: 10.1016/s0032-5910(97)03230-0
•  Landi  G.,  Barletta  D.,  Lettieri  P.,  Poletto  M., Flow properties of moisturized powders in a Couette fluidized bed rheometer, International Journal of Chemical Reactor Engineering, 10 (2012). DOI: 10.1515/1542-6580.2993
•  Langroudi  M.K.,  Mort  P.R.,  Tardos  G.I., Study of powder flow patterns in a Couette cell with axial flow using tracers and solid fraction measurements, Granular Matter, 13 (2011) 541. DOI: 10.1007/s10035-011-0282-3
•  Langroudi  M.K.,  Turek  S.,  Ouazzi  A.,  Tardos  G.I., An investigation of frictional and collisional powder flows using a unified constitutive equation, Powder Technology, 197 (2010a) 91–101. DOI: 10.1016/j.powtec.2009.09.001
•  Langroudi  M.K.,  Turek  S.,  Ouazzi  A.,  Tardos  G.I., Corrigendum to “An investigation of frictional and collisional powder flows using a unified constitutive equation” [Powder Technology (197) 91–101], Powder Technology, 198 (2010b) 314. DOI: 10.1016/j.powtec.2009.11.020
•  Léonard  G.,  Abatzoglou  N., Stress distribution in lubricated vs unlubricated pharmaceutical powder columns and their container walls during translational and torsional shear testing, Powder Technology, 203 (2010) 534–547. DOI: 10.1016/j.powtec.2010.06.020
•  Leung  L.Y.,  Mao  C.,  Srivastava  I.,  Du  P.,  Yang  C.-Y., Flow function of pharmaceutical powders is predominantly governed by cohesion, not by friction coefficients, Journal of Pharmaceutical Sciences, 106 (2017) 1865–1873. DOI: 10.1016/j.xphs.2017.04.012
•  Louati  H., Experimental and numerical study of humid granular material: influence of liquid content in quasi-static regime, Ecole des Mines d’Albi-Carmaux, 2016.
•  Louati  H.,  Oulahna  D.,  de Ryck  A., Apparent friction and cohesion of a partially wet granular material in steady-state shear, Powder Technology, 278 (2015) 65–71. DOI: 10.1016/j.powtec.2015.03.011
•  Louati  H.,  Oulahna  D.,  de Ryck  A., Effect of the particle size and the liquid content on the shear behaviour of wet granular material, Powder Technology, 315 (2017) 398–409. DOI: 10.1016/j.powtec.2017.04.030
•  Ludwig  B.,  Millington-Smith  D.,  Dattani  R.,  Adair  J.H.,  Posatko  E.P.,  Mawby  L.M.,  Ward  S.K.,  Sills  C.A., Evaluation of the hydrodynamic behavior of powders of varying cohesivity in a fluidized bed using the FT4 Powder Rheometer®, Powder Technology, 371 (2020) 106–114. DOI: 10.1016/j.powtec.2020.05.042
•  Lun  C.K.K.,  Savage  S.B.,  Jeffrey  D.J.,  Chepurniy  N., Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield, Journal of Fluid Mechanics, 140 (1984) 223–256. DOI: 10.1017/s0022112084000586
•  Lupo  M.,  Schütz  D.,  Riedl  E.,  Barletta  D.,  Poletto  M., Assessment of a powder rheometer equipped with a cylindrical impeller for the measurement of powder flow properties at low consolidation, Powder Technology, 357 (2019) 281–290. DOI: 10.1016/j.powtec.2019.08.071
•  Marchal  P.,  Smirani  N.,  Choplin  L., Rheology of dense-phase vibrated powders and molecular analogies, Journal of Rheology, 53 (2009) 1–29. DOI: 10.1122/1.3037266
•  Mehandia  V.,  Gutam  K.J.,  Nott  P.R., Anomalous stress profile in a sheared granular column, Physical Review Letters, 109 (2012) 128002. DOI: 10.1103/PhysRevLett.109.128002
•  Midi  G.D.R., On dense granular flows, European Physical Journal E, 14 (2004) 341–365. DOI: 10.1140/epje/i2003-10153-0
•  Mort  P.R., Scale-up and control of binder agglomeration processes - Flow and stress fields, Powder Technology, 189 (2009) 313–317. DOI: 10.1016/j.powtec.2008.04.022
•  Moucheront  P.,  Bertrand  F.,  Koval  G.,  Tocquer  L.,  Rodts  S.,  Roux  J.-N.,  Corfdir  A.,  Chevoir  F., MRI investigation of granular interface rheology using a new cylinder shear apparatus, Magnetic Resonance Imaging, 28 (2010) 910–918. DOI: 10.1016/j.mri.2010.01.007
•  Mueth  D.M.,  Debregeas  G.F.,  Karczmar  G.S.,  Eng  P.J.,  Nagel  S.R.,  Jaeger  H.M., Signatures of granular microstructure in dense shear flows, Nature, 406 (2000) 385–389. DOI: 10.1038/35019032
•  Nan  W.,  Ghadiri  M.,  Wang  Y., Analysis of powder rheometry of FT4: Effect of particle shape, Chemical Engineering Science, 173 (2017a) 374–383. DOI: 10.1016/j.ces.2017.08.004
•  Nan  W.,  Ghadiri  M.,  Wang  Y., Analysis of powder rheometry of FT4: Effect of air flow, Chemical Engineering Science, 162 (2017b) 141–151. DOI: 10.1016/j.ces.2017.01.002
•  Ogata  K., A review: Recent progress on evaluation of flowability and floodability of powder, KONA Powder and Particle Journal, 36 (2019) 33–49. DOI: 10.14356/kona.2019002
•  Ono  T.,  Yonemochi  E., Evaluation of the physical properties of dry surface-modified ibuprofen using a powder rheometer FT4 and analysis of the influence of pharmaceutical additives on improvement of the powder flowability, International Journal of Pharmaceutics, 579 (2020) 119165. DOI: 10.1016/j.ijpharm.2020.119165
•  Opaliński  I.,  Chutkowski  M.,  Stasiak  M., Characterizing moist food-powder flowability using a Jenike shear-tester, Journal of Food Engineering, 108 (2012) 51–58. DOI: 10.1016/j.jfoodeng.2011.07.031
•  Orband  J.L.R.,  Geldart  D., Direct measurement of powder cohesion using a torsional device, Powder Technology, 92 (1997) 25–33. DOI: 10.1016/s0032-5910(97)03212-9
•  Orlando  A.D.,  Shen  H.H., Effect of particle size and boundary conditions on the shear stress in an annular shear cell, Granular Matter, 14 (2012) 423–431. DOI: 10.1007/s10035-012-0313-8
•  Pastor  M.,  Blanc  T.,  Pastor  M.J., A depth-integrated viscoplastic model for dilatant saturated cohesive-frictional fluidized mixtures: Application to fast catastrophic landslides, Journal of Non-Newtonian Fluid Mechanics, 148 (2009) 142–153. DOI: 10.1016/j.jnnfm.2008.07.014
•  Petford  N., Rheology of granitic magmas during ascent and emplacement, Annual Review of Earth and Planetary Sciences, 31 (2003) 399–427. DOI: 10.1146/annurev.earth.31.100901.141352
•  Pouliquen  O., Scaling laws in granular flows down rough inclined planes, Physics of Fluids, 11 (1999) 542–548. DOI: 10.1063/1.869928
•  Rao  K.K.,  Nott  P.R., An Introduction to Granular Flow, Cambridge University Press, ISBN: 9780511611513, 2008. DOI: 10.1017/CBO9780511611513
•  Sakaie  K.,  Fenistein  D.,  Carroll  T.J.,  van Hecke  M.,  Umbanhowar  P., MR imaging of Reynolds dilatancy in the bulk of smooth granular flows, EPL (Europhysics Letters), 84 (2008) 38001. DOI: 10.1209/0295-5075/84/38001
•  Salehi  H.,  Barletta  D.,  Poletto  M., A comparison between powder flow property testers, Particuology, 32 (2017a) 10–20. DOI: 10.1016/j.partic.2016.08.003
•  Salehi  H.,  Barletta  D.,  Poletto  M.,  Schütz  D.,  Romirer  R., On the use of a powder rheometer to characterize the powder flowability at low consolidation with torque resistances, AIChE Journal, 63 (2017b) 4788–4798. DOI: 10.1002/aic.15934
•  Salehi  H.,  Sofia  D.,  Schütz  D.,  Barletta  D.,  Poletto  M., Experiments and simulation of torque in Anton Paar powder cell, Particulate Science and Technology, 36 (2018) 501–512. DOI: 10.1080/02726351.2017.1409850
•  Savage  S.B., Analyses of slow high-concentration flows of granular materials, Journal of Fluid Mechanics, 377 (1998) 1–26. DOI: 10.1017/s0022112098002936
•  Savage  S.B.,  Sayed  M., Stresses developed by dry cohesionless granular materials sheared in an annular shear cell, Journal of Fluid Mechanics, 142 (1984) 391–430. DOI: 10.1017/S0022112084001166
•  Schulze  D., Development and application of a novel ring shear tester, Aufbereitungstechnik, 35 (1994) 524–535.
•  Schulze  D., Practical determination of flow properties, in: Powders and Bulk Solids: Behavior, Characterization, Storage and Flow, Springer Berlin Heidelberg, 2008, pp. 163–198. DOI: 10.1007/978-3-540-73768-1_6
•  Schwedes  J., Measurement of flow properties of bulk solids, Powder Technology, 88 (1996) 285–290. DOI: 10.1016/s0032-5910(96)03132-4
•  Schwedes  J., Review on testers for measuring flow properties of bulk solids, Granular Matter, 5 (2003) 1–43. DOI: 10.1007/s10035-002-0124-4
•  Shimada  Y.,  Hatano  S.,  Matsusaka  S., A new method for evaluating powder flowability using constant-volume shear tester, Advanced Powder Technology, 29 (2018a) 3577–3583. DOI: 10.1016/j.apt.2018.08.028
•  Shimada  Y.,  Kawata  T.,  Matsusaka  S., Analysis of constant-volume shear tests based on precise measurement of stresses in powder beds, Advanced Powder Technology, 29 (2018b) 1372–1378. DOI: 10.1016/j.apt.2018.02.033
•  Srivastava  A.,  Sundaresan  S., Analysis of a frictional-kinetic model for gas-particle flow, Powder Technology, 129 (2003) 72–85. DOI: 10.1016/s0032-5910(02)00132-8
•  Sun  J.,  Sundaresan  S., A constitutive model with microstructure evolution for flow of rate-independent granular materials, Journal of Fluid Mechanics, 682 (2011) 590–616. DOI: 10.1017/jfm.2011.251
•  Sundaresan  S., Some outstanding questions in handling of cohesionless particles, Powder Technology, 115 (2001) 2–7. DOI: 10.1016/S0032-5910(00)00423-X
•  Swize  T.,  Osei-Yeboah  F.,  Peterson  M.L.,  Boulas  P., Impact of shear history on powder flow characterization using a~ring shear tester, Journal of Pharmaceutical Sciences, 108 (2019) 750–754. DOI: 10.1016/j.xphs.2018.07.003
•  Tang  Z.,  Brzinski  T.A.,  Shearer  M.,  Daniels  K.E., Nonlocal rheology of dense granular flow in annular shear experiments, Soft Matter, 14 (2018) 3040–3048. DOI: 10.1039/c8sm00047f
•  Tardos  G.I.,  Khan  M.I.,  Schaeffer  D.G., Forces on a slowly rotating, rough cylinder in a Couette device containing a dry, frictional powder, Physics of Fluids, 10 (1998) 335–341. DOI: 10.1063/1.869525
•  Tardos  G.I.,  McNamara  S.,  Talu  I., Slow and intermediate flow of a frictional bulk powder in the Couette geometry, Powder Technology, 131 (2003) 23–39. DOI: 10.1016/s0032-5910(02)00315-7
•  Taylor  M.K.,  Ginsburg  J.,  Hickey  A.J.,  Gheyas  F., Composite method to quantify powder flow as a screening method in early tablet or capsule formulation development, AAPS PharmSciTech, 1 (2000) 20–30. DOI: 10.1208/pt010318
•  Teunou  E.,  Fitzpatrick  J.J., Effect of relative humidity and temperature on food powder flowability, Journal of Food Engineering, 42 (1999) 109–116. DOI: 10.1016/s0260-8774(99)00087-4
•  Teunou  E.,  Fitzpatrick  J.J., Effect of storage time and consolidation on food powder flowability, Journal of Food Engineering, 43 (2000) 97–101. DOI: 10.1016/s0260-8774(99)00137-5
•  Teunou  E.,  Fitzpatrick  J.J.,  Synnott  E.C., Characterisation of food powder flowability, Journal of Food Engineering, 39 (1999) 31–37. DOI: 10.1016/s0260-8774(98)00140-x
•  Thakur  S.C.,  Ahmadian  H.,  Sun  J.,  Ooi  J.Y., An experimental and numerical study of packing, compression, and caking behaviour of detergent powders, Particuology, 12 (2014) 2–12. DOI: 10.1016/j.partic.2013.06.009
•  Tomasetta  I.,  Barletta  D.,  Lettieri  P.,  Poletto  M., The measurement of powder flow properties with a mechanically stirred aerated bed, Chemical Engineering Science, 69 (2012) 373–381. DOI: 10.1016/j.ces.2011.10.056
•  Tsao  H.-K.,  Koch  D.L., Simple shear flows of dilute gas-solid suspensions, Journal of Fluid Mechanics, 296 (1995) 211–245. DOI: 10.1017/s0022112095002114
•  Tsunakawa  H.,  Aoki  R., Measurements of the failure properties of granular materials and cohesive powders, Powder Technology, 33 (1982) 249–256. DOI: 10.1016/0032-5910(82)85063-8
•  Vescovi  D.,  Berzi  D.,  Richard  P.,  Brodu  N., Plane shear flows of frictionless spheres: Kinetic theory and 3D soft-sphere discrete element method simulations, Physics of Fluids, 26 (2014) 53305. DOI: 10.1063/1.4879267
•  Vidyapati  V.,  Kheiripour Langroudi  M.,  Sun  J.,  Sundaresan  S.,  Tardos  G.I.,  Subramaniam  S., Experimental and computational studies of dense granular flow: Transition from quasi-static to intermediate regime in a Couette shear device, Powder Technology, 220 (2012) 7–14. DOI: 10.1016/j.powtec.2011.09.032
•  Viswanath  D.S.,  Ghosh  T.,  Prasad  D.H.L.,  Dutt  N.V.K.,  Ran  K.Y., Viscosity of liquids: Theory, estimation, experiment, and data, Springer Netherlands, Amsterdan, 2007. ISBN: 9781402054822
•  Vun  S.,  Naser  J.,  Witt  P., Extension of the kinetic theory of granular flow to include dense quasi-static stresses, Powder Technology, 204 (2010) 11–20. DOI: 10.1016/j.powtec.2010.07.001
•  Wang  Y.,  Koynov  S.,  Glasser  B.J.,  Muzzio  F.J., A method to analyze shear cell data of powders measured under different initial consolidation stresses, Powder Technology, 294 (2016) 105–112. DOI: 10.1016/j.powtec.2016.02.027
•  Wheeler  S.J.,  Sivakumar  V., An elasto-plastic critical state framework for unsaturated soil, Geotechnique, 45 (1995) 35–53. DOI: 10.1680/geot.1995.45.1.35
•  Wildman  R.D.,  Martin  T.W.,  Huntley  J.M.,  Jenkins  J.T.,  Viswanathan  H.,  Fen  X.,  Parker  D.J., Experimental investigation and kinetic-theory-based model of a rapid granular shear flow, Journal of Fluid Mechanics, 602 (2008) 63–79. DOI: 10.1017/s0022112008000700
•  Wu  C.Y.,  Hung  W.L.,  Miguélez-Morán  A.M.,  Gururajan  B.,  Seville  J.P.K., Roller compaction of moist pharmaceutical powders, International Journal of Pharmaceutics, 391 (2010) 90–97. DOI: 10.1016/j.ijpharm.2010.02.022
•  Wu  K., Francia  V.,  Coppens  M.O., Dynamic viscoplastic granular flows: A persistent challenge in gas-solid fluidization, Powder Technology, 365 (2020) 172–185. DOI: 10.1016/j.powtec.2019.04.053
•  Yahia  L.A.A.,  Piepke  T.M.,  Barrett  R.,  Ozel  A.,  Ocone  R., Development of a virtual Couette rheometer for aerated granular material, AIChE Journal, 66 (2020) e16945. DOI: 10.1002/aic.16945
•  Yang  L.,  Padding  J.T.,  Kuipers  J.A.M, Modification of kinetic theory of granular flow for frictional spheres, Part I: Two-fluid model derivation and numerical implementation, Chemical Engineering Science, 152 (2016) 767–782. DOI: 10.1016/j.ces.2016.05.031
•  Zafar  U.,  Hare  C.,  Calvert  G.,  Ghadiri  M.,  Girimonte  R.,  Formisani  B.,  Quintanilla  M.A.S.,  Valverde  J.M., Comparison of cohesive powder flowability measured by Schulze shear cell, Raining bed method, Sevilla Powder Tester and new Ball Indentation Method, Powder Technology, 286 (2015) 807–816. DOI: 10.1016/j.powtec.2015.09.010
•  Zulfiqar  M.,  Moghtaderi  B.,  Wall  T.F., Flow properties of biomass and coal blends, Fuel Processing Technology, 87 (2006) 281–288. DOI: 10.1016/j.fuproc.2004.10.007

Authors’ Short Biographies

Victor Francia

Victor Francia is an Assistant Professor of Mechanical Engineering at Heriot-Watt University, Edinburgh, UK, with industrial and consulting experience in the water, energy and consumer good sectors. He moved to academia in 2012, working at Imperial College London and later at University College London before starting in his research group in 2019 on multi-phase flow and responsive technology. He looks into complex particle flows, how we can control dynamic structures using external actuation to design smart technology and new devices able to self-regulate and improve efficiency in the process industry and the environmental and energy sectors.

Lyes Ait Ali Yahia

Dr. Lyes Ait Ali Yahia is a Research Associate in the Institute of Mechanical, Process and Energy Engineering at Heriot-Watt University, Edinburgh. He was awarded a Ph.D. in Science Engineering and Environment at the University of Paris EST Creteil, France. After his doctoral studies on aerosol physics, he worked as a Teacher/Researcher Fellow in the University of Paris EST Creteil. Since then, he has been working at Heriot-Watt University on the rheology of granular materials where the focus of his work is to design experimental procedures that will help understand the flow behaviour of granular materials.

Raffaella Ocone

Raffaella Ocone OBE FREng FRSE holds the Chair of Chemical Engineering in the School of Engineering and Physical Sciences at Heriot-Watt University (UK) since 1999. She has worked at the Università di Napoli (Italy); Claude Bérnard Université, Lyon (France); Louisiana State University (USA); Princeton University (USA). In 2017 she became the first “Caroline Herschel Visiting Professor” in Engineering at RUHR Universität (Germany); in 2018 she was awarded a Visiting Research Fellowship from the Institute for Advanced Studies at Università di Bologna (Italy). Raffaella’s main interests include the modelling of complex reactive systems and the hydrodynamics of granular media.

Ali Ozel

Dr Ali Ozel is an Assistant Professor in the Institute of Mechanical, Process and Energy Engineering at Heriot-Watt University, Edinburgh. He was awarded a Ph.D. in Fluid Mechanics at the National Polytechnic Institute of Toulouse, France. After his doctoral studies, he worked as a post-doctoral fellow at the Fluid Mechanics Institute of Toulouse. Before joining Heriot-Watt University, he was as an associate research scholar in the Department of Chemical and Biological Engineering at Princeton University. He has been working on the development and deployment of state-of-the-art mathematical and computational modelling and simulation tools to study particle-laden flows and complex fluids.