A Review of Advanced Ball Mill Modelling

Abstract

In the early 1990s the discrete element method (DEM) was used for the first time to simulate media motion in tumbling mills. Although it has been over a quarter of a century since this tool was first used to predict media motion it has not yet reached maturity to be used in predicting product size distribution and throughput of tumbling mills. However, there has not been shortage of attempts to do so. The literature is relatively vast in the topic and researchers who embark in this area of research will find it difficult to understand the current status of development and also the similarities and fundamental differences that exist amongst the various approaches that have been proposed and pursued over the years. The paper reviews the literature on the application of models based on distributed collision energy information to predict size reduction in tumbling mills, in particular ball mills, analyzing critically various approaches proposed, their limitations and achievements, identifying areas that still require development until the technology becomes ready for being used for optimizing and designing ball mills. Finally, the advances recently accomplished on the approach proposed by the author and his co-workers are then reviewed in greater detail.

1. Introduction

In spite of the development and increase in popularity of several other technologies, such as vertical roller mills, stirred media mills and high-pressure grinding rolls, ball mills still retain a significant part of their importance in grinding, being widely used from minerals and cement, to chemicals and ceramics. The operation of a ball mill is a capital- and energy-intensive process, so that even marginal improvements in their efficiency result in immense benefits to the industry. These mills are more often of the tumbling type, but also include planetary and vibratory mills, which have all in common the analogous type of motion of the loose grinding media. It has been long recognized that in order to reduce their size, materials require the application of energy in some form. This recognition led to attempts to relate energy and size reduction from the latter part of the 19th century (von Rittinger, 1867; Kick, 1885) throughout the 20th century (Bond, 1952; Charles, 1957), and even more recently (Morrell, 2004).

These different approaches have one thing in common: they use a single number to describe energy in grinding. This number, the specific energy, is the ratio between the power and the throughput in the case of continuous systems, or the power multiplied by the grinding time per unit mass of powder or ore in batch mills. Given typically in kWh/t, it has long been recognized as the most important descriptor of the contribution of the process to the outcome of comminution. The importance of specific energy and the knowledge on how mill power can be controlled by varying mill design and operating variables, has allowed engineers design mills and improve a large number of operations throughout the 20th century (Herbst and Fuerstenau, 1980). These so-called energy-size reduction relationships were originally only used as one-size descriptors of comminution (Bond, 1952), but with the advent of the size-mass balance, or population balance model (Herbst and Fuerstenau, 1980), improvements from this type of relationships also became useful to describe the change of the entire size distribution from the feed to the product.

A more in-depth look at ball mill operation clearly suggests the richness of the information hidden behind the value of specific energy in an operation, which should be regarded as merely an average number. The emphasis on this number suggests, in principle, that it would not matter how the material receives energy, just the amount. Single-particle breakage has allowed us to gain insights into this by analyzing the different outcomes if a particle receives energy in the form of a single high-energy impact from the grinding media, or from a multitude of very low-energy impacts, which have very different outcomes (Pauw and Maré, 1988; Tavares, 2004). Evidence of this also appears in the form of the empirical equations that have been used to account for several variables in grinding in tumbling mills that are part of the design method of Bond (Rowland and Kjos, 1980), as well as to the need for the user to conduct additional batch grinding tests to fit some of the model parameters in the case of the scale-up method proposed by Herbst and Fuerstenau (1980).

As such, great value can be gained by using distributed information on specific comminution energies, rather than averages. Such information has already been available from careful experimentation or, more commonly, simulations using the discrete element method (DEM), which conveniently allows predicting the distribution of collision energies in a mill (Weerasekara et al., 2013), creating an alternative to the lumped specific energy information used to date to describe size reduction in mills. DEM makes it possible to predict how collisions vary in magnitude and frequency as the geometry, the ball charge and the mill speed are varied. Therefore, instead of correlating each individual parameter such as mill diameter, filling, speed and ball size, for instance, to the product size, one can directly take into account the record of the collisions and their influence on the particle size distribution in the mill.

There has been no shortage in the last 25 years or so of approaches to use such distributed collision energy information in modelling ball mills. However, it is not straightforward to identify how they differ, their benefits and challenges in their goal of replacing the traditional energy-size reduction methods such as Bond’s (Bond, 1952) or population balance model (PBM) formulations (Herbst and Fuerstenau, 1980; Austin et al., 1984). The present work focuses primarily on the research dedicated to predict particle breakage in ball mills, analyzing in particular DEM-based approaches to predict size reduction in mills, called here “advanced models”. As such, this review does not directly cover other aspects that are also necessary to predict grinding in continuous systems, such as material transport and internal classification, which also were the object of much research throughout the last quarter of century.

2. Advanced mill modelling prior to DEM

The first attempts in coupling impact energy information to particle breakage data to predict grinding have been made in the late 1980s and early 1990s. These were used to predict the functions that make up the traditional population balance model. The greatest difficulty at the time was associated to the collection of information on the collision energies in the mill. Yashima et al. (1988) and Nomura et al. (1991) estimated the size-dependent rates of breakage of particles contained in ball mills using single-particle slow compression data and experimental measurements of impact energy spectra using load sensors positioned in the shell of a lab mill, showing some qualitative agreement. Cho (1987) and Höfler and Herbst (1990) demonstrated how both the breakage rate and the breakage distribution functions varied with collision energy, using data from particle bed breakage tests and impact energy spectra from tests in a batch mill. Their work proposed that the breakage function B_ij commonly used in the traditional population balance model could be interpreted as the weighed-average of the energy-dependent breakage distribution function values B_ij(E_m,k), giving (Cho, 1987)   

$$B_{ij}=\sum _{k=1}^{n}p\left(E_{\text{m},k}\right)B_{ij}(E_{\text{m},k})$$(1)

where p(E_m,k) is the fraction of collisions with specific energy level E_m,k. This equation could be used, associated to the breakage rate or selection function (S_i) to predict grinding in a batch mill using the equation (Austin et al., 1984)   

$$\frac{\text{d}{w}_i}{\text{d}t}=-S_i{w}_i+\sum _{j=1}^{i-1}{S}_j{b}_{ij}{w}_j$$(2)

where w_i is the fraction of particles in size class i at time t and b_ij is the breakage function in density form, so that b_ij = B_ij – B_i–1,j.

This is certainly a more logical and intuitive approach than assuming a constant breakage distribution function, as used in the traditional PBM formulation of ball milling. These approaches, however, had the serious limitation of requiring impact energy data, which was very difficult to estimate experimentally. In the case of Cho (1987), the distribution of collision energies was back-calculated from batch grinding data, so that it should be understood as only a proof of concept of the modeling approach.

3. Role of DEM in advanced mill modelling

A major advance in the modeling of ball mills became possible through the development of the discrete element method. DEM provides a numerical procedure for solving Newton’s second law with an appropriate contact relationship that can be applied to describe the motion of each grinding medium contained in the mill charge to predict element position, velocity and forces of interaction over time. Very good reviews of the method when applied to comminution can be found elsewhere (Cleary, 1998; Weerasekara et al., 2013). The relevance of the method when applied to milling lies in its ability to account for the effects of a number of variables explicitly, including mill speed, mill filling, ball size distribution and liner configuration. It was first applied to simulate ball milling by Mishra and Rajamani (1992), who originally described media motion in two dimensions. The technique is now packaged in a number of commercial as well as open source software, being able to describe media motion in three dimensions, which is critical to provide the quantitative information required for mill simulation (Powell and McBride, 2006; Morrison and Cleary, 2008).

In DEM, particles are either considered undeformable (hard) or deformable (soft) (O’Sullivan, 2011). The latter, in which particles are allowed to overlap, is the most commonly used. It is supported by proper constitutive laws describing the contacts, with Hertz-Mindlin being the most commonly used (Weerasekara et al., 2013).

Algorithms that allow describing particle breakage inside the DEM environment are more recent developments, and include the discrete grain breakage (Herbst and Potapov, 2004), the bonded particle model (Potyondy and Cundal, 2004) and the particle replacement (Cleary, 2001). As such, DEM with the proper description of particle breakage appeared as a complete and empiricism-free solution to the current approaches used in modeling ball mills, since it does not only allow describing media motion, but also breakage of particles inside the charge (Morrison and Cleary, 2008). Indeed, as a proof of concept, some researchers have demonstrated that it is possible to include particles in mill simulations and follow them as they tumble and are progressively broken by the balls. Indeed, Herbst and Potapov (2004) included polyhedral particles that broke inside the charge, Metzger and Glasser (2013) described breakage of particles inside a batch mill using the bonded particle model, while Delaney et al. (2013) described breakage of particles in a pilot mill using the particle replacement method. Unfortunately, this intuitive approach is not yet feasible to be used in any realistic way to simulate industrial ball mills, since breakage algorithms add to the already high computational demand for simulating these mills and also can lead to an “explosion” on the number of particles in the simulations, making computation unfeasible at this time. However, such techniques are quickly reaching maturity for application in simulation of a number of crusher types (Cleary and Sinnott, 2015; Quist and Evertsson, 2016; Barrios and Tavares, 2016). With increasing computation power, these techniques will become, however, gradually more applicable to tumbling mills, in particular of the autogenous and semi-autogenous type, given that the autogenous media not only also transfers energy but also undergoes breakage.

DEM simulation of industrial tumbling mills can represent a challenge even in the absence of breakage in the DEM environment. This is because the powder or ore particles are much finer in size than the grinding media, leading to difficulty in keeping track of the immense number of particles contained in full-scale mills, besides the need to reduce the time step to avoid overlapping the media with the smallest powder particles (Cleary and Morrison, 2011). The first limitation can be illustrated with a simple example: the most common tumbling mill used in the lab is the Bond ball mill, used to measure the widely used Bond ball mill work index (Bond, 1952). The mill dimensions, 30 cm in diameter and 30 cm in length, and the test conditions are standardized, with a maximum ball size of 40 mm and an ore top size of 3.35 mm. With less than 300 balls, it poses no challenge in running the simulations, if only grinding media are included (Fig. 1). For such a small mill and operating at both low mill filling (20 %) and powder filling (50 %), one could include also the powder charge. Indeed, for a typical powder size distribution, it would be possible to include particles as fine as about 0.5 mm before running out of memory using today’s desktop computers, since it could take as much as 10 GB of computer memory to run them, for instance, in a commercial software such as EDEM^® (DEM Solutions, UK) which is substantial (Fig. 1). However, if the case of a large-diameter industrial mill is considered, which could have, for instance, 8 m of internal diameter, the user would already run out of memory if he included particles with the top size in the feed, if the same ball and particle size distributions simulated in the laboratory mill are used. Moreover, this is only considering a 30 cm slice of the mill, which could have more than two billion elements with sizes above 0.5 mm (Fig. 1).

Fig. 1

Number of particles used in simulating 30 cm slices of mills with different diameters (balls in size range of 40–15 mm) and powder following the cumulative size distribution given by Passing = (x/3.35)^0.5, where particle size x is given in mm (20 % ball filling, 50 % interstitial powder filling). Powder finer than designated size is accumulated in the informed size.

Nevertheless, it is worth mentioning that the increase in computing power in recent years has enticed researchers to include both grinding media and powder in some simulations of small ball mills, which has been particularly useful to understand the collision frequencies and energies involved in media-particle contacts (Cleary and Morrison, 2011; Wang et al., 2012; Capece et al., 2014). This type of simulations, however, represents a challenge in gathering collision information, since the event of a particle being nipped by two colliding media is logged as two separate collisions of lower magnitude.

One pragmatic solution to this in the case of ball mills is to simplify the problem by not including the ore or powder particles in DEM, only the grinding media in the simulations, calculating the product size distribution and the mill capacity in a post-processing stage using a PBM scheme on the basis of the frequencies and magnitudes of collisions, that, is, the collision energy spectrum, experienced by particles in the mill. The key advantage of this approach is that the milling environment can be decoupled from the ore or powder in size reduction, while the main challenge is related to the fact that the mass of material and sizes of particles involved in each of the collisions are not known. Also, this approach is only valid whenever the contribution of the ore or powder particles in transferring energy and inducing breakage in other particles is negligible, which is a valid assumption in the case of ball mills. As such, DEM would be given the role of only providing information on the mechanical environment in the mill, since the ore particles would not appear explicitly in the simulations. Powell et al. (2008) called these ore particles “sub-DEM particles”, since they would be the background material that is subjected to the collisions through being entrapped between the colliding media, but would not appear in the DEM simulations explicitly.

In order to ensure that predictions of the collision energy spectra under these circumstances are realistic, it is important to ensure that DEM simulations can predict mill media motion accurately. This problem is not straightforward since the absence of powder (ore) in the DEM simulations would need to be compensated by modifying some—if not all—of the contact parameters that govern the contacts between balls and between them and the mill liners. This can only be accomplished by proper contact parameter estimation, which is reviewed elsewhere (Mishra and Murty, 2001). As such, the user should be aware that apparent contact parameters and not standard parameters for steel-steel contacts (whenever steel media are used), for instance, should be used in these simulations, given the dissipative effect of the background powder. Typically, the presence of powder increases the rolling and sliding friction of the ball charge, while it reduces the coefficient of restitution in the Hertz-Mindlin model. Obvious challenges are associated to the variation of the motion of the charge as particles become finer. This evidently further complicates matters when using data from batch milling to calibrate DEM contact parameters, which is common.

It is common to select contact parameters in DEM simulations so as to match the power predicted to the one measured either in a batch or an industrial mill. However, caution should be exercised in not using it as the only target when selecting values of contact parameters in ball mill simulations. It is known that several sets of plausible contact parameters can approximately match the measured mill power, but with reasonably distinct patterns of media motion (Martins et al., 2012; Chagas et al., 2015). Positions of toe and shoulder of the charge, monitored by video recordings of batch mills fitted with a transparent end covers (Moys et al., 2000; Venugopal and Rajamani, 2001), the position and velocity of an instrumented ball (Martins et al., 2012) or of an irradiated ball using positron emission particle tracking (PEPT) (Govender et al., 2013; Chagas et al., 2015), are excellent alternatives to be used in conjunction with net mill power to calibrate contact parameters for effective mill simulations.

Once the mill geometry, velocity and the charge size distribution have been defined, and the various material and contact parameters selected, the mill can then be simulated. It is important to ensure, though, that a steady motion of the media has been established, which takes several revolutions if the charge is initially in repose. After this is established, the mill can then be simulated for a sufficient period of time to give a consistent output, which is about two revolutions (Powell et al., 2008), during which detailed information on the collisions are recorded. At this point the simulation is interrupted and the interactions between grinding media and between them and the mill liners are binned for analysis at a post-processing stage. This analysis provides the probability distributions, which in effect are the rates at which grinding media interact. The question then arises about the collision energy information that will be harnessed from DEM. Three options have been considered by researchers:

• • the dissipated energy
• • the maximum impact energy
• • the kinetic energy

The dissipated energy, also called energy loss, results from the inelastic contact between grinding media or grinding media and an ore particle, that mimics dissipative processes such as plastic deformation or breakage. It is calculated as the integral of the damping forces with respect to the displacements over a whole contact period, accounting for the contributions of both the normal (n) and the shear (s) components of the contact:   

$$E=E_{\text{n}}+E_{\text{s}}={\int }_0^{t_{\text{contact}}}{F}_{\text{n}}\text{d}{\xi }_{\text{n}}+{\int }_0^{t_{\text{contact}}}{F}_{\text{s}}\text{d}{\xi }_{\text{s}}$$(3)

where F_n and F_s are the components of the contact force in the normal and shear directions, respectively, and t_contact is the total contact time during a collision.

The maximum impact energy, characterizing the maximum stress experienced in the collision, is the integral of the contact force and displacement in the normal direction when the overlap between two particles reaches the maximum (Wang et al., 2012).

The kinetic energy in the collision between two grinding media is calculated by $1/2m_{\text{b}}{v}_{ij}^2$, where ν_ij (= ν_i – ν_j) is the relative normal velocity of the two grinding media at the collision and m_b is average ball mass (= (m_b,i + m_b,j)/2) for media–media collision or the mass of one ball for ball-liner collision, whereas the reduced mass, given by (= 2m_b,im_b,j/(m_b,i + m_b,j)) is also often used (Kwan et al., 2005).

It is convenient, for comparison purposes, to represent distributions of collision energies in the form of cumulative distribution functions P(E) and total frequency of collisions ω. Cumulative distributions are illustrated in Fig. 2 for different liner configurations in a batch mill. Whenever necessary the distribution of collision energies in density form in the mill p(E) may be calculated from the cumulative distribution, with p(E) = dP(E)/dE.

Fig. 2

Collision energy distributions for a 0.6 m diameter mill with different liner profiles balls at 67 % of critical speed, 30 % mill filling and 25 mm steel balls.

Finally, when grinding is carried out wet, the presence of water would also influence the contact parameters. As such, coupling of DEM and techniques such as computational fluid dynamics (CFD) or smoothed particle hydrodynamics (SPH) would allow realistic description of the influence of the fluid medium (Cleary et al., 2006). The fidelity of the simulation models able to predict breakage will then determine whether or not it is feasible to still use predictions from ball-only DEM simulations or coupled DEM-CFD or DEM-SPH simulations to predict media motion. In this case it is important to acknowledge the effect of the presence of water on dampening the collisions (Mayank et al., 2015).

4. DEM-based models of mills

4.1 Models that use lumped information from DEM

Resorting to empiricism, some researchers have attempted to couple either the total or an average collision energy or power obtained using DEM to breakage rates or other measures of breakage intensity from batch grinding experiments (Kano and Saito, 1998; Mori et al., 2004; Kwan et al., 2005; Lee et al., 2010).

One interesting approach has been used by Herbst (2004) to predict mill power using DEM and then use it to scale-up the energy-specific breakage rates proposed by Herbst and Fuerstenau (1980) to solve the equation   

$$\frac{\text{d}{w}_i}{\text{d}{\overline{E}}_m}=-S_i^{\text{E}}{w}_i+\sum _{j=1}^{i-1}{S}_j^{\text{E}}{b}_{ij}{w}_j$$(4)

where b_ij is the breakage function back-calculated from batch grinding tests, and Ē_m = Pθ/H is the specific energy, where H is the mill hold-up, θ is the residence time and P is the mill power, estimated using DEM.

The obvious advantage of this approach lies in the fact that DEM captures the influence of liner configuration in mill power, which is not taken into account using power models such as those from Rowland and Kjos (1980). However, in analogy to the traditional population balance models, it does not use distributed collision energy information in predicting mill performance. Further, since the contributions of material and machine are not properly decoupled, this approach becomes significantly more limited when compared to other advanced models of ball mills discussed as follows.

4.2 PBM formulations based on particle bed breakage

One of the first attempts to apply DEM to ball mill modeling was by Rajamani and co-workers at the University of Utah (Rajamani et al., 1993), who described batch grinding using the expression   

$$\frac{\text{d}{M}_i}{\text{d}t}=-\omega \sum _{k=1}^{n}p\left(E_k\right)m_{i,k}+\omega \sum _{j=1}^{i-1}\sum _{k=1}^{n}p\left(E_k\right)m_{j,k}{b}_{ij}\left(E_k\right)$$(5)

where N is the number of collision energy classes, ω is the frequency of collisions, p(E_k) is the fraction of collisions of magnitude E_k, m_i,k is the mass of particles in size interval i broken in a single collision of energy E_k, M_i is the mass of particles in the ith size interval and b_ij(E_k) is the breakage function for jth size interval particles generated from collisions of magnitude E_k.

Rajamani et al. (1993) were able to predict reasonably well the size distribution from grinding limestone in a 25 cm-diameter mill, but only at short grinding times, on the basis of 2D DEM simulations. The limitation of short grinding times was due to the fact that only breakage of the top size fraction was predicted.

This equation, however, does not take into account the instantaneous mass fraction of size i in the mill. This was corrected with the introduction of the term M_i/H as the mass fraction of material contained in size class i, or w_i, in an updated version of the model by Datta and Rajamani (2002), given by

  

$$\frac{\text{d}{w}_i}{\text{d}t}=\frac{\omega }{H}\sum _{k=1}^n\left[p\left(E_k\right)\left(-m_{i,k}{w}_i+\sum _{j=1}^{i-1}{m}_{j,k}{b}_{ij}\left(E_k\right)w_j\right)\right]$$(6)

The model uses information on the broken mass of particles m_i,k at a given collision energy and the energy-specific breakage function, both obtained from drop weight tests with 4-layer particle beds, following the procedure originally proposed by Höfler and Herbst (1990). The broken mass was also described as logarithmic function of the specific collision energy.

The model has been validated by comparisons between measured and calculated size distributions in batch grinding of limestone in mills with diameters from 25 to 90 mm, with reasonable agreement (Datta and Rajamani, 2002). However, a correction factor of 0.8 to both appearance and disappearance terms in Eqn. 6 was needed to fit experimental data. The authors attributed this to the inefficiency of the mill.

Datta and Rajamani (2002) recognized that, in a mill, a particle bed between two colliding balls will be composed of something between a monolayer and several layers of material, and not the 4-layer bed considered in their experiments.

One key limitation of this approach is associated to the fact that it relies heavily on data from breakage of particle beds. This mode of breakage varies as a function of particle size distribution in the bed, impact energy, ball size and number of layers, but covering all these by experiments would be too time-consuming. Indeed, this approach also relies on estimates of broken mass, which are both function of material (type, particle size) and environment (ball size and collision energy), which is not desired for modeling purposes.

The approach by Datta and Rajamani (2002) has been used more recently by Wang et al. (2012) to predict results from batch grinding tests. In this study, the authors compared the type of energy information used in the simulations and also included not only the grinding media in the DEM simulations, but also medium-sized particles to mimic the powder.

The approach reviewed herein assumed that impacts of all energies contribute to breakage, which is not a reasonable assumption since single particle impact tests have shown that a minimum impact energy must be overcome to cause body breakage (Tavares, 2007). Further, particles may sustain damage and become weaker due to impacts that are insufficient to cause outright breakage but may break after a succession of impacts. Finally, this modeling approach does not decouple properly surface from body breakage of ore particles.

4.3 Microscale PBM formulations based on breakage probability

Recognizing the limitations of earlier approaches, some researchers have chosen to use single-particle breakage as the basis of their modeling. The first comprehensive approach along this line has been proposed by King and Bourgeois (1993) and later presented in a modified form by King (2001). It was based on measurements of fracture energies of individual particles (Fig. 3), determined using the impact or ultrafast load cell (Tavares and King, 1998; Tavares, 2007), and on the equivalence between body breakage probability and the fracture energy distribution.

Fig. 3

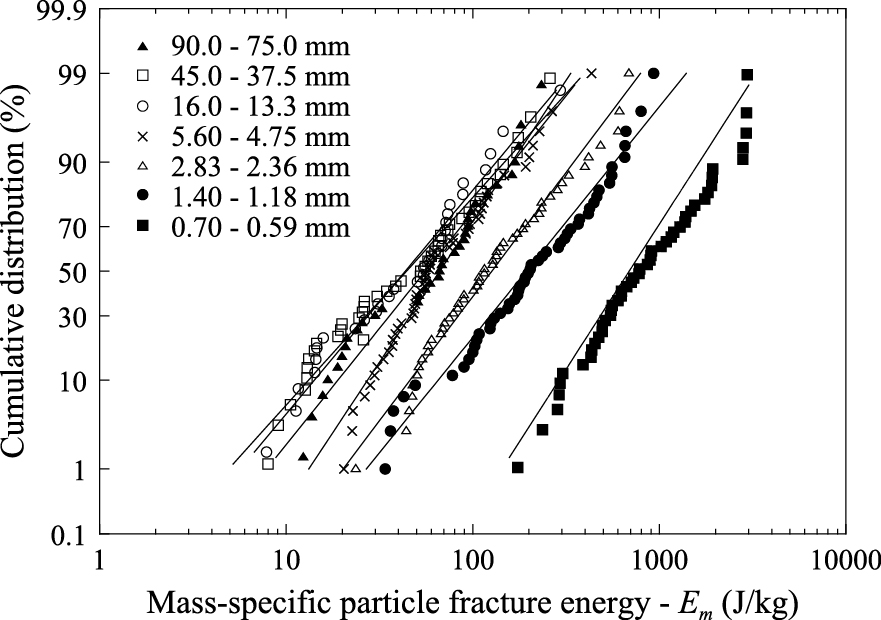
Distribution of particle fracture energies of a gneiss rock over a range of sizes, with a lognormal fit (Eqn. 8). Reprinted with permission from Tavares and Neves (2008). Copyright: (2008) Elsevier Ltd.

King and Bourgeois (1993) accounted for the fact that the following outcomes could occur when a particle is hit by grinding media:

• If the energy is insufficient to cause fracture, the particle will remain intact inside the charge.
• If the energy is sufficient to cause fracture, the particle will undergo primary breakage and rebreakage (secondary breakage), until all energy is dissipated.

The basis of their approach is the postulate that the breakage functions actually effective in the multiparticle environment of a ball mill can be synthesized from the universal single-particle breakage functions once the patterns of energy distribution and stress application are known in a bed of particles that is subject to impact (King and Bourgeois, 1993). The power of this approach is that it avoids the limitations of the particle-bed based approaches, reviewed in section 4.2, that cannot properly cover through experimentation the different bed configurations encountered in practice. On the other hand, one of its limitations is associated to the need for testing single particles at fine sizes, which is both time consuming and inconvenient. Besides that, small sample size statistics can also be considered a limitation of this method (Herbst, 2004).

King (2001) proposed that the breakage rate function of particles contained in size class i could be expressed by   

$$S_i={\int }_0^{\infty }p(E)m_i^{*}(E){\int }_0^1{F}_i(eE)p(e)\text{d}e\text{d}E$$(7)

where p(E) is the distribution of collision energies, estimated using DEM, p(e) is the energy partition amongst particles within the bed, which accounts for the fact that when identical particles are stressed within a bed, they do not necessarily receive the same amount of energy. F_i(eE) is the distribution of fracture energies of particles in size class i, and $m_i^{*}(E)$ is the mass of particles captured in an impact of magnitude E.

King and Bourgeois (1993) demonstrated that the model was able to describe qualitatively the results of batch grinding experiments, but fell short to provide accurate enough descriptions of particle capture and energy split in the bed. They based their predictions on 2D DEM simulations. Nevertheless, this work pioneered the microscale approaches to modeling ball mills.

More recently, Crespo (2011) pursued some aspects of this approach by considering the distribution of particle fracture energies and a perceived distribution of collision energies in a ball mill. While the work demonstrated the capability of his approach of predicting non-first order breakage rates for coarse particles, it suffered from important limitations. Further, it used very simple descriptions of the breakage function, with rather severe simplifications, besides oversimplified descriptions of particle capture probability, which were back-calculated from batch grinding data.

Both of these approaches considered that the distribution of particle fracture energies could be described using the lognormal distribution, which has been demonstrated elsewhere to be able to describe such data properly (King and Bourgeois, 1993; Tavares and King, 1998). It is given by   

$$F_i(E_{\text{m}})=\frac{1}{2}\left[1+\text{erf}\left(\frac{\text{ln}{E}_{\text{m}}-\text{ln}{E}_{\text{m}50,i}}{\sqrt{2{\sigma }^2}}\right)\right]$$(8)

where E_m50,i is the median particle fracture energy and σ² is the variance. The variation of the median fracture energy of the material with particle size could be well described using the expression (Tavares and King, 1998)   

$$E_{\text{m}50,i}=E_{\infty }\left[1+{\left(\frac{d_{\text{o}}}{x_i}\right)}^{\phi }\right]$$(9)

where x_i is the representative size of particles contained in the ith class, E_∞, d_o and φ are model parameters that should be fitted to experimental data. In some cases the variance σ² in Eqn. 8 is also found to vary with particle size and a relationship to describe it has been proposed elsewhere (Carvalho and Tavares, 2013).

A related approach was used by Bwalya et al. (2001) to predict breakage rates in autogenous grinding. The authors considered the distribution of fracture energies of the particles, described with a modified version of the Weichert (1992) breakage probability function derived from single particle breakage in a drop weight tester and collision energies for short grinding times using 2D DEM. Breakage was generally overpredicted compared to an experimental mill, although the model correctly predicted the reduction in breakage rates as a function of particle size. With this approach they were also able to predict the non-first order rates of breakage of coarse particles in a mill.

Another modification of the Weichert (1992) breakage probability function that became very popular was proposed by Vogel and Peukert (2004):   

$$F_i(E_{\text{m}})=1-\text{exp}[-f_{\text{mat}}{x}_i(E_{\text{m}}-E_{\text{m},\text{min}})]$$(10)

where f_mat and x_iE_m,min are constants representing material parameters which should be fit to data, in which E_m,min is the threshold energy, below which particles will not suffer body breakage.

Recently, Tuzcu and Rajamani (2011) proposed another expression for predicting the energy-specific breakage rates for powder in a batch mill on the basis of Eqn. 10, giving   

$$S_i^E=k^{\prime }\omega \sum _{k=1}^{n}p(E_{\text{m},k})F_i(E_{\text{m},k})\frac{E_k}{{\sum }_{k=1}^n{E}_k}$$(11)

which would be used to solve the batch grinding equation   

$$\frac{\text{d}{M}_i}{\text{d}t}=-S_i^{\text{E}}\frac{M_i}{H}+\sum _{j=1}^{i-1}{S}_j^{\text{E}}{b}_{ij}^{\text{E}}\frac{M_j}{H}$$(12)

in which k′ is a constant that includes the captured mass and all other unmodeled effects (Tuzcu and Rajamani, 2011), F_i(E_m,k) is the probability of fracture of particles in size i at the applied specific collision energy E_m,k, described using Eqn. 10. They were able to predict well breakage of coarse particles (top size of 31.8 mm) in a 0.9 m diameter batch mill, using Eqns. 11 and 12 and collision energy spectra from 2D DEM simulations.

Capece et al. (2014) proposed yet another method to calculate the breakage rates, also using Eqn. 10:   

$$S_i=f_{\text{max}}{x}_i\omega \sum _{k=1}^{n}p(E_{\text{m},k})(E_{\text{m},k}-E_{\text{m},\text{min}})$$(13)

where E_m,k is the specific energy in the kth collision. The authors proposed to conduct batch grinding experiments with various narrow-size feeds, then 3D DEM simulations with grinding media and powder particles of these sizes and then fit the material parameters (f_mat, xE_m,min) on the basis of Eqn. 13. The breakage function was back-calculated from data of these batch grinding tests and Eqn. 2. The authors were able to fit one set of material parameters to several experiments with alumina, which demonstrates the relevance of their approach, which circumvents the challenge of estimating the mass of material captured by including the powder particles in the simulations. It has, however, limited predictive capability for finer powder sizes, which are known to be broken in beds and not as individual particles, and for which simulations would require significant computer effort. This approach has similarities to the one proposed by Concas et al. (2006).

Some of the assumptions in these formulations are:

• ii. Approaches of King and Bourgeois (1993), Crespo (2011) and Tuzcu and Rajamani (2011) did not account for the fact that particles that do not break in the impacts become progressively weaker, which significantly affects the chances of particle breakage (Bwalya et al., 2001; Tavares, 2009). As such, the model assumes that the fracture energy distribution of particles contained in a given size class remains unchanged as grinding progresses.
• iii. Essentially all approaches assume that breakage of particles due to abrasion (surface breakage) is negligible and no contribution of shearing of particles during ball-to-ball or ball-to-wall collisions exists.
• iv. The contents of the mill are assumed to be perfectly mixed, that is, the size distribution of the particle bed caught between two colliding balls is the same as the prevailing distribution in the entire mill. This assumption is perceived to be valid for dry grinding where internal classification is not as prevalent as in wet grinding. Bwalya et al. (2001), on the other hand, assumed that the probability of a particle being involved in a collision in a tumbling mill is a function of particle surface area.
• v. The fracture energy or breakage probability of a particle does not vary if it was produced as a progeny of a low-energy or a high-energy stressing event.

By using the breakage probability, these approaches actually included an additional variable to particle size in the population balance model formulation, which is the energy required for (body) breakage, called particle fracture energy.

4.4 Microscale PBM formulations describing different breakage mechanisms

A number of approaches have been proposed that tackle some of the limitations of these earlier models. The commonality amongst them is the fact that they attempt to describe in greater detail the response of the ore or powder to the different fragmentation mechanisms, which could be listed as:

• 1. Body breakage: the integrity of the original particle is completely lost;
• 2. Surface breakage, further described as:
  • a. Attrition or abrasion: mass loss at the surface of rounded rocks as other particles slide over them or they slide over the liner, or as a result of predominantly normal low-energy collisions;
  • b. Chipping: loss of corners, edges and larger asperities from small scale breakage for irregular shaped particles;
  • c. Rounding: preferential and higher abrasive mass loss from sliding at the corners and edges of blocky particles.

The occurrence of either depends on the intensity and mode of stressing. As such, the approaches reviewed in this section also have in common the vision that, since the contributions of the milling environment and of the ore are appropriately decoupled, the same modeling framework can be used to describe different types of comminution machines, and not only tumbling ball mills.

4.4.1 Unified comminution model

This model framework, proposed by Powell et al. (2008) from the University of Cape Town and called unified comminution model (UCM), proposes modeling any size reduction machine by coupling the mechanical environment in the size reduction equipment, obtained using DEM, to data that describes the different fundamental modes of breakage, and tools that characterize the influence of slurry in wet milling, namely CFD and SPH. It employs the population balance framework to mathematically combine the particles and their associated breakage products into a mass balance per time step. For a single component (or material class) and batch operation, it can be expressed as   

$$\frac{\text{d}{M}_i}{\text{d}t}=-\sum _{d=1}^N{\lambda }_i(E_d)M_i-\sum _{r=1}^S{\lambda }_i(E_r)M_i+\sum _{j=1}^{i-1}\left[\sum _{d=1}^N{\lambda }_j(E_d)M_j(E_d)b_{ij}(E_d)+\sum _{r=1}^S{\lambda }_j(E_r)M_j(E_r)b_{ij}(E_r)\right]$$(14)

where λ_i(E) is the net breakage frequency at energy E for the size class i, given by ${\lambda }_i(E)={\lambda }_i^{\text{DEM}}(E)/{\lambda }_i^{\text{exp}}(E)$, in which ${\lambda }_i^{\text{DEM}}(E)$ is the DEM collision frequency at energy E for size class i and ${\lambda }_i^{\text{exp}}(E)$ is the mean number of collisions required to break particles in size class i with collision energy E. N and S are, respectively, the number of normal and shear energy bins and M_i is the mass of material contained in size i in the mill.

The model recognizes that depending on the magnitude of the collision energy on a particle three different outcomes could occur (Powell et al., 2008):

• i. Single hit (body) breakage—for a collision with sufficient energy to break the particle, so that the lower limit for this is defined as E_crit.
• ii. Multiple impact (body) breakage—the energy of a single impact is too low to break the rock, however, as it is hit more times at this energy it has an increasing probability of breakage. As a result of this, the model requires to track the histories of individual particles (Powell and McBride, 2006).
• iii. No bulk damage—the impact energy is too low to cause any bulk damage to the rock. The upper limit for this is defined as E_o.

The strength of the approach is its generality and the fact that it recognizes several of the important “pieces of the puzzle” that were missing in earlier approaches. However, the authors admitted that several voids existed that limited the feasibility of applying the model at the time, including the lack of information on apportioning the energy between colliding media, the left-over energy-input power not accounted for in particle damage and the description of breakage of the sub-DEM material. Several features of the model make it more aligned with requirements of modeling autogenous and semi-autogenous mills than ball mills, since the three different outcomes listed above may only be applicable to ore particles simulated in DEM. It is worth noting that the original approach proposed to describe breakage of sub-DEM particles was acknowledged by the authors to be fairly crude, based on relating energy dissipated in the collisions coupled to the standard Bond ball mill method (Powell et al., 2008).

A first demonstration of a simplified form of the model to calculate breakage rates of a full-scale ball mill has been presented more recently (Powell et al., 2011), although it has not yet been validated for this type of mill.

4.4.2 Virtual comminution machine

Another approach recently proposed in this category is the virtual comminution machine (VCM), by Morrison and Cleary (2008) from the University of Queensland and the CSIRO, respectively. Also meant to be a framework to deal with different size reduction processes, the VCM is the one that has evolved the most in coupling DEM to a description of the slurry flow and discharge classification, given by smoothed particle hydrodynamics (SPH) (Cleary et al., 2006). This approach also had the additional feature of providing a model to describe rounding by means of parameterised super-quadric particles (Cleary and Morrison, 2016) and fines generation by attrition. Further, it also describes weakening by repeated impacts (called incremental breakage by the authors), using the model proposed by Morrison et al. (2007), which is another modification of Eqn. 10 by Vogel and Peukert (2004), given by

  

$$F_i(E_{\text{m}})=1-\text{exp}\left[-b^{··}\sum _{k=1}^n(E_{\text{m}}-f{E}_{\text{o}})\right]$$(15)

If E_m is lower than E_o, the contribution from (E_m – E_o) is zero. b̈ is a material parameter which may contain the particle size i. f is a parameter, characterizing the fraction of E_o at which cracks will stop propagating, which was included in a recent revision of the model to improve fitting to data (Cleary and Morrison, 2016).

It is understood that the model predicts breakage of the sub-DEM material using a population balance approach, although the equations used have not been published by the authors. As such, it is unclear how particle capture of sub-DEM particles is addressed, although recent work in which not only grinding media but also fine particles are included in the simulations sheds light into this (Cleary and Morrison, 2011). Indeed, the researchers recognized that developments that remained to be done included dealing with the presence of fine material in ball mills (Weerasekara et al., 2013).

Many of the capabilities of the model are relatively recent and significant testing and validation is still required to demonstrate the predictive capabilities of the VCM. The developers recognize that good quality characterization of breakage behaviour of the specific rocks being used by all the breakage mechanisms is required and that the VCM is only as good as both its numerical model and ore characterization components (Weerasekara et al., 2013).

Amongst the modelling approaches in the literature of tumbling mills, the VCM is the one that already describes the greatest variety of outcomes from breakage listed in the beginning of this section. Evidently, many of the features of the model, in particular the rounding capability, are particularly suited for predicting size reduction in autogenous and semi-autogenous mills, but would also be useful to predict ball milling with a coarse feed.

4.4.3 Other approaches

Another interesting approach proposed has been to predict breakage by coupling DEM to a tool, called discrete grain breakage (DGB) (Herbst and Potapov, 2004), and computational fluid dynamics (CFD) to describe the slurry flow in the mill. This approach, called High Fidelity Simulation (HFS), attempts to connect single-particle breakage response to mill performance. It has also been proposed as a general approach for predicting different types of crushers and mills, but has been restricted in application to full-scale mills due to the very significant computational effort associated to its use.

More recently, a refinement of the single-particle based approach by King and Bourgeois (1993) was proposed by the author and his research team at the Universidade Federal do Rio de Janeiro (UFRJ). First, the weakening by repeated impacts and the breakage of particles at much lower impact energies is incorporated in the model. In analogy to the other models presented in this section, it also describes surface and body breakage, using (body) breakage probability to distinguish between the two. This model is presented in greater detail in the following section.

Finally, it is worth noting that the approach proposed by Tuzcu and Rajamani (2011) also distinguished body and surface breakage mechanisms, although it described the later in a fairly simplistic manner, assuming a constant proportion of fines produced by this mechanism as grinding time progressed in a batch mill.

4.5 UFRJ mechanistic model

Following the footsteps of the work originally carried out at the University of Utah during the early 1990s (King and Bourgeois, 1993), the research group at UFRJ proposed yet another DEM-based approach to model comminution machines. The model is based on the combination of DEM that is used to describe the mechanical environment in the comminution machine, to a myriad of empirical and semi-empirical models that describe the different breakage modes and that are fitted to particle breakage data, and also to models that describe how sub-DEM particles are captured and how the collision energy is split among particles when they are assembled in beds. These pieces of the puzzle are then put together using two models: the microscale population balance model, which keeps track of the mass balance of particles in each size and ore composition class, and an expression that describes the variation of the distribution of particle fracture energies inside the machine as comminution progresses, called fracture energy convolution. This latter is based on the continuum damage model of particle breakage (Tavares and King, 2002) and the distribution of particle fracture energies (Fig. 3). Both equations will vary according to the mode of operation of the comminution device, if batch or continuous, and also according to the mixing conditions that prevail.

The model considers that when particles suffer an impact, some of them undergo catastrophic (body) breakage and some do not. If stresses are insufficient to cause body breakage, they will undergo surface breakage (abrasion/chipping) and will also become progressively weaker.

The batch grinding process equation can be derived from a more general formulation of the traditional population balance model applied to the microscale description of size reduction processes (Carvalho and Tavares, 2009). The equation that describes the rates of changes in mass of material contained in size class i is   

$$\begin{array}{l}\frac{\text{d}{w}_i}{\text{d}t}=\frac{\omega }{H}\{-w_i{\int }_0^{\infty }{m}_i^{*}(E)p(E){\int }_0^1\left[1-b_{ij}(eE)\right]\hspace{0.17em}{F}_i(eE,t)p(e)\text{d}e\text{d}E\\ +\sum _{j=1}^{i-1}{w}_j{\int }_0^{\infty }{m}_j^{*}(E)p(E){\int }_0^1{b}_{ij}(eE)F_j(eE,t)p(e)\text{d}e\text{d}E\\ -D_{i,\text{s}}(t)+A_{i,\text{s}}(t)\}\end{array}$$(16)

where H is the powder or ore load, also called mill hold-up, w_i is the mass fraction of particles contained in size class i in the mill at time t, ω is the frequency of stressing events, p(E) is the distribution of stressing energies E in the mill, $m_i^{*}(E)$ is the mass of particles contained in size class i captured in each collision event of magnitude E and p(e) is the function that represents the energy split among particles nipped in a bed. b_ij(eE) is the body breakage function in density form, dependent on stressing energy (Tavares and Carvalho, 2009) and A_i,s and D_i,s are functions that characterize the appearance and disappearance due to surface breakage, omitted for brevity, and presented elsewhere (Carvalho and Tavares, 2013). The product eE is the fraction of the collision energy that is absorbed by each particle captured in an impact event.

The body breakage function is described on the basis of expressions that account for the effect of particle size and stressing energy on the size distribution of the progeny fragments. The reduction in size of the progeny with increasing applied energy has been described very successfully using the t₁₀-procedure. The size distribution from impacts at a specific energy E_m on particles contained in size class j is calculated by first estimating the fraction of material passing 1/10^th of the original particle size, called t₁₀, using the expression (Tavares, 2009)   

$$t_{10,j}=A\left[1-\text{exp}\left(-b^{\prime }\frac{E_{\text{m}}}{E_{\text{m}50b,j}}\right)\right]$$(17)

where A and b′ are model parameters and E_m50b,j is the median mass-specific particle fracture energy of the particles that are broken as a result of an impact of magnitude E_m. When the collision energy is higher than the fracture energy of the toughest particle contained in size class j, then E_m50b,j = E_m50,j, otherwise it should be calculated numerically (Tavares and Carvalho, 2009). The validity of Equation (17) has been demonstrated elsewhere (Tavares, 2009).

From the t₁₀ value, calculated using Eqn. 17, it is then possible to estimate the proportions passing (t_n values) of different fractions of the original parent size for each collision energy and particle size investigated. This is done with the aid of a model that is based on the incomplete beta function (Carvalho and Tavares, 2013). The cumulative breakage function is then calculated from B_ij(E_m) = interp(t₁₀, t_n).

In the case of batch operation, Eqn. 16 should be solved simultaneously with the equation that describes how the fracture probability distribution of particles contained in each size i varies with time, given by   

$$F_i(E,t+\mathrm{\Delta }t)=\frac{G_i{F}_i^{*}(E,t+\mathrm{\Delta }t)+H_i{F}_i(E,0)+I_i{F}_i(E,t)}{G_i+H_i+I_i}$$(18)

where G_i is the fraction of material in the size class that has been damaged but remained in the original size range, H_i is the fraction that appeared due to body and surface breakage, and I_i is the fraction that was not captured in the time interval, with expressions given elsewhere (Carvalho and Tavares, 2013).

The fracture probability distribution of the original material F_i(E, 0) can be, generally, described well using the lognormal distribution, given by Eqn. 8. In some cases, an upper truncation of the distribution is also necessary (Carvalho and Tavares, 2013). The median particle fracture energy varies according to size through Eqn. 9, and E_50,i = E_m50,i m̄_p,i. The mean weight of a particle contained in size class i may be estimated by ${\overline{m}}_{\text{p},i}=\rho \beta x_i^3$, where ρ is the material specific gravity and β the volume shape factor.

Also, the standard deviation of the lognormal distribution of particle fracture energies (Eqn. 8) can vary with size and the variation can be described using an expression analogous to Eqn. 9 (Carvalho and Tavares, 2013).

In Eqn. 18 F_i(E, t) is the distribution of fracture energies of the material contained in size class i that did not suffer any impact event during the time interval, whereas $F_i^{*}(E,t+\mathrm{\Delta }t)$ is the distribution of fracture energies of the particles in size class i that were captured in a collision event, but did not fracture, being given by the convolution equation   

$$F_i^{*}(E,t+\mathrm{\Delta }t)=\frac{{\int }_0^{E_i^{*}}p(E^{\prime }){\int }_0^1\left\{\frac{F_i[E/(1-D),t]-F_i(e{E}^{\prime },t)}{1-F_i(e{E}^{\prime },t)}\right\}p(e)\text{d}e\text{d}{E}^{\prime }}{{\int }_0^{E_i^{*}}p(E^{\prime })\text{d}{E}^{\prime }}$$(19)

and   

$$D={\left[\frac{2\gamma (1-D)}{(2\gamma -5D+5)}\frac{e{E}^{\prime }}{E}\right]}^{\frac{2\gamma }{5}}$$(20)

where $E_i^{*}$ is the maximum fracture energy of particles contained in class i, which is equal to the value that satisfies $F_i(E_i^{*})=1$ as comminution progresses (Tavares and Carvalho, 2009) and γ is a parameter that characterizes the amenability of the material to breakage by repeated impacts, which is typically independent of particle size (Tavares, 2009). The model is able to account for the fact that particles that are stressed but do not fracture in a collision event will become progressively weaker. The model does not have an explicit damage threshold, since the amount of damage sustained by particles becomes progressively smaller as the ratio between the collision energy (eE′) and their fracture energy (E) approaches zero.

Illustration of application of Eqns. 18 to 20 to material ground in a batch mill (Fig. 4) demonstrates the progression of the distribution of fracture energies of the remaining material in the top size range. It shows the predominant effect of survival of the toughest particles, along with the weakening of a fraction of the population of the particles.

Fig. 4

Predicted variation of particle fracture energies of 9.5 × 6.3 mm granulite particles with grinding time in a 0.3 m diameter batch mill with 25 mm steel balls, 67 % of critical speed and 30 % mill filling. Reprinted with permission from Tavares and Carvalho (2009). Copyright: (2009) Elsevier Ltd.

The mass of material captured ( $m_i^{*}$) between two grinding media elements may be estimated from the product of the number of particles caught between the two grinding media (N_cap,i) and the average weight of the particles (m̄_p,i), $m_i^{*}={\overline{m}}_{\text{p},i}{N}_{\text{cap},i}$.

Given the evidence from earlier work (Höfler, 1990), that particles in an unconfined bed normally only break when they are typically squeezed down to one or two layers between grinding media, particles are modeled as a packed monolayer bed. If particles had spherical shapes, and if they were arranged according to a dense hexagonal packing, then the number of particles captured as a function of radius from the center of impact could be estimated by (Barrios et al., 2011a)   

$$\begin{array}{lll}{N}_{\text{cap},i}\hfill & =\frac{1}{4}+\frac{3}{4}{\left(\frac{2r_{\text{c}}}{x_i}\right)}^2\hfill & \text{for\hspace{0.17em}}{r}_{\text{c}}\ge x_i/2\hfill \\ \hspace{0.17em}\hfill & =1\hfill & \text{for\hspace{0.17em}}{r}_{\text{c}}<x_i/2\hfill \end{array}$$(21)

where r_c is the radius of the bed, also called radius of capture, and x_i is the mean size of the particles caught by the colliding steel ball, estimated from the geometric mean of sieves sizes containing the fraction.

A model has been proposed by Barrios et al. (2011a) to calculate this radius of capture on the basis of diameters of colliding grinding media, size of particles, their strength and impact energies. An illustration of the effect of impact energy and particle size on the radius of capture is presented in Fig. 5. This model has also been used by other researchers (Powell et al., 2011) to estimate mass captured of sub-DEM material in mill simulations. The validity of the model in describing the mass of material captured and the energy distribution in the bed inside the milling environment, however, has not yet been demonstrated, but is the subject of ongoing work in the author’s laboratory.

Fig. 5

Radius of capture in the contact between balls of different sizes and a monolayer bed of particles contained in the size range sitting on a flat anvil for different particle sizes and impact energies. Symbols present experiments and lines the model fit. Reprinted with permission from Weerasekara et al. (2013). Copyright: (2013) Elsevier Ltd.

In the description of the energy split function in the bed p(e), it is considered that the stressing energy is split equally among particles positioned in the bed, so that p(e) = δ(e – 1/N_cap,i), where δ is the Dirac delta function. However, another more complex expression has also been proposed to describe the energy split in a more realistic way (Barrios et al., 2011a).

The size-discretized Equations (16) and (18) are solved simultaneously at each time step using a finite difference scheme. Time steps are typically in the order of 0.01 s, but should be chosen to be as small as necessary to guarantee that particles take part in no more than one collision event in the interval.

The sensitivity of the model to the geometry of the impact makes it worthwhile to log separately collisions between each two elements in contact, forming a matrix of probability distributions of collision energies.

The model has demonstrated to be capable of predicting non-first order breakage rates of coarse particles (Tavares and Carvalho, 2009) and also of describing the effects of several design and operating variables in milling in breakage rates (Carvalho and Tavares, 2013). The effect of ball size on specific breakage rates predicted using the model is illustrated in Fig. 6, and shows that the model is capable of accounting for the shift in the size corresponding to the maximum breakage rate with a change in ball size, which has been widely documented in the literature (Austin et al., 1984; Katubilwa and Moys, 2009). Smaller ball sizes produce less energetic impacts and each impact captures fewer particles, being also less efficient at nipping coarser particles. Offsetting these effects that tend to decrease the specific rate of breakage as ball size decreases is the increased frequency of impacts that results from the larger number of smaller balls in the mill, also shown in the figure.

Fig. 6

Simulated breakage rates for a copper ore as a function of particle and steel ball size for a ball mill (top) and DEM median impact energy and collision frequency as a function of ball size (bottom), where M_b is the mass of the ball charge (30 % mill filling and 67 % of critical speed in a 0.3 m diameter mill). Reprinted with permission from Carvalho and Tavares (2013). Copyright: (2013) Elsevier Ltd.

Additional work has demonstrated that grinding of multi-component mixtures in continuous mills can also be simulated using the model (Carvalho and Tavares, 2009), although the validity of the predictions has not yet been demonstrated. Detailed model validation is underway in the authors laboratory (Rodriguez, 2016), and Fig. 7 illustrates results that demonstrate that the model can predict batch grinding well even at prolonged times.

Fig. 7

UFRJ mechanistic model validation in dry batch grinding of granulite. Symbols are experimental data and lines model predictions (0.3 m mill, 40 mm steel balls, 30 % filling, 100 % interstitial filling, 67 % of critical speed).

Unlike the UCM and the VCM, the mechanistic mill model describes single hit breakage and incremental breakage with no distinction, since it accounts for the distribution of fracture energies of the material and uses Eqn. 17 to characterize intensity of breakage in both cases. As such, it is truly a two-variable model, since not only sizes of particles change as grinding progresses, but also their fracture energies.

Besides considering the assumptions i, iv, and v of the earlier single-particle based models (4.3), the UFRJ mechanistic mill model does not yet account for the interaction of particles of different sizes in the bed, in spite of evidences that this has been found relevant in the past (Schönert, 1979).

5. Discussion

5.1 Fracture probability distributions

Several approaches reviewed require information on fracture probability distributions and their variation with particle size. Different models (Tavares and King, 1998; Vogel and Peukert, 2004; Rozenblat et al., 2012) have been proposed to describe this variation. Several authors (King and Bourgeois, 1993; Tavares and Carvalho, 2009; Crespo, 2011) used the lognormal distribution (Eqn. 8) and the relationship describing the variation of the median fracture energy with size given by Eqn. 9, which have demonstrated to be capable of describing material response over a range of sizes (Tavares and King, 1998; Tavares and Neves, 2008).

The approach proposed by Vogel and Peukert (2004) and the Weibull distribution has attracted significant attention, being used, either directly or modified, in describing breakage probability in several approaches (Concas et al., 2006; Morrison and Cleary, 2008; Tuzcu and Rajamani, 2011; Capece et al., 2014), in particular owing of its simplicity, with only two fitting parameters. This model (Eqn. 10) identifies a threshold collision energy below which no body breakage would occur. Although the model has explicitly the number of impacts, so that it can describe weakening by repeated impacts, a more appropriate modification has been proposed by Morrison et al. (2007) that more appropriately describes this effect.

As such, given its popularity, it is important to analyze the approach of Vogel and Peukert (2004) in greater detail. Solving Eqn. 10 considering the case in which particles are impacted at exactly their median fracture energy, so that F_i(E_m50) = 0.5 in Eqn. 10, gives   

$$E_{\text{m}50,i}=x_i{E}_{\text{m},\text{min}}\left[1+\left(\frac{k^{″}}{x_i}\right)\right]$$(24)

where k″ = ln(2)/f_matx_iE_m,min.

The similarity between Equations (24) and (9) is evident, with the key difference that the median fracture energy is inversely proportional to particle size in Eqn. 24 (–1 power), whereas it was found to vary, according to material, from –0.8 to about –2.5 for geological materials (Tavares and King, 1998; Tavares and Neves, 2008). As such, the model given by Eqns. 9 and 10 provides not only a more realistic description of the variation of breakage probability with size but also allows decoupling the variability in the breakage probability distributions from the effect of size in the median fracture energy. It has, however, more parameters (four in total, in contrast to only 2 in Eqn. 10) that need to be fitted from experimental data on breakage probability or fracture energy distributions for a range of sizes. This data can be collected with reasonable convenience at intermediate and coarse sizes (Dan and Schubert, 1990; Tavares and King, 1998; Rozenblat et al., 2012) but no robust solution appeared yet to deal with breakage of fine particles, although some alternatives have been proposed (Marktscheffel and Schönert, 1986; Barrios et al., 2011b; Ribas et al., 2014). Nevertheless, Eqn. 10 can be a good compromise between complexity and capability to describe reality for using in earlier stages of development of advanced models of milling, in particular when the model developer has little access to data on particle breakage probability.

5.2 Collision energies

As discussed earlier, at least three options exist in regard to the collision energies from DEM for advanced mill simulations. It is, however, important to match the information on the collision that is obtained in DEM with the information from single-particle breakage (Powell et al., 2008). For instance, not all energy involved in a collision is absorbed by individual particles and/or a bed, leading to a rebound that could lead to additional breakage.

Several researchers (Datta and Rajamani, 2002; Tavares and Carvalho, 2009; Capece et al., 2014) use the dissipated energies as the basis of their simulations. Using the model approach and data by Datta and Rajamani (2002), Wang et al. (2012) concluded that the kinetic energies in the collision were the type of information that could most reliably predict the batch mill performance. The use of the dissipated energy is considered valid in the UFRJ Mechanistic Model since the energies that are used to model fracture probabilities (Eqn. 8) and energy-specific breakage function (Eqn. 18) already account only the absorbed by the particles (Tavares, 1999). However, the authors recognize a mismatch can occur between the sum of dissipated energy and the total energy computed by the center of gravity of the charge, in particular as mill diameters increase (Carvalho and Tavares, 2013).

Normal and shear components of the collisions contribute to breakage and should be considered in the model predictions. Indeed, these appear explicitly in the UCM equations (Powell et al., 2008) and are used actively to describe the different outcomes of breakage as part of the VCM (Morrison and Cleary, 2016). Other authors (Datta and Rajamani, 2002; Tuzcu and Rajamani, 2012) simply group the two components and deal with the combined spectrum. However, the actual roles of normal and shear components in the different modes of breakage are not yet entirely clear (Powell and McBride, 2006), in particular when dealing with surface breakage. Originally the UFRJ model only used the normal components of the collision (Tavares and Carvalho, 2009), but the latest version of the model, with an improved description of surface breakage, also includes the shear component (Rodriguez, 2016).

5.3 Other

Simulations using the discrete element method have been used to investigate mixing between grinding media and ore charge. Cleary and Morrison (2011) included powder at different proportions to investigate its effect on the motion of charge and collision spectra in a laboratory ball mill. They showed that particles were not uniformly distributed, but tended to concentrate at the shoulder region at very low powder fillings. At higher powder fillings, namely above 100 %, mixing between grinding media and powder was good, thus justifying the approximation used in nearly all the advanced models. The only model that does not explicitly consider this assumption is the VCM (Morrison and Cleary, 2008), although outcomes from relaxing this assumption have not yet been presented.

One of the first observations from DEM simulations of mills is that the frequency of high-energy impacts, such as those reproduced in standard drop weight tests (Napier-Munn et al., 1996) is very small, shedding light into the importance of low-energy collisions and, therefore, to weakening by repeated impacts and to surface breakage. Whereas the former has attracted significant attention (Tavares and King, 2002; Morrison et al., 2007), descriptions of surface breakage are still in their infancy, in particular if compared to volume breakage. In spite of some recent worthwhile attempts (Morrison and Cleary, 2008; Yahyei et al., 2015), a need exists to study this mode of breakage in greater detail in the future to properly inform advanced mill models. Indeed, it is important to recognize that surface breakage can be understood as either the result of normal collisions that are of insufficient magnitude to cause body breakage (Tavares and Carvalho, 2009), or to collisions that are predominantly of the shear type, although this distinction is seldom made by researchers. The lack of proper descriptions and understanding of breakage by either pure or predominant shear have so far prevented its implementation in the UFRJ mechanistic model (Carvalho and Tavares, 2013).

Nearly all advanced approaches use some form of population balance framework to mathematically combine the particles and their associated breakage products into a mass balance per time step. Several of the approaches (King, 2001; Datta and Rajamani, 2002; Capece et al., 2014) use the linear population balance model equation, e.g., Eqn. 2 in the case of the batch mill, with the only difference that breakage and selection functions are calculated on the basis of data from DEM simulations. Other approaches (King and Bourgeois, 1993; Tavares and Carvalho, 2009) use a different formulation of the population balance model equations, called microscale population balance model, since breakage mechanisms and collision energy spectra are convoluted in the equations. Amongst the approaches that consider the breakage probability (fracture energies), only the UFRJ Mechanistic Model (Tavares and Carvalho, 2009) addresses its change as the result of both breakage of particles and weakening of the unbroken particles. Indeed, this model can be, potentially, used to predict the fracture energies of particles that leave the mill, which can impact downstream processes.

Models differ even at the most fundamental level of definition of body breakage. Whereas several follow the definition used in all traditional population balance model formulations of breakage as departure from the original size range that contains the particle (Datta and Rajamani, 2002; Capece et al., 2014), other formulations (King and Bourgeois, 1993; Tavares and Carvalho, 2009) consider breakage as the loss of a substantial part of the particle weight, taken arbitrarily as 10 % (Dan and Schubert, 1990). As such, it accounts for the fact that when a particle suffers body breakage, fragments from it can remain in the original size range.

It is evident from this review that very important advances have been made, in particular in the last 10 years, in advanced ball mill modeling. The approaches that are progressing further are those that account for breakage probability and also that distinguish the different breakage mechanisms. However, important challenges remain, in particular related to connecting single particle breakage response at fine sizes to milling response, both batch and continuous, and to modeling surface breakage. It is the opinion of the author that it will reach maturity in the next several years, following on the footsteps of other already mature applications of DEM, such as in transfer chute design and liner design for preventing ultraprojection of grinding media.

6. Conclusions

• • Several approaches have been proposed since the late 1980s to describe beyond mean breakage rates, breakage functions and specific comminution energy, size reduction in tumbling mills.
• • Since the 1990s these approaches evolved significantly, given the contribution of the discrete element method (DEM) in describing the mechanical environment in mills.
• • In spite of the increase in computing power, modeling ball mills is still better described considering only the grinding charge and not the powder in the DEM simulations, relaying on post-processing the data using a proper population balance formulation to predict grinding.
• • Several of the initial approaches in advanced modeling relied exclusively on particle bed data to describe breakage. In spite of their simplicity, they became less popular given the lack of description of breakage probability and also the difficulty of representing all combinations that would be found in practice.
• • Models that rely on single particle breakage and (body) breakage probability have gained popularity in recent years and were pioneered by the work of King and Bourgeois (1993). The approaches differ by the expressions used to describe breakage probability. Several of these models have adopted the formulation of Vogel and Peukert (2004), although more flexible alternatives exist.
• • A limited number of approaches decouple body and surface breakage, and only one approach (VCM) describes explicitly rounding of coarse particles due to surface breakage, which could be relevant in ball milling of oversized feeds.
• • A very limited number of approaches account for weakening by repeated unsuccessful collisions.
• • The approach proposed in the author’s laboratory describes how breakage probability varies due to breakage and weakening of the particles. This approach also includes sub-models that successfully describe the different mechanisms (body and surface breakage, but not rounding), as well as the mass of powder captured in each collision, besides efficient solution algorithms that have been used to predict grinding over a range of conditions. As such, this is the only two-variable model, in which the material can change not only its size class, but also its fracture energy as grinding progresses.
• • The important progress in recent years suggests advanced models of ball mills will reach some level of maturity in upcoming years.

Nomenclature

A

model parameter of Eqn. 17

A_i,s

function describing birth by surface breakage

b′

model parameter of Eqn. 17

b″

parameter of Eqn. 15

B_ij

cumulative body breakage function

b_ij

body breakage function in density form

B_ij(E_m,k)

cumulative energy-specific breakage function for jth size interval

b_ij(E_m,k)

energy-specific breakage function in density form for jth size interval

D

damage sustained by a particle

D_i,s

disappearance function for surface breakage

d_o

parameter in Eqn. 9

e

variable representing the fraction of the collision energy absorbed by a particle

E

collision energy

E′

collision energy (integration variable)

E_crit

lowest magnitude of collision energy required to break a particle

$E_i^{*}$

maximum fracture energy of particles contained in class i

E_k

impact energy in kth collision or mean collision energy in kth class

E_m

specific collision energy

Ē_m

mean specific comminution energy

E_m,k

specific energy in the kth collision or mean collision energy in kth class

E_m,min

parameter in Eqn. 10, which represents the threshold specific energy for body breakage

E_m50,i

median mass-specific particle fracture energy of particles in size class i

E_m50b,i

median fracture energy of particles in size class i that are broken as a result of impact of magnitude E_m

E_n

normal portion of the collision energy

E_o

parameter of Eqn. 15, representing the energy below which particles do not fracture erf error function

E_s

shear portion of the collision energy

E_50,i

median particle fracture energy of particles in size class i

E_∞

parameter in Eqn. 9, representing the median fracture energy of infinitely coarse particles

f

parameter of Eqn. 15, characterizing the fraction of E_o in which cracks will stop propagating

F_i(E,0)

fracture probability distribution of the original material in size class i

F_i(E_m)

fracture probability distribution of particles contained in size i at a specific collision energy E_m

$F_i^{*}(E,t)$

distribution of fracture energies of the particles in size class i that were captured in an impact event, but did not fracture

f_mat

parameter in Eqn. 10

F_n

normal component of the contact force

F_s

shear component of the contact force

G_i

fraction of material in size class i that has been damaged but remained in the original size range

H

powder or ore load, also called mill hold-up

H_i

fraction of material that appeared in size class i due to body and surface breakage

I_i

fraction of material that in size class i was not captured in the time interval

k′

constant in Eqn. 11

k″

constant in Eqn. 24

M_b

mass of the ball charge

m_b

mass of one grinding medium or reduced mass in a collision

m_b.i

mass of ith ball in a collision

M_i

mass of particles in the ith size interval

m_i(E)

broken mass of particles in size class i resulting from an impact of magnitude E

$m_i^{*}(E)$

mass of particles contained in size class i captured in each stressing event of magnitude E

m̄_p,i

mean weight of a particle contained in size class i

N

number of normal collision energy bins

n

number of collision energy bins

N_cap,i

number of particles contained in size class i captured in a collision event

P

mill power predicted by DEM

P(E)

cumulative distribution of collision energies

p(E)

distribution of collision energies in density form

p(e)

energy split among particles in each collision

p(E_m,k)

distribution of specific collision energies in density form

r_c

radius of capture of the bed

S

number of shear collision energy bins

S_i

selection or breakage rate of particles in size i

$S_i^{\text{E}}$

energy-specific selection function

t

time

t_contact

total contact time during a collision

t_n

fraction of material body broken to 1/n^th of the parent size

t₁₀

fraction of material body broken to 1/10^th of the parent size

v_i

velocity of grinding medium i in a collision

v_ij

relative velocity of grinding media i and j

w_i(t)

mass fraction of particles contained in size class i in the mill at time t

x

particle size

x_i

mean size of particles in size class i

Greek symbols

β

volume shape factor

γ

damage accumulation parameter (Eqn. 20)

δ

Dirac delta function

θ

mean residence time

λ_i(E)

net breakage frequency at energy E for the size class i

${\lambda }_i^{\text{DEM}}(E)$

DEM collision frequency at energy E for size class i

${\lambda }_i^{\text{exp}}(E)$

mean number of collisions required to break the particle with collision energy E

ξ

deformation of media during a collision

ρ

specific gravity

σ

standard deviation of the log-normal distribution of particle fracture energy (Eqn. 8)

φ

parameter in Eqn. 9

ω

frequency of collisions

Author’s short biography

Luís Marcelo Tavares

Luís Marcelo Tavares is a Professor at the Department of Metallurgical and Materials Engineering of Universidade Federal do Rio de Janeiro. He received his bachelor’s degree in Mining Engineering (honours) and his master’s degree from Universidade Federal do Rio Grande do Sul. In 1997 he was awarded a Ph.D. degree in Extractive Metallurgy at the University of Utah under the supervision of the late Professor R.P. King. He has been a member of the faculty of the Universidade Federal do Rio de Janeiro (Brazil) since 1998, where he is head of the Laboratório de Tecnologia Mineral and has been Department chairman. His research interests include advanced models of comminution, particle breakage, physical concentration, classification, iron ore processing and development of pozzolanic materials. He is a founding member of the Global Comminution Collaborative (GCC) and has received a number of awards from the Brazilian Association of Metallurgy, Materials and Mining (ABM).

References

•  Austin  L.G.,  Klimpel  R.R.,  Luckie  P.T., Process engineering of size reduction, AIME, New York, 1984.
•  Barrios  G.K.P.,  Carvalho  R.M.  de Tavares  L.M., Modeling breakage of monodispersed particles in unconfined beds, Minerals Engineering, 24 (2011a) 308–318.
•  Barrios  G.K.P.,  Carvalho  R.M.  de Tavares  L.M., Extending breakage characterisation to fine sizes by impact on particle beds, Transactions of the Institution of Mining and Metallurgy C, 120 (2011b) 37–44.
•  Barrios  G.K.P.,  Tavares  L.M., A preliminary model of high pressure roll grinding using the discrete element method and multi-body dynamics coupling, International Journal of Mineral Processing (2016), doi: 10.1016/j.minpro.2016.06.009.
•  Bond  F.C., The third theory of comminution, Transactions of AIME, 193 (1952) 484–494.
•  Bwalya  M.M.,  Moys  M.H.,  Hinde  A.L., The use of discrete element method and fracture mechanics to improve grinding rate prediction, Minerals Engineering, 14 (2001) 565–573.
•  Capece  M.,  Bilgili  E.,  Davé  R.N., Formulation of a physically motivated specific breakage rate parameter for ball milling via the discrete element method, AiChe Journal, 60 (2014) 2404–2415.
•  Carvalho  R.M.,  Tavares  L.M., Dynamic modeling of comminution using a general microscale breakage model. Computer-Aided Chemical Engineering, 27 (2009) 519–524.
•  Carvalho  R.M.,  Tavares  L.M., Predicting the effect of operating and design variables on breakage rates using the mechanistic ball mill model, Minerals Engineering, 43–44 (2013) 91–101.
•  Chagas  A.S.,  Carvalho  R.M.,  Bbosa  L.,  Mainza  A.,  Tavares  L.M., Calibration of DEM contact parameters for tumbling mills using PEPT. Proceedings, 14th European Symposium on Comminution and Classification, Gothenburg, 2015, pp. 1–6.
•  Charles  R.J., Energy-size reduction relationships in comminution, Transactions of the AIME, 208 (1957) 80–88.
•  Cho  H., Breakage mechanisms in size reduction, Ph.D. thesis, University of Utah, 1987.
•  Cleary  P.W., Predicting charge motion, power draw, segregation wear and particle breakage in ball mills using discrete element methods, Minerals Engineering, 11 (1998) 1061–1080.
•  Cleary  P.W., Recent advances in DEM modeling of tumbling mills, Minerals Engineering, 14 (2001) 1295–1319.
•  Cleary  P.W.,  Sinnott  M.,  Morrison  R.D., Prediction of slurry transport in SAG mills using SPH fluid flow in a dynamic DEM based porous media, Minerals Engineering, 19 (2006) 1517–1527.
•  Cleary  P.W.,  Morrison  R.D., Understanding fine ore breakage in a laboratory scale ball mill using DEM, Minerals Engineering, 24 (2011) 352–366.
•  Cleary  P.W.,  Morrison  R.D., Comminution mechanisms, particle shape evolution and collision energy partitioning in tumbling mills, Minerals Engineering, 86 (2016) 75–95.
•  Cleary  P.W.,  Sinnott  M.D., Simulation of particle flows and breakage in crushers using DEM: Part 1—Compression crushers, Minerals Engineering, 74 (2015) 178–197.
•  Concas  A.,  Lai  N.,  Psiu  M.,  Cao  G., Modelling of comminution processes in Spex mixer/mil, Chemical Engineering Science, 61 (2006) 3746–3760.
•  Crespo  E.F., Application of particle fracture energy distributions to ball milling kinetics, Powder Technology, 210 (2011) 281–287.
•  Dan  C.C.,  Schubert  H., Breakage probability, progeny size distribution and energy utilization of comminution by impact, Aufbereitungs-Technik, 31 (1990) 241–247.
•  Datta  A.,  Rajamani  R.K., A direct approach of modeling batch grinding in ball mills using population balance principles and impact energy distribution, International Journal of Mineral Processing, 64 (2002) 181–200.
•  Delaney  G.W.,  Cleary  P.W.,  Morrison  R.,  Loveday  B., Predicting breakage and the evolution of rock size and shape distributions in Ag and SAG mills using DEM, Minerals Engineering, 50–51 (2013) 132–139.
•  Govender  I.,  Cleary  P.W.,  Mainza  A.N., Comparisons of PEPT derived charge features in wet milling environments with a friction-adjusted DEM model, Chemical Engineering Science, 97 (2013) 162–175.
•  Herbst  J.A., A microscale look at tumbling mill scale-up using high fidelity simulation, International Journal of Mineral Processing, 74S (2004) S299–S306.
•  Herbst  J.A.,  Fuerstenau  D.W., Scale-up procedure for continuous grinding mill design using population balance models, International Journal of Mineral Processing, 7 (1980) 1–31.
•  Herbst  J.A.,  Potapov  A.V., Making a discrete grain breakage model practical for comminution equipment performance simulation, Powder Technology, 143–144 (2004) 145–150.
•  Höfler  A., Fundamental breakage studies of mineral particles with an ultrafast load cell device, Ph.D. thesis, University of Utah, 1990.
•  Höfler  A.,  Herbst  J.A., Ball mill modeling through microscale fragmentation studies: fully monitored particle bed comminution versus single impact tests, Proceedings, 7th European Symposium on Comminution, Ljubluana, 1990, v. 1, pp. 381–397.
•  Kano  J.,  Saito  F., Correlation of powder characteristics of talc during planetary ball milling with the impact energy of the balls simulated by the particle element method, Powder Technology, 98 (1998) 166–170.
•  Katubilwa  F.M.,  Moys  M.H., Effect of ball size distribution on milling rate, Minerals Engineering, 22 (2009) 1283–1288.
•  Kick  F., Des Gesetz der Proportionalem wider-stand und Seine Anwendung, Felix, Leipzig, 1885.
•  King  R.P., Modeling and simulation of mineral processing systems, Butterworth-Heinemann, 2001.
•  King  R.P.,  Bourgeois  F.S., A new conceptual model for ball milling. Proceedings, 18th International Mineral Processing Congress, Sydney, 1993, pp. 81–86.
•  Kwan  C.,  Mio  H.,  Chen  Y.,  Ding  Y.,  Saito  F.,  Papadopoulos  D.,  Bentham  A.,  Ghadiri  M., Analysis of the milling rate of pharmaceutical powders using the distinct element method (DEM), Chemical Engineering Science, 60 (2005) 1441–1448.
•  Lee  L.,  Cho  H.,  Kwon  J., Using the discrete element method to analyze the breakage rate in a centrifugal/vibration mill, Powder Technology, 198 (2010) 364–372.
•  Marktscheffel  M.,  Schönert  K., Liberation of composite particles by single particle compression, shear and impact loading, Proceedings, 6th European Symposium on Comminution, Nuremberg, 1986.
•  Martins  S.,  Li  W.,  Radziszewski  P.,  Faucher  A.,  Makni  S., Experimental and simulated ball in a tumbling mill—a comparison, Minerals Engineering, 43–44 (2012) 79–94.
•  Mayank  K.,  Narasimha  M.,  Govender  I., Two way coupled CFD-DEM model to predict tumbling mil dynanics, Proceedings, International Semi-Autogenous Grinding and High-Pressure Roll Grinding Technology, Vancouver, 2015, paper #28.
•  Metzger  M.J.,  Glasser  B.J., Simulation of the breakage of bonded agglomerates in a ball mill, Powder Technology, 237 (2013) 286–302.
•  Mishra  B.K.,  Murty  C.V.R., On the determination of contact parameters for realistic DEM simulations of ball mills, Powder Technology, 115 (2001) 290–297.
•  Mishra  B.K.,  Rajamani  R.K. The discrete element method for the simulation of ball mills, Applied Mathematical Modeling, 16 (1992) 598–604.
•  Morrell  S., An alternative energy–size relationship to that proposed by Bond for the design and optimisation of grinding circuits, International Journal of Mineral Processing, 74 (2004) 133–141.
•  Mori  H.,  Mio  H.,  Kano  K.,  Saito  F., Ball mill simulation in wet grinding using a tumbling mill and its correlation to grinding rate, Powder Technology, 143–144 (2004) 230–239.
•  Morison  R.D.,  Cleary  P.W., Towards a virtual comminution machine, Minerals Engineering, 21 (2008) 770–781.
•  Morrison  R.D.,  Shi  F.,  Whyte  R., Modelling of incremental rock breakage by impact—For use in DEM models, Minerals Engineering, 20 (2007) 303–309.
•  Moys  M.H.,  van Nierop  M.A.,  van Tonder  J.C.,  Glover  G., Validation of the discrete element method (DEM) by comparing predicted load behavior to a grinding mill with measured data, Developments in Mineral Processing, Elsevier, 2000, v. 13, pg. C3-39–C3-44.
•  Napier-Munn  T.J.,  Morrell  S.,  Morrison  R.D.,  Kojovic  T., Mineral Comminution Circuits: Their Operation and Optimization. JKMRC Monograph Series in Mining and Mineral Processing., Brisbane, 1996.
•  Nomura  S.,  Hosada  K.,  Tanada  T., An analysis of selection function for mills using balls as grinding media. Power Technology, 68 (1991) 1–12.
•  O’Sullivan  C., Particulate discrete element modelling: a geomechanics perspective. Spon Press, v. 4, 2011.
•  Pauw  O.G.,  Maré  M.S., The determination of optimum impact-breakage routes for an ore, Powder Technology, 54 (1988) 3–13.
•  Potyondy  D.O.,  Cundall  P.A., A bonded-particle model for rock, International Journal of Rock Mechanics and Mining Sciences, 41 (2004) 1329–1364.
•  Powell  M.S.,  Govender  I.,  McBride  A.T., Applying DEM outputs to the unified comminution model, Minerals Engineering, 21 (2008) 744–750.
•  Powell  M.S.,  McBride  A.T., What is required for DEM simulations to model breakage in mills? Minerals Engineering, 19 (2006) 1013–1021.
•  Powell  M.S.,  Weerasekara  N.S.,  Cole  S.,  LaRoche  R.D.,  Favier  J., DEM modeling of liner evolution and its influence on grinding rate in ball mills, Minerals Engineering, 24 (2011) 341–351.
•  Quist  J.,  Evertsson  C.M., Cone crusher modelling and simulation using DEM, Minerals Engineering, 85 (2016) 92–105.
•  Rajamani  R.K.,  Agrawala  S.,  Mishra  B.K., Mill scaleup: ball collision frequency and collision energy density in laboratory and plant-scale mills, Proceedings, 18th International Mineral Processing Congress, Sydney, 1993, pp. 103–107.
•  Ribas  L.,  Cordeiro  G.C.,  Toledo Filho  R.D.,  Tavares  L.M. Measuring the strength of irregularly-shaped fine particles in a microcompression tester, Minerals Engineering, 65 (2014) 149–155.
•  Rodriguez  V.A., Validation of the UFRJ mechanistic ball mill model, M.S. Thesis, Universidade Federal do Rio de Janeiro, 2016 (in Portuguese).
•  Rowland  C.A.,  Kjos  D.M., Rod and ball mills, in:  Mular  A.L.,  Bhappu  R.B. (Eds.) Mineral Processing Plant Design, AIME, 1980, pp. 239–278.
•  Rozenblat  Y.,  Grant  E.,  Levy Kalman  H.,  Tomas  J., Selection and breakage functions of particles under impact loads, Chemical Engineering Science, 71 (2012) 56–66.
•  Schönert  K., Aspects of physics of breakage relevant to comminution, Proceedings of the 4th Tewksbury Symposium, Melbourne, 1979, pp. 3.1–3.9.
•  Tavares  L.M., Energy absorbed in breakage of single particles in drop weight testing, Minerals Engineering, 12 (1999) 43–50.
•  Tavares  L.M., Optimum routes for particle breakage by impact, Powder Technology, 142 (2004) 81–91.
•  Tavares  L.M., Breakage of single particles: quasi-static, in:  Salman  A.D.,  Ghadiri  M.,  Hounslow  M.J. (Eds.), Handbook of Particle Breakage, Elsevier, 2007, v. 12, pp. 3–68.
•  Tavares  L.M., Analysis of particle fracture by repeated loading as damage accumulation, Powder Technology, 190 (2009) 327–339.
•  Tavares  L.M.,  Carvalho  R.M., Modeling breakage rates of coarse particles in ball mills, Minerals Engineering, 22 (2009) 650–659.
•  Tavares  L.M.,  King  R.P., Single-particle fracture under impact loading, International Journal of Mineral Processing, 54 (1998) 1–28.
•  Tavares  L.M.,  King  R.P., Modeling particle breakage by repeated impacts using continuum damage mechanics, Powder Technology, 123 (2002) 138–146.
•  Tavares  L.M.,  Neves  P.B., Microstructure of quarry rocks and relationships to particle breakage and crushing, International Journal of Mineral Processing, 87 (2008) 28–41.
•  Tuzcu  E.T.,  Rajamani  R.K., Modeling breakage rates in mills with impact energy spectra and ultra fast load cell data, Minerals Engineering, 24 (2011) 252–260.
•  Venugopal  R.,  Rajamani  R.K, 3D simulation of media motion in tumbling mills by the discrete element method, Powder Technology (2001) 157–166.
•  Vogel  L.,  Peukert  W., Determination of material properties relevant to grinding by practicable labscale milling tests, International Journal of Mineral Processing, 74S (2004) S329–338.
•  Von Rittinger  P.R., Lehrbuch der Aufbereitungs Kunde, Ernst and Korn, Berlin, 1867.
•  Wang  M.H.,  Yang  R.Y.,  Yu  A.B., DEM investigation of energy distribution and particle breakage in tumbling ball mills, Powder Technology, 223 (2012) 83–91.
•  Weerasekara  N.S.,  Powell  M.S.,  Cleary  P.S.,  Tavares  L.M.,  Evertsson  M.,  Morrison  R.D.,  Quist  J.,  Carvalho  R.M., The contribution of DEM to the science of comminution, Powder Technology, 248 (2013) 3–24.
•  Weichert  R., Application of defect statistics and fracture mechanics for describing comminution processes, Zement-Kalk-Gips 45 (1992), 51–57.
•  Yahyei  M.,  Weerasekara  N.S.,  Powell  M.S., Characterization of superficial breakage using multi-size pilot mills, Minerals Engineering, 81 (2015) 71–78.
•  Yashima  S.,  Hashimoto  H.,  Kanda  Y.,  Sano  S., Measurement of kinetic energy of grinding media in a tumbling ball mill. Proceedings of the 16th International Mineral Processing Congress, Stockholm, 1988, pp. 299–309.